Fórum: "ujjgyakorlatok"

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Szeretnél hozzászólni? Jelentkezz be.

[278] lorantfy	2005-07-11 12:08:37
70. feladat: Valaki azt állítja, hogy jövő évben (2006) ő és gyermeke is annyi ídős lesz mint születési évszámuk számjegyeinek összege. Igaza lehet?

[277] lorantfy

2005-04-16 13:54:05

Kedves Suhanc és Fórumosok!

Bizonyítottnak kell tekintenek a gondolatátvitellel való információátadás lehetőségét :-), ugyanis az előző hozzászólásom végére odagondoltam, hogy akkor gyártsatok hasonló feladatokat.

Ezen kívül gratula az 55. feladat megoldásaiért! Nagyon tetszettek.

Előzmény: [276] Suhanc, 2005-04-16 12:21:11

[276] Suhanc

2005-04-16 12:21:11

69.Feladat Bizonyítsd be, hogy:

17|3³ⁿ⁺¹5²ⁿ⁺¹+2⁵ⁿ⁺¹11ⁿ

[275] lorantfy

2005-04-15 07:50:54

Kedves Csimbi!

Kösz az ügyes és gyors megoldást. Végülis az a lényeg, hogy ha két szám azonos maradékot ad, k-val osztva, akkor n-edik hatványuk is azonos maradékot ad.

Előzmény: [270] Csimby, 2005-04-13 16:48:53

[274] Suhanc

2005-04-14 20:56:45

Kedves Sirpi és Fálesz Mihály!

Köszönöm a megoldásotokat! Igazából már lemondtam róla, hogy bárkit is érdekeljen a feladat... Sirpi, említettél egy közepes megoldást, ami szerintem megegyezik az én megoldásommal. Mindenesetre akkor én azt engedelmeddel "pofátlanul beírnám", szerintem van üzenete...

Megfelelő módon osztjuk részekre a baloldalon lévő mennyiségeket, és ezekből fogjuk a jobb oldal tagjait a számtani- mértani közepek közötti egyenlőtlenség egítségével becsülni.

Eredetileg: a³b+b³c+c³a $\ge$ a²bc+ab²c+abc²

Ekkor:

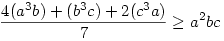
$\frac{4(a^3b)+(b^3c)+2(c^3a)}{7} \ge a^2bc$

$\frac{2(a^3b)+4(b^3c)+(c^3a)}{7} \ge ab^2c$

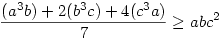
$\frac{(a^3b)+2(b^3c)+4(c^3a)}{7} \ge abc^2$

E három egyenlőtlenséget összeadva épp a bizonyítandó állítást kapjuk...

Előzmény: [273] Sirpi, 2005-04-14 14:24:06

[273] Sirpi

2005-04-14 14:24:06

Hát igen, ez jóval egyszerűbb megoldás. Viszont igaz, hogy a másik hosszú, meg számolós, de az enyém :-) Közben rájöttem én is egy másik, nem ennyire számolós megoldásra.

Osszuk le mindkét oldalt abc-vel (ha valamelyik szám 0, akkor triviálisan igaz az egyenlőtlenség):

a²/c+b²/a+c²/b $\geq$ a+b+c

Átrendezve:

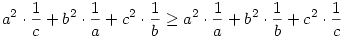
$a^2 \cdot \frac1c + b^2 \cdot \frac1a + c^2 \cdot \frac1b \geq a^2 \cdot \frac1a + b^2 \cdot \frac1b + c^2 \cdot \frac1c$

Mindkét oldalon az a²,b²,c² számok vannak páronként összeszorozva az 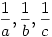$\frac1a, \frac1b, \frac1c$ számokkal, és össze vannak adva a szorzatok, csak más sorrendben vannak összepárosítva a két oldalon. Ismert tétel (rendezési tételnek, vagy Szűcs Adolf-tételnek is hívják), hogy egy ilyen szorzat akkor lesz maximális, ha a két összeszorzandó sorozat azonos módon van rendezve, akkor lesz a legkisebb, ha ellentétes módon, ebből következően az összes többi permutáció e kettő közt fog elhelyezkedni.

A jobb oldalon fordított sorrendben van rendezve a két számhármas (ha pl. a² $\geq$ b² $\geq$ c², akkor 1/a $\leq$ 1/b $\leq$ 1/c), így a bal oldal legalább akkora, mint a jobb.

[272] Fálesz Mihály

2005-04-14 14:03:12

Szia Sirpi,

A megoldást ismertem, ezért nem írtam le eddig. (A 83-as párizsi diákolimpián a legnehezebb feladatot, amire a teljes magyar csapat összesen 1 pontot szerzett, erre az egyenlőtlenségre lehetett visszavezetni egy kis trükkel.)

(a³b+b³c+c³a)-(a²bc+ab²c+abc²)=

=ab(a-c)²+bc(b-a)²+ca(c-b)² $\ge$ 0.

F.M. :-)

Előzmény: [271] Sirpi, 2005-04-14 11:16:40

[271] Sirpi

2005-04-14 11:16:40

Na, akkor a rég eltemetett 55. feladatról írnék, ami úgy szólt, hogy ha a,b,c $\geq$ 0, akkor a³b+b³c+c³a $\geq$ a²bc+ab²c+abc².

Kijött közepekkel is, de ha nem akarok nagyágyúkat használni, akkor ki lehet direkt módon is hozni. Első észrevétel, hogy ha a=b=c=0, akkor triviálisan igaz az állítás. Ha meg nem, akkor szorozzunk fel (a+b+c)-vel:

(a+b+c)(a³b+b³c+c³a) $\geq$ abc(a+b+c)²

Elvégezve a beszorzást mindkét oldalon 9-9 tagot kapunk, amiből 3 egyezik:

a⁴b+ab³c+a²c³+a³b²+b⁴c+abc³+a³bc+b³c²+ac⁴ $\geq$ a³bc+ab³c+abc³+2a²b²c+2a²bc²+2ab²c²

Rendezve:

(a⁴b+b³c²-2a²b²c)+(b⁴c+c³a²-2ab²c²)+(c⁴a+a³b²-2a²bc²) $\geq$ 0

Ez pedig nyilvánvalóan igaz, mert ez átírható a következő alakra:

b(a²-bc)²+c(b²-ac)²+a(c²-ab)² $\geq$ 0

Egyenlőség akkor áll fenn, ha minden tag 0. Minden tag egy szorzat, ezért az egyenlőségnek az a feltétele, hogy minden tényező valamelyik tagja 0. Nézzük meg az eredeti egyenletet abban az esetben, ha pl. c=0, ekkor a bizony1tandó egyenlet az a³b $\geq$ 0 alakra egyszerűsödik. Vagyis ha van nulla a számok közt, akkor egyenlőség áll fenn, amennyiben van köztük még legalább egy másik nulla is.

Ha nincs nulla a számok közt, akkor pedig az a²=bc,b²=ac,c²=ab egyenlőségek mindegyikének kell teljesülnie, de ha feltesszük, hogy c a legnagyobb, és c²=ab, abból rögtön következik, hogy a=b=c. Tehát az (a,a,a) és az (a,0,0) számpárok esetén van egyenlőség.

Előzmény: [189] Suhanc, 2004-09-22 20:12:09

[270] Csimby

2005-04-13 16:48:53

2^6n-1+5ⁿ^.3²ⁿ⁺² akkor és csak akkor osztható 19-cel, ha a 2-szerese is osztható vele, tehát vizsgáljuk a 2-szeresét: 2⁶ⁿ+2^.5ⁿ^.3²ⁿ⁺²=64ⁿ+2^.5ⁿ^.9^.9ⁿ

2^.9 $\equiv$ -1 (mod 19) $\implies$ 64ⁿ+2^.5ⁿ^.9^.9ⁿ $\equiv$ 64ⁿ-45ⁿ

64ⁿ-45ⁿ=(64-45)(64^n-1+64^n-2^.45+64^n-3^.45²+...+64^.45^n-2+45^n-1)

64-45=19, tehát készen vagyunk.

Előzmény: [269] lorantfy, 2005-04-13 09:25:54

[269] lorantfy	2005-04-13 09:25:54
68. feladat: Bbh. minden n-re 19 osztója 2^6n-1+5ⁿ^.3²ⁿ⁺²-nek !

[268] Lóczi Lajos	2005-03-29 22:26:50
Aki a (határozatlan) integrálokkal szeretne egy kicsit játszani (és éppen nincs szimbolikus programcsomagja kéznél), azoknak ajánlom a http://integrals.wolfram.com/ címet. Ott meglátod a kérdésedre az általános választ, ami speciális függvényt tartalmaz. (Ezekről egy hatalmas gyűjtemény l. pl. a http://functions.wolfram.com/ címen.) Persze minden konkrét k-ra és n-re az integrál elemien kiszámítható. DE, a paraméterekkel csínján kell azért bánni, hiszen itt ugye hallgatólagosan azt FELTÉTELEZTÜK, hogy k és n pl. pozitív egészek. De már a k=1 és n=-1 esetben is teljesen más alakú lesz a primitív függvény, mint amit írtál. (Sőt, ugye még ott vannak az a és b paraméterek is...nulla vagy nem nulla, stb.)
Előzmény: [266] tudniakarok, 2005-03-27 11:58:50

[267] lorantfy	2005-03-27 12:03:23
Na ez rendben van! Hát ebből látszik, hogy ha be van szorozva a belső fgv. deriváltjának megfelelő x hatvánnyal akkor könnyű a dolgunk. Ebből azt is lehet sejteni, miért nehéz, ha nincs beszorozva a deriválttal.
Előzmény: [264] tudniakarok, 2005-03-27 00:50:32

[266] tudniakarok	2005-03-27 11:58:50
lemaradt hogy x a változó,ahogy eddig is

[265] tudniakarok

2005-03-27 11:50:57

Azaz,ez is általánosan:

$\int x^{k-1}(ax^k+b)^n=\bigg[\frac{(ax^k+b)^{n+1}}{(n+1)ka}\bigg]$

[264] tudniakarok

2005-03-27 00:50:32

Kicsi a világ,főleg a neten!:) Bár szégyen szemre nekem nem ugrik be az ismerettség,de elég meggyőző a sporttárs megszólítás,úgyhogy biztos ismerjük egymást,csak rossz az arcmemóriám!bocsánat. A feladatot eddig könnyebb megoldani mint beírni szépen:)

$\int x\big(ax^2+b)^n dx=\bigg[\frac{(ax^2+b)^{n+1}}{(n+1)2a}\bigg]$

Előzmény: [263] lorantfy, 2005-03-26 22:30:21

[263] lorantfy

2005-03-26 22:30:21

Kedves Sporttárs!

Most jöttem rá, hogy ismerlek valahonnan... Próbálkozz ezzel:

Legyen egyenlőre k=2 és szorozzuk be egy x-szel, hogy könnyebb legyen:

$\int{x\cdot(ax^2+b)^n}dx$

Előzmény: [262] tudniakarok, 2005-03-26 18:21:25

[262] tudniakarok	2005-03-26 18:21:25
Köszönöm a megerősítést!(a nagy könyvben nem találtam meg:) Gondoltam hogy a kérdésem belebonyolódik a matamatika olyan részeibe, ami egyelőre távol áll az én tudásomtól! Na de mind1!
Előzmény: [261] lorantfy, 2005-03-26 01:09:14

[261] lorantfy

2005-03-26 01:09:14

Ez jól van így. Majdnem olyan, mint ahogy a nagykönyvekben meg van írva. Még egy +C-t szoktak hozzáírni, minthogy ez határozatlan integrál, szóval egy konstans erejéig határozatlan. Ha visszaderiválsz a konstans eltűnik, így bármi lehet.

Arra a kérdésre, mi van, ha a kerek zárójelen belül (ax^k+b)-van, a válasz: baj. Ettől kicsit elbonyolódik a dolog.

Előzmény: [260] tudniakarok, 2005-03-25 23:12:48

[260] tudniakarok

2005-03-25 23:12:48

Kérlek segítsetek! Házi volt a csonkakúp térfogatának bizonyítása integrálszámítással,na most én lusta voltam bontogatni a zárójeleket,így összetett fv. primitív fv.-ét kerestem,kijött a jó képlet,a tanárom szerint lehet hogy csak véletlen,mert hogy ő nem érti(vagy csak nem akarja gyötörni magát)! Na de a lényeg,tehát vmi ilyesmi jött ki általánosan:

$\int{(ax+b)^n}dx=\bigg[\frac1a\frac{(ax+b)^{n+1}}{n+1}\bigg]$ szerintem jó,de ha találtok vmi hibát lécci közöljétek,mert még nem csináltam túl sok ilyen példát!Előre is köszi! Ja és még egy kérdés: mi van akkor ha az intergrandusban a változó nem elsőn hanem k-adikon van,erre még nem jöttem rá!?

[259] jonas	2005-03-23 23:34:22
Ez ötletes megoldás. Ráadásul ez akkor is működik, ha megengedünk 64-nél több egyest.
Előzmény: [258] Káli gúla, 2005-03-23 22:44:16

[258] Káli gúla	2005-03-23 22:44:16
Tegyük fel, hogy a sztringnek csak a "10"-zel kezdődő 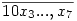$\overline{1 0 x_3 . . . , x_7}$ hétjegyű számokat kell tartalmaznia legalább egyszer. Rendezzük ezeket növekvő sorrendbe. A 32 db második helyiértékes 0 különböző helyre fog kerülni a sztringben, mert a mögöttük álló 5 bites számok különbözők. Az első 16 szám harmadik helyiértékes nullája is mind különböző lesz, mert a mögöttük álló 4 bites számok különbözők, ugyanígy az első 8 negyedik, az első 4 ötödik, az első 2 hatodik, az első 1 hetedik helyiértékes 0 is mind más. (Különböző helyiértékű 0-k is különbözők, mert balra különböző számú 0 valasztja el a kezdő 1-estől.) Ez összesen 32+16+...+1=63 darab nulla, tehát nincs 127-nél rövidebb sztring.
Előzmény: [253] jonas, 2005-03-21 22:07:57

[257] jonas	2005-03-22 19:33:57
Hadd folytassam a tegnapi gondolatomat. Mar megallapitottuk, hogy ha pontosan 64 egyessel sikerul a feladat, akkor minden egyessel kezdodo 7-jegyu szam pontosan egyszer szerepel. Ez azt jelenti, hogy ha egy ilyen bitsorozatot abrazolunk a grafon, akkor a kapott vonalban minden olyan el pontosan egyszer szerepel, ami egy olyan csucsbol indul, ami 1-essel kezdodik. Sporolni csak azokon az eleken lehetne, amik a 0-assal kezdodo elekbol indulnak. Ezek az elek azonban az egyetlen (000000,000000) elen kivul fat alkotnak, ezert nem lehet elhagyni beloluk azon a bizonyos egy elen kivul. Ha ugyanis az egesz grafbol kivonjuk a vonalat, akkor csak a fa elei maradhatnak meg (de azok elvileg akarmilyen elojellel, hiszen lehetne, hogy egy 0-val indulo elen tobbszor megyunk at), de egy fan ez csak ugy lehetseges, ha minden el 0-szor van benne. Tehat legalabb 63 nullasra valoban szukseg van. (Ezt ennel biztos egyszerubben is be lehet latni.) Meg egy megjegyzes. A grafos megkozelitesbol lehet sejteni, hogy valojaban nagyon sok ilyen de Bruijn kor van. Ez tenyleg igy igaz: a A016031 sorozat megadja ezek szamat. Ebbol az is kovetkezik, hogy nagyon konnyu de Bruijn kort eloallitani: egyszeruen ki kell indulni a 0000000 sorozatbol, es utana irni veletlen biteket arra vigyazva, hogy ne vegyuk egyik 7 bites szamot sem tobbszor. Ekkor persze elofordulhat, hogy levagjuk a graf egy reszet, ezert nem tudjuk befejezni a kort, de ilyenkor egyszeruen ujra probalkozhatunk, es hamar sikerulni fog. Az elobb ezzel az egyszeru veletlen modszerrel allitottam elo a szamokat. Itt van a kod, ha valakit erdekel.

Előzmény: [256] lorantfy, 2005-03-22 14:51:19

[256] lorantfy	2005-03-22 14:51:19
Kedves Jónás! Nagyon szép a bizonyítás! Igazi "vezérlő dinamika". De nézzük meg mit is láttunk be ezzel. n=7 esetén a számjegyek 6 jegyűek és 2⁶=64 db van belőlük, tehát a gráfnak 128 éle van. Indulunk az egyik csúcsból és bejárjuk az Euler kört. Az első szám 6 jegyű és minden élen való áthaladás egyel növeli a szám hosszát. Tehát 6+2*64=134 jegyű számot állítottunk elő, mely tartalmazza az összes 7 hosszúságú bitsorozatot, de 67 db 1-es számjegyet tartalmaz. Példa képpen mutatom az n=4 jegyű esetet.

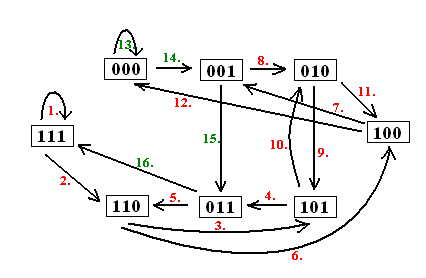Előzmény: [255] jonas, 2005-03-21 22:57:58

[255] jonas

2005-03-21 22:57:58

Akkor lelövöm a "vezérlő dinamikát". Nem akartam rögtön elmondani, mert ismertem (Simonyi tanár úr gyakorlatán volt feladat); hadd gondolkodjanak a "fiatalok". Azt viszont nem tudom megmondani, hogy kevesebb nullával le lehet-e írni az 1000000...1111111 számokat. (Azért elgondolkozom még rajta, most hogy a bizonyítást átgondoltam, lehet, hogy könnyű lesz.) Ha viszont megengedünk 64-nél több egyest, akkor azt hiszem hogy összesen 127-nél kevesebb számjeggyel is le lehet írni őket, de nem tudom, hány számjegy kell.

Aki tehát gondolkozni akar a 64 számjegy bizonyításán, az ne olvasson tovább.

Azt fogom belátni, hogy bármely n-re létezik ún de Bruijn-ciklus, vagyis hogy fel lehet írni egy kört 2ⁿ bitből úgy, hogy a körből n szomszédos bitet összeolvasva minden n hosszú bitsorozatot pontosan egyszer kapunk meg. Ha már tudjuk, hogy van n=7-re de Bruijn-ciklus, akkor ezt felvágva a 0000000 előfordulásának utolsó számjegyénél, egy megfelelő 127 hosszú bitsorozatot kapunk. (Azt könnyű látni, hogy pontosan 64 egyes van benne.)

Ehhez pedig vegyünk egy irányított gráfot, amelynek csúcsai az n-1 hosszú bitsorozatok, az (u,v) pedig akkor és csak akkor él, ha u utolsó n-2 bitje megegyezik v első n-2 bitjével. Ebben a gráfban van Euler-kör, mert összefüggő, és minden csúcsának megegyezik a ki- és a befoka, ugyanis mindkettő 2. Ha nézzük a gráf egy (u,v) élét, ezt jellemezhetjük egy n bites számmal, amit úgy kapunk, hogy u és v bitjeit egymásra helyezzük úgy, hogy fedjék egymást. Két szomszédos élhez két olyan szám tartozik, hogy az első él utolsó n-1 bitje éppen a második él első n bitje, ez tudniillik a közös csúcs. Ebből következik, hogy egy Euler-kör éppen egy de Bruijn körnek felel meg.

(A Konkrét Matematika egyébként egy helyen megemlíti a de Bruijn köröket, noha ahhoz a bizonyításhoz, ahol használja, valójában nincs szükség rájuk. Bizonyítást nem ad a körök létezésére, csak hivatkozik a Programozás Művészetére.)

Előzmény: [254] lorantfy, 2005-03-21 22:27:17

[254] lorantfy

2005-03-21 22:27:17

Kedves Jónás és Levi!

Örülök, hogy "rákattantatok" a problémára! Bevallom nektek, hogy én is csak n=4-jegyűig írtam fel, mint Levi és ebből gondoltam, hogy nagyobb n-ekre is igaz.

Külön gratula Jónásnak, hogy volt türelme hozzá!

Bár ez már nem ujjgyakorlat, de jó lenne, ha valaki rámutatna a "vezérlő dinamikára", szóval, hogy miért lehet ezt minden n-re megtenni!

Jó kérdés a 0-k számának csökkentése is!

Előzmény: [253] jonas, 2005-03-21 22:07:57

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Már regisztráltál?
Új vendég vagy?