|
| [777] koma | 2012-10-13 17:12:00 |
 ténylegesen elírtam,elnézést
|
|
|
|
| [774] Lapis Máté Sámuel | 2012-10-13 11:13:11 |
 1,Igazoljuk, hogy x>1 esetén:
log2x+logx2 2 2
Miután megvannak indokolva a kikötések vezess be új alapot.

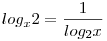
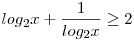
Új ismeretlen a=log2x
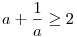
Mivel x>1,egy pozitív szám és reciprokának összege nagyobb egyenlő kettő!
|
| Előzmény: [773] koma, 2012-10-13 10:48:04 |
|
| [773] koma | 2012-10-13 10:48:04 |
 Köszönöm szépen a válaszokat! Az utóbbi időben találtam néhány egyenlőtlenséget, amiket nem tudtam megoldani, ha valaki tudna segíteni annak nagyon örülnék.
1,Igazoljuk, hogy x>1 esetén:
log2x+logx2 2 2
2,Igazoljuk, hogy n 2 esetén: 2 esetén:
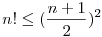
|
|
|
|
|
| [769] koma | 2012-10-01 18:50:09 |
 Kongruenciák! segítségével bizonyítsuk be,hogy:
133 osztója 11n+2 + 122n+1
Minden segítséget köszönök előre!
|
|
| [768] Hajba Károly | 2012-09-22 23:18:44 |
 Igen.
S működik ez bármely C > [A, B] esetén is, csak ekkor a helyiértékekre nem jön ki ilyen szépen csak tízhatvány esetén.
A * B = ? . => . (A+B-C)*C + (C-A)*(C-B)
C-A . C-B . | . C-X = A+B-C
(C-A)+(C-B)= 2C-(A+B) => X
(C-A)*(C-B)
|
| Előzmény: [767] polarka, 2012-09-22 22:35:55 |
|
| [767] polarka | 2012-09-22 22:35:55 |
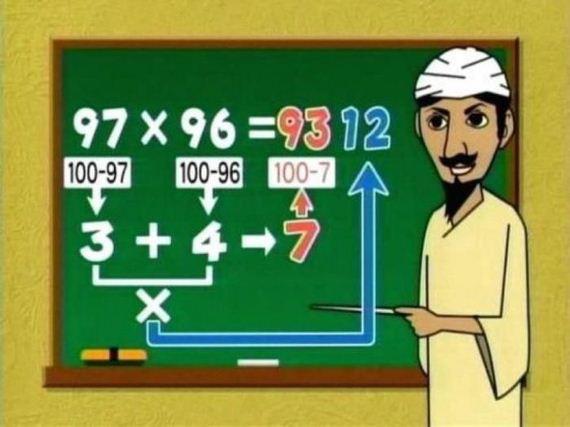
 egy a számtalan fejszámolási trükkök közül. 100-nál kisebb számokra működik, de kiterjeszthető nagyobb számokra is.
Ugye a számolási eljárás a következőt állítja: (10a+b)*(10c+d)=(100-(100-(10a+b)+100-(10c+d)))*100+(100-(10a+b))*(100-(10c+d)) ahol a,b,c,d = 0;1;2;...;9
Amiből a zárójelek felbontása után belátható, h megegyeznek. Tehát az eljárás a megfelelő értelmezés mellett működik 2jegyű számokra. De olyan számoknál érdemes használni, amelyek közel vannak a 100-hoz.
Mondjuk sztem a szokásos módszerrel sem sokkal nehezebb számolni: 97*96=97*(100-4)=9700-4*(100-3)=9300+4*3=9312
|
| Előzmény: [766] Hajba Károly, 2012-09-22 15:29:49 |
|
| [766] Hajba Károly | 2012-09-22 15:29:49 |
 Ez működik más számokkal is? S ha igen, miért?
:o)
|
 |
|
| [765] lorantfy | 2012-08-26 21:17:35 |
 USA versenyfeladat volt. Az orosz Duma-ra volt kiírva, aztán átfogalmazva javasoltam is B-be, persze nem a magyar parlamentre igazítva.
Tegyük fel, hogy az orosz parlamentnek 1000 tagja van és minden tag ad egy pofont pontosan egy másik tagnak. Bizonyítsuk be, hogy egy képviselő alakíthat a parlamentben egy olyan 334 tagú bizottságot amelynek egyik tagja sem adott pofont egy másik tagnak! (USA, Matematikai Tehetségkutató Verseny)
Egy internetes klubnak pontosan 1000 tagja van. Tegyük fel, hogy minden tag küld egy e-mailt pontosan egy másik tagnak. Bizonyítsuk be, hogy a tagok közül kiválaszthatunk egy olyan 334 tagú csoportot, amelynek egyik tagja sem küldött e-mailt egy másik tagnak!
|
| Előzmény: [763] Róbert Gida, 2012-08-25 13:40:18 |
|
|
| [763] Róbert Gida | 2012-08-25 13:40:18 |
 A 386 fős Parlamentben mindenki pontosan 1 képviselőtársát pofozta fel. Bizonyítsuk be, hogy fel lehet állítani egy 129 fős bizottságot úgy, hogy tagjai közül senki sem pofozott fel másik tagot! Továbbá lássuk be, hogy a korlát éles, azaz 130 fős ilyen bizottság nem mindig létezik.
|
|
| [762] juantheron | 2012-07-24 11:35:28 |
 If x3(x+1)=(x+k)(x+2k) and 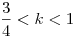 , ,
Then Find
(i) Number of Real Roots.
(ii) Greatest Real Root.
(iii) Least Real Root.
|
|
|
|
|
|
|
| [756] N.Hai | 2012-06-10 23:56:29 |
 Adott egy sakktábla, melynek bal alsó sarkában (A1) egy bábú áll. Ez a bábú a következőképpen mozoghat. Vagy egyet lép felfele, vagy egyet lép jobbra, vagy egyet lép átlósan a jobb felső sarokba (tehát úgy lép, mint egy király, ami folyamatosan a jobb felső sarokba tart). A király a mozgása során valamilyen úton az A1-ből a H8-ba kerül. Tegyük fel, hogy felsoroltuk az összes utat, és véletlenszerűen választunk egy útvonalat. (Tehát minden útvonal választásának az esélye ugyanakkora, függetlenül az út hosszától.) Mennyi az esélye annak, hogy egy olyan utat választottunk, amely érinti az F5 mezőt?
A feladat megoldása előtt megkérnélek titeket arra, hogy becsüljétek meg az intuíciótok alapján, hogy mekkora lehet ez a szám.
|
|
| [755] Lóczi Lajos | 2012-06-09 21:48:27 |
 Egy számolás során bukkant fel az alábbi kifejezés, amely kicsit megfeküdte a gyomromat: természetesen az a cél, hogy minél egyszerűbb alakban írjuk fel. (Arra jutottam, hogy a végeredmény leírható 2 elemi művelettel és két egész számmal.)
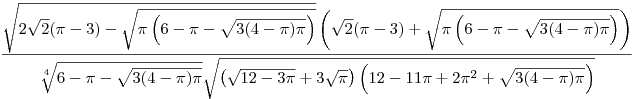
|
|
|





 2
2 
 121*11n+12*11n=133*11n
121*11n+12*11n=133*11n



 0.35, ami jóval kevesebb, mint amit én becsültem.
0.35, ami jóval kevesebb, mint amit én becsültem. 

