|
| [727] juantheron | 2012-05-18 17:02:03 |
 Thanks Sakkmath i have got my solution after seeing your Answer
bcz I have solve a simillar Problem Yesterday where I have calculate value of sin (10).sin (20).sin (30)......sin (890)
Now I have another doubt in my min
can we calculate the value of
cot (10).cot (20).cot (30)........cot (440)=
|
|
| [726] juantheron | 2012-05-18 16:58:09 |
 Let A=cos (10).cos (20).cos (30).........cos (890)
Now using cos (90-a)=sin (a)
So A=sin (10).sin (20).sin (30).........sin (890)
and Let B=sin (20).sin (40).sin (60).........sin (880)
Now AB=(sin (10).sin (890)).(sin (20).sin (880)).........(sin (440).sin (460)).sin (450)
So AB=(sin (10).cos (10)).(sin (20).cos (20)).........(sin (440).cos (440)).sin (450)
So 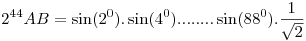
So 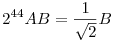
So 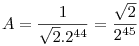
bcz B 0 0
|
|
| [725] juantheron | 2012-05-18 16:57:24 |
 Thanks sakkmath after seeing your answer I have got a method
bcz i have solve a simillar problem Yesterday where i have
calculate the value of
sin (10).sin (20).sin (30).........sin (890)
My solution::
Let A=cos (10).cos (20).cos (30).........cos (890)
Now using cos (90-a)=sin (a)
So A=sin (10).sin (20).sin (30).........sin (890)
and Let B=sin (20).sin (40).sin (60).........sin (880)
Now AB=(sin (10).sin (890)).(sin (20).sin (880)).........(sin (440).sin (460)).sin (450)
So AB=(sin (10).cos (10)).(sin (20).cos (20)).........(sin (440).cos (440)).sin (450)
So 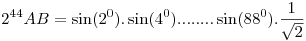
So 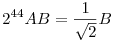
So 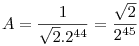
bcz B 0 0
|
|
|
| [723] juantheron | 2012-05-18 07:06:44 |
 Thanks friends got it.
New task::
Numerical value of cos (10).cos (30).cos (50).......cos (890)=
where all angle are in Degree
|
|
| [722] m2mm | 2012-05-17 21:16:33 |
 We may assume that x y. Then (y+2)2=y2+4y+4>y2+3x>y2. So, if y2+3x is a square, it must be (y+1)2. Then y2+2y+1=y2+3x, so 2y+1=3x, which means that 2y y. Then (y+2)2=y2+4y+4>y2+3x>y2. So, if y2+3x is a square, it must be (y+1)2. Then y2+2y+1=y2+3x, so 2y+1=3x, which means that 2y -1 (mod 3), so y -1 (mod 3), so y 1 (mod 3). Hence, y=3k+1 for some positive integer k. Since 2y+1=3x, then 6k+3=3x, 2k+1=x. 1 (mod 3). Hence, y=3k+1 for some positive integer k. Since 2y+1=3x, then 6k+3=3x, 2k+1=x.
As x2+3y is a square, then (2k+1)2+3(3k+1)=4k2+4k+1+9k+3=4k2+13k+4 as well.
But (2k+2)2=4k2+8k+4 4k2+13k+4<4k2+16k+16=(2k+4)2, so 4k2+13k+4=(2k+2)2=4k2+8k+4, or 4k2+13k+4=(2k+3)2. 4k2+13k+4<4k2+16k+16=(2k+4)2, so 4k2+13k+4=(2k+2)2=4k2+8k+4, or 4k2+13k+4=(2k+3)2.
If 4k2+13k+4=4k2+8k+4, then k=0, x=y=1 (and this pair is a soultion).
If 4k2+13k+4=(2k+3)2, then 4k2+13k+4=4k2+12k+9, so k=5. Then the solution is (11,16) or (16,11).
|
| Előzmény: [717] juantheron, 2012-05-16 20:17:02 |
|
|
|
| [719] juantheron | 2012-05-17 08:49:02 |
 Thanks Nadorp got it
task:: find positive Integer value of x and y for which x2+3y and y2+3x is an perfect square
My solution::
Let x2+3y=l2 and y2+3x=m2
Where l,m Z Z
Then (x2-y2)-3(x-y)=l2-m2
(x-y).(x+y-3)=(l+m).(l-m)
means either x+y-3=l+m and x-y=l-m
2x=3+2l or 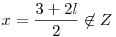
similarly 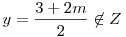
but when i put rendomly put values like (1,1) and (11,16) and (16,11)
but how can i calculate it
Thanks
|
|
|
| [717] juantheron | 2012-05-16 20:17:02 |
 Nwe task::
The number of ordered pairs of positive integers x,y such that x2+3y and y2+3x are both perfect squares
|
|
| [716] juantheron | 2012-05-16 19:46:00 |
 Yes Friends your answer is Right
I have solved like that way
x2=4+[x]
here R.H.S(right hand side) is an Integer that means L.H.S(Left hand side must be an Integer)
So x2 Z Z
So Let x2=k, where k>0
So 
So our equation convert into ![k=4+[\pm \sqrt{k}]](keplet.cgi?k=35D7CCA2B1205F53)
Now after checking certain value of k like k=1,2,3,4,5,6
We Get only k=2 and k=6 satisfy the given equation
and after k 7, we get L.H.S # R.H.S 7, we get L.H.S # R.H.S
But Not sure about k 7 has no value for which satisfy the given equation 7 has no value for which satisfy the given equation
can anyone clear last line explanation
Thanks
|
|
| [715] juantheron | 2012-05-16 19:35:38 |
 Thanks Nadorp and Small Potato
for Integration I have solve it after yours work
I have solved it like in that way
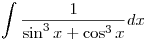
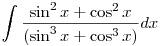
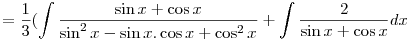
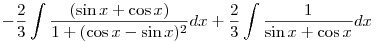
Put (cos x-sin x)=tand (sin x+cos x)dx=-dt
and 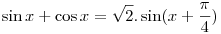
after that we can calculate easily
|
|
|
|
|
|
| [710] nadorp | 2012-05-16 13:00:34 |
 Igazad van, de azért beírom, mert nem nehéz
sin3x+cos3x=(sin x+cos x)(1-sin xcos x)
Végezzük el az integrálban a
cos x-sin x=s helyettesítést
Ekkor 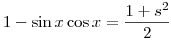 és és
(sin x+cos x)2+(cos x-sin x)2=2 és
-(sin x+cos x)dx=ds miatt
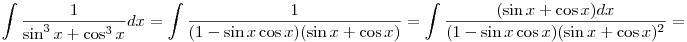
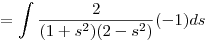
Innen már könnyű...
|
| Előzmény: [709] SmallPotato, 2012-05-16 11:51:16 |
|
|
| [708] logarlécész | 2012-05-16 11:05:44 |
 Ha jól értem, a megoldás kellene.
A legegyszerűbb grafikusan. A felrajzolásból látszik, hogy megoldás lesz a +2; -2 és lesz még egy megoldás -3 és -2 között. Ennek a pontos értékét én sem tudom meghatározni, nagyjából -2,19258, ha nem tévedek.
|
| Előzmény: [707] juantheron, 2012-05-16 10:10:27 |
|
|
|
|
| [704] Lóczi Lajos | 2012-05-15 20:21:56 |
 Fejezzük ki valamelyik változót a másik segítségével az
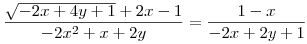
egyenletből.
|
|





 0
0 y. Then (y+2)2=y2+4y+4>y2+3x>y2. So, if y2+3x is a square, it must be (y+1)2. Then y2+2y+1=y2+3x, so 2y+1=3x, which means that 2y
y. Then (y+2)2=y2+4y+4>y2+3x>y2. So, if y2+3x is a square, it must be (y+1)2. Then y2+2y+1=y2+3x, so 2y+1=3x, which means that 2y -1 (mod 3), so y
-1 (mod 3), so y Z
Z  7, we get L.H.S # R.H.S
7, we get L.H.S # R.H.S 

