| [578] Fernando | 2010-02-03 14:35:40 |
 Kedves Jonas!
Köszönöm szépen, ez nem semmi... ettől lehidaltam! Hogy ez eddig nem jutott eszembe... A barátaimmal már mindenre gondoltunk, de ezekre nem... Az általános megoldás valóban vmi durva lehet, meg érdekes lehet a levezetés is.
Erről a két egyszerű megoldásról csak egy Zorán idézet jut eszembe :
"Az életben annyi mindent nem értek, Hogy egyre jobbnak érzem, amit megértek... De bevallom, nem lettem boldogabb, Ha elhittem érthetetlen dolgokat, S az igazság közben mindig olyan egyszerűen szólt" (Zorán: Egészen egyszerű dal)
|
| Előzmény: [574] jonas, 2010-02-03 14:00:58 |
|
| [577] Fernando | 2010-02-03 14:27:02 |
 Kedves Vogel!
Én is ezt hittem először, de nekem nem akart szétválni, akárhogy kalapáltam. :( Persze lehet, hogy másnak szétválik, ha sikerül feltétlenül kíváncsi lennék rá! :)
|
| Előzmény: [575] vogel, 2010-02-03 14:08:39 |
|
| [576] SmallPotato | 2010-02-03 14:10:54 |
 Háááát ... nem számoltam utána, de elég durva:
http://www.wolframalpha.com/input/?i=y%27%28x%29*y%3D2*x%2By%28x%29
(bocsánat, hogy nem direkt a link, de a % jelek bekavarnak.)
|
| Előzmény: [573] Fernando, 2010-02-03 13:26:34 |
|
|
|
| [573] Fernando | 2010-02-03 13:26:34 |
 Sziasztok!
Diffegyenletekből korrepetáltam, amikor a következőre bukkantam:
y'y=2x+y
Ártatlannak tűnt, de gyanúsan mégsem az... Szívesen fogadok ötleteket!
|
|
|
|
|
|
| [568] ebach | 2010-02-02 19:57:50 |
 "Legyen f : N -> N olyan leképezés, hogy tetszőleges n természetes számra(n + 1)f > nf(négyzet). Bizonyítsuk, hogy f identitás."
Minden megoldást szívesen fogadok, kellemes időtöltést mindenkinek. (Egyébként sürgős lenne.) Köszönöm.
|
|
|
|
| [565] HoA | 2009-08-31 08:50:46 |
 Attól tartok, az adott középpontú, adott parabolát érintő kör szerkesztése nem euklideszi feladat, így ennek sugara sem meglepő ha kívül esik a szerkeszthető szakaszok halmazán.
|
| Előzmény: [564] psbalint, 2009-08-29 16:21:43 |
|
| [564] psbalint | 2009-08-29 16:21:43 |
 sziasztok! egy rövid kérdésem lenne. elfelejtettem, hogy hogyan számoljuk ki egy pont és egy parabola távolságát. illetve hát sejtem, hogy melyik egyenesnek kell melyikre merőlegesen állnia, de mindig harmadfokú egyenlet jön ki a végén. segítsééég!
|
|
|
| [562] jonas | 2009-07-15 13:38:40 |
 Kis egészeken próbálgatással azt kapjuk, hogy az a=b=c=2 az egyetlen megoldás. Nagy számokra nem lehet megoldás, mert a faktoriális monoton, így ha valamelyik szám nagy, akkor a d is nagy, de akkor a,b,c d-1 csakhogy ebből a!,b!,c! d-1 csakhogy ebből a!,b!,c! (d-1)!<d!/3 így a!+b!+c!<d! ami ellentmondás. (d-1)!<d!/3 így a!+b!+c!<d! ami ellentmondás.
|
| Előzmény: [561] MTM, 2009-07-15 11:06:14 |
|
| [561] MTM | 2009-07-15 11:06:14 |
 Oldjuk meg a poz. egészek halmazán!
a!+b!+c!=d!
|
|
|
|
| [558] Csimby | 2009-04-07 02:18:32 |
 F(x,y) az (x,y) pont távolságainak összege a (-1,1),(1,-1),(-2,-2) pontoktól. Ismert, hogy ez a három pont által meghatározott háromszög izogonális pontjában minimális, melyet megszerkeszthetünk ha az oldalakra kifelé írt szabályos háromszögek megfelelő csúcsát összekötjök az eredeti háromszög megfelelő csúcsával. Ezek alapján a keresett pont az x=y egyenesen lesz. És mivel az izogonális pontból az oldalak 120° szögben látszanak, azt is könnyű látni, hogy a keresett pont: 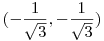 . .
|
| Előzmény: [557] Cogito, 2009-04-05 15:20:06 |
|
| [557] Cogito | 2009-04-05 15:20:06 |
 108.feladat: 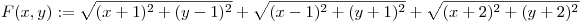 , ahol x és y tetszőleges valós számok. Keressük meg F lehető legkisebb értékét. , ahol x és y tetszőleges valós számok. Keressük meg F lehető legkisebb értékét.
|
|
| [556] MTM | 2008-11-24 21:20:23 |
 Üdv!
Határozzuk meg
a, x4-4x3+1 és x3-3x2+1
b, 3x6-x5-9x4-14x3-11x2-3x-1 és 3x5+8x4+9x3+15x2+10x+9
polinomok legnagyobb közös osztóját.
|
|
|
|










 d-1 csakhogy ebből a!,b!,c!
d-1 csakhogy ebből a!,b!,c!

