| [52] Hajba Károly | 2003-12-22 00:09:49 |
 Kedves László!
Vártam néhány napot, hátha valaki lecsap rá, így hát én adok a 15. feladatra megoldást.
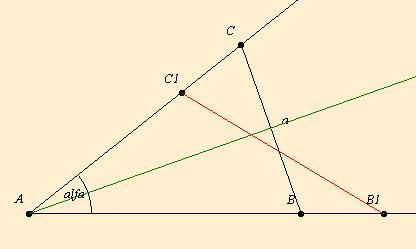
A párhuzamos szelők miatt a B1E és C1D egyenesek éppen a CB szakaszfelező A1 pontban metszik egymást. Ebből következik, hogy A1B1C1 háromszög területe 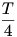 . Hasonló megfontolásokból következik, hogy a EDA1 háromszög területe . Hasonló megfontolásokból következik, hogy a EDA1 háromszög területe 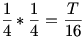 . Így a keresett B1C1DE trapéz területe . Így a keresett B1C1DE trapéz területe 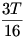 . .
HK
|
| Előzmény: [51] lorantfy, 2003-12-17 13:44:07 |
|
|
|
| [49] Suhanc | 2003-12-13 22:23:02 |
 14.
Szakköri feladat: volt, aki trigonometriával oldotta meg, volt, aki koordinátageometriával... elemi? (szerintem a legszebb)
Adott egy kör két, egymásra merőleges AC és BD átmérője; a kör középpontja O. OD szakasz felező pontja E. AE egyenese két pontban metszi a kört; ezek egyike A pont, a másik pont legyen F. BF szakasz AC átmérőt G pontban metszi. Mekkora BC és BG szakaszok aránya?
(Elnézést kérek mindenkitől, ehhez egy ábra is; sajnos ezt nem tudok készíteni.)
|
|
| [48] Rácz Béla | 2003-12-11 00:19:37 |
 13.
Igaz-e, hogy ha egy n természetes szám minden d természetes számmal osztva kvadratikus maradékot ad (olyan maradékot, ami előáll, mint egy mégyzetszőám d-s maradéka), akkor n maga is négyzetszám?
(Ez már lehet, hogy nem ujjgyakorlat:) És ha ezt csak akkor tudjuk, ha d prímszám?
|
|
|
| [46] lorantfy | 2003-12-10 14:19:59 |
 Megoldás a 11. feladatra
A háromszög területképletéből kifejezve: 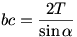 állandó. állandó.
a2=b2+c2-2bccos 
Tehát a2 akkor minimális ha b2+c2 minimális. Ezt csökkentketjük egy konstassal, a minimum helye nem változik:
b2+c2-2bc=(b-c)2 0 0
Ez akkor minimális, ha b=c, vagyis ha a háromszög egyenlő szárú.
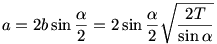
|
 |
| Előzmény: [42] evilcman, 2003-12-07 17:15:46 |
|
| [45] jenei.attila | 2003-12-10 12:46:50 |
 Kedves Suhanc!
Rendezzük át az egyenletet, és a jobboldalt alakítsuk szorzattá:
a2=b(b1998-1)
Legyen p a b egy prím osztója. Ekkor p|a2, ezért a2 prím felbontásában p páros hatványon szerepel. De p nem osztója b1998-1-nek, ezért p a b felbontásában is páros hatványon szerepel, vagyis b négyzetszám. Mivel a2 és b is négyzetszám, ezért b1998-1 is négyzetszám kell, hogy legyen. De b1998 szintén négyzetszám, ezért csak b=1 lehet, amikor a=0.
|
| Előzmény: [43] Suhanc, 2003-12-07 18:18:36 |
|
|
| [43] Suhanc | 2003-12-07 18:18:36 |
 12. feladat
Mely a; b egész számokra teljesül az alábbi egyenlőség?
a2+b=b1999
|
|
| [42] evilcman | 2003-12-07 17:15:46 |
 11. feladat
Azon háromszögek közül, amelynek adott a területe és az egyik szöge, melyikben lesz az adott szöggel szemben lévő oldal a legkisebb? Mennyi lesz?
|
|
|
| [40] lorantfy | 2003-12-07 12:49:07 |
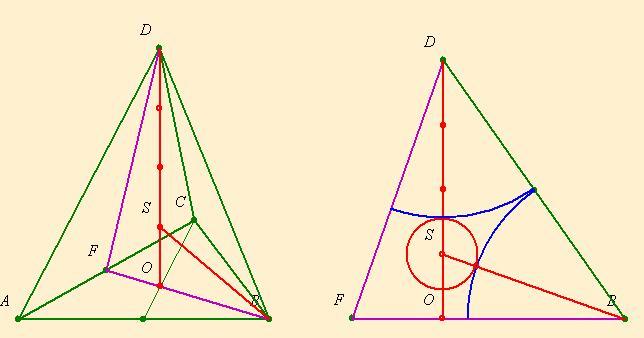
 9.feladat megoldása:
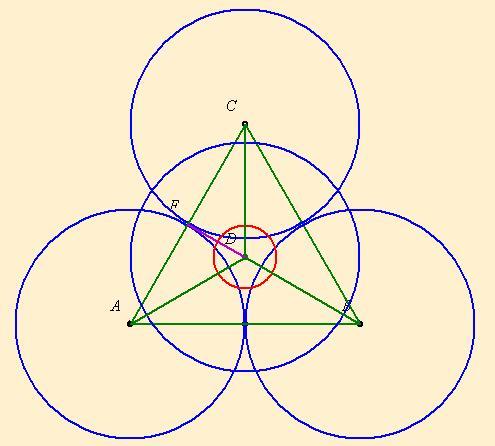
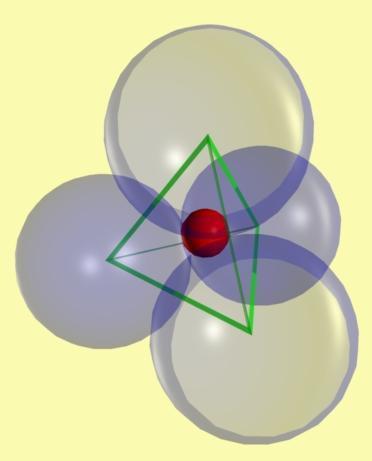
A keresett kisgömb középpontja egy szabályos tetraéder súlypontja, melynek csúcsai a nagygömbök középpontjai. A tetraéder oldalai 2R=2 egység hosszúak, magassága:
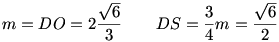
A kisgömb sugara: 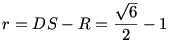 . (Az ábrákat Laci fiam készítette) . (Az ábrákat Laci fiam készítette)
|
 |
| Előzmény: [31] Hajba Károly, 2003-12-05 23:29:05 |
|
|
|
| [37] Suhanc | 2003-12-07 09:04:52 |
 László 7b)feladatára a négyzetek:
2(x+1)2+2(z+1)2+(x+y+z)2+3(z+y/2)2+5(x+y/2)2=0
Ez csak akkor teljesülhet, ha minden tag 0. Ebből x=z=-1 így y=2 nek kell lennie, ami valóban jó megoldás.
|
|
| [36] Kós Géza | 2003-12-06 09:48:31 |
 Kedves Suhanc,
 = \ge, = \ge,  = \le. = \le.
A képleteket egészben érdemes dollárjelek közé tenni, pl. $a^+2ab+b^2$ és nem $a^2$+2ab+$b^2$. A képleteken belül kicsit más a betűtípusok kezelése, a betűk alapértelmezésben dőltek, és a szóközök automatikusan kimaradnak.
|
| Előzmény: [35] Suhanc, 2003-12-06 09:21:16 |
|
| [35] Suhanc | 2003-12-06 09:21:16 |
 László 9a) feladatára van egy másfajta megoldásom:
Egy tétel kimodja, hogy a derékszögű háromszögben a befogók összege nem nagyobb az átfogó 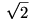 szeresénél. Ezt az alábbi módon, indirekten bizonyíthatjuk: szeresénél. Ezt az alábbi módon, indirekten bizonyíthatjuk:
TFH: a+b >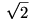 *c *c
Ekkor: a2+2ab+b2 >2c2
Vagyis: a2+2ab+ b2 > 2a2+2b2
Tehát: 0> a2-2ab+b2
0> (a-b)2 Ez ellentmondás, tehát eredeti állításunk igaz volt. Vagyis, mivel meg van adva az átfogó, így a kerület legfeljebb ennek 1+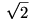 szerese lehet, abban az esetben, ha a háromszög egyenlő szárú, így a-b=0. szerese lehet, abban az esetben, ha a háromszög egyenlő szárú, így a-b=0.
(kérdés: a TeX-ben hol találom a >= jelet szépen?)
|
|
| [34] Hajba Károly | 2003-12-06 01:24:37 |
 Megoldás László 9.b feladatára:
Legyen a kúp alapjának sugara egységnyi, magassága m. Legyen továbbá a henger sugara 0<x<1.
Vhenger=x2 m(1-x)= m(1-x)= m(x2-x3) m(x2-x3)
Vhenger'= m(2x-3x2)=0 m(2x-3x2)=0
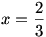
![\frac{V_{henger}}{V_{ku'p}}=\frac{\pi m \bigg[\Big(\frac23\Big)^2-\Big(\frac23\Big)^3\bigg]}{\frac{\pi m}{3}} = \frac49](keplet.cgi?k=50AD2B4C04DFC43C)
|
| Előzmény: [30] lorantfy, 2003-12-05 23:24:18 |
|
| [33] Hajba Károly | 2003-12-06 00:51:50 |
 Megoldás László 9.a feladatára:
A háromszög kerülete:
K=1+sin +cos +cos
K'=cos -sin -sin =0 =0
cos =sin =sin
 =45° =45°
Tehát, ami szemrevételezéssel is nyilvánvaló, az egyenlŐ szárú háromszögnek a legnagyobb a kerülete az egységnyi átfogójú derékszögű háromszögek közül.
HK
|
| Előzmény: [30] lorantfy, 2003-12-05 23:24:18 |
|
| [32] Hajba Károly | 2003-12-05 23:40:05 |
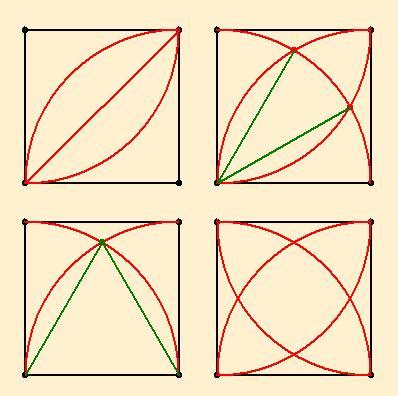
 10. feladat:
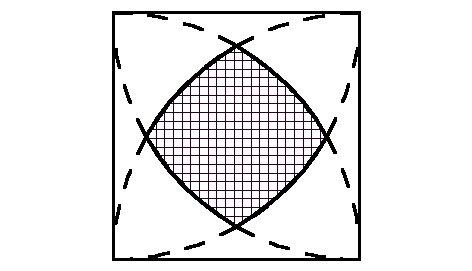
Mekkora az alábbi egységnyi oldalú négyzetbe egységnyi sugarú körívekkel szerkesztett sraffozott terület nagysága?
HK
|
 |
|
| [31] Hajba Károly | 2003-12-05 23:29:05 |
 9. feladat:
Adott 4 darab egységsugarú tömör golyónk, mely mindegyik mindegyikkel érintkezik. Mekkora az a tömör 5. golyó, mely mind a 4 darab golyót érinti?
Hajba Károly
|
|
| [30] lorantfy | 2003-12-05 23:24:18 |
 9.feladat:
a.) Adott átfogojú derékszögű háromszögek közül melyik kerülete a legnagyobb?
b.) Mekkora az adott kúpba irható hengerek térfogatának maximuma?
|
|
| [29] lorantfy | 2003-12-05 23:14:06 |
 Elnézést! Az előbbi hozzászólás rossz témába tettem!
|
|
| [28] lorantfy | 2003-12-05 23:07:00 |
 Kedves Péter, Károly és Fórumosok!
Azt hiszem a feladat szövegéből (az 5-ből 3 sapkásról van szó!) nem derült ki, hogy a börtönigazgató véletlenszerűen választ-e a sapkák közül, vagy a 7 féle minta valamelyike szerint rak fel 3-at a fejekre. (Hajlok rá, hogy ha nagy sorozatban játszaná ezt a játékot Péternek lenne igaza, hacsak nincs egy kis naptárja, amibe be van jegyezve aznap melyik mintát teszi fel a 7 közül.)
Így azt hiszem Károlynak megadhatjuk a megoldási útmutató szerinti, maximális 3-3 pontot. Péter pedig dícséretet kap "értékes megjegyzéséért"! :-)
Legközelebb beleírom az igazgató monológjába: "Most becsukott szemmel választok 3 sapkát az 5 közül, és véletlenszerűen teszem fel a fejetekre." - ,hogy pontos legyen a szöveg. (Így meg túl tudálékos lesz.)
Namost aki csak utólag olvassa a megoldást, azért érdemes átgondolni a poént. Akinek látszólag legkevesebb információja van a sapkákról - az 1. rab - annak legvalószinűbb a szabadulása. Tehát ebben az esetben, ha nincs információ (nem szólnak a hátam mögötti rabok) az is információ.
|
| Előzmény: [24] Pach Péter Pál, 2003-12-04 22:29:34 |
|




 területe 1. Legyen AB felezőpontja C1, AC felezőpontja B1, BB1 felezőpontja D, CC1 felezőpontja E. Mekkora a B1C1DE négyszög területe?
területe 1. Legyen AB felezőpontja C1, AC felezőpontja B1, BB1 felezőpontja D, CC1 felezőpontja E. Mekkora a B1C1DE négyszög területe?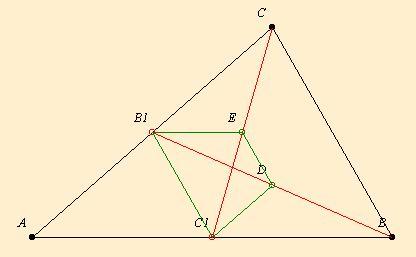
 ACF
ACF =45o, mert középponti szögpárja 90o. Tehát FG szögfelező ACF
=45o, mert középponti szögpárja 90o. Tehát FG szögfelező ACF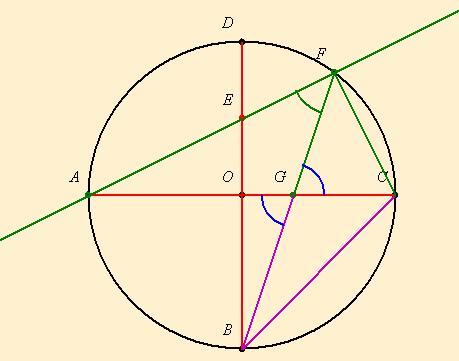



 0
0


 = \le.
= \le.  m(1-x)=
m(1-x)=