Fórum: "ujjgyakorlatok"

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Szeretnél hozzászólni? Jelentkezz be.

[628] BohnerGéza	2010-08-22 00:16:31
Súlypontban?
Előzmény: [627] Nánási József, 2010-08-21 23:06:10

[627] Nánási József	2010-08-21 23:06:10
Súlypontba szerintem.
Előzmény: [626] sakkmath, 2010-08-21 22:30:19

[626] sakkmath

2010-08-21 22:30:19

Rajzoljunk egy asztal lapjára tetszőleges háromszöget. Csúcsaiban fúrjunk egy-egy lyukat az asztalba. Fűzzünk át a lyukakon egy-egy cérnát és kössünk azok alsó végeire egy-egy súlyt. A cérnaszálak felső végeit az asztallap fölött csomózzuk össze, aztán hagyjuk, hogy a lógó súlyok a cérnaszálakat megfeszítsék. (Feltesszük, hogy a cérnák nem szakadnak el.)

Hol lesz a csomó egyensúlyi helyzete, ha a három súly egyenlő?

[625] Fernando	2010-04-14 09:36:01
Köszönni azért szabad?! :) S hogy' jött ki?
Előzmény: [622] jonas, 2010-04-13 19:12:46

[624] Fernando	2010-04-13 21:49:45
Akkor -14 éves voltam.
Előzmény: [623] Róbert Gida, 2010-04-13 20:51:03

[623] Róbert Gida	2010-04-13 20:51:03
Kürschák 2. feladata volt 1970-ben, hiperklasszikus.(komplementer eseményt kérdezte).
Előzmény: [619] Fernando, 2010-04-13 11:20:38

[622] jonas	2010-04-13 19:12:46
Várj, ezt nem értem. Ha ujjgyakorlatnak adod föl, akkor miért köszönöd a válaszunkat?
Előzmény: [620] Fernando, 2010-04-13 18:45:46

[621] jonas	2010-04-13 19:12:08
404957/511038 ?
Előzmény: [619] Fernando, 2010-04-13 11:20:38

[620] Fernando	2010-04-13 18:45:46
Válaszotokat előre is köszönöm.
Előzmény: [619] Fernando, 2010-04-13 11:20:38

[619] Fernando	2010-04-13 11:20:38
Mennyi a valószínűsége, hogy a lottón kihúzott számok között nincsenek szomszédosak?

[618] nadorp

2010-04-07 16:45:30

Ha n>1, akkor

$e-\left(1+\frac1n\right)^n=e-\sum_{k=0}^n\frac1{k!}+\sum_{k=0}^n\frac1{k!}-\left(1+\frac1n\right)^n=\sum_{k\geq n+1}\frac1{k!}+\sum_{k=2}^n\frac1{k!}\left(1-\left(1-\frac1n\right)...\left(1-\frac{k-1}n\right)\right)\geq$

$\geq\sum_{k\geq n+1}\frac1{k!}+\sum_{k=2}^n\frac1{k!}\left(1-\left(1-\frac1n\right)\right)=\left(1-\frac1n\right)\sum_{k\geq n+1}\frac1{k!}+\frac{e-2}n>\frac{e-2}n$

Előzmény: [616] Lóczi Lajos, 2010-04-07 15:20:27

[617] Lóczi Lajos	2010-04-07 15:45:30
(Nem jól mondtam: az optimalitás bizonyításához mindkét oldalon arra volt szükségem, hogy az n(e-(1+1/n)ⁿ) függvény monoton növő és limesze a végtelenben micsoda. Viszont a monotonitás nem jött ki 1-2 sorban.)
Előzmény: [616] Lóczi Lajos, 2010-04-07 15:20:27

[616] Lóczi Lajos

2010-04-07 15:20:27

Valóban, tehát az optimális konstansok a kétoldali becslésben az e-2, illetve az e/2; azaz minden n pozitív egészre

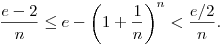
$\frac{e-2}{n}\le e-\left(1+\frac{1}{n}\right)^n<\frac{e/2}{n}.$

Az e/2 egyszerűen kijön, de Neked milyen technikával jött ki az e-2 (mert nekem csak kicsit körülményesen, monotonitási érveléssel)?

Előzmény: [615] nadorp, 2010-04-07 11:19:07

[615] nadorp

2010-04-07 11:19:07

$\frac{e-2}n\leq e-\left(1+\frac1n\right)^n$ és egyenlőség csak n=1 esetén van, tehát tetszőleges C<e-2 jó lesz.

Az is igaz, hogy bármely $C<\frac e2$ esetén "elég nagy" n-re $\frac Cn<e-\left(1+\frac1n\right)^n$

Előzmény: [614] Lóczi Lajos, 2010-03-30 15:17:31

[614] Lóczi Lajos

2010-03-30 15:17:31

Megadható-e olyan pozitív C állandó, hogy minden pozitív egész n-re

$\frac{C}{n}<e-\left(1+\frac{1}{n}\right)^n?$

Ha igen, adjunk is meg minél jobb ilyen C számot.

Előzmény: [609] Lóczi Lajos, 2010-03-20 13:00:50

[613] HoA	2010-03-30 11:48:16
Ne kötözködj, még a végén kiderül, hogy a "prím"-ség, sőt az "egész"-ség sem feltétel. A 2010 helyetti tetszőleges nemnulla egészről nem is beszélve :-)
Előzmény: [611] BohnerGéza, 2010-03-29 18:18:07

[612] Ali	2010-03-30 08:11:24
Bal oldal következik abból,hogy $\left(1+\frac{1}{n}\right)^n$ monoton növekvőleg tart e-hez, jobb oldal meg abból, hogy $\left(1+\frac{1}{n}\right)^{n+1}$ monoton csökkenőleg tart e-hez.
Előzmény: [609] Lóczi Lajos, 2010-03-20 13:00:50

[611] BohnerGéza	2010-03-29 18:18:07
És ha p számjegyei közt van 0, 1 vagy 2?
Előzmény: [610] Lóczi Lajos, 2010-03-29 02:36:39

[610] Lóczi Lajos

2010-03-29 02:36:39

Igazoljuk, hogy ha p olyan prím, amelynek (10-es számrendszerbeli alakja) nem tartalmaz sem 0-t, sem 1-et, sem 2-t, akkor az

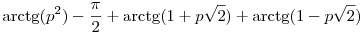
${\rm{arctg}}(p^2)-\frac{\pi}{2}+{\rm{arctg}}(1+p\sqrt{2})+{\rm{arctg}}(1-p\sqrt{2})$

szám osztható 2010-zel.

[609] Lóczi Lajos

2010-03-20 13:00:50

Igaz-e, hogy ha n pozitív egész és e az Euler-állandó, akkor

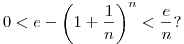
$0<e-\left(1+\frac{1}{n}\right)^n< \frac{e}{n}?$

[608] jenei.attila

2010-02-24 10:50:01

Ez így rosszabb lett. Na mégegyszer:

(ax²+by²)(x+y)=(ax³+by³)+xy(ax+by)

(ax³+by³)(x+y)=(ax⁴+by⁴)+xy(ax²+by²)

(ax⁴+by⁴)(x+y)=(ax⁵+by⁵)+xy(ax³+by³)

Előzmény: [607] jenei.attila, 2010-02-24 10:45:50

[607] jenei.attila

2010-02-24 10:45:50

Elírás történt, ráadásul a copy-paste miatt több helyen is. Az első 3 egyenlet helyesen:

(ax2+by2)(x+y)=(ax3+by3)+xy(ax+by)

(ax3+by3)(x+y)=(ax4+by4)+xy(ax2+by2)

(ax4+by4)(x+y)=(ax5+by5)+xy(ax3+by3)

Előzmény: [606] jenei.attila, 2010-02-24 10:33:26

[606] jenei.attila

2010-02-24 10:33:26

Nem számoltam ki külön x,y,a,b-t. Az én megoldásom: szorozzuk (x+y)-nal a feltételben szerelő kifejezéseket:

(ax²+by²)(x+y)=(ax³+bx³)+xy(ax+by)

(ax³+by³)(x+y)=(ax⁴+bx⁴)+xy(ax²+by²)

(ax⁴+by⁴)(x+y)=(ax⁵+bx⁵)+xy(ax³+by³)

Írjuk be a feltételekből ismert értékeket és vezessük be a t:=x+y és v:=xy helyettesítéseket.

7t=16+3v

16t=42+7v

42t-16v=(ax⁵+bx⁵)

Ebbből t=-14, v=-38, (ax⁵+bx⁵)=20 adódik.

Előzmény: [605] Róbert Gida, 2010-02-23 20:47:40

[605] Róbert Gida	2010-02-23 20:47:40
Kipróbáltam, hogy a computeralgebrai rendszerek vajon meg tudják-e oldani a feladatot, és igen, a Mathematica 5.1 egyből kiadta a két megoldást (a<->b, x<->y cserével is megoldást kapunk). Maple 12 is megoldja, de itt még egy allvalues parancs is kell a solve-hoz, mert rootof-okkal tér vissza. 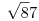$\sqrt 87$ van a,b,x,y-ban.
Előzmény: [604] jenei.attila, 2010-02-23 08:26:24

[604] jenei.attila	2010-02-23 08:26:24
Egyébként ha a Fibonacci sorozat zárt alakjára gondolunk, akkor látszik, hogy ez a sorozat is egy másodrendű lineáris homogén rekurzió zárt alakja, amely karakterisztikus egyenletének két gyöke éppen x és y, az a,b pedig a két első tag által meghatározott konstansok. A rekurzív képletben szereplő konstansok meghatározhatók a sorozat első 4 tagjából. Nem így oldottan meg a feladatot, de ez is egy lehetséges megoldás lenne.
Előzmény: [603] jenei.attila, 2010-02-23 08:16:10

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Már regisztráltál?
Új vendég vagy?