Fórum: "ujjgyakorlatok"

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Szeretnél hozzászólni? Jelentkezz be.

[403] Lóczi Lajos	2005-10-30 23:11:46
Ügyes (amit leírtál numerikusan, azok úgy is vannak és be is lehet pontosan bizonyítani).
Előzmény: [402] ágica, 2005-10-30 22:02:05

[402] ágica	2005-10-30 22:02:05
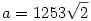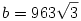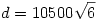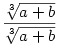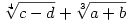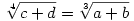Legyen $a=1253\sqrt2$ , $b=963\sqrt3$ , c=26209, $d=10500\sqrt6$ , az egyszerűség kedvéért. A feladatban lévő összeg első tagját beszoroztam $\frac{\root3\of{a+b}}{\root3\of{a+b}}$ -vel, a második tagot pedig hasonló módon szorozva, majd közös nevezőre hozva és egyszerűsítve kaptam, hogy az eredeti összeg egyenlő a $\root4\of{c-d}+\root3\of{a+b}$ kifejezéssel. 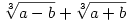Ebből arra gondoltam, hogy $\root4\of{c+d}=\root3\of{a+b}$ , és a számológépem ebben a gondolatban megerősített :) Tehát az eredeti kifejezést végülis felírtam $\root3\of{a-b}+\root3\of{a+b}$ alakban, ami viszont felírható $\frac{2a}{{(a+b)}^{2/3}-{(a^2-b^2)}^{1/3}+{(a-b)}^{2/3}}$ formában is. Itt a nevező értékére a számológép kereken 179-et hozott ki, és ebből adódott az eredményem, ami persze lehet, hogy a számológép használatából adódó pontatlanságok miatt végülis hibás :)
Előzmény: [395] Lóczi Lajos, 2005-10-30 20:07:02

[401] Lóczi Lajos

2005-10-30 21:36:47

82. feladat. Valamely $\alpha$ $\in$ [0,1] esetén tekintsük az $e_n:=\left(1+\frac{1}{n}\right)^{n+\alpha}$ sorozatot. Határozzuk meg a fenti $\alpha$ -k közül mindazokat, melyekre az e_n sorozat

a.) monoton növő, illetve b.) monoton fogyó.

[400] lorantfy

2005-10-30 21:35:45

Kedves Suhanc!

Szép megoldás! Grat! Ahhoz képest, hogy a sárga feladatgyüjteményből van elég húzós!

Nekem dupla helyettesítéssel sikerült. Az elsővel szimmetrikus negyedfokúvá alakul, majd a szokásos módszerrel másodfokú lesz.

Ha lesz időm holnap beírom.

Előzmény: [388] Suhanc, 2005-10-30 12:46:17

[399] Lóczi Lajos	2005-10-30 21:19:45
81. feladat. Legyen f₀=0 és f₁=1, továbbá legyen 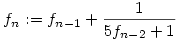$f_n:=f_{n-1}+\frac{1}{5f_{n-2}+1}$ . Döntsük el, hogy f_n felülről korlátos-e.

[398] Lóczi Lajos

2005-10-30 21:17:15

80. feladat. Adjuk meg, mennyi lesz az alábbi végtelen tört értéke:

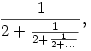
$\frac{1}{2+\frac{1}{2+\frac{1}{2+ ...}}} ,$

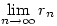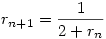azaz mennyi $\lim_{n\to \infty}r_n$ , ha r₁=1/2 és $r_{n+1}=\frac{1}{2+r_n}$ ? Bizonyítsuk is be az eredményt.

[397] Lóczi Lajos

2005-10-30 21:09:38

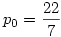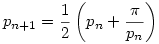79. feladat. Tekintsük azt a p_n sorozatot, amelyre $p_0=\frac{22}{7}$ és $p_{n+1}=\frac{1}{2}\left(p_n+\frac{\pi}{p_n} \right)$ .

a.) Mi lesz $\lim_{n\to \infty} p_n$ ?

b.) Adjuk meg p₂₀₀₅ pontos értékét. (A válaszban tehát konstansokat és elemi függvényeket használhatunk, de a p_n sorozat elemeit nem).

c.) Mi lesz $\lim_{n\to \infty} p_n$ , ha a fenti 22/7 helyett p₀:= -10¹⁰ ?

[396] Lóczi Lajos

2005-10-30 20:46:24

78. feladat. Valamely a>0 szám esetén értelmezzük az x_n sorozatot a következőképpen:

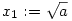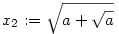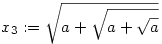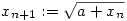x₀:=0, $x_1:=\sqrt{a}$ , $x_2:=\sqrt{a+\sqrt{a}}$ , $x_3:=\sqrt{a+\sqrt{a+\sqrt{a}}}$ , és általában, $x_{n+1}:=\sqrt{a+x_n}$ .

a.) Lássuk be, hogy az x_n sorozat konvergens. Jelölje a határértékét A. Fejezzük ki A-t a segítségével.

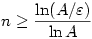b.) Mutassuk meg, hogy ha $\varepsilon$ >0 tetszőleges valós szám és $n\ge \frac{\ln(A/\varepsilon)}{\ln A}$ , akkor a hiba legfeljebb $\varepsilon$ , azaz |x_n-A| $\le$ $\varepsilon$ .

c.) Viszont ha 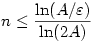$n\le \frac{\ln(A/\varepsilon)}{\ln(2 A)}$ , akkor a hiba legalább $\varepsilon$ , azaz $\varepsilon$ $\le$ |x_n-A|.

[395] Lóczi Lajos	2005-10-30 20:07:02
Kíváncsi vagyok (csak címszavakban), hogy a "némi számolás" milyen típusú számolásra, módszerre utal.
Előzmény: [390] ágica, 2005-10-30 14:53:11

[394] Lóczi Lajos	2005-10-30 19:58:16
A [377]-es hozzászólásban megfogalmazott sejtés alapján ez már gyerekjáték :) Az egyenletnek nincs megoldása, mert modulo 11 megoldhatatlan.
Előzmény: [393] Edgar, 2005-10-30 19:32:45

[393] Edgar

2005-10-30 19:32:45

Nem tudom, szerepelt-e ez már... ha igen, elnézést :-)

Igazi gonosz kis ujjgyakorlat... Oldd meg a természetes számok körében:

x⁵-y²=4

[392] Edgar	2005-10-30 19:21:55
így van :-) okosabb vagy, mint a nagykemény Maple szoftver... azaz ezer matematikusnál okosabb :-P ("Command the Brillance of a thousand mathematicians") azt hittem, majd befejti nekem, de magad uram lett belőle...
Előzmény: [390] ágica, 2005-10-30 14:53:11

[391] lorantfy

2005-10-30 18:41:50

Igazad van!

A 32.tesztfeladathoz kiegészítő kérdés: Hányadik tizedesjegytől ismétlődik a Fibonacci sorozat tagjaiból az ott leírt módon készített végtelen összeg racionális értéke.

Előzmény: [389] Lóczi Lajos, 2005-10-30 13:32:48

[390] ágica	2005-10-30 14:53:11
Némi számolás után kijött, hogy a kifejezés egyenlő 14*gyök2-vel, tehát irracionális :)
Előzmény: [386] Lóczi Lajos, 2005-10-30 01:27:22

[389] Lóczi Lajos

2005-10-30 13:32:48

Nem következik, hogy nincs igaza!

Egy racionális számban nemcsak az első pár tizedeshelyen levő "89" alkothatja az ismétlődő részt, ezért a hozzászólásodból a "szebb" szó törlendő :)

Előzmény: [387] lorantfy, 2005-10-30 11:22:22

[388] Suhanc

2005-10-30 12:46:17

Kedves László!

Egy lehetséges megoldás:

Végezzük el egyenletünkkel a következő átalakításokat (x<>-5)!

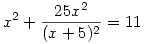
$x^2 +\frac{25x^2}{(x+5)^2}= 11$

x²(x+5)²+25x²=11(x+5)²

x²(x+5)²+25x²+25(x+5)²=36(x+5)²

(x+5)²[x²+25]+25x²=36(x+5)²

(x+5)⁴-10x(x+5)²+25x²=36(x+5)²

[(x+5)²-5x]²=(6x+30)²

Ahonnan a²-b²=(a+b)(a-b) azonosságot felhasználva, és rendezve a tényezőket kapjuk, hogy:

(x²+11x+55)(x²-x-5)=0

Nyilván: x²+11x+55>0

Ezért csak x²-x-5=0 lehetséges, melyet

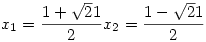$x_1 = \frac{1+\sqrt21}{2} x_2 = \frac{1-\sqrt21}{2}$ gyökök teljesítenek.

Előzmény: [382] lorantfy, 2005-10-29 11:54:41

[387] lorantfy

2005-10-30 11:22:22

Nincs igaza, mert ha egy pontosabb géppel számolja rögtön kiderül, hogy a 89 számpár nem ismétlődik: 19,798989873223330683223642138936

Szebb indoklásra még várni kell!

Mindenesetre ha racionális szám lenne, akkor ez lenne az értéke: 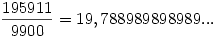$\frac{195911}{9900}=19,788989898989...$

Előzmény: [386] Lóczi Lajos, 2005-10-30 01:27:22

[386] Lóczi Lajos

2005-10-30 01:27:22

77. feladat. Valaki számológéppel azt találta, hogy

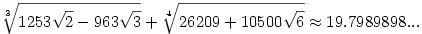
$\root3 \of{ 1253{\sqrt{2}} - 963{\sqrt{3}} } + \root 4 \of{ 26209 + 10500{\sqrt{6}} }\approx 19.7989898...$

amiből azt sejti, hogy a fenti szám racionális. Igaza van-e?

[385] Lóczi Lajos	2005-10-29 22:49:03
$\frac{-11 \pm 3i {\sqrt{11}}}{2}$ például megoldás, ahol i a komplex képzetes egység.
Előzmény: [384] lorantfy, 2005-10-29 22:18:31

[384] lorantfy

2005-10-29 22:18:31

A racionális számok körében sincs. :-)

Helyettesítéssel kellene visszavezetni másodfokúra!

Előzmény: [383] Lóczi Lajos, 2005-10-29 22:01:15

[383] Lóczi Lajos	2005-10-29 22:01:15
Az egész számok körében nincs megoldás :)
Előzmény: [382] lorantfy, 2005-10-29 11:54:41

[382] lorantfy

2005-10-29 11:54:41

76. feladat: Oldjátok meg az egyenletet:

$x^2+\frac{25x^2}{(x+5)^2}=11$

[381] Róbert Gida

2005-10-29 02:12:14

Sokkal egyszerübben is meg lehet oldani ezeket, ha lnko(p,q)>1 most itt x⁵⁹+y⁵⁹=3, feltehető a szimmetria miatt, hogy x $\geq$ 0>y, továbbá x⁵⁹=3+(-y)⁵⁹ miatt, hogy x>-y, de akkor x⁵⁹+y⁵⁹ $\geq$ x⁵⁹-(x-1)⁵⁹, de ez x-ben nyilván monoton nő, x=0;1-re nincs megoldás és x $\geq$ 2-re x⁵⁹+y⁵⁹ $\geq$ 2⁵⁹-1, így nincs megoldás.

Ez általánosítható arra az esetre is, ha d=lnko(p,q)>1, használjuk, hogy a szomszédos d-edik hatványok különbsége monoton nő,mint az előbb és ha x ismert, akkor az egyenletből abs(y) is megkapható, így az egyenletnek véges sok megoldása lehet legfeljebb.

Az általános esetben feltehető, hogy p vagy q páratlan , különben lnko(p,q) $\geq$ 2 teljesül. Legyen például q páratlan, ekkor az egyenlet átírható ( az új y legyen a régi -y ).Az egyenlet

x^p-y^q=k

, ahol k nem nulla, akkor az egyenletnek minden k-ra véges sok megoldása van, ez S. S. Pillai sejtése, máig megoldatlan.

Előzmény: [373] nadorp, 2005-10-27 09:55:27

[380] Lóczi Lajos	2005-10-28 23:19:38
Igen, ezek a számok pár napja jó ismerőseim. :) (Az is érdekes kérdés még, hogy a minimális cáfolómodulushoz tartozó "alkalmas n-ek" halmaza micsoda, hányelemű, stb., de ez nyilván bonyolultabb kérdés lenne.)
Előzmény: [379] Ali, 2005-10-28 14:46:34

[379] Ali

2005-10-28 14:46:34

Mégegyszer átolvasva minmod(p,q) definícióját, és "alkalmas n"-hez keresve a minimális modulusokat ez jön ki:

minmod(3,3)=7

minmod(5,5)=11

minmod(7,7)=29

minmod(11,11)=23

minmod(13,13)=53

minmod(17,17)=103

minmod(19,19)=191

minmod(23,23)=47

minmod(29,29)=59

minmod(31,31)=311

minmod(37,37)=149

minmod(41,41)=83

minmod(43,43)=173

minmod(47,47)=283

Ebből valóban adódik a 2/a sejtés.

Előzmény: [378] Ali, 2005-10-28 12:00:54

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]

Már regisztráltál?
Új vendég vagy?