| [1040] szabótimi | 2008-05-11 16:41:50 |
 Üdvözlet! Ha valakinek van egy kis ideje kérem segítsen hogyan oldható meg ez a számomra bonyolult feladat! Nagyon fontos lenne!Kérlek titeket!Előre is köszi! A feladat: Ábrázoljuk a PQR háromszög köré írt kört. Szerkesszük meg a lényeges átmérők mindkét képét a végpontokhoz tartozó érintőkkel együtt, és állítsuk elő az érintőket a háromszög csúcsaiban is. Rajzoljuk meg a vetületi görbéket. P(45, 140, 265); Q(45, 40, 205); R(145, 140, 205).
|
|
| [1039] HoA | 2008-05-08 22:34:33 |
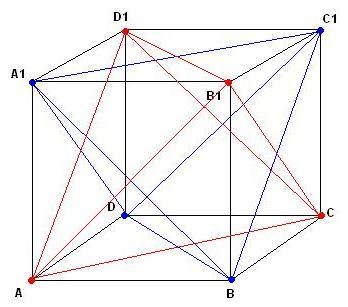
 A piros tetraédet - pontosabban annak B1-ben összefutó három lapját - a kék tetraéder A1BC1 lapja egy szabályos háromszögben metszi. A háromszög oldalai az ABB1A1 , BCC1B1 és A1B1C1D1 lapok középpontjait egymással összekötő három szakasz. Az alakzat szimmetriája miatt ez mind a nyolc csúcsról megállapítható. A közös részt tehát 8 szabályos háromszög határolja. A neve oktaéder. Lásd pl. http://mbuttons.bolyai.hu/upload/VRML/palyazat/kapcs.htm : Egy kocka megfelelő lapátlói szabályos tetraédert alkotnak. A két így kapott tetraéder közös része egy szabályos oktaéder.
|
| Előzmény: [1038] Mate~, 2008-05-08 18:47:50 |
|
| [1038] Mate~ | 2008-05-08 18:47:50 |
 zsolla feladatának megoldása engem is érdekelne, van rá egy gondolatom, csak 2 pontom helyzete bizonytalan. Tudtok segíteni? Itt egy gyorsan összedobott ábra:
|
 |
|
| [1037] Mate~ | 2008-05-08 17:47:13 |
 133: Én most hirtelen csak a P-t látom: ABG háromszög egybevágó BCD háromszöggel, hiszen BG=BC, AB=BD és ABGszög= CBDszög (derékszög). Mivel AB merőleges DB-re és BG merőleges BC-re, AG-nek is merőlegesnek kel lennie CD-re. Tehát az APCszög derékszög, így az APC háromszög derékszögű. Thalesz miatt pedig a P pontnak rajta kell lennie a k3 körön. A többin még agyalok. :)
|
| Előzmény: [1034] HoA, 2008-05-05 18:18:51 |
|
| [1036] zsolla | 2008-05-08 13:55:43 |
 Keresem a következő feladat megoldását: Az ABCD A1B1C1D1 kocka A C B1 D1 csúcsai és az A1 C1 B D csúcsai is egy-egy tetraédert határoznak meg. Milyen test lesz a két tetraéder közös része?
|
|
| [1035] BohnerGéza | 2008-05-06 22:01:00 |
 Érdekesség a 133. feladathoz: Az A-t és C-t rögzítsük! B-t mozgatva AB-n a kapott DR egyenesek átmennek egy közös ponton.
Fogalmazzuk meg a fentinek megfelelő másik állítást is!
Igazoljuk az állítást!
|
| Előzmény: [1034] HoA, 2008-05-05 18:18:51 |
|
| [1034] HoA | 2008-05-05 18:18:51 |
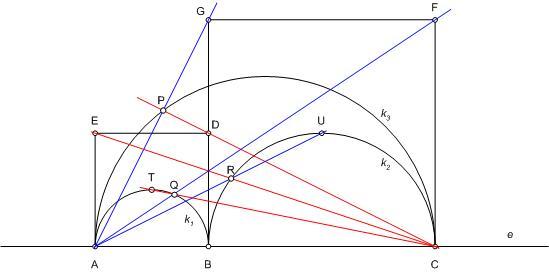
 133.feladat-nak javaslom az alábbit: Egy e egyenes 3 pontja ebben a sorrendben A, B és C. Vegyük fel az egyenes egyik oldalán a T középpontú ABDE és az U középpontú BCFG négyzeteket, valamint az AB átmérőjű k1 , BC átmérőjű k2 és AC átmérőjű k3 félköröket.
a) Igazoljuk, hogy az AG és CD egyenesek P metszéspontja k3-ra, az AU és CE egyenesek R metszéspontja k2-re, az AF és CT egyenesek Q metszéspontja k1-re esik.
b) Mi jellemzi a P, Q, R ponthármast?
|
 |
|
| [1033] BohnerGéza | 2008-04-29 19:18:38 |
 Az itteni 132. feladat egy - inverzióval történő - megoldása látszik a "Valaki mondja meg!" témában lévő [479]. hozzászólásából. Néhány "elemibb" már itt, az előző hozzászólásokban megszületett. Köszönöm!
|
| Előzmény: [1032] HoA, 2008-04-29 13:28:03 |
|
| [1032] HoA | 2008-04-29 13:28:03 |
 Ha az elemibb megoldást a 3 érintkező kört érintő kör szerkeztésére gondolod, egyelőre nem látom az utat. A Geometriai feladatok gyűjteménye az általános Apolloniusz feladatot oldja meg középiskolában tanult módszerekkel:
-az adott és a szerkesztendő körök növelésével-zsugorításával visszavezeti a feladatot két kört (k1,k2) érintő, adott P ponton áthaladó ke kör szerkesztésére - F2 ( elfajuló esetekben egy kör és két pont, illetve 3 pont)
-F2 megoldása során megszerkeszti a körök egyik hasonlósági pontját P-vel összekötő egyenesnek másik, ke-re illeszkedő pontját (Q)
-Végül megszerkeszti a két adott ponton (P, Q) áthaladó, pl. k1-et érintő kört. Ez a megoldás elemibb abban az értelemben, hogy nem használ inverziót, viszont sokkal hosszadalmasabb. És ami a fő baj, nem használja ki azt a speciális helyzetet, hogy a 3 adott kör érinti egymást. F2 megoldása során előjönnek az érintési pontok és a hasonlósági pont közötti kapcsolatok, de nem látom, esetünkben hogyan lehetne alkalmazni.
|
| Előzmény: [1022] BohnerGéza, 2008-04-27 15:01:30 |
|
|
| [1031] Káli gúla | 2008-04-28 19:34:24 |
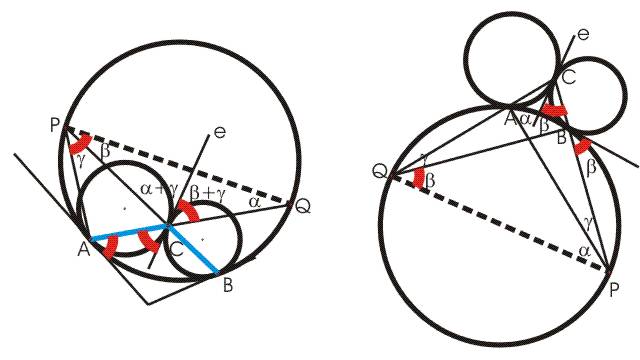
 Jelölje az átmérőgyanús pontokat P és Q. A PQ ívet a két érintési pont, A, B három körívre bontja, az ezekhez tartozó kerületi szögek legyenek  , ,  és és  . Ekkor a CPQ háromszög szögösszege 2 . Ekkor a CPQ háromszög szögösszege 2 +2 +2 +2 +2 , mert az e közös érintő a C-nél lévő szöget a bal oldali ábrán ( , mert az e közös érintő a C-nél lévő szöget a bal oldali ábrán ( + + ) és ( ) és ( + + ) részre, a jobb oldali ábrán ) részre, a jobb oldali ábrán  és és  részre osztja (a sima és az elfajult kerületi szögek egyenlőségét kell a közös érintőknél figyelembe venni). Tehát 2 részre osztja (a sima és az elfajult kerületi szögek egyenlőségét kell a közös érintőknél figyelembe venni). Tehát 2 +2 +2 +2 +2 =180o, azaz a három körív együtt egy félkört alkot. =180o, azaz a három körív együtt egy félkört alkot.
Elnézést a többszörös beírásért, az előző három, képtelen hozzászólásomat ki is lehetne törölni. Ha egy moderátor olvassa, köszönöm előre is. (törölve - Sirpi)
|
 |
| Előzmény: [1020] BohnerGéza, 2008-04-27 03:22:52 |
|
| [1029] HoA | 2008-04-28 17:46:08 |
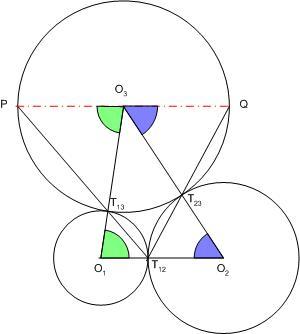
 Az állítás abból adódik, hogy két érintkező kör érintési pontja egyben a két kör kölső vagy belső hasonlósági pontja is. Talán jobban áttekinthető kívülről érintkező körökre, ekkor az érintési pont belső hasonlósági pont. Az ábrán a hasonlóság miatt PO3||T12O1ésQO3||T12O2. Mivel O1,O2ésT12 egy egyenesen vannak, ezért P,QésO3 is, vagyis PQ a kör átmérője.
|
 |
| Előzmény: [1019] BohnerGéza, 2008-04-27 02:52:47 |
|
|
| [1024] Gyarmati Péter | 2008-04-28 16:36:16 |
 Nem használtam fel azt, hogy az E érintési pont. Lehet, hogy felhasználtam a bizonyításban a bizonyítandó állítást?!
Így túl elemi volna...
|
|
|
|
|
|
| [1019] BohnerGéza | 2008-04-27 02:52:47 |
 132. feladat: Három kör páronként érinti egymást három, nem egy egyenesen lévő pontban. Két kör érintési pontján át húzzunk egy-egy egyenest a másik két ponton át! Bizonyítsuk be, hogy ezeknek a harmadik körrel való másik metszéspontja a kör két átellenes pontja!
|
|
| [1018] HoA | 2008-04-21 09:25:28 |
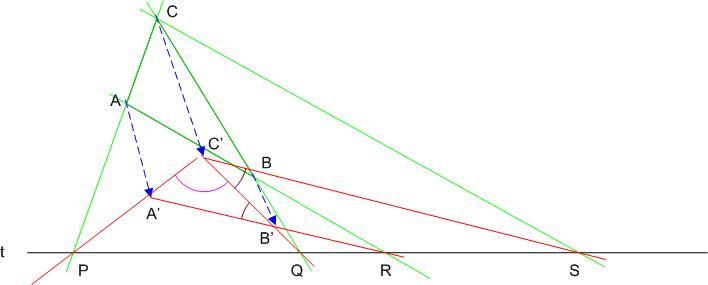
 Legyen A'B'C' az ABC háromszög képe az affinitásnál. Ekkor A'B'C' oldalegyenesei is a P, Q, R pontokban metszik a t tengelyt. Az affinitás párhuzamosság-tartró tulajdonsága miatt C'S és A'R párhuzamosak. Ezért A'B'C' szög és B'C'S szög váltószögek, egyenlőek. Így C' pontból a QS szakasz az egyik adott (béta), PQ pedig a másik adott - én C'-nél lévő szög miatt gammának nevezném - szög alatt látszik. Ebből a leírt szerkesztés már adódik.
|
 |
| Előzmény: [1014] HoA, 2008-04-20 08:50:18 |
|
|
|
| [1015] HoA | 2008-04-20 08:58:50 |
 Ha geometriai feladatról van szó, vegyük fel a Q pontot tartalmazó, PQ szakaszra merőleges S síkot. Ebben a síkban rajzoljunk egy Q középpontú, 35 mm oldalú négyzetet. A négyzet csúcsai és P alkotják a keresett gúlát.
Ha ábrázoló geometria, akkor javaslom, tedd fel abba a fórumba.
|
| Előzmény: [1012] t.balint8911, 2008-04-19 13:25:19 |
|
| [1014] HoA | 2008-04-20 08:50:18 |
 Kedves Cocka!
Egyelőre, hogy ne bosszankodj tovább, a válasz kérdésedre: az adott látószögű köríveket PQ és QS fölé kell rajzolni. Itt most nincs rajzoló programom, úgyhogy ábra és indiklás holnap.
|
| Előzmény: [1013] cocka, 2008-04-20 00:42:09 |
|
| [1013] cocka | 2008-04-20 00:42:09 |
 Nekem is lenne egy érdekes kérdésem a kedves matematikát szerető kollégákhoz.
Konkrétan egy geometriai feladatról van szó, azonbelül is egy tengelyes affinitásról.
A szövege a következő:
Adott a tengelyes affinitás tengelye és egy ABC háromszög. Határozzuk meg az affinitást úgy, hogy az A'B'C' hasonló legyen egy előre megadott DEF háromszöghöz.
Hát ugye az ember próbálkozik, de sajnos nekem nem jött össze. A megoldás szerint a szerkesztés lépései a következők:
Megrajzolom a t tengelyt. Megrajzolom az ABC háromszöget úgy, hogy az oldalait meghosszabbítom. CA P-ben, CB Q-ban, AB R-ben, az AB-vel a C-n keresztül húzott párhuzamos egyenes pedig S-ben metszi a tengelyt.
Az ABC háromszög mellé valahova megrajzolom a DEF háromszöget. Az F szögét elnevezem alfának, az E szögét meg bétának. A megoldás azt javasolja, hogy a PQ szakasz fölé (alá) szerkesszünk az alfa szöggel látószög körívet, illetve az RS fölé (alá) is szerkesszünk egy látószög körívet a béta szöggel. Na most elvileg a látószög körívek metszéspontja fogja kiadni a C' helyét. Ekkor ugye a feladat tovább úgy folytatódik, hogy a C'-t összekötöm a C-vel és ez lesz az affinitás iránya.
Igen ám, na de akármilyen helyzetű az ABC háromszög ez a két kör így a büdös életben nem fogja metszeni egymást. (az sem mellékes egyébként, hogy a megoldásban ez az egész feladat 3 sorban el van intézve a szerkesztési lépéseket erősen mellőzve, sőt ábra sincs, nehogy már megértsd :( )
Szóval a kérdésem végül is az lenne, hogy mely szakaszok fölé is kéne a látószög köríveket szerkeszteni, mert a PQ és RS páros biztosan nem nyerő. Próbáltam úgy is, hogy PR és QS, így metszi a két körív egymást, de a kapott háromszög rohadtul nem hasonlít a DEF háromszögre, mert pl. a szögeik kapásból nem egyeznek meg. Én meg valami olyasmit hallottam a hasonló háromszögekről, hogy szögei páronként megegyeznek.
A feladattal bohóckodtam egy sort Geogebrában, aztán hagytam az egészet a francba. Akinek van valami ötlete ne kíméljen. Akár privátban is. Thanks.
|
 |
|
| [1012] t.balint8911 | 2008-04-19 13:25:19 |
 Tisztelt forumozók !
Nem tudom hogyan áljak neki ennek a feledatnak:
Adott a PQ szakasz . Szerkeszen egy olyan szabályos négyoldalú gúlát , amelynek P a csucspontja, Q pedig a 35 mm élű alapnégyzetnek a középpontja !
|
|
|
| [1010] sakkmath | 2008-04-15 11:47:19 |
 A Ptolemaiosz-tétel általánosabb változata:
Ha egy négyszög oldalai a, b, c és d, átlói e és f, akkor ac+bd  ef, és egyenlőség akkor áll, ha a négyszög húrnégyszög. (Az egyenlőtlenség bal oldalán a szemközti oldalak szorzatának összege áll.) ef, és egyenlőség akkor áll, ha a négyszög húrnégyszög. (Az egyenlőtlenség bal oldalán a szemközti oldalak szorzatának összege áll.)
|
| Előzmény: [1009] akinom91, 2008-04-15 11:22:48 |
|
| [1009] akinom91 | 2008-04-15 11:22:48 |
 Volt egy tetel, mar nem is tudom pontosan kirol neveztek el (talan Descartes, de nem vagyok biztos benne), amely szerint egy negyszog atloinak paronkenti szorzata egyenlo, vagy legalabbis valami ilyesmi. Tudna valaki segiteni a pontos megfogalmazasaban, alkalmazasaban?
|
|
| [1008] Káli gúla | 2008-04-15 00:15:26 |
 Legyen az ABCD tetraéder AB élén atmenő szögfelező síkról szó., messe ez a CD-t E-ben. Húzzunk C-n és D-n át (c és d) párhuzamos egyeneseket az AB szakasszal. A c és d által meghatározott sík messe a szögfelező síkot e-ben. Legyen még az AB egyenes neve l. Ezzel a négy párhuzamos egyenessel (l, c, d, e) tulajdonképpen visszavezettük a két dimenziós kérdésre a feladatot:
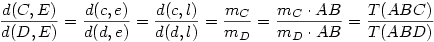
(A második egyenlőségnél használtuk a kétdimenziós tételt, abban a síkban, amelyik a négy párhuzamosra merőleges.)
|
| Előzmény: [1006] Gyöngyő, 2008-04-14 22:45:39 |
|
|
| [1006] Gyöngyő | 2008-04-14 22:45:39 |
 Sziasztok!
Tudnátok segíteni a következő feladatnál:
Bizonyítsa be,hogy a tetraéder lapszögfelező síkja olyan arányban osztja az átellenes élet,amely egyenlő annak a két lapnak a területarányával,amelyek szögét felezi!
Köszike:
Zsolt
|
|
| [1005] BohnerGéza | 2008-04-13 20:22:04 |
 Legyen a 131. feladatban H ill. J az A'B'-nek B'-höz ill. C'D'-nek D'-höz közelebbi harmadolópontja.
Igazoljuk, hogy H, B, D és J egy egyenesen vannak!
Adjuk meg a HB, a BD és a DJ szakaszok hosszának arányát!
|
| Előzmény: [1004] HoA, 2008-04-03 11:20:44 |
|
| [1004] HoA | 2008-04-03 11:20:44 |
 A 131. feladat megoldása:
a ) I.) A csúcspontok helyvektoraira - AB' felezőpontja B - felírható: 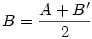 B'=2.B-A , hasonlóan C'=2.C-B , D'=2.D-C és A'=2.A-D . Az egyenletrendszert pl. D-re megoldva kapjuk: B'=2.B-A , hasonlóan C'=2.C-B , D'=2.D-C és A'=2.A-D . Az egyenletrendszert pl. D-re megoldva kapjuk:
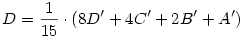 Ha koordinátarendszerünk kezdőpontjának D'-t választjuk, akkor Ha koordinátarendszerünk kezdőpontjának D'-t választjuk, akkor 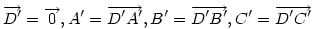 , ,
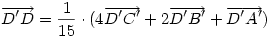 , ami A'B'C'D' négyszöget ismerve könnyen szerkeszthető. , ami A'B'C'D' négyszöget ismerve könnyen szerkeszthető.
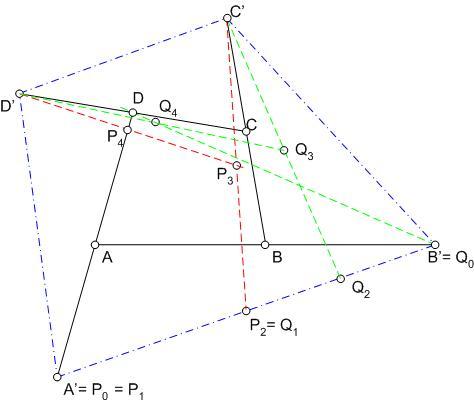
II.) Szemléletesebb megoldást kapunk, ha - mint BohnerGéza is a kiegészítésben utalt rá - a feladatban kínálkozó középpontos hasonlóságokat nézzük. Legyen H1 a  1=1/2 arányú, A' középpontú hasonlóság. Ez D-t A-ba képezi le. A H2,H3ill.H4 , mind 1=1/2 arányú, A' középpontú hasonlóság. Ez D-t A-ba képezi le. A H2,H3ill.H4 , mind  2= 2= 3= 3= 4=1/2 arányú, B' , C' ill. D' középpontú hasonlóságok A-t B-be, B-t C-be, ill. C-t D-be képezik le. A négy hasonlóság eredője (szorzata) H5=H1.H2.H3.H4 tehát D-t fixen hagyja. Mivel 4=1/2 arányú, B' , C' ill. D' középpontú hasonlóságok A-t B-be, B-t C-be, ill. C-t D-be képezik le. A négy hasonlóság eredője (szorzata) H5=H1.H2.H3.H4 tehát D-t fixen hagyja. Mivel  1. 1. 2. 2. 3. 3. 4=1/16 4=1/16 1,H5 is egy középpontos hasonlóság, amelynek csak a középpontja fixpont, tehát D H5 középpontja. Felhasználva, hogy adataink alapján H1,H2,H3ésH4 a sík tetszőleges pontjára végrehajtható, valamint hogy középpontos hasonlóságnál egy pont, a képe és a hasonlóság középpontja egy egyenesen van, az alábbi szerkesztés adódik: 1,H5 is egy középpontos hasonlóság, amelynek csak a középpontja fixpont, tehát D H5 középpontja. Felhasználva, hogy adataink alapján H1,H2,H3ésH4 a sík tetszőleges pontjára végrehajtható, valamint hogy középpontos hasonlóságnál egy pont, a képe és a hasonlóság középpontja egy egyenesen van, az alábbi szerkesztés adódik:
Vegyünk fel egy P0 és egy Q0 pontot. P0 képe H1-nél P1 , P1-é H2-nél P2, P2-é H3-nál P3, végül P3-é H4-nél P3. Hasonlóan kapjuk a Q1,Q2,Q3,Q4 pontokat. P0P4 és Q0Q4 egyenesek metszéspontja D.
P0 és Q0 ügyes megválasztásával a lépések száma csökkenthető. Például legyen P0=A'ésQ0=B' . Ekkor P1 is A', P2 A'B' felezőpontja, P3P2 és C' felezőpontja, P4 pedig P3 és D' felezőpontja. Q1 A'B' felezőpontja ( =P2) , stb . ld az ábrán.
Tovább egyszerűsíthető a szerkesztés, ha figyelembe vesszük, hogy H5 aránya 1/16, így D-t csak P0 és képei alapján is megkaphatjuk: a P0P4 szakaszt hosszabítsuk meg P4-n túl az 1/15-ével.
Szerkesztésünk helyességét igazolja ha a lépéseket számítással követjük. Tetszőleges P0-ból indulva 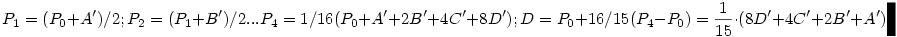 , mint azt az egyenletrendszerből kaptuk. , mint azt az egyenletrendszerből kaptuk.
b) Az AC átlóval kettévágott négyszög egyik része , az ABC  területe fele a BB'C' területe fele a BB'C'  -nek, mivel AB = BB' és C'B = 2 CB. Hasonlóan a négyszög másik része, ACD -nek, mivel AB = BB' és C'B = 2 CB. Hasonlóan a négyszög másik része, ACD  területe fele az A'DD' területe fele az A'DD'  -nek. E két -nek. E két  területe tehát együtt a négyszög területének duplája. Ugyanez igaz a BD átlóval kettévágott négyszögre és az A'B'A ill. C'D'C területe tehát együtt a négyszög területének duplája. Ugyanez igaz a BD átlóval kettévágott négyszögre és az A'B'A ill. C'D'C  -ekre. Így A'B'C'D' területe 5-szöröse az ABCD területének. -ekre. Így A'B'C'D' területe 5-szöröse az ABCD területének.
|
 |
| Előzmény: [1002] BohnerGéza, 2008-03-27 22:32:12 |
|
|
| [1002] BohnerGéza | 2008-03-27 22:32:12 |
 131. feladat: Az ABCD pozitív körüljárású négyszög minden oldalát, pozitív körüljárást tartva, meghosszabbíttottuk az oldal hosszával, kaptuk az A'B'C'D' négyszöget. ( pl. az AB' felezőpontja B )
a.) Ismerve A'B'C'D' négyszöget, szerkesztendő az ABCD!
b.) Hányszorosa az A'B'C'D' területe az ABCD területének?
|
|
| [1001] HoA | 2008-02-18 15:56:38 |
 A 130.feladat megoldása: Legyen az x, y, z szakaszok talppontja az a, b, c oldalak egyenesén rendre Ta,Tb,Tc. Merőleges szárú szögekről lévén szó, x és y bezárt szöge  vagy vagy - - , mindenesetre a PTaTb , mindenesetre a PTaTb  területe területe 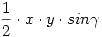 . Hasonló igaz PTbTc és PTcTa . Hasonló igaz PTbTc és PTcTa  -ekre. Kifejezésünkben, melyet jelöljünk F-fel, helyettesítsünk a=2Rsin -ekre. Kifejezésünkben, melyet jelöljünk F-fel, helyettesítsünk a=2Rsin , b=2Rsin , b=2Rsin , c=2Rsin , c=2Rsin szerint, ekkor F=2R(y.z.sin szerint, ekkor F=2R(y.z.sin +z.x.sin +z.x.sin +x.y.sin +x.y.sin ). A zárójelben a fenti ). A zárójelben a fenti  -ek előjeles területösszegének kétszerese áll. A továbbiakban azt vizsgáljuk, ez P milyen helyzetére lesz 0. -ek előjeles területösszegének kétszerese áll. A továbbiakban azt vizsgáljuk, ez P milyen helyzetére lesz 0.
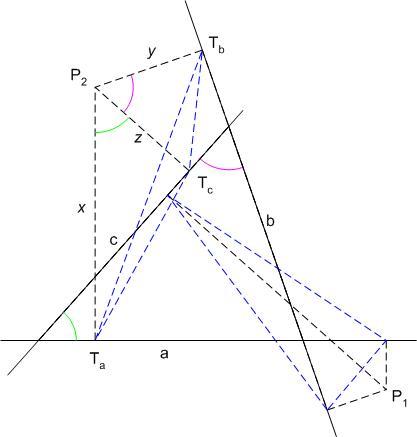
A  belsejében biztosan nem, hiszen ott mindhárom tag pozitív. A belsejében biztosan nem, hiszen ott mindhárom tag pozitív. A  3 csúcsa viszont megfelel, hiszen ott x,y,z közül kettő 0, így az összeg mindhárom tagja 0. A 3 egyenes által 7 részre vágott síknak abban a 3 részében, melyek határán csak egy hsz csúcs van, x,y,z közül 2 negatív és 1 pozitív (P1 pont) , az előjeles 3 csúcsa viszont megfelel, hiszen ott x,y,z közül kettő 0, így az összeg mindhárom tagja 0. A 3 egyenes által 7 részre vágott síknak abban a 3 részében, melyek határán csak egy hsz csúcs van, x,y,z közül 2 negatív és 1 pozitív (P1 pont) , az előjeles  területekből is így 2 negatív és 1 pozitív, de a két negatív területű területekből is így 2 negatív és 1 pozitív, de a két negatív területű  egyesítése magában foglalja a pozitív területűt, így az összeg nem lehet 0. ( Ezt persze bizonyítani kell ) . A maradék 3 síktartományban x,y,z közül 2 pozitív és 1 negatív (P2 pont), az előjeles egyesítése magában foglalja a pozitív területűt, így az összeg nem lehet 0. ( Ezt persze bizonyítani kell ) . A maradék 3 síktartományban x,y,z közül 2 pozitív és 1 negatív (P2 pont), az előjeles  területekből így 2 negatív és 1 pozitív, az előjeles összeg csakkor lesz 0, ha a területekből így 2 negatív és 1 pozitív, az előjeles összeg csakkor lesz 0, ha a  területek abszolút értékei közül kettőnek az összege megegyezik a harmadikkal. Ez pedig csakkor teljesül, ha a TaTbTc területek abszolút értékei közül kettőnek az összege megegyezik a harmadikkal. Ez pedig csakkor teljesül, ha a TaTbTc  területe 0, vagyis ha Ta,Tb,Tc egy egyenesbe esik. Mivel ezek éppen a P-ből az oldalegyenesekre bocsátott merőlegesek talppontjai, a keresett mértani hely a területe 0, vagyis ha Ta,Tb,Tc egy egyenesbe esik. Mivel ezek éppen a P-ből az oldalegyenesekre bocsátott merőlegesek talppontjai, a keresett mértani hely a  körülírt köre. körülírt köre.
UI: Itt is megkérdezem, tudja-e valaki, mi lett a sulinet.hu KöMaL archívumával?
|
 |
| Előzmény: [999] BohnerGéza, 2008-02-10 11:50:42 |
|
|
| [999] BohnerGéza | 2008-02-10 11:50:42 |
 130. feladat: Legyen a P pont előjeles távolsága az ABC háromszög oldalaegyeneseitől rendre x, y ill. z.
( Pl. x pozitív, ha BC-nek az A felöli oldalán van. )
Adjuk meg azon P-k mértani helyét, melyekre ayz + bzx + cxy = 0!
|
|
| [998] HoA | 2008-01-31 13:04:36 |
 Igen, szerintem nagyon szép "szerkesztéses" megoldás. Ha már itt tartunk, nem tudom volt-e már a fórumom - vagy máshol - a "szerkesszünk háromszöget ha adottak a magasságvonalai" feladat. És persze nem a reciprok szakaszok szerkesztésére, vagy - ha létezik - a magasságvonalakból szerkesztett háromszög magasságvonalaira, mint a szerkesztendővel hasonló háromszögre gondolok.
|
| Előzmény: [997] BohnerGéza, 2008-01-30 15:29:05 |
|
|
|
| [995] HoA | 2008-01-29 17:59:48 |
 Talán egy egylépéses meggondolás segít. Húzzuk meg a körnek a háromszög oldalaival párhuzamos érintőit. Mivel a háromszöglemez tartalmazza a kört, ezek az érintők nem alkothatnak az eredetinél nagyobb háromszöget, legfeljebb kisebbet. Ezt a második háromszöget a körrel együtt nagyítva az eredeti háromszöget és annak beírt körét kapjuk. A beírt kör tehát nem lehet kisebb eredeti körünknél.
|
| Előzmény: [994] tolgyesik, 2008-01-29 17:20:34 |
|
| [994] tolgyesik | 2008-01-29 17:20:34 |
 A körül írt kör esetén én is megtaláltam az ellenpéldát, de a beírt kör esetén még mindig bizonytalan vagyok.
|
|
| [993] HoA | 2008-01-29 10:48:47 |
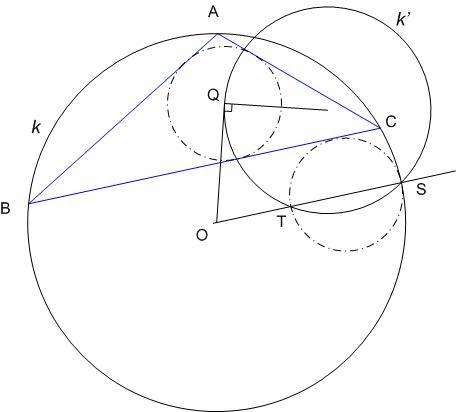
 Gondolatébresztőnek, amíg nem születik egy igazi "szerkesztéses" megoldás. Legyen adott az O középpontú, R sugarú k körvonalon az A pont, a kör belsejében a Q pont. Az Euler tétel szerint d2=R(R-2r) . Esetünkben d = OQ . Legyen az OQ-t Q-ban érintő, k-t metsző k' kör és k egyik metszéspontja S, OS és k' másik metszéspontja T. Ekkor a szelőtétel értelmében d2=OQ2=OS.OT=OS(OS-ST)=R(R-ST) . Tehát ST = 2r. A Q körüli, ST átmérőjű kör a háromszög beírt köre, a B és C csúcsokat e kör A-ból húzott érintői metszik ki k-ból.
|
 |
| Előzmény: [992] komalboy, 2008-01-26 17:23:57 |
|
| [992] komalboy | 2008-01-26 17:23:57 |
 Egy (remélem) könnyed feladat a geometriakedvelőknek: Adott egy körvonalon egy pont, és egy pont a körvonalon belül. Határozzunk meg a körvonalon másik két pontot úgy, hogy a körvonalra illeszkedő, ezen három pont alkotta háromszög beírható körének középpontja legyen az adott belső pont.
|
|
|
| [990] jonas | 2008-01-25 13:24:05 |
 A 8. viszont nem igaz általában. Hegyesszögű háromszögre a körülírt kör a legkisebb sugarú ilyen kör, tompaszögű háromszögre viszont a hosszú oldal Thales-köre az -- derékszögűre a kettő megegyezik.
|
| Előzmény: [988] tolgyesik, 2008-01-25 11:52:31 |
|
| [989] rizsesz | 2008-01-25 13:11:46 |
 7. egy olyan kör van, ami egy háromszög minden oldalát belülről érinti, ez a beírt kör. Tegyük fel, hogy találtunk egy maximális sugarú kört, ami nem érinti mind3 oldalt. Ekkor ha 2 érintési pont van, akkor azokat rögzítve a kört nagyíthatjuk, méghozzá úgy, hogy a középpontját a 2 két érintési pont szakaszfeleő merőlegesén eltoljuk. Így előbb-utóbb mindenképpen eljutunk a beírt körhöz.
|
| Előzmény: [988] tolgyesik, 2008-01-25 11:52:31 |
|
| [988] tolgyesik | 2008-01-25 11:52:31 |
 Kedves Fórumozók!
Két régi feladatról olvastam a fórumon, és felmerült bennem a kérdés, hogy ez a két állítás mégsem triviális?
7. feladat: Igaz-e, hogy a (nem elfajuló) háromszög beírt köre a legnagyobb sugarú kör, melyet a háromszöglemez tartalmaz?
8. feladat: Igaz-e, hogy a (nem elfajuló) háromszög köré írt kör a legkisebb sugarú kör, mely tartalmazza a háromszöglemezt?
|
|
| [987] Süni131 | 2008-01-23 20:48:01 |
 Kedves Fórumozók!
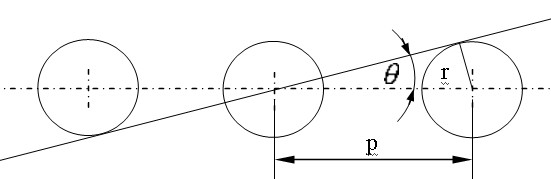
Egyező átmérőjű körök középpontjai egy egyenesen, egymástól egyenlő távolságra helyezkednek el. Hogyan tudnám meghatározni egy másik egyenesnek az előzővel bezárt minimális szögeit, ha a feltétel a következő:
az egyenes által kimetszett húrhosszúságok összege nem haladhatja meg az 1, 2,...,n körátmérőt, az egyenesnek az adott szögek alatti bárhová történő eltolása mellett.
A segítséget előre is köszönöm,
Üdv: Süni131
|
 |
|
| [986] HoA | 2008-01-21 14:03:33 |
 Konkrét irodalmat nem ismerek, de mivel eddig senki sem reagált, leírom az ötleteimet. Szerintem a feladatot a regressziós egyenes mintájára lehet kezelni. Ott adva van n db pont - (xi,yi) koordinátapár - melyek nem pontosan egy egyenesre illeszkednek és a feladat a pontokra legjobban illeszkedő y = ax + b egyenes megadása. Mint tudjuk, ha az eltérés mértékének a 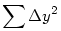 -t vesszük, ahol -t vesszük, ahol  yaz egyenes xi -beli y koordinátájának és yi -nek a különbsége, akkor az eltérés a ill b szerinti deriváltját 0-nak véve az egyenes a ás b paramétereire elsőfokú egyenletrendszert kapunk. yaz egyenes xi -beli y koordinátájának és yi -nek a különbsége, akkor az eltérés a ill b szerinti deriváltját 0-nak véve az egyenes a ás b paramétereire elsőfokú egyenletrendszert kapunk.
Egyszerűség kedvéért vegyünk először egy síkbeli példát 3 ponttal. Legyenek adva az A,B,C pontok, valamint az A*, B*, C* pontok koordinátái. Feltesszük, hogy az ABC és A*B*C* háromszögek nagyjából hasonlóak és keressük azt a transzformációt, mely ABC-t az A*B*C*-t jól közelítő A'B'C'-be viszi át. Ha AB és A'B' különböző hosszúak és nem párhuzamosak, ez egy nyújtva forgatás. Ha alakzatainkat a komplex számsíkon ábrázoljuk, a nyújtva forgatásnak egy z'=z0+wz transzformáció felel meg, - ld. Pl. Reimann István:Geometria és határterületei - és itt is az a feladat, hogy határozzuk meg a z0 és w számokat úgy, hogy az A,B,C pontok képei, A'B'C' a "legközelebb" legyenek az A* B* C* pontokhoz. A hiba mértékének talán itt is tekinthetjük az A'A* ... távolságok négyzetösszegét. Azt persze nem mondom, hogy z0-ra és w-re itt is elsőfokú egyenletrendszert kapunk, de ha máshogy nem, közelítő módszerekkel a feladat megoldható.
Térbeli transzformációnál még bonyolultabb a helyzet, de ott is megtalálható az a transzformáció, mely két hasonló alakzat egyikét a másikba átviszi (tenzor?) és ott is felírható a megadott A*, B* , ... és a transzformáció által létrehozott A', B', ... pontok távolságának négyzetösszege, illetve ennek az összegnek a transzformációs objektum paramétereitől való függése. Utána már csak néhány deriválás és egyenletrendszer megoldás van hátra..
|
| Előzmény: [983] farkasb, 2008-01-08 19:34:30 |
|
| [983] farkasb | 2008-01-08 19:34:30 |
 Tisztelt Fórumozók!
Nem egy konkrét feladatot, kérdezek, hanem csak azt, hogy ismer-e valaki olyan segédletet, anyagot, módszert, ami alapján el tudnék készíteni egy térbeli transzformációt, hogy: - adott egy térbeli alakzat elméleti alakjának koordinátái egy globális rendszerben - adott ugyanennek az alakzatnak a koordinátái egy lokális koordinátarendszerben, és a pontjai kis mértékben eltérnek az elméleti alakzattól - és ezt a lokális rednszert szeretném a globálisba transzformálni közös pontok felhasználásával úgy, hogy közben lehessen látni az ellentmondásokat, eltéréseket, hibákat, és ki lehessen venni a transzformációs paraméterek számításából azokat a pontokat, amik nagy mértékben eltérnek. Előre is köszönnettel: farkasb
|
|
|
| [981] BohnerGéza | 2008-01-06 02:29:39 |
 Érdemes tudni, hogy egy AB szakasz látókörének két íve nem teljesen egyenértékű. Ha az egyikről AB fí szögben látszik, akkor a másikról -fí-ben.
Tekintsük HoA [978] ábráját! Ott lényeges a feladat szempontjából, hogy F-ből DA és CB ugyanolyan irányítású egyforma szögben látszik, ez a DEA(=CEB) szöggel egyenlő.
|
| Előzmény: [979] HoA, 2008-01-04 15:42:37 |
|
| [984] BohnerGéza | 2008-01-06 02:15:02 |
 Köszönöm HoA!
A 129. feladat kitűzésekor valóban arra gondoltam, ha minden olyan ABCD négyszögre igaz, melyben AB nem egyenlő CD-vel, azaz valódi hasonlósággal (körüljárástartó) kaphatjuk AB-ből CD-t, akkor E a megfelelő forgatva nyújtásnsak a kp-ja, tehát a fixpontja is.
Ehhez minden lehetőségre meg kell mutatni, hogy E mindig a körök AFD ill. BFC ívén van. (Pl. akkor is, ha F az AB szakaszon van. )
Még azzal is, kell kezdeni valamit, ha a két kör érinti egymást - F-ben.
Sőt Az AB párhuzamos CD-t is vizsgálni kell. Mindezt a fórumon pontosan leírni nem érdemes - a következő hozzászólásban egy dologról még írok-, de:
Ha mindent megmutattunk, akkor bebizonyítottuk, hogy minden valódi hasonlóságnak van fixpontja. A feladat - a speciális eseteket kivéve - lehetőséget mutat a fixpont szerkesztésére.
|
| Előzmény: [977] HoA, 2008-01-04 10:43:57 |
|
| [980] Bubóka | 2008-01-04 18:36:09 |
 Igen, ezt így tudtam én is, de nem ez volt a feladat, amit nem tudtam. De azért köszi. Hidd el a másik is lehetséges, hisz az egyetemen kérik. De ha megtudom, közre adom!!
|
| Előzmény: [979] HoA, 2008-01-04 15:42:37 |
|
| [979] HoA | 2008-01-04 15:42:37 |
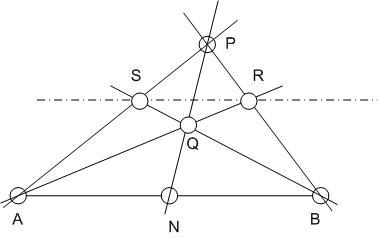
 Na látod, ez az, amiről eddig szó sem volt: adott a szakasz felezőponja is. Egy megoldás: P az AS egyenes szabadon választott pontja, PN és SB metszéspontja Q, AQ és PB metszéspontja R, SR a keresett egyenes.
Hogy "adott pontból adott pontra állítson merőlegest" azt meghagyom neked.
|
 |
| Előzmény: [978] Bubóka, 2008-01-04 13:46:22 |
|
| [978] Bubóka | 2008-01-04 13:46:22 |
 Tisztelt Fórumozók! Látom galibát okoztam, bár nem állt szándékomban. A feladatom amit nem tudok megoldani, az az volt és nem több, hogy adott pontból adott pontra állítson merőlegest. sajnos nincs itt semmiféle körkp és egyebek. Eljutottunk a párhuzamos szerkeszthetősége vonalzóval vitájához, amit konkrétan nem fejtettem ki, mert nem ez volt a feladatom, pusztán reagáltam Jónásnak arra, hogy lehetséges. De most megteszem. A feladat: adott egy AB szakasz, annak N felező pontja és S pont mely nem illeszkedik a szakaszra. Húzzon S-en át párhuzamost az AB szakasszal. Mivel a (csak)vonalzós szerkesztésekhez 4 adott pontra van szükség így egy 4. pontot tetszőlegesen veszünk föl (az A és S pontot összekötő egyenesen). HA több időm lesz megpróbálom itt megszerkeszteni de legalábbis leírni a menetét, de épp geo. vizsgára készülök.
|
|
| [977] HoA | 2008-01-04 10:43:57 |
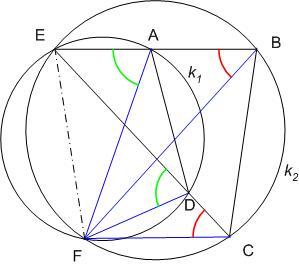
 Az ábra szerinti elrendezésben az ABF és CDF háromszögek B-nél ill. C-nél lévő szögei (piros) a k2 körben, A-nál ill. D-nél lévő külső szögei (zőld) a k1 körben az EF húrhoz tartozó kerületi szögek. Úgy vélem, BohnerGéza nem a nehézsége miatt adta fel ezt a feladatot, hanem valamilyen érdekes észrevétele van - talán a forgatva nyújtással vagy a négy háromszög tételével kapcsolatban?
|
 |
| Előzmény: [966] BohnerGéza, 2008-01-02 22:51:56 |
|
| [976] HoA | 2008-01-04 10:28:35 |
 Én meg úgy gondolom, hogy egy geometria fórumon a szerkesztési feladatokat szabatosan illik megfogalmazni. Mi adott és mit kell szerkeszteni? Ha például kiderül, hogy az egyenesen és ponton kívül még egy kör meg a középpontja is adott, akár merőlegest is szerkeszthetsz az adott ponból az adott egyenesre csak vonalzóval.
|
| Előzmény: [971] Bubóka, 2008-01-04 08:23:54 |
|
| [975] rizsesz | 2008-01-04 10:27:45 |
 Elnézést, legközelebb nem csak az egy hozzászólást nézem meg. :) Ennek így valóban előfeltétele egy és más. Bubókának drukkolok a vonalzóval szerkesztéshez!
|
| Előzmény: [974] jonas, 2008-01-04 09:29:08 |
|
| [974] jonas | 2008-01-04 09:29:08 |
 Igen, de ott meg van adva egy párhuzamos, és egy másikat kell szerkeszteni. Azt tényleg meg lehet csinálni.
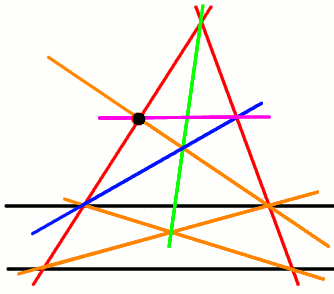
Adott a két párhuzamos fekete egyenes, és a fekete pont. Meghúzod tetszőlegesen a két piros egyenest, az egyiket a fekete ponton keresztül. Utána meghúzod a három narancssárga egyenest a megfelelő metszéspontokat összekötve, utána a zöld egyenest, majd a kéket, végül a rózsaszínt. A rózsaszín párhuzamos lesz a két feketével.
(Nem vagyok benne biztos, hogy ez a legegyszerűbb szerkesztés, lehet, hogy egy egyenest meg lehet spórolni.)
Ha viszont nincs másik párhuzamos adva, csak egy fekete egyenes és egy pont, akkor csak egyenes vonalzóval szerintem nem lehet megszerkeszteni a rózsaszín párhuzamost. A 969. hozzászólást egyszerűen nem gondoltam át.
|
 |
| Előzmény: [972] rizsesz, 2008-01-04 08:57:56 |
|
| [973] nadorp | 2008-01-04 09:20:01 |
 Az a feladat is így kezdődik: "Adott egy trapéz,...", azaz nem csak egy egyenes és egy pont adott síkon,hanem egy párhuzamos egyenespár és egy pont. Jonas épp azt kérdezte [969], hogy Bubóka eredeti feladatában nincs-e más is megadva a ponton és az egyenesen kívül.
|
| Előzmény: [972] rizsesz, 2008-01-04 08:57:56 |
|
|
| [971] Bubóka | 2008-01-04 08:23:54 |
 Elnézést lehet kérni, de lehet párhuzamost húzni vonalzóval!!!!!! Adott ponton át adott egyenesre, "trapéz feladat" segítségével! Én úgy gondolom, hogy azért mert valaki valamit nem tud az nem egyenlő azzal, hogy olyan nem létezik.
Nem tévedés volt a merőleges. Biztos hogy lehet, csak én nem jövök rá egyenlőre a menetére.
|
| Előzmény: [970] jonas, 2008-01-03 22:17:18 |
|
|
| [969] S.Ákos | 2008-01-03 21:21:58 |
 Így hirtelen nem látom, hogy párhuzamost hogy lehetne csak vonalzóval szerkeszteni. Felvilágosítanál?
Bubóka: Az 5-szög szerkesztése meg abból következik, hogy az egységnyi sugarú körbe írt 10szög oldala 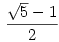 . Ez pithagorasz-tétel segítségével meg könnyen szerkeszthető. . Ez pithagorasz-tétel segítségével meg könnyen szerkeszthető.
|
| Előzmény: [968] jonas, 2008-01-03 19:31:17 |
|
| [968] jonas | 2008-01-03 19:31:17 |
 "Hogy kell pontból egyenesre merőlegest bocsátani CSAK vonalzóval?"
Nem párhuzamosra gondolsz véletlenül? Ha nem, akkor nincs valami más is adva? Mert így lehetetlen.
|
| Előzmény: [967] Bubóka, 2008-01-03 18:22:34 |
|
| [967] Bubóka | 2008-01-03 18:22:34 |
 Üdv Mindenkinek! Segítségeteket szeretném kérni. Hogy kell pontból egyenesre merőlegest bocsátani CSAK vonalzóval? HA a menetét valaki leírná, nagyon megköszönném. Ja! És szabályos ötszöget szerkeszteni az aranymetszéssel...?
|
|
| [966] BohnerGéza | 2008-01-02 22:51:56 |
 129. feladat: Az ABCD négyszög nem trapéz. AB és CD az E-ben metszik egymást. Az ADE és BCE körülírt köre E-n kívül F-ben találkoznak. Bizonyítandó, hogy ABF és CDF hasonlóak!
|
|
|
| [964] BohnerGéza | 2007-12-31 14:05:01 |
 A megkötés valóban nem kell, a kitűzők talán a 9-eseknek szóló feladatot "nehezítették", lehessen általánosítani. A korosztálytól nem feltétlenül trigonometriát használó megoldást vártak. Az elemi tetszett nekem jobban.
|
| Előzmény: [963] SmallPotato, 2007-12-30 19:30:47 |
|
| [963] SmallPotato | 2007-12-30 19:30:47 |
 A megoldás szerintem is helyes. (Pontosabban: nekem is ez jött ki. :-) )
Két hozzáfűznivalóm lenne azért:
A feladat kifejezetten hegyesszögű háromszöget ír; Te nem ilyet rajzoltál, bár elsőre nekem sem tűnik lényeginek a megkötés. (Majd lehet, hogy engem is helyreigazítanak. :-D)
A másik: a jövőre nézve szerencsésebb lenne (mivel megszokott), ha a háromszög csúcsait az óramutató járásával ellentétes sorrendben betűznéd, és a szögeket ugyanezen sorrendben osztanád ki (az A csúcsban  , a B csúcsban , a B csúcsban  stb.) stb.)
Azért merem ezt kérni, mert emlékszem első táblai geometria-szereplésemre a gimiből: nem szokványosan betűztem a háromszöget, és a padsorokból tömény húúúúúú jött ... :-)))
|
| Előzmény: [962] S.Ákos, 2007-12-30 12:06:40 |
|
|
| [961] BohnerGéza | 2007-12-30 01:01:09 |
 A komáromi Selye János Magyar Tannyelvű Gimnázium Cornides István Emlékversenyének ( 2007.12.07 ) egy szép feladatát ajánlom:
128. feladat: Az ABC hegyesszögű háromszögben az A-nál lévő szög a B-nél lévő kétszerese. A C-ben a BC-re állított merőleges AB-t D-ben metszi. Mennyi az AC / BD arány?
|
|
|
| [959] Cogito | 2007-12-14 17:02:50 |
 Kedves HoA!
A feladatot pár napja én is megoldottam, csak az idő hiányzott, hogy letisztázva közölhető állapotba hozzam. Egyetértek azzal, hogy ez a kör a keresett mértani hely abban az esetben, ha a feladatot az ABC síkra szűkítjük. A részleteket most mellőzve nekem az jött ki, hogy a mértani helynek eleget tévő P pontokra teljesül, hogy
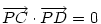 | (1) |
, ahol a C pontnak O-ra való középpontos tükörképe D. Mint látható, itt (egyrészt) azon pontok halmazáról van szó, melyekből a CD szakasz derékszög alatt látszik. Ez pedig az a C és D pontok nélküli gömbfelület, amely az Általad kapott kör CD körüli megforgatásával áll elő. Itt is igaz (másrészt) hogy a C és D pont is a mértani helyhez tartozik, hiszen a P C, vagy P C, vagy P D esetben egy-egy nullvektor miatt teljesül (1). A levezetés itt is megfordítható, tehát a teljes gömbfelület a keresett mértani hely. D esetben egy-egy nullvektor miatt teljesül (1). A levezetés itt is megfordítható, tehát a teljes gömbfelület a keresett mértani hely.
Ez az általános megoldás, hiszen a feladat szövege megengedi, hogy P-t térbeli pontnak tekintsük, a levezetés(ek) pedig ennek az értelmezésnek is eleget tesznek.
|
| Előzmény: [958] HoA, 2007-12-14 08:26:03 |
|
|
|
| [956] szegeddiák | 2007-11-28 21:32:57 |
 Sziasztok...segítségre lenne szükségem néhány feladatjoz..ha vki meg tudja oldani ezeket kérem rakja fel vagy vegye fel velem a kapcsolatot.Igazán sürgős lenne mert pénteken ebből zh-t írok.köszi előre is
tehát a feladatok: kocka élén áll ábrázolni Monge féle ábrázolással csúcsán álló , élén álló oktaéder ábrázolása monge féle ábrázolással teraéder lapján , csúcsán és élén áll szintén monge ábrázolással.
|
|
|
| [954] Hajba Károly | 2007-11-28 08:11:00 |
 Még mindig kevés az infó. A négyzet melyik egyenese az egyenes és melyik pontja a pont? Mikorra kellene? Péntekre tudnám elkészíteni a segédábrát, de majd az 'ábrázoló geometriában', oda való.
|
| Előzmény: [953] tyotyke, 2007-11-28 07:52:38 |
|
| [953] tyotyke | 2007-11-28 07:52:38 |
 Szia! Igen elhamarkodottan írtam le a dolgokat.Egy pont és egy egyenes két képéről van szó, és ebből kell egy kockát szerkesztenünk, csak a négyzetet azért irtam, mert az már 2-es és onnantól kezdve a magasságvonalak szerkesztésével a kocka csak néhány lépés. Fel kell vennünk egy első fővonalat......stb., leforgatotott háromszögből berajzoljuk a valódi kocka oldalhosszát.....Ezek lépések a szerkesztésből. Remélem igy már érthető!!!:) Köszönöm a segítséget,érdeklődést! Üdv!
|
|
| [952] HoA | 2007-11-27 18:47:11 |
 Szia! Biztos vagy te abban, hogy ez két egyenes és két pont a síkban? Nem egy ábrázoló feladatról van szó és egy pont és egy egyenes két vetületét látjuk? ( Ehhez javasolnám az "ábrázoló geometria" témakört ). És mi a feladat? Hogy kell egy (vagy két?) pontból és egyenesből négyzetet és kockát szerkeszteni? Az ábrázoló esetben el tudok képzelni olyan feladatot, hogy szerkesszünk négyzetet, melynek egyik csúcsa az adott pont, oldalegyenese/átlóegyenese az adott egyenes. Vagy szerkesszünk kockát, melynek egyik csúcsa az adott pont, egyik élének/lapátlójának/testátlójának egyenese az adott egyenes. Ezek egyike a feladat?
|
| Előzmény: [950] tyotyke, 2007-11-27 12:18:55 |
|
|
| [950] tyotyke | 2007-11-27 12:18:55 |
 Sziasztok! Végig néztem a forum hozzászólásokat és meg kell hogy állapítsam, hogy itt profik társalognak! Ebből adódóan jött az ötletem, hogy a Ti segítségeteket fogom kérni és remélem segítetek is nekünk! Egy zh feladat megoldására lennénk kiváncsiak, szerkesztővonalak ábrázolásával és némi magyarázattal.A feladat általában egy tetszőlegesen adott két egyenes és két pont a síkban, amiből először egy négyzetet, majd abból egy kockát kell szerkeszteni. Megpróbálom a kiinduló ábrát csatolni, remélem sikerül. Segítségeteket előre is köszönöm!
|
|
|
|
| [947] BohnerGéza | 2007-11-26 13:20:09 |
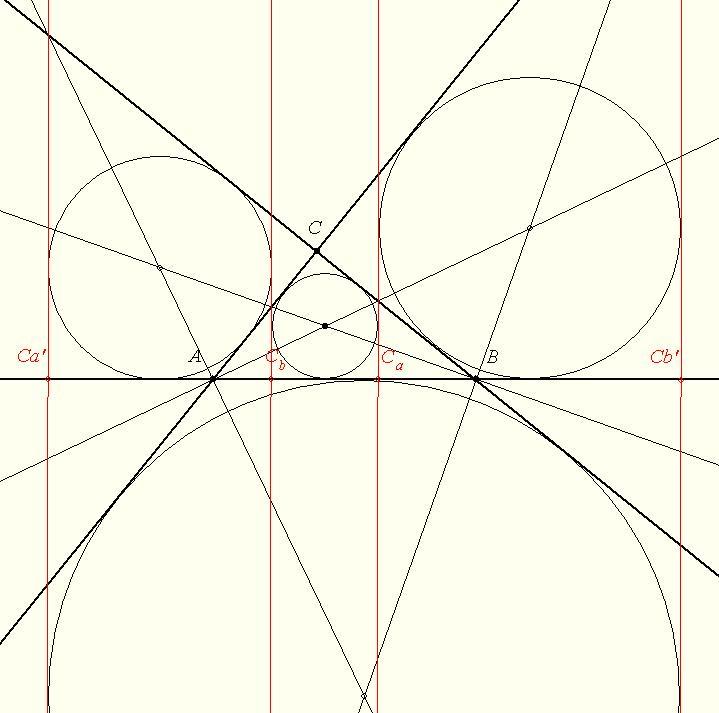
 A feladatot a következő érdekes észrevétel miatt tűztem ki:
Legyen ABC C-nél derékszögű. Tükrözzünk a C-n nem átmenő szögfelezőkre! Például Ca' a C-nek az A-hoz tartozó külső szögfelezőre való tükörképe. Ekkor AC egyenes képe AB lesz és BC képe a Ca'-n átmenő AB-re merőleges egyenes, amely érint a b és c indexű hozzáírt köröket. ....
|
 |
| Előzmény: [946] HoA, 2007-11-26 10:29:32 |
|
|
| [945] Python | 2007-11-25 12:32:17 |
 Legyenek a háromszög oldalai a, b, c, beírt körésnek sugara r, a hozzáírt körök sugara ra, rb, rc (pl. ra az a oldalhoz írt kör) ! Tegyük fel hogy pl. rc=r+ra+rb! Felhasználva hogy a t háromszögterületre 2t=r(a+b+c)=ra(-a+b+c)=rb(a-b+c)=rc(a+b-c)
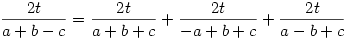
A nevezők a háromszög-egyenlőtlenség miatt pozitívak, felszorozva; 2t-vel osztva
![(a+b+c)\left[(a-b+c)(-a+b+c)+(a+b+c)(a-b+c+-a+b+c)\right]=](keplet.cgi?k=99215EE03C84BB72)
=(a+b+c)(a-b+c)(-a+b+c)
Elvégezve a műveleteket
4c(c2-b2-a2)=0
Itt 4c 0, így c2=a2+b2, és ekkor a Pithagorasz-tétel megfordítása miatt a háromszög derékszögű. 0, így c2=a2+b2, és ekkor a Pithagorasz-tétel megfordítása miatt a háromszög derékszögű.
|
| Előzmény: [943] BohnerGéza, 2007-11-22 18:21:24 |
|
|
|
|
|
| [940] HoA | 2007-11-16 16:20:18 |
 OK, helyesbítek. Tegyük fel, az adatok most már világosak. A feladat tehát így szól
1) "Bizonyítsuk be, hogy nem szerkeszthető meg a hármszög, ha adott  = = /2, ma=1 és fb=2" , illetve /2, ma=1 és fb=2" , illetve
2) "Bizonyítsuk be, hogy nem szerkeszthető meg a hármszög, ha adott a=1 , ma=1 és fb=1"
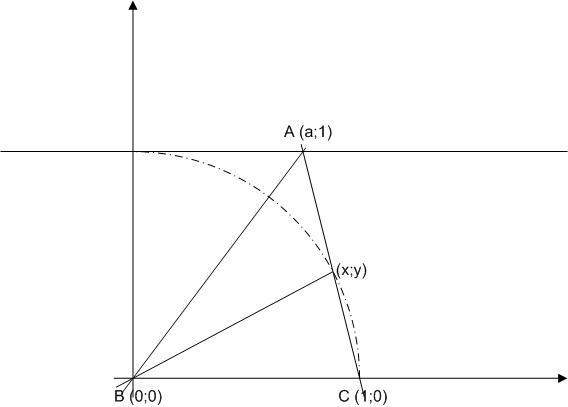
Ha így van, akkor 2) megoldásának egyik lehetséges módja: Az ábra szerint az A csúcs x koordinátájával (a) fejezzük ki x-et és y-t annak alapján, hogy
x2+y2=1 és 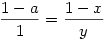
Ha jól számoltam, 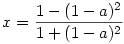 Ezután felírjuk, hogy a felezett szöggel szemközti oldalnak a szögfelező által elvágott két darabja - és így ezek x irányú vetületei is - úgy aránylanak, mint a közrezáró oldalak hossza: Ezután felírjuk, hogy a felezett szöggel szemközti oldalnak a szögfelező által elvágott két darabja - és így ezek x irányú vetületei is - úgy aránylanak, mint a közrezáró oldalak hossza:
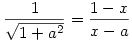 , persze x-et a-val kifejezve, kapunk a-ra egy magasabbfokú egyenletet. Erről kell (lehet?) megmutatni, hogy a megoldás nincs benne az adott adatokból szerkesztéssel elérhető számtestben. , persze x-et a-val kifejezve, kapunk a-ra egy magasabbfokú egyenletet. Erről kell (lehet?) megmutatni, hogy a megoldás nincs benne az adott adatokból szerkesztéssel elérhető számtestben.
|
 |
| Előzmény: [938] Bubóka, 2007-11-16 14:03:32 |
|
|
| [938] Bubóka | 2007-11-16 14:03:32 |
 Valószínű nem a felfogásoddal van baj! A feladat az, az amit leírtam a 935 alatt, de sajna csak ennyi:
Bizonyítsuk be, hogy az alábbi háromszögszerkesztési feladatok nem szerkeszthetők euklidészi értelemben! A harmadfokú problémáknál vizsgáljuk, hogy megoldható-e szögharmadoló eszközzel. .... és az adatok.
Nem szerkesztésről van szó. Bocsánat, de nem tudok itt egyszerű szövegen kívűl mást "szerkeszteni", ha pedig vágólapról akarok másolni, akkor nem másolja ugyanazt.
|
| Előzmény: [937] HoA, 2007-11-16 09:26:03 |
|
| [937] HoA | 2007-11-16 09:26:03 |
 Lehet, hogy kicsit nehéz a felfogásom, de nekem még így sem világos. Légy szíves írd le magyarul, mi a két feladat, valahogy így:
1) Szerkesszünk háromszöget, ha adott  = = /2, ma=1 és fb=2 /2, ma=1 és fb=2
2) Szerkesszünk háromszöget, ha adott a=1,ma=1 és fb=1
|
| Előzmény: [936] Bubóka, 2007-11-16 06:59:56 |
|
