| [1141] BohnerGéza | 2008-10-31 00:06:46 |
 A zalaegerszegi Zrínyi Miklós Gimnázium "IZSÁK IMRE GYULA" komplex természettudományi versenyének egyik szép feladatát ajánlom.
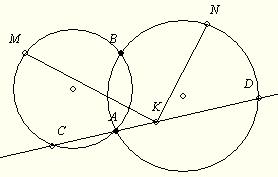
141. feladat: A k1 és k2 kör két pontban, A-ban és B-ben metszik egymást. Legyen C a k1-nek k2-n kívüli olyan pontja, melyre a CA egyenes k2-t olyan az A-tól különböző D pontban metszi, mely nincs a k1-en belül. Továbbá legyen K a CD, M a k1 A-t nem tartalmazó BC ívének és N a k2 A-t nem tartalmazó DB ívének felezőpontja. Bizonyítandó, hogy MKN szög derék!
|
 |
|
| [1140] HoA | 2008-10-26 23:06:36 |
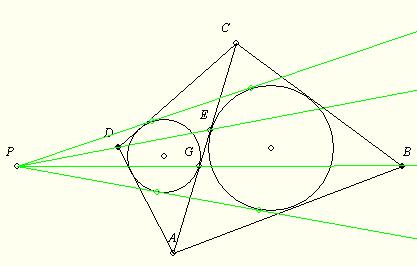
 Pedagógiailag nagyon jó feladatnak tartom. Szinte vonzza a szemet, hogy AC felezőpontját E és G között NEM jelöli az F betü. Honnan ismerős a szakaszt két oldalról érintő két kör, ráadásul az ábra alapján a szakasz felezőpontjára szimmetrikus két pontban? Először belátjuk, hogy ez nem csak ránézésre van így, hanem a [1139] - beli egyenlőség éppen a feladat feltételeiből következik. És ami még "hiányzik" az ábráról: ABC beírt k1 körének E-vel átellenes H pontja - és ugyanígy ACD beírt k2 körének G-vel átellenes I pontja , melyek úgy tűnik, rajta vannak BG-n illetve DE-n. Végül az ABC háromszög AC oldalát G-ben érintő hozzáírt k3 kört megrajzolva teljes az ábra. Így már jól láthatóak a beírt és hozzáírt körök vizsgálatánál megismert hasonlóságok. k1 és k3 külső hasonlósági pontja B, ezért B, H és G valóban egy egyenesen van. k1 és k2 külső hasonlósági pontja P, ezért P, G és H egy egyenesen van. Vagyis P, G, H, B egy egyenes pontjai. És persze ugyanez áll P, D, I, E -re.
|
| Előzmény: [1134] BohnerGéza, 2008-10-12 01:13:22 |
|
|
| [1138] HoA | 2008-10-20 08:50:44 |
 Két előzetes megjegyzés:
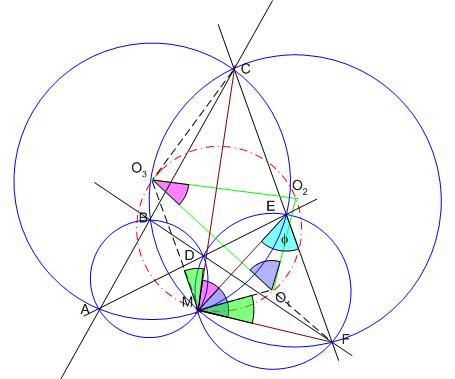
1) Nem nyilvánvaló kapcsolatot találni egy ábra bizonyos pontjain átmenő körök középpontjai és az ábra többi része között. Az itt célravezető meglátás: két egymást metsző kör centrálisa merőleges a közös húrra. Ezt a bizonyításban többször is felhasználjuk.
2) Ha sikerül bebizonyítnai, hogy tetszőleges három körülírtkör-középpont a körülírt körök közös M pontjával egy körön van, akkor egyúttal azt is bizonyítottuk, hogy a négy körülírt kör középpontja és M egy körön van, hiszen például ha O1,O2,O3ésM egy körön van , valamint O1,O2,O4ésM egy körön van, akkor ez úgy is fogalmazható, hogy O3ésO4 is rajta van az O1,O2 és M ponthármas által meghatározott körön.
[1136] ábráját megbetűzve MF merőleges O1O2 -re, ME merőleges O1O3 -ra , így nem egymás szögtartományába eső merőleges szárú szögek lévén FME =O2O1O3 =O2O1O3 . Hasonlóan adódik, hogy EMC . Hasonlóan adódik, hogy EMC =O1O3O2 =O1O3O2 . A kettőt összegezve FMC . A kettőt összegezve FMC O3O2O1 O3O2O1 kiegészítő szögével egyenlő. kiegészítő szögével egyenlő.
Jelöljük az MEF -et -et  -vel. Az O1 középpontú k1 körben ez az MF húrhoz tartozó kerületi szög. MFO1 egyenlőszárú -vel. Az O1 középpontú k1 körben ez az MF húrhoz tartozó kerületi szög. MFO1 egyenlőszárú  -ben -ben  a középponti szög, MO1F a középponti szög, MO1F fele, így FMO1 fele, így FMO1 = = /2- /2- . .
Az O3 középpontú k3 körben CEM = = - - a rövidebbik CM ívhez tartozó kerületi szög, a hosszabbik CM ívhez tartozó kerületi szög a rövidebbik CM ívhez tartozó kerületi szög, a hosszabbik CM ívhez tartozó kerületi szög  , az MCO3 egyenlőszárú , az MCO3 egyenlőszárú  -ben -ben  a középponti szög, MO3C a középponti szög, MO3C fele, így CMO3 fele, így CMO3 = = /2- /2- . .
O1MO3 =FMC =FMC -FMO1 -FMO1 +CMO3 +CMO3 =FMC =FMC , az O3O2O1 , az O3O2O1 kiegészítő szöge, tehát O1,O2,O3ésM egy körön vannak. kiegészítő szöge, tehát O1,O2,O3ésM egy körön vannak.
|
 |
| Előzmény: [1136] BohnerGéza, 2008-10-16 19:03:53 |
|
|
|
| [1135] BohnerGéza | 2008-10-12 01:28:32 |
 140/b feladat: Bizonyítandó, ha a 140. feladatban az ABCD négyszög konkáv, akkor az állítás - ha vannak - a közös belső érintőkkel, igaz! ( Szóval a BG és DE átmegy a körök belső hasonlósági pontján. )
Megjegyzés: Ha a 140-ben a két kör sugara egyforma, akkor BG és DE párhuzamos a centrálisukkal.
|
| Előzmény: [1134] BohnerGéza, 2008-10-12 01:13:22 |
|
| [1134] BohnerGéza | 2008-10-12 01:13:22 |
 140.feladat: A konvex ABCD négyszögben DA+AB=BC+CD-vel. (Nem érintőnégyszög!) Az ABC háromszög beírt köre érintse AC-t az E, a BDA-é a G pontban. Bizonyítandó, hogy a beírt körök közös külső érintői, a BG és a DE egyenesek egy ponton mennek át!
|
 |
|
| [1133] sakkmath | 2008-10-05 16:13:09 |
 Kérdéseddel dr. Dályay Pál Péterhez, a szegedi Deák Ferenc Gimnázium tanárához célszerű fordulni. A feladatot az ő javaslatára a The American Mathematical Monthly tűzte ki 2006-ban 11240-es sorszámmal. A 2008. évi februári szám internetes hivatkozása itt már a rövidített megoldást is közli.
|
| Előzmény: [1132] Lóczi Lajos, 2008-10-03 21:21:38 |
|
| [1132] Lóczi Lajos | 2008-10-03 21:21:38 |
 Az exponenciális függvény konvexitása miatt minden valós x-re 1+x ex. Speciálisan, ha x ex. Speciálisan, ha x (0,1), akkor 1-x (0,1), akkor 1-x e-x, így e-x, így 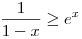 . Legyen most . Legyen most 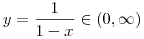 tetszőleges, ekkor tetszőleges, ekkor 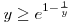 . Végezzük itt el az . Végezzük itt el az 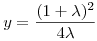 helyettesítést, ha helyettesítést, ha  >0 tetszőleges. Azt kapjuk, hogy >0 tetszőleges. Azt kapjuk, hogy 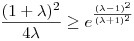 . Legyen most . Legyen most 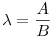 , ha A>0 és B>0 tetszőleges. Ekkor , ha A>0 és B>0 tetszőleges. Ekkor 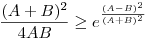 . Ha C>0 tetszőleges, akkor betűcserével ebből azt kapjuk, hogy . Ha C>0 tetszőleges, akkor betűcserével ebből azt kapjuk, hogy 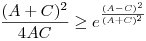 és és 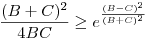 is igaz. Az utolsó három egyenlőtlenséget összeszorozva azt nyerjük, hogy minden pozitív A, B és C-re is igaz. Az utolsó három egyenlőtlenséget összeszorozva azt nyerjük, hogy minden pozitív A, B és C-re
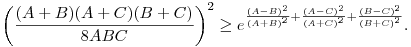
Vonjunk gyököt az egyenlőtlenségből, majd végezzük el az A=a+b-c>0, B=a-b+c>0, C=-a+b+c>0 helyettesítéseket, ahol a, b és c a háromszög oldalai. Azt kapjuk, hogy
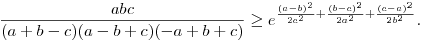
A fenti bal oldal viszont éppen 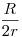 . .
Amúgy honnan jött ez az állítás? (Valami hiperbolikus/abszolút geometriai tétel?)
|
| Előzmény: [1131] sakkmath, 2008-10-03 13:36:48 |
|
|
| [1130] Káli gúla | 2008-10-01 16:36:48 |
 Ha K a a háromszög symmediáns pontja és O a köré írt kör középpontja, akkor a Tucker körök középpontjai éppen az OK szakasz pontjai. A bizonyítás megtalálható pl. W. Mclelland: A Treatise On The Geometry Of The Circle. Macmillan, 1891. könyvében a 73. oldalon. A könyv olvasható, és le is tölthető a www.archive.org oldalon, csak rá kell keresni a címére.
|
| Előzmény: [1128] klerox, 2008-09-30 17:45:13 |
|
|
| [1128] klerox | 2008-09-30 17:45:13 |
 A Tucker körnek a lényege: Feltétel: A'A"=B'B"=C'C", és A'A", B'B" és a C'C" antiparallel a BC, CA és AB oldalakkal. A hat pont: A', A", B', B", C' és C" egy körön helyezkedik el. Tudomásom szerint kell középpontjának lenni.
|
|
| [1127] BohnerGéza | 2008-09-29 22:40:25 |
 Biztos, hogy nem a "Matematikus-fizikus viccek, sztorik" közé akartad írni?
Utána néztem, a Tucker-kör vszleg hatszög, azaz önmagába visszatérő vonal. Ilyet a talpponti háromszög (piros) segítségével is meg lehet szerkeszteni. Az ábrán kettő látszik (kék, zöld) és nyilván végtelensok van. Mivel ezen hatszögek köré írható kör, de ezek kp-jai nem esnek egybe, nincs értelme a kérdésnek.
|
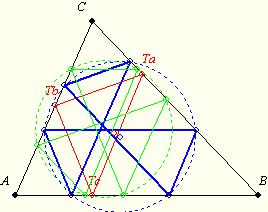 |
| Előzmény: [1126] klerox, 2008-09-29 19:30:34 |
|
| [1126] klerox | 2008-09-29 19:30:34 |
 Sziasztok!
A Tucker-kör megszerkesztésével bajlódok, de sehogy nem jövök rá a középpont megszerkesztésére, kérlek segítsetek.
Előre is köszönöm
|
|
| [1125] BohnerGéza | 2008-09-24 11:16:44 |
 Ismert a következő: Ha négy egyenes négy háromszöget határoz meg, akkor ezek körülírt körei átmennek egy közös ponton.
138. feladat: Bizonyítandó, hogy a négy körülírt kör középpontja és ez a közös pont egy körön van.
|
|
|
| [1122] Sirpi | 2008-09-08 13:41:42 |
 Nemrég nekem is szükségem volt hasonló programra, csak éppen gömbközéppontot kellett keresni felületi pontok alapján, és írtam egy egyszerű módszert, ami a tesztek alapján elég jól működik, röviden le is írom, hogyan (körre is jó változtatás nélkül):
Legyenek adva a P1,P2,...,Pn pontjaink, és keressük az O középpontot iterációs módszerrel. Legyen O0 a megadott Pi ponthalmaz súlypontja. Ha egyenletes a ponteloszlás, akkor ez már önmagában is majdnem jó, de ha nem, akkor is egy jó kiindulópont.
Nézzük a k+1. lépést: rendezzük sorba a Pi pontokat az Ok-tól vett távolság alapján, és a robusztusság miatt ebből hagyjuk el a legközelebbi és a legtávolabbi 10%-ot, legyen ez első meghagyott pont R (tehát ez egy majdnem legközelebbi pont Ok-hoz képest), az utolsó S (ez pedig a majdnem legtávolabbi, leszámítva a felső 10%-ot). Ideális esetben Ok-t az RS szakasz felezőmerőlegesére kellene "ráhúzni", de tapasztalataim alapján így lassabb a konvergencia, mintha csak a felezőmerőlegeshez képest a felére csökkentenénk a távolságot. Tehát ha Ok talppontja RS felezőmerőlegesére T, akkor Ok+1-nek válasszuk Ok és T felezőpontját, majd folytassuk az eljárást.
Megállási feltétel: Egy adott Ok pont jóságát mérjük az |SOk|-|ROk| különbséggel, és ha ez kisebb, mint az eddigi legjobb, akkor jegyezzük meg ezt, mint lehetséges végső kör/gömbközéppontot. És ha mondjuk 1000 iterációs lépésen keresztül ez a rekord nem dől meg, akkor legyen ez a végső győztes is egyben.
|
| Előzmény: [1121] farkasb, 2008-09-08 00:49:03 |
|
| [1121] farkasb | 2008-09-08 00:49:03 |
 Kedves "Fálesz" Mihály!
Visszatérve a legjobban illeszkedő körhöz... Sajnos nem tudom végigszámolni a kör a megadott segédletek alapján, elakadok vele..Az a baj,hogy nem teljesen látom át. Örülnék ha egy konkrét példán bemutatott feladatmegoldást láthatnék.
Van egy programom, ami képes erre a legjobban illeszkedő kör készítésére, a megadott pontokra az alábbi eredmények számolja:
Adottak az alábbi pontok (X,Y):
(0,1000); (10,1000); (400,4000); (500,2000); (-500,-1500); (-900,-3500); (-7000,-3500);
Eredmények(origó,sugár):
X0= -4853.3 ; Y0= 1209.7 ; R= 5352.6 ;
Távolságok az origótól:
1=4857.8; 2=4867.8; 3=5948.4; 4=5411.3; 5=5127.7; 6=6149.0; 7=5175.8;
Amennyiben nem túl nagy munka a segítség, megköszönném. Ha nagy, akkor sincs semmi gond :) Előre is köszönettel: farkasb
|
| Előzmény: [1111] Fálesz Mihály, 2008-09-02 21:45:36 |
|
| [1120] Sirpi | 2008-09-07 11:22:30 |
 Mivel semmi más adat nincs megadva a két egyenesen kívül, ezért nem nagyon jutott eszembe más lehetöség, hogy mi lehet a feladat. Felsoroltam azt a 2-t, ami viszont igen :-)
|
| Előzmény: [1118] jonas, 2008-09-03 22:25:25 |
|
|
|
| [1117] jonas | 2008-09-03 22:25:02 |
 Azt kell tudni hozzá, hogy számolhatod ki egy pontnak egy egyenestől mért távolságát. Ezután csak veszel egy pontot az egyik egyenesről, és kiszámolod ennek a távolságát a másiktól.
|
| Előzmény: [1116] Lowosan, 2008-09-03 19:41:43 |
|
| [1116] Lowosan | 2008-09-03 19:41:43 |
 távolságuk kell elfelejtettem odairni
|
|
|
|
| [1113] Lowosan | 2008-09-03 15:30:33 |
 Helló Segitségre lenne szükségem a kordinátageometria területén e:3x+2y=12 f:6x+4y=-12 ezt hogy kéne megoldani? mert új matektanárunk van és nem magyaráz semmit csak annyit mond csináljunk meg semmi más
|
|
| [1112] farkasb | 2008-09-03 13:16:31 |
 Kedves Mihály!
Köszönöm a gyors választ, megpróbálkozok a feladattal. Esetleg nem tudna ajánlani valami jó megoldást legjobban illeszkedő sík elkészítésére? A hibák az x y és z koordinátákat is terheljék. Köszönöm!
|
| Előzmény: [1111] Fálesz Mihály, 2008-09-02 21:45:36 |
|
| [1111] Fálesz Mihály | 2008-09-02 21:45:36 |
 Vaughan Pratt munkája nyomán a következőt tudom ajánlani. (Én magam is sokszor haszáltam ezt a módszert kör, gömb és henger illesztésére.)
Keressük a kör egyenletét
| f(x,y)=A(x2+y2)+Bx+Cy+D=0 | (1) |
alakban, ahol
Egy kis számolás után látható, hogy a (2) feltétel azzal ekvivalens, hogy a kör sugara 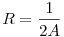 , illetve az f(x,y) függvény gradiense a körvonalon egységnyi hosszú. , illetve az f(x,y) függvény gradiense a körvonalon egységnyi hosszú.
Ha (x,y) egy pont a körvonalhoz közel, akkor |f(x,y)| jól közelíti a pont és a körvonal távolságát.
Legyenek a mintapontok (x1,y1),...,(xn,yn). Az illesztés négyzetes hibája közelítőleg
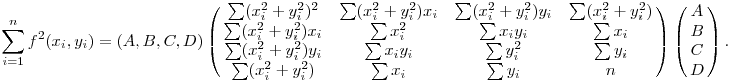 | (3) |
Szóval a (3) kifejezés minimumát keressük a (2) feltétel mellett. Ha ráereszted a Lagrange-multiplikátor módszert, kapsz egy 4-dimenziós sajátértékfeladatot, ráadásul a keresett sajátérték pont a hiba konstansszorosa...
Ha a (2) helyett az A=1 feltételt használod, akkor a számolás sokkal egyszerűbb, mert csak lineáris egyenletszert kell megoldani. Ennek a gyengéje, hogy a (3)-ban a hibát megszoroztad kb. 4R2-tel. Zajos adat esetén nagyobb lesz az illesztés valódi hibája, de kisebb lesz a sugár, amivel megszorzod.
|
| Előzmény: [1110] farkasb, 2008-09-02 09:00:28 |
|
| [1110] farkasb | 2008-09-02 09:00:28 |
 Kedves Fórumozók!
Ismételten egy kérdést tennék fel:
Hogyan határozható meg egy olyan kör középpontja, ami n számú xy koordinátával adott pontra legjobban illeszkedik? Előre is köszönettel: farkasb
|
|
| [1109] BohnerGéza | 2008-09-02 01:25:18 |
 Fálesz Mihály a [1105]-ban fölvetette, hogy egy számolás nélküli megoldás szép lenne. Egyelőre nincs hozzá ötletem. A 137/b és 137/c feladat tulajdonképpen megoldása a 137-nek, igaz végig kell gondolni. (Számolással egyszerűbben is megy [1106].)
|
 |
| Előzmény: [1108] BohnerGéza, 2008-08-28 23:51:38 |
|
|
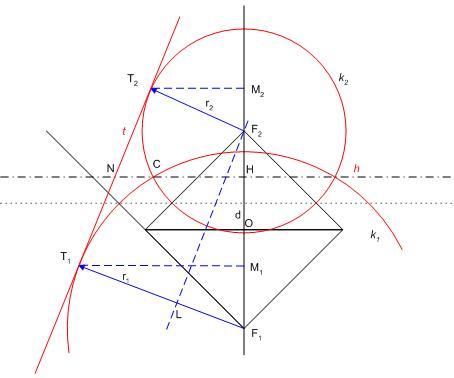
| [1107] HoA | 2008-08-28 17:10:45 |
 Még tart a nyári szünet... 137/b feladat megoldása: Legyen az F1F2 távolság 2f , F1F2 felezőpontja O. Az F1 középpontú r1 sugarú k1 és az F2 középpontú r2<r1 sugarú k2 körök h hatványvonala messe F1F2-t H -ban. Határozzuk meg az OH távolságot f,r1ésr2 ismeretében. Legyen k1ésk2 közös érintője t , az érintési pontok T1ésT2 , a Ti -ből F1F2 -re bocsátott merőleges talppontja Mi , az F2-n át t-vel húzott párhuzamos és F1T1 metszéspontja L, t és h metszéspontja N. F1L=r1-r2 Az F1M1T1,F2M2T2ésF1LF2 derékszögű háromszögek hasonlóak, 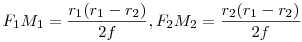 . . 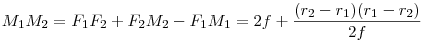 . .
N felezi T1T2 -t ( egyenlő érintőszakaszok ) , ezért H is felezi M1M2-t. 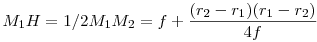 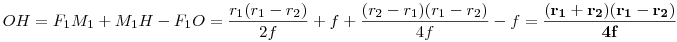 . Feladatunkban . Feladatunkban 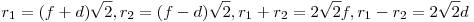 , igy , igy 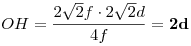 . .
|
 |
| Előzmény: [1106] BohnerGéza, 2008-08-24 23:37:33 |
|
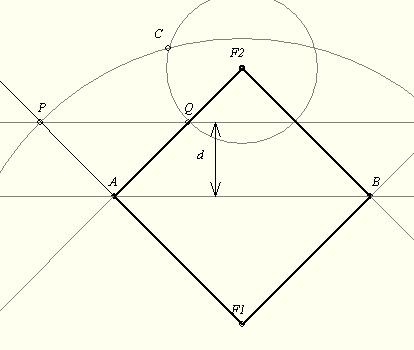
| [1106] BohnerGéza | 2008-08-24 23:37:33 |
 Tetszik az affinításos és a többi megoldás is.
Így a 137. feladat általánosításával - miszerint a középvonal 1:1 aránya helyett más arányban osztó szakaszt adunk meg a magasságpont számára - kapott feladat is könnyen bizonyítható.
Érdemes persze Fálesz Mihály ajánlata alapján, igaz számolással, az ellipszis definíciója alapján is elvégezni a bizonyítást!
137/b. feladat: Az A, F1, B, F2 pontok egy négyzet csücsai. Az AC átlóval párhuzamos - tőle d (<>0) távolságra húzott egyenes messe az AF1-t P, az AF2-t Q-ban. Legyen C az F1 kp-ú P-n és az F2 kp-ú Q-n átmenő kör kp-ja. Mutassuk meg, hogy C 2d távolságra van AC-től! (Milyen d esetén vam C pont?)
|
 |
| Előzmény: [1105] Fálesz Mihály, 2008-08-18 10:54:25 |
|
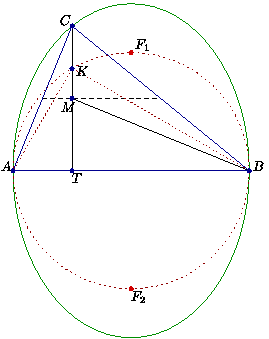
| [1105] Fálesz Mihály | 2008-08-18 10:54:25 |
 Legyen M a magasságpont, és T a C-ből induló magasság talppontja. Mint jól ismert, TC . TM = - TA . TB. (Ez azért igaz, mert a magasságpontnak az AB oldalra vonatkozó tükörképe a körülírt körön van, de például az ATC és MTB háromszögek hasonlóságából is láthatjuk.)
Ha az M pont a középvonalon van, akkor TC és TM azonos irányú, TA és TB pedig ellentétes írányú, vagyis T az AB szakasz belsejében van. A TC félegyenes tehát metszi az AB átmérőjű kört; legyen K a metszéspontjuk.
Fálesz Mihály tétele szerint BKA =90o, a magasságtételből pedig TK2=AT . TB. =90o, a magasságtételből pedig TK2=AT . TB.
Így tehát TC2=2.TC.TM=2.TA.TB=2.TK2 és
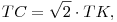
a C csűcs azon az ellipszisen van, amit az AB átmérőjű körből kapunk az AB tengelyű, 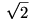 arányú merőleges affinitással. arányú merőleges affinitással.
Az A és B pont kivételével az ellipszis bármelyik pontjából kiindulva a gondolatmenet megfordítható.
* * *
Eleminek ezt a megoldást sem nevezném, bár az eredmény alapján nehéz ennél "elemibbet" várni. Aki akarja, megpróbálhatja -- számolás nélkül!!! -- bebizonyítani, hogy F1C+F2C=F1A+F2A, csak ezzel meg az a bajom, hogy az eredményt valahonnan máshonnan tudtuk meg.
|
 |
| Előzmény: [1104] HoA, 2008-08-15 15:20:47 |
|
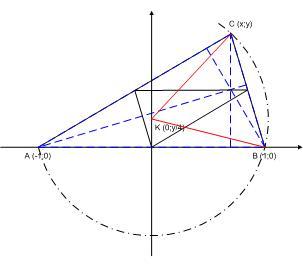
| [1104] HoA | 2008-08-15 15:20:47 |
 Ne feledkezzünk meg a 137. feladatról. Kedvcsinálónak BohnerGéza sejtésének igazolása. Ha a magasságpont az FaFb középvonalon van, akkor a körülírt kör K középpontja a középponti háromszög középvonalán van, tehát K távolsága a c oldaltól negyede mcnek. Az általánosság megszorítása nélkül legyenek A, B és C koordinátái (-1;0) , (1;0) és (x,y) . Ekkor K =(0;y/4) . KB = KC -ből a távolságok négyzetére
1+(y/4)2=x2+(3y/4)2
. 1+y2/16=x2+9y2/16 ; 1=x2+8y2/16

A C pontok egy ellipszisen helyezkednek el. Várjuk az elemi geometriai megoldásokat!
|
 |
| Előzmény: [1085] BohnerGéza, 2008-07-20 21:50:08 |
|
|
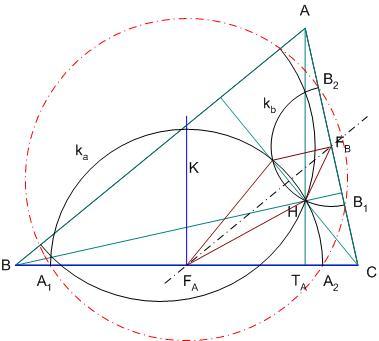
| [1102] HoA | 2008-08-12 16:42:59 |
 Köszönöm, kitűnő gondolat. Pedig már az ábrán is látszott... Mivel ka és kb egyik metszéspontja H, hatványvonaluk a H-n áthaladó, FAFB-re merőleges egyenes, vagyis mc. C rajta van a hatványvonalon, CA1.CA2=CB1.CB2, vagyis A1,A2,B1,B2 egy körön van.
|
 |
| Előzmény: [1100] Fálesz Mihály, 2008-08-12 09:22:15 |
|
|
|
| [1098] Káli gúla | 2008-08-11 21:23:53 |
 A 9-es szorzót trigonometria nélkül is megkaphatjuk: Ha a,b,c három egységvektor, azaz |a|=|b|=|c|=1, akkor
(a-b)2+(a-c)2+(b-c)2=2(a2+b2+c2)-2ab-2ac-2bc=3(a2+b2+c2)-(a+b+c)2=9-(a+b+c)2 9 . 9 .
Egyenlőség pontosan akkor van, ha a+b+c=0. Ugyanígy, n darab egységvektor közötti összes távolság négyzetösszege legfeljebb n2 (és egyenlőség csak 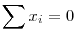 esetén lehet): esetén lehet):
![\sum_{i<j} (x_i-x_j)^2 =
\sum_{i<j} (x_i^2 + x_j^2) - \sum_{i<j} 2 x_i x_j
= (n-1) \sum x_i^2 - \left[(\sum x_i)^2 - \sum x_i^2\right]=
n^2 - (\sum x_i)^2 \le n^2](keplet.cgi?k=5E235FB51CBD26E2)
|
| Előzmény: [1093] BohnerGéza, 2008-08-05 20:34:02 |
|
|
| [1096] HoA | 2008-08-08 12:06:40 |
 [1096] - hoz hasonlóan a cosinus tételből kiindulva kicsit körülményesebben is erre az eredményre juthatunk :-) . Az adott körbe írt H0 háromszögben, mint [1096] ábráján is , legyen  a nagyságra középső szög, a nagyságra középső szög,      . Ekkor . Ekkor 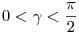 . Rögzítsük c-t , és így . Rögzítsük c-t , és így  -t is . a2+b2+c2=2.c2+2abcos -t is . a2+b2+c2=2.c2+2abcos . Ez cos . Ez cos >0 miatt annál nagyobb, minél nagyobb az ab szorzat. A sinus tételből >0 miatt annál nagyobb, minél nagyobb az ab szorzat. A sinus tételből 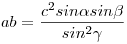 , tehát elég sin , tehát elég sin sin sin változását vizsgálni. A szorzatot összeggé alakítva sin változását vizsgálni. A szorzatot összeggé alakítva sin sin sin =1/2{cos( =1/2{cos( - - )-cos( )-cos( + + )} . Állandó )} . Állandó  mellett mellett  + + is állandó, a két szög különbségének cosinusa pedig annál nagyobb, minél kisebb a két szög különbsége. Eljutottunk [1096] eredményéhez: C -t a körülírt körön az AB ív F felezőpontja felé mozgatva is állandó, a két szög különbségének cosinusa pedig annál nagyobb, minél kisebb a két szög különbsége. Eljutottunk [1096] eredményéhez: C -t a körülírt körön az AB ív F felezőpontja felé mozgatva  - - csökken és így az oldalak négyzetösszege nő. csökken és így az oldalak négyzetösszege nő.
Mindkét megközelítésre vonatkozó megjegyzés: Szigorúan véve csak azt mutattuk meg, hogy ha van az oldalak négyzetösszegének maximuma, az csak a szabályos hármszögben lehet. Kis finomítással bizonyítható a maximum létezése. H0-ban  >60o és >60o és  <60o , mint a háromszög legnagyobb ill. legkisebb szöge. Ha C -vel F -be jutunk, a másik két szög egyenlő lesz, tehát áthaladtunk egy olyan C' pozíción, ahol a két szög egyike éppen 60o . Legyen ez a háromszög H1 . H1 -ben tehát az oldalak négyzetösszege nagyobb, mint H0-ban. Betűzzük át H1 csúcsait úgy, hogy itt is teljesüljön <60o , mint a háromszög legnagyobb ill. legkisebb szöge. Ha C -vel F -be jutunk, a másik két szög egyenlő lesz, tehát áthaladtunk egy olyan C' pozíción, ahol a két szög egyike éppen 60o . Legyen ez a háromszög H1 . H1 -ben tehát az oldalak négyzetösszege nagyobb, mint H0-ban. Betűzzük át H1 csúcsait úgy, hogy itt is teljesüljön      . Nyilván . Nyilván  lesz a 60o -os szög. H1 -ben c-t rögzítve és C -vel a körülírt körön mozogva az oldalak négyzetösszege az AB ív F felezőpontjában nagyobb lesz, mint H1 -ben . Ez a H2 háromszög viszont szabályos, hiszen lesz a 60o -os szög. H1 -ben c-t rögzítve és C -vel a körülírt körön mozogva az oldalak négyzetösszege az AB ív F felezőpontjában nagyobb lesz, mint H1 -ben . Ez a H2 háromszög viszont szabályos, hiszen  =60o és =60o és  = = . Tehát tetszőleges H0-ból indulva a szabályos H2 -ben nagyobb az oldalak négyzetösszege , mint H0-ban , H2 tényleg a maximumot adja. . Tehát tetszőleges H0-ból indulva a szabályos H2 -ben nagyobb az oldalak négyzetösszege , mint H0-ban , H2 tényleg a maximumot adja.
Második megjegyzés: [1096] helyes ábrájához a szövegben is meg kell említeni, hogy  -nak az egyik hegyesszöget választjuk. Ellenkező esetben nagyobb területhez kisebb (tompaszög) vagy változatlan (derékszög) oldal-négyzetösszeg tartozik. -nak az egyik hegyesszöget választjuk. Ellenkező esetben nagyobb területhez kisebb (tompaszög) vagy változatlan (derékszög) oldal-négyzetösszeg tartozik.
|
| Előzmény: [1095] BohnerGéza, 2008-08-08 01:43:50 |
|
|
|
|
| [1099] HoA | 2008-08-05 11:27:07 |
 Hát ha senkit nem érdekel... A [1087] feladat megoldása: Mivel A1A2 a keresett kör húrja, ennek felező merőlegese egyben a BC oldal felező merőlegese, tehát átmegy K-n, és ez a másik két oldalra is igaz, így ha van ilyen kör, annak középpontja csak K lehet. A javasolt segítséget felhasználva - legyen a helyvektorok kezdőpontja K - írjuk fel K és A2 távolságát, felhasználva, hogy ekkor  . Legyen BC felezőpontja . Legyen BC felezőpontja 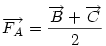 , , 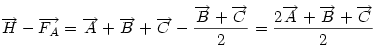 . Ennek hossza FA és A2 távolsága , ezért . Ennek hossza FA és A2 távolsága , ezért
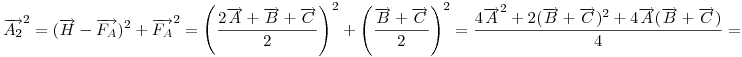

Ez a kifejezés A, B, C -ben szimmetrikus, tehát például K és B2 távolságának négyzetére ugyanezt kapnánk, a hat pont így egy K középpontú körön fekszik.
Hasonló, de trigonometriai átalakításokat igénylő megoldást kapunk, ha a feltételezett Rh körsugarat a körülírt kör R sugarával és a  szögeivel fejezzük ki. Legyen BC felezőpontja FA, ma talppontja TA . Rh2=KFA2+FAA22=KFA2+FAH2=KFA2+FATA2+TAH2 . szögeivel fejezzük ki. Legyen BC felezőpontja FA, ma talppontja TA . Rh2=KFA2+FAA22=KFA2+FAH2=KFA2+FATA2+TAH2 .
Itt KFA=R.cos , ,
BTA=2.R.sin cos cos , FATA=2.R.sin , FATA=2.R.sin cos cos -R.sin -R.sin , ,
TAH=2.R.sin cos cos .ctg .ctg =2.R.cos =2.R.cos .cos .cos . A négyzetösszeg: . A négyzetösszeg:
Rh2=R2(cos2 +4.cos2 +4.cos2 .sin2 .sin2 +sin2 +sin2 -4.sin -4.sin cos cos sin sin +4.cos2 +4.cos2 cos2 cos2 )=R2(1+4.cos2 )=R2(1+4.cos2 -4.sin -4.sin cos cos sin sin )=R2(1+4.cos )=R2(1+4.cos (cos (cos -sin -sin sin sin ))=R2(1+4.cos ))=R2(1+4.cos (-cos( (-cos( + + )-sin )-sin sin sin ))=R2(1+4.cos ))=R2(1+4.cos (sin (sin sin sin -cos -cos cos cos -sin -sin sin sin ))=R2(1-4.cos ))=R2(1-4.cos cos cos cos cos ) )
Mivel a kifejezés  , , , , -ban szimmetrikus, az első megoldáshoz hasonlóan adódik, hogy a 6 pont valóban egy K középpontú Rh sugarú körön fekszik. -ban szimmetrikus, az első megoldáshoz hasonlóan adódik, hogy a 6 pont valóban egy K középpontú Rh sugarú körön fekszik.
|
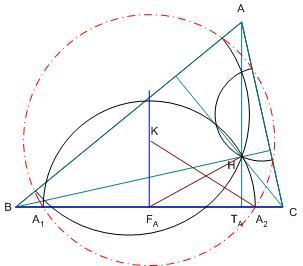 |
| Előzmény: [1087] BohnerGéza, 2008-07-22 01:24:34 |
|
| [1092] HoA | 2008-07-23 13:35:46 |
 A 136. feladat megoldása: Induljunk ki a 120o -nál nem nagyobb szögű  esetére ismert bizonyítás ábrájából. Forgassuk el a CAP esetére ismert bizonyítás ábrájából. Forgassuk el a CAP  -et az óramutató járásának irányába C körül 60o -kal, a másik két csúcs elforgatottja A' ill. P' . AA'C és PP'C -et az óramutató járásának irányába C körül 60o -kal, a másik két csúcs elforgatottja A' ill. P' . AA'C és PP'C  -ek szabályosak, AA' = AC és PP' = PC, valamint A'P' = AP , tehát azt kell igazolnunk, hogy a BPP'A' T2 törtvonal nem rövidebb a BAA' T1 törtvonalnál. Az összehasonlításnál a nehézséget csak az jelenti, hogy a két törtvonal - mint ábránkon is - keresztezheti egymást. Egészítsük ki ezért az A'P'P -ek szabályosak, AA' = AC és PP' = PC, valamint A'P' = AP , tehát azt kell igazolnunk, hogy a BPP'A' T2 törtvonal nem rövidebb a BAA' T1 törtvonalnál. Az összehasonlításnál a nehézséget csak az jelenti, hogy a két törtvonal - mint ábránkon is - keresztezheti egymást. Egészítsük ki ezért az A'P'P  -et a PA' átlójú A'P'PP'' parallelogrammává. Ekkor PP'' = P'A' és P''A' = PP', így T2 helyett vehetjük a vele azonos hosszúságú BPP''A' T3 törtvonalat. A'P' AP 60o-os elforgatottja, így a vele egyállású P''P PA-val 60o-os szöget zár be, APP'' -et a PA' átlójú A'P'PP'' parallelogrammává. Ekkor PP'' = P'A' és P''A' = PP', így T2 helyett vehetjük a vele azonos hosszúságú BPP''A' T3 törtvonalat. A'P' AP 60o-os elforgatottja, így a vele egyállású P''P PA-val 60o-os szöget zár be, APP''  szabályos, AP'' AP 60o-os órajárással ellentétes elforgatottja. Mivel AP az ABC szabályos, AP'' AP 60o-os órajárással ellentétes elforgatottja. Mivel AP az ABC  belsejében, és így a konvex BAC szögtartomány belsejében ( vagy határán ) fekszik, AP'' a BAA' konkáv szögtartomány belsejében ( vagy határán ) fekszik, ezért az APP'' belsejében, és így a konvex BAC szögtartomány belsejében ( vagy határán ) fekszik, AP'' a BAA' konkáv szögtartomány belsejében ( vagy határán ) fekszik, ezért az APP''  és így T3, a BPP''A' törtvonal is a a BAA' konkáv szögtartományba esik, P vagy P'' esetleg a határára. Legyen az AA' egyenes és T3 metszéspontja D. Jelöljük X és Y pontok T3 mentén mért távolságát tXY-nal. Ekkor tBD+DA és így T3, a BPP''A' törtvonal is a a BAA' konkáv szögtartományba esik, P vagy P'' esetleg a határára. Legyen az AA' egyenes és T3 metszéspontja D. Jelöljük X és Y pontok T3 mentén mért távolságát tXY-nal. Ekkor tBD+DA BA és tDA' BA és tDA' DA'=DA+AA' . A kettőt összeadva DA kiesik: tBD+tDA'=tBA' DA'=DA+AA' . A kettőt összeadva DA kiesik: tBD+tDA'=tBA' BA+AA', és egyenlőség csak akkor áll fenn, ha mindkét egyenlőtlenségben fennáll, vagyis ha P = P'' = A. BA+AA', és egyenlőség csak akkor áll fenn, ha mindkét egyenlőtlenségben fennáll, vagyis ha P = P'' = A.
|
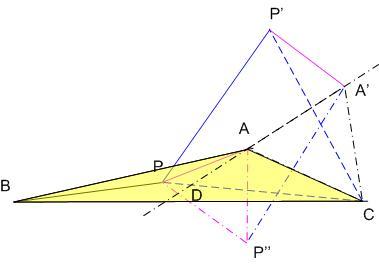 |
| Előzmény: [1078] BohnerGéza, 2008-07-15 17:42:46 |
|
|
| [1090] BohnerGéza | 2008-07-22 21:37:40 |
 Kedves farkasb!
Nekem (-17;12;1) jött ki normálvektornak.
Természetesen örülök, hogy matekkal foglalkozol. Viszont "a normálvektor" kifejezés nem jó! Egy normálvektort nullától különböző számmal szorozva szintén azt kapunk.
( normálvektorod amúgy jó )
|
| Előzmény: [1088] farkasb, 2008-07-22 18:39:20 |
|
|
| [1088] farkasb | 2008-07-22 18:39:20 |
 Kedves Fórumozók!
Lenne egy elvileg egyszerű kérdésem, nekem nem megy...nem találtam rá sehol megoldást, pedig tényleg egy alapfeladat. Adott egy sík 3 pontjával: A(1,-1,2) B(4,3,5) C(3,2,0)
Melyből a normálvektor:
n(-0.816,0.576,0.048)
És egy P(8,5,1) pont
Keresett a P pont síkon lévő merőleges vetületének xyz koordinátája.
Előre is köszönettel a segítségért: Balázs
|
|
|
|
| [1085] BohnerGéza | 2008-07-20 21:50:08 |
 ( Olyan jellegű, mint érintő négyszög esetén.)
Az alábbi feladatban, azt hiszem, másodrendű görbe a megoldás.
137. feladat: Adott az A és B pont. Határozd meg azon C pontok halmazát, melyekre az ABC háromszög magasságpontja az FaFb középvonalon van.
|
| Előzmény: [1084] m2mm, 2008-07-19 11:02:32 |
|
| [1084] m2mm | 2008-07-19 11:02:32 |
 Köszönöm a választ, de mi P pont mértani helye akkor, ha nem érintőnégyszögről van szó, hanem húrnégyszögről(ennél találtam én is jó pontokat, például a köréírt kör középpontja, és az AB és CD egyenesek metszéspontja)?
|
| Előzmény: [1083] BohnerGéza, 2008-07-19 02:14:25 |
|
| [1083] BohnerGéza | 2008-07-19 02:14:25 |
 Legyen q= PA/PD = PC/PB. Ez azt jelenti, hogy az AD és a CB szakasz q arányú Appolonius-köre a P pontban metszik egymást.
Euklides-ben felvéve egy változtatható arányt (egy állandó szakaszt és "futópont" segítségével egy változó hosszút), megszerkesztve a két szakasz ilyen arányú Appolonius-körét, ezek metszéspontjának nyomvonala kirajzolható. (Sajnos az adatokkal játszani kell, hogy valóban elég hosszú részletét láthassuk.)
Játszadozásom azt valószínűsíti, hogy általában nem másodrendű görbe vonala a keresett halmaz.
|
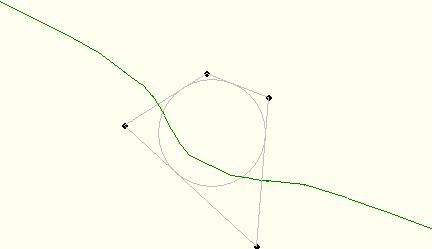 |
| Előzmény: [1079] m2mm, 2008-07-15 19:12:47 |
|
|
| [1081] HoA | 2008-07-16 13:28:18 |
 És ha igen, akkor skalár vagy vektor szorzat? A vektor szorzat nem valószínű, mert akkor a feltétel egyenértékű azzal, hogy a PAB és PCD háromszőgek (előjeles?) területe egyenlő. Ekkor a P pontnak az AB egyenestől mért távolsága úgy aránylik a CD egyenestől mért távolsághoz, mint a CD és AB szakaszok hossza egymáshoz, a mértani hely egyenes ( ha csak az abszolút értéket vesszük, egyenespár ) , és nem használtuk fel, hogy ABCD érintőnégyszög.
|
| Előzmény: [1080] BohnerGéza, 2008-07-16 02:23:08 |
|
|
| [1079] m2mm | 2008-07-15 19:12:47 |
 Van egy feladat, aminek a megoldására még nem sikerült rájönnöm, de érdekelne. A feladat: Adott egy nem trapéz érintőnégyszög, csúcsai A,B,C,D. Mi azon P pontok mértani helye a síkon, melyekre PA.PB=PC.PD?
|
|
| [1078] BohnerGéza | 2008-07-15 17:42:46 |
 Ismert, hogy ha egy háromszög minden szöge kisebb 120 foknál, akkor az izogonális pont (melyből a háromszög minden oldala 120 fokos szögben látszik) az a pont, melytől a csúcsokig mért szakaszok összege minimális. Látható pl. a [270]. hozzászólásban.
136. feladat: Legyen az ABC háromszög A-nál lévő szöge legalább 120 fok. Bizonyítandó, hogy a PA+PB+PC összeg akkor minimális, ha P=A!
|
|
| [1077] HoA | 2008-06-23 18:07:40 |
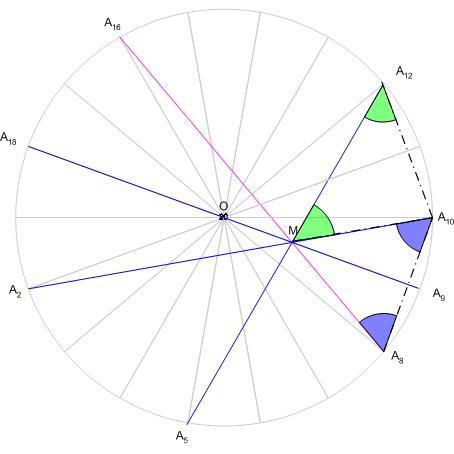
 Segédtétel: A szabályos 18-szög A2A10,A5A12ésA9A18 átlói egy közös M ponton mennek át.
Legyen A2A10ésA9A18 metszéspontja M. Ekkor A2A10 A9A18-ra vonatkozó tükörképe, A8A16 is áthalad M-en. A2A10A8 =A16A8A10 =A16A8A10 =60o , A8A10M =60o , A8A10M szabályos, A10M=A10A8 . De A10A8=A10A12 , mint egyenlő középponti szögekhez tartozó húrok, tehát A10M=A10A12 , MA10A12 szabályos, A10M=A10A8 . De A10A8=A10A12 , mint egyenlő középponti szögekhez tartozó húrok, tehát A10M=A10A12 , MA10A12 egyenlőszárú. MA10A12 egyenlőszárú. MA10A12 =A2A10A12 =A2A10A12 =80o , =80o , 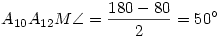 . De A10A12A5 . De A10A12A5 is50o , tehát M rajta van A5A12-n is. is50o , tehát M rajta van A5A12-n is.
|
 |
| Előzmény: [1076] HoA, 2008-06-23 17:35:18 |
|
| [1076] HoA | 2008-06-23 17:35:18 |
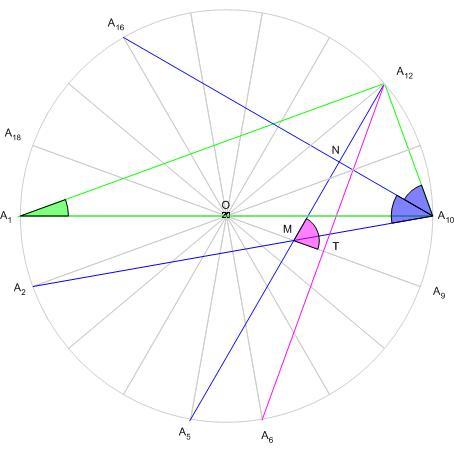
 A KöMaL régebbi olvasói számára ismert, hogy az ilyen feladatok megoldásához, ahol a szögek 10o egész számú többszörösei, jól használható a szabályos 18-szög oldalaiból, átlóiból és körülírt K köréből álló H18 hálózat. Ha ívhossz egységnek K két szomszédos csúcs közötti ívét vesszük, n egységnyi ívhez n.10o kerületi és n.20o középponti szög tartozik. ( Ld. [918] )
Legyenek H18 csúcsai A1,.., A18, K középpontja O, sugara R=1. Húzzuk be az ábrán színessel jelölt átlókat. Az A1A10A12 derékszögű  -ben A10A12=2.sin20o . A12A10A16 -ben A10A12=2.sin20o . A12A10A16 =A2A10A16 =A2A10A16 =40o , A5A12A10 =40o , A5A12A10 =50o . A5A12 metszéspontja A2A10 -zel M, A10A16-tal N. A10NA12 és A10NM egybevágó derékszögű =50o . A5A12 metszéspontja A2A10 -zel M, A10A16-tal N. A10NA12 és A10NM egybevágó derékszögű  -ek, A12N=NM=2.sin20o.sin40o , A12M=4.sin20o.sin40o . Mint azt a segédtételben mrgmutatjuk, M rajta van A9A18-on. A12 tükörképe A9A18-ra A6, A6A12 T-ben merőlegesen metszi A9A18-et. MTA12 derékszögű -ek, A12N=NM=2.sin20o.sin40o , A12M=4.sin20o.sin40o . Mint azt a segédtételben mrgmutatjuk, M rajta van A9A18-on. A12 tükörképe A9A18-ra A6, A6A12 T-ben merőlegesen metszi A9A18-et. MTA12 derékszögű  -ben MA12T -ben MA12T =A5A12A6 =A5A12A6 =10o , A12T=A12M.sin80o=4.sin20o.sin40o.sin80o . A12T egyúttal az OA9A12 egységnyi oldalú szabályos =10o , A12T=A12M.sin80o=4.sin20o.sin40o.sin80o . A12T egyúttal az OA9A12 egységnyi oldalú szabályos  magassága, tehát magassága, tehát 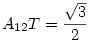 A12T két kifejezéséből a feladat állítása adódik. A12T két kifejezéséből a feladat állítása adódik.
|
 |
| Előzmény: [1067] S.Ákos, 2008-06-17 20:28:38 |
|
|
|
|
| [1072] kromers | 2008-06-18 14:13:43 |
 Szép napot mindenkinek! Egy kis segitségre lenne szükségem. Adott egyenessel adott ponton át párhuzamos egyenes szerkesztése. A szerkesztés menetének több változata is ismeretes. A problémám a következő, hol találom meg ezeknek a BIZONYITÁSÁT? Előre is köszönöm
|
|
| [1071] Euler | 2008-06-18 14:07:27 |
 Nekem is van egy megoldásom, sajnos ehhez is kell trigonometria, de azért érdermes megnézni:(nem tudok képleteket beírni, így egy kicsit hülyén fog kinézni) szorozd be mindkét oldalt 2cos20-al, vedd észre a sin(2x)=2sinxcosx addicios tételt, majd a sin40 négyzetére ismert addicios összefüggést használd( 2sinx.sinx=1-cos(2x). Ezekután ismételten használd a sin160=2sin80cos80 összefüggést, sin160=sin20, kapod, hogy sin80=1/2sin20+(gyök3)/2.cos20, ez pedig nyilván igaz, hiszen a jobb oldalon sin(x+y) áll.
|
| Előzmény: [1067] S.Ákos, 2008-06-17 20:28:38 |
|
|
|
|
| [1067] S.Ákos | 2008-06-17 20:28:38 |
 Valaki tudna mutatni egy elemi geometriai megoldást az alábbi feladatra: Bizbe, hogy 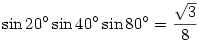 ? ?
|
|
| [1066] bronco | 2008-06-12 01:34:40 |
 Neked is köszönöm szépen, sokat segítettél!
|
|
| [1065] Csimby | 2008-06-11 23:36:54 |
 segítség A pontokat mozgatni lehet. Ha kettőt egymásra teszel, akkor épp 5 érintőt kapsz és abból már látszik hogy kell a szerkesztést csinálni. (veszed az 5 egyenes által meghatározott 5-szöget, kiválasztod az egyik a oldalát, két szomszédos oldal legyen b és c. A b és c re eső 4 csúcsot "keresztbe" összekötöd, a metszéspon legyen M. Ekkor M-en és az a-val szemben lévő csúcson átmenő egyenes kimetszi a-ból az a-ra eső érintési pontot)
|
| Előzmény: [1064] bronco, 2008-06-11 23:21:28 |
|
| [1064] bronco | 2008-06-11 23:21:28 |
 Sziasztok!
Egy projektív geometriai feladatban lenne szükségem segítségre:
Adott egy kúpszelet öt érintőegyenese. Szerkeszzük meg az egyiken az érintési pontot!
Egyszerűnek tűnik, de sehol sem találok hasonló megoldott feladatot. (Annyi tudok, hogy a Brianchon-tétel elfajuló esetét kell alkalmazni.)
Előre is köszi!
|
|
|
| [1062] SmallPotato | 2008-06-05 11:53:17 |
 A feladat értelmében a paralelogramma egyik átlója adott (a kör sugara), továbbá szögei is adottak.
Rajzoljuk fel az ismert átlóra az ismert szög látókörét. Az átló végpontjai és a látókör-ív egy futó pontja olyan háromszöget határoznak meg, amelynek területe a paralelogramma területének fele. E háromszög területe viszont akkor maximális, ha a rögzített oldalhoz tartozó magassága maximális, azaz a látókör-ív felében álló harmadik csúcs esetén. Eszerint a paralelogramma területe ott maximális, ahol a paralelogramma oldalai egyenlők, azaz ha a paralelogramma rombusz, vagyis ha a hiányzó negyedik csúcs a körcikk ívének felezőjében van.
|
| Előzmény: [1061] Euler, 2008-06-05 11:30:15 |
|
| [1061] Euler | 2008-06-05 11:30:15 |
 Hello mindenkinek! Van egy geometria feladatom, melyre teljesen elemi geometriai megoldást szeretnék hallani, már kijött trigonometriával, de léteznie kell elemi geos megoldásnak is. Ha valakinek van ötlete, legyen szives ossza meg velem is! Előre is köszi, a feladat: Adott egy körcikk, melynek középponti szöge hegyesszög. A körcikkbe olyan paralalogrammákat irunk, amelynek oldalai párhuzamosak a szögszárral, egyik csúcsa a szögcsúcs, 2 a szárakon van és a negyedik a köríven. Mikor maximális a területe a paralelogrammának?
|
|
| [1060] BohnerGéza | 2008-06-05 10:52:40 |
 Nem! Kellett és szép volt a megoldásod! Ez utóbbi megoldás, csak a 134/a feltételei mellett megy.
Egymást metsző köröket nem lehet koncentrikussá képezni, illetve, ha a két egymást nem metszö körhöz tartozó mindkét nullkörön átmegy a harmadik, akkor annak képe egyenes lesz.
|
| Előzmény: [1059] HoA, 2008-06-05 00:02:58 |
|
| [1059] HoA | 2008-06-05 00:02:58 |
 Hát igen. És ezek szerint jól sejtettem, hogy a 134. feladat megoldása is ez: legyen I az az inverzió, amely k1 -et és k2 -t koncentrikus körökbe képezi le, ekkor akárhová is esik k3' középpontja, a három körközéppont valójában kettő, és így egy egyenesen vannk.
|
| Előzmény: [1058] BohnerGéza, 2008-06-04 20:29:36 |
|
|
| [1057] HoA | 2008-06-04 15:52:46 |
 Csak nem az a galád trükk lett volna a 134. feladat eredeti megoldása, hogy ha három pontból kettő egybeesik, akkor egy egyenesen vannak? Az eredeti kitűzésbe ez is belefér. A 135. feladat ábrája ismerős a "Fejezetek az elemi geometriából" c. könyvből. Ez az ottani feladat általánosítása. Eredetileg azt kellett igazolni, hogy ha "1" valamilyen helyétől indulva a körsorozat n körből áll és "n" érinti "1" -et, akkor ez "1" tetszőleges helyéről indulva is fennáll. A kapcsolatot 134. -gyel ott vélem felfedezni, hogy 135. megoldásának kulcsa is két egybeeső körközéppont.
|
| Előzmény: [1056] BohnerGéza, 2008-06-04 12:50:33 |
|
|
| [1055] HoA | 2008-06-04 10:00:34 |
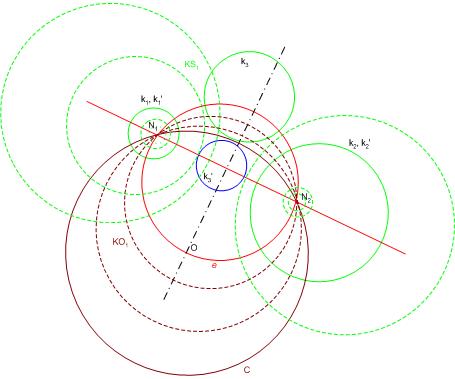
 A 134/a feladat megoldása: Az egymást nem metsző k1 és k2 körök által maghatározott körsor legyen KS1 , nullkörei N1 és N2 . k3 ne haladjon át N2-n, a k3 és N2 által maghatározott körsor legyen KS2 , ennek másik nullköre N3 , a keresett inverzió I, alapköre C, ennek középpontja O. Mivel egy elliptikus körsor köreinek középpontjai a nullkörök által meghatározott egyenesen vannak, köreink inverzeinek, k1',k2'ésk3' köröknek a középpontjai csakkor lesznek egy egyenesen, ha N1' N2' és N3' is. N1' és N2' e1' egyenese I-nél a KS1 körsor ortogonális korsora, KO1 azon ko1i körének lesz az inverze, amelyik O-n áthalad, vagyis az N1 , N2 és O pontok által meghatározott körnek. Hasonlóan N2' és N3' e2' egyenese a KS2 körsor ortogonális korsora, KO2 azon ko2j körének lesz az inverze, amelyik O-n áthalad, vagyis az N2 , N3 és O pontok által meghatározott körnek. e1' és e2' tehát csakkor azonos, ha ko1i és ko2j azonosak, vagyis ko1i = ko2j az N1 , N2 és N3 pontok által meghatározott kör, melyre O is illeszkedik. Ez persze az ortogonalitás miatt megegyezik [1049] e körével, így a megoldás folytatható az ott leírtak szerint, a nullkörök és körsorok megszerkesztése nem szükséges. Az egyszerűbb gyakorlati kivitelezést eredményező O és C megválasztás ebben a terminológiában úgy fogalmazható, hogy legyen C a KO1 azon köre, melynek O középpontja e -re illeszkedik. Ekkor KS1 inverze önmaga.
|
 |
| Előzmény: [1053] BohnerGéza, 2008-05-30 23:09:00 |
|
| [1054] HoA | 2008-06-02 13:42:59 |
 További segítségként a 134/a feladathoz feloldom az [1048]-beli észrevételt: Két kör által meghatározott körsor nullköreinek inverze adott inverziónál megegyezik a körsor inverzének nullköreivel.
|
| Előzmény: [1053] BohnerGéza, 2008-05-30 23:09:00 |
|
| [1053] BohnerGéza | 2008-05-30 23:09:00 |
 Pontosítom a feltételt, ezzel segítek is: 134/a feladat: A 134. feladatban tegyük meg ezt a kikötést: a 3 kör közt van kettő, melyek nem metszik egymást, és az általuk meghatározott körsor legalább egyik nullkörén nem megy át a harmadik kör. Ekkor HoA előbbi megoldásán túl adódik egy másik megoldás is.
|
| Előzmény: [1052] BohnerGéza, 2008-05-28 20:19:50 |
|
|
| [1051] BohnerGéza | 2008-05-28 20:13:06 |
 Köszönöm HoA megoldását, egyben kitűzöm könnyítve a feladatot:
134/a feladat: A 134. feladatban tegyük meg azt a kikötést, hogy a 3 körnek nem lehet közös pontja. Így az előbbi mo-tól eltérő is megadható!
|
| Előzmény: [1050] HoA, 2008-05-28 08:11:09 |
|
|
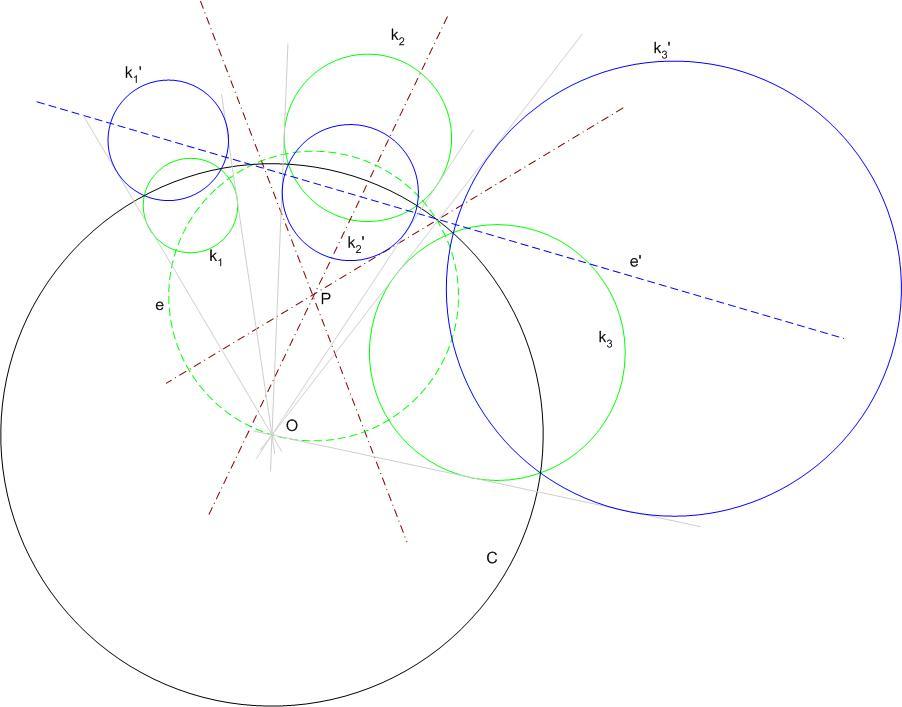
| [1049] HoA | 2008-05-28 08:10:03 |
 Legyenek az adott körök k1,k2ésk3, a keresett inverzió I, alapköre C, ennek középpontja O. A körök inverzei k1',k2'ésk3' , e három kör közös szimmetriatengelye e' . Mivel az inverzió saját inverz művelete, k1',k2'ésk3' inverze I-nél k1,k2ésk3. O nem lehet e'-n, mert ekkor a szimmetria miatt k1,k2ésk3 is közös szimmetriatengellyel rendelkezne és nem lehet valamelyik ki'-n sem, mert akkor ki egyenes lenne. Legyen e' inverze e. e-ről megállapítható, hogy
-kör, mert O nincs e'-n
-átmegy O-n, mert e' egyenes
-merőlegesen metszi a k1,k2ésk3 köröket az inverzió szögtartó tulajdonsága miatt.
Adottnak véve k1,k2ésk3 köröket, a keresett inverzióra szükséges feltétel, hogy O középpontja egy olyan e körön legyen, amelyik merőlegesen metszi a k1,k2ésk3 köröket , de ne legyen a körök egyikén sem, hiszen akkor ki' egyenes lenne. Megmutatjuk, hogy a feltétel elégséges is. Legyen e a k1,k2ésk3 köröket merőlegesen metsző kör, O ennek egy - a körökkel nem közös - pontja. Az O középpontú inverziónál a k1,k2ésk3 körök képe három kör lesz, k1',k2'ésk3'. e képe az e' egyenes, amely a szögtartó tulajdonság miatt merőlegesen metszi k1',k2'ésk3' köröket. Mivel egy kört metsző egyenesek közül csak az átmérő egyenesek metszenek merőlegesen, e' mindhárom körnek átmérő egyenese, tehát a három körközéppont egy egyenesen van.
e szerkesztéséhez felhasználjuk, hogy merőlegesen metsző körök esetén az egyik kör metszéspontba mutató sugara a másik kör érintője. e középpontjából, P-ből tehát a k1,k2ésk3 körökhöz egyenlő érintők húzhatók, P a három kör hatványpontja. A szerkesztés menete:
- megszerkesztjük k1,k2ésk3 P hatványpontját mint a körpárok hatványvonalainak metszéspontját - megszerkesztjük a P középpontú, k1-et merőlegesen metsző e kört - e tetszőleges, a körökre nem illeszkedő pontját a kersett inverzió O középpontjául választva tetszőleges sugarú C alapkörrel végrehajtjuk az inverziót. (1. ábra)
Egyszerűbb a gyakorlati kivitelezés, ha O-t úgy választjuk, hogy két kör, például k1ésk3 hatványvonalára illeszkedjék. Ekkor C úgy választható, hogy k1-et és k3-at merőlegesen messe, így ezek az inverzió során önmagukra képeződnek (2. ábra a következő hozzászólásban)
|
 |
| Előzmény: [1042] BohnerGéza, 2008-05-18 23:09:18 |
|
| [1048] HoA | 2008-05-21 15:53:40 |
 Segítség a 134. feladathoz:
- Ha három pont nincs egy egyenesen, akkor egy körön vannak
- Melyik három pont? ( A körközéppont inverz képe általában nem az inverz kör középpontja.)
|
| Előzmény: [1042] BohnerGéza, 2008-05-18 23:09:18 |
|
| [1047] Kata12 | 2008-05-21 11:43:02 |
 Kedves Géza!
Nagyon szépen köszönk minden segítséget! Hasznos volt.
|
|
|
| [1045] Kata12 | 2008-05-20 18:45:52 |
 Szia Géza!
Nagyon köszönöm a segítséget, esetleg az háromszöges példát tudnád kicsit részletesebben leveztni ha lehet ábrával?
|
|
|
| [1043] Kata12 | 2008-05-20 16:00:04 |
 Sziasztok!
Két szerkesztési feladat megoldásában kérném a segítségeteket, amelyet az euklides szerkesztő programban kellene megszerkesztenem
1, Szerkesszünk egyenlő szárú háromszöget, ha adott az alap és a szár különbsége, továbbá a szárak közti szög.
2, Szerkesszünk négyszöget, ha ismert két átlója, az átlók szöge és a két szomszéédos szöge.
Előre is köszönöm a segítséget: Kata
|
|
| [1042] BohnerGéza | 2008-05-18 23:09:18 |
 134. egy nehéz feladat:
Adott 3 kör, melyek középpontjai nincsenek egy egyenesen. Adjunk meg olyan inverziót, melynél a körök képe kör marad, de ezek kp-jai már egy egyenesen vannak.
|
|
|
