| [130] lorantfy | 2004-04-27 18:31:12 |
 Kedves Géza!
Jó ez a szögfelezős megoldás és egyszerűbb is mint az enyém.
Azt szeretném kérdezni, hogy az indexelt pont megjelölést az Euklidesben hogy csinálod? (pl A1). Lehet, hogy csak az újabb verzió engedi meg? (Enyém 2.02.)
|
 |
| Előzmény: [129] BohnerGéza, 2004-04-27 14:46:47 |
|
| [129] BohnerGéza | 2004-04-27 14:46:47 |
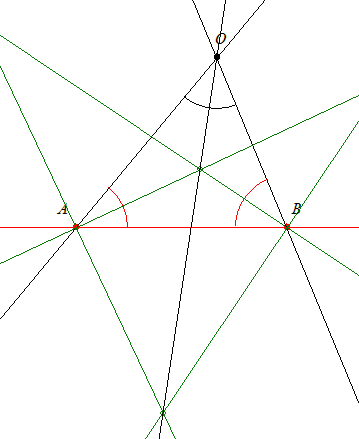
 29. feladat: ( A [123] hozzászólás 28. feladata. )Igazoljuk, hogy tompaszögű háromszögben a talpponti és eredeti háromszög területének aránya kettőnél kisebb, nem negatív érték!
[125] 28. feladatának megoldása: Legyen a két nem párhuzamos egyenes metszéspontja O, a két egyenes további egy-egy pontja A ill. B. Az OAB háromszög A-nál és B-nél lévő külső szögfelezőivel szerkeszthető az O-nál lévő belső egy pontja. Hasonlóan kapjuk egy másik pontját is.
|
| Előzmény: [125] Hajba Károly, 2004-04-27 12:18:39 |
|
| [128] lorantfy | 2004-04-27 14:19:02 |
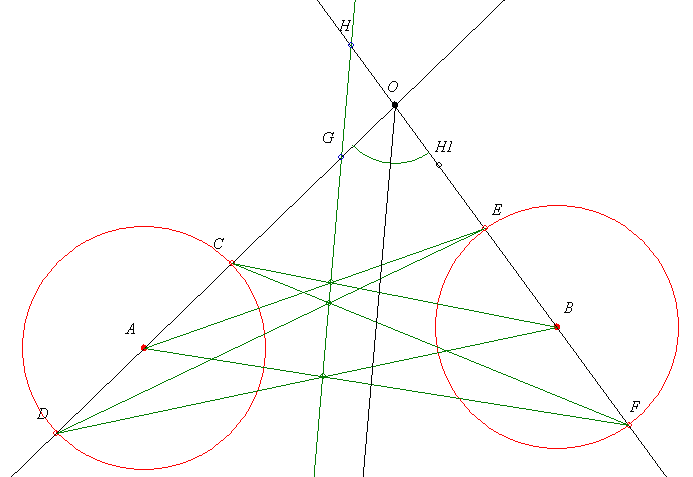
 28. megoldás vázlat: Használjuk a Papposz tételt. Vegyünk fel a szögszárakon tetszőleges A és B pontot. Ezekből ugyanazzal a sugárral körözve kapjuk a szögszárakon a C,D és E,F pontokat. Szóval felveszünk a szögszárakon 3-3 pontot azonos távolságokkal. A megfelelő metszéspontokat összekötve ezek egy egyenesen lesznek, mondja Papposz. Mivel a szakaszok egyenlőek ez az egyenes párhuzamos a szögfelezővel, gondolom én. (A bizonyítást másra hagyom!). A szögszárakból kimetszett G,H pontokból a szögfelező megszerkeszthető a egyenesek metszéspontjának felhasználása nélkül.
|
 |
| Előzmény: [125] Hajba Károly, 2004-04-27 12:18:39 |
|
|
|
| [125] Hajba Károly | 2004-04-27 12:18:39 |
 28. feladat:
Szerkesszük meg két nem párhuzamos egyenes szögfelező(jé/i)t a metszéspont felhasználása nélkül!
HK
|
|
|
| [123] BohnerGéza | 2004-04-25 23:43:53 |
 A versenyfeladatok [15]-ben szereplő és a következő hozzászólásokban megoldott ott 6. feladattal kapcsolatban tűzöm ki az alábbit.
Ráadásul egy kis adalék az Euklideshez. Megnéztem vele, hogy mennyi lehet a talpponti és eredeti háromszög területének aránya.
A szorzásokat és az arányszámolást a párhuzamos szelők tételével szerkesztettem meg. Hegyesszögű háromszög esetén kijött a már megoldott 0<=arány<=1/4. A valószínű eredmény tompaszögűre 0<=arány<2.
28. feladat: Igazoljuk, hogy tompaszögű háromszögben a talpponti és eredeti háromszög területének aránya kettőnél kisebb, nem negatív érték!
|
|
| [122] lorantfy | 2004-04-25 19:13:17 |
 Kedves Géza és Fórumosok!
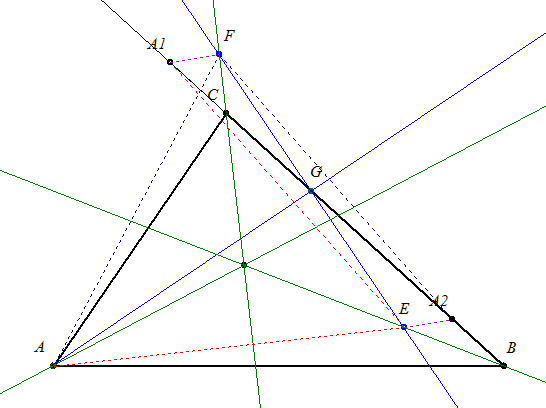
Nagyon szép a megoldás. Én is próbálkoztam tükrözéssel, de nem jött össze. Minthogy már kész az ábrám 22. megoldása alapján rögtön megvan a 20. feladat megoldása: Tükrözzük az A pontot a B-n és C-n átmenő belső szögfelezőkre. Így BA1=c és CA2=b.
G a beírt kör érintési pontja, tehát CG=s-c és BG=s-b. Ezekből A1G=c-(s-b)=c+b-s és A2G=b-(s-c)=b+c-s vagyis A1G=A2G. Létezik az A1EA2F paralelogramma, ahol E és F a szögfelezőkön lévő pontok és G felezi EF szakaszt. Ekkor a paralelogramma szemközti oldallai: A1E=FA2. A tükrözések miatt:
A1E=AE A2F=AF AE=AF AE=AF
AEF egyenlő szárú háromszögben EF merőleges AG-re.
|
 |
| Előzmény: [121] BohnerGéza, 2004-04-25 16:38:35 |
|
| [121] BohnerGéza | 2004-04-25 16:38:35 |
 Köszönöm DS megoldását a 22. feladatra, lehet belőle tanulni.
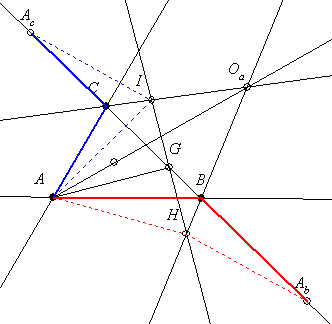
22. feladat megoldása: Ha szögfelező ( felezőpont, oldalfelező merőleges ) szerepel tükrözzünk rá! Így kaptuk az Ab és Ac pontot. Mivel CG=s-b, így AcG=s, hasonlóan AbG=s. Tehát G felezőpontja AcAb-nek, ezért csakkor felezőpontja IH-nak, ha HAbIAc paralelogramma. Ilyen paralelogramma pontosan egy létezik, amelynek H pontját a COa G-re vonatkozó tükörképe metsz ki BOa-ból. Ekkor AcI=IA és AbH=HA miatt AI=AH, tehát AG merőleges IH-ra és viszont.
Azt hiszem még ezek után is érdemes az analóg 20. feladat megoldását végiggondolni.
|
 |
| Előzmény: [118] DS, 2004-04-23 14:53:57 |
|
| [120] Hajba Károly | 2004-04-25 09:45:29 |
 Egy kis hazai :o)
27. feladat:
a) Keressünk olyan síklapokkal határolt térbeli idomo(ka)t, mely(ek)nek minden pontját minden ponttal él köt össze.
b) Keressünk olyan síklapokkal határolt térbeli idomo(ka)t, mely(ek)nek minden lapja minden lappal határos.
c) Vajon indokolt-e a többesszám?
HK
|
|
| [119] lorantfy | 2004-04-24 01:30:00 |
 Kedves DS!
A megoldásod olvasásakor a bennem működő "hányan értik ezt a középiskolás olvasók közül" műszer mutatója a piros sávba lendült így ne haragudj, de pár megjegyzést is teszek az ábra mellé: X ideális pont az IH egyenesen végtelen távol lévő pontot jelöl.
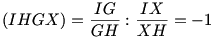
Ez gyakorlatilag azt jelenti: IG=GH.
A szakaszok aránya helyett lehet az O pontból induló őket kimetsző egyenesek által bezárt szögek szinuszainak arányát vizsgálni. (Az X pontot az IH-val párhuzamos OX egyenes "metszi ki".) Ezt jelenti (OI,OH,OG,OX)=-1.
Az AD- ha jól értem - itt az AG egyenest jelenti.
|
 |
| Előzmény: [118] DS, 2004-04-23 14:53:57 |
|
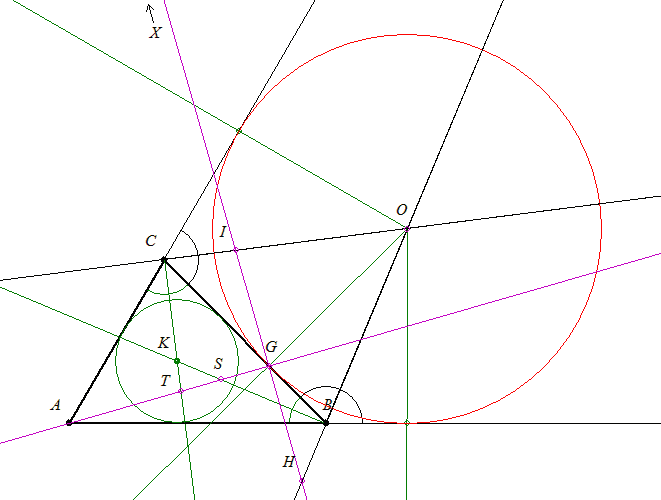
| [118] DS | 2004-04-23 14:53:57 |
 Géza bátorított, hogy írjam le a megoldásomat a 22-es feladatra. (A 20-as is megy ennek mintájára.) Legyen az IH egyenes ideális pontja X, a BC oldalhoz írt kör középpontja O. Elég azt megmutatnunk, hogy (IHGX)=-1. Áttérve egyenesekre (OI, OH, OG, OX)=-1 kéne. Nekem kényelmesebbnek tűnt a rájuk merőleges egyenesekkel dolgozni: ezek C és B szögfelezői, a BC oldal és az AG egyenes. Ezek ugyan nem mennek át egy ponton de az egymással bezárt szögek sinusainak arányát így is felírhatjuk. Ez az első három egyenesnél sin tétellel KB:KC, a másik szükséges arány pedig KT:KS. (K a beírt kör középpontja, AD a C és B szögfelezőit T-ben és S-ben metszi.) Az maradt, hogy KB:KC=-KS:KT, ami pedig igaz, hiszen KB:KS=(c-b):a, illetve KC:KT=(b-c):a. Az utóbbi arányokat kiszámolhatjuk pl súlyozgatással, ugyanis a szögfelezők és AD is egyaránt jól ismert arányban metszik a szemközti oldalakat. Remélem Géza megörvendeztet bennünket egy elegánsabb gondolatmenettel.
|
|
| [117] BohnerGéza | 2004-04-23 11:11:32 |
 Elég hosszú minden húrnégyszög?
A következő feladat ötlete Csimby ujjgyakorlatok [135]-ben megjelent 42. feladatából adódott. Megoldásával még nem foglalkoztam.
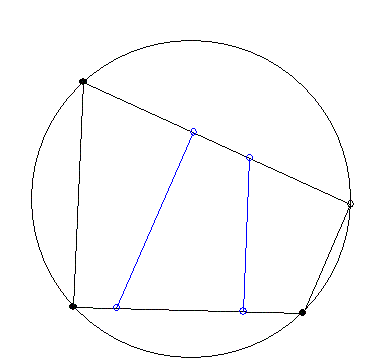
26. feladat: Nevezzük elég hosszúnak a húrnégyszöget, ha szemközti oldalaival párhuzamosan húzott egy-egy vonallal három húrnégyszögre bontható. A kérdés: Elég hosszú minden húrnégyszög? Azaz valamelyik irányban fölbontható?
Az ábrán lévő igen.
|
 |
|
|
| [115] BohnerGéza | 2004-04-20 20:44:31 |
 A 23. és 24. feladathoz hasonló, kicsit nehezebb feladat:
25. feladat: Szerkesztendő háromszög, ha adott egy oldala, a vele szemközti szög és az ehhez tartozó szögfelező. (a szögfelezőnek a háromszögbe eső darabja)
A 20. és 22. feladat egyikének megoldását, ha addig másvalaki nem teszi, kb. a hónap végén közlöm.
|
|
|
| [113] BohnerGéza | 2004-04-16 14:13:22 |
 Kedves László!
Köszönöm a rajzokra vonatkozó tanácsokat!
Kicsit reméltem, hogy a [107]-es hozzászóllásom tovább érvényben marad, hogy az Euklides-szel többen foglalkozzanak. Adok viszont egy nehezebb feladatot:
24. feladat: ABC háromszög beírt körének kp-ja O. Szerkesztendő a háromszög, ha adott c, gamma és OC.
|
| Előzmény: [111] lorantfy, 2004-04-14 00:44:49 |
|
| [112] Csimby | 2004-04-14 01:19:36 |
 Van két új geometria példa az újgyakorlatoknál amit eredetileg ide szántak ;-)
|
|
| [111] lorantfy | 2004-04-14 00:44:49 |
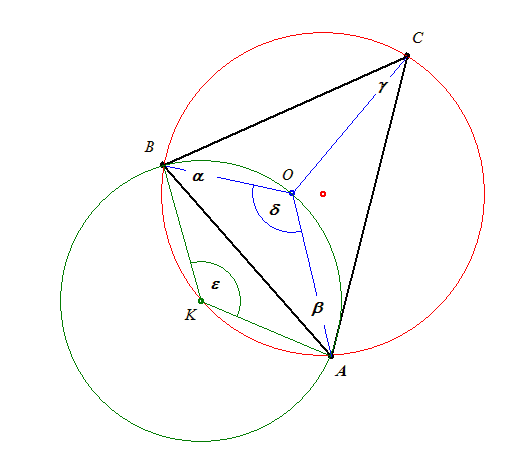
 Kedves Géza!
Igaz a sejtésed, ugyanis:
Az O pont az AB fölé emelt 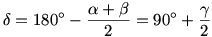 látóköríven van. látóköríven van.
Ennek a látókörívnek a K középpontjából AB szakasz 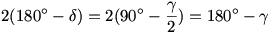 szögben látszik. Tehát a látókörív középpontja valóban a szögben látszik. Tehát a látókörív középpontja valóban a  köré írt körön van. köré írt körön van.
A szerkesztés akkor történhet úgy, hogy felvesszük a körülírt kört és abba az AB oldalt, mint húrt. Ennek felező merőlegese kimetszi a körből a K1, K2 pontokat. Ezekből, mint középpontokból megrajzolhatjuk az AB fölé emelt látókörívek körbe eső íveit. Ezekből az AB-től r távolságban futó párhuzamosok kimetszik a a beírt kör középpontját.
BAO  -t megduplázva, a szögszár kimetszi C-t a körből. -t megduplázva, a szögszár kimetszi C-t a körből.
|
 |
| Előzmény: [108] BohnerGéza, 2004-04-13 21:49:21 |
|
| [110] Pach Péter Pál | 2004-04-14 00:34:02 |
 23. feladat megoldásának vázlata
Adottak r,R,a. Az ismert d2=R2-2Rr-ből megvan d is, ami a két kör középpontjának távolsága, d szerkeszthető is. :-) Rajzolunk két kört R, illetve r sugárral úgy, hogy középpontjaik távolsága d. R és a segítségével megkapjuk  -t (ez az eddigiektől független lépés), azoknak a pontoknak a helye, amelyekből a beírt kör -t (ez az eddigiektől független lépés), azoknak a pontoknak a helye, amelyekből a beírt kör  szög alatt látszik, egy olyan kör, amely a beírt körrel koncentrikus, és a sugara egyszerűen megkapható. (Megszerkesztjük egy pontját, ez is megy körzővel…) A kapott körnek és a köréírt körnek a metszéspontja A, érintőket húzunk a beírt körhöz, ezek A-tól különböző metszéspontja a köré írt körrel B és C, valamilyen sorrendben. Ha van ilyen ABC háromszög, akkor azt megkaptuk. szög alatt látszik, egy olyan kör, amely a beírt körrel koncentrikus, és a sugara egyszerűen megkapható. (Megszerkesztjük egy pontját, ez is megy körzővel…) A kapott körnek és a köréírt körnek a metszéspontja A, érintőket húzunk a beírt körhöz, ezek A-tól különböző metszéspontja a köré írt körrel B és C, valamilyen sorrendben. Ha van ilyen ABC háromszög, akkor azt megkaptuk.
Diszkusszió…
|
| Előzmény: [106] Gubbubu, 2004-04-13 10:13:43 |
|
| [109] lorantfy | 2004-04-13 23:29:47 |
 Kedves Géza és Fórumosok!
Én az Euklides programból a következőképpen nyerem ki a színes ábrát:
1.Az Euklidesben megszerkesztett képet beállítom szépen középre, fehér háttérrel és a Print Screen gombbal a vágólapra másolom.
2.A Pain rajzoló programban Beillesztés, majd kijelölöm az ábra megfelelő részét és átmásolom egy új lapra.
3.Az ábra külső méretét a lehető legkisebbre veszem. Itt még a feliratokat és a betűzést is lehet pontosítani, pl. görög betűt a szögeknek stb. Majd elmentem „gif” formátumban.
4.Ezt az ábrát már fel lehet tölteni a Fórumba.
Annyit szoktam még csinálni az ábrával, hogy még bitmap (bmp) formában megnyitom az MS. Photo Editorral és átlátszó hátteret adok neki, majd ezután mentem „gif” formátumban. Igy az ábrát feltöltve az alapszinen (sárga) jelenik meg.
Aki tud egyszerűbbet írja be!
|
| Előzmény: [108] BohnerGéza, 2004-04-13 21:49:21 |
|
|
| [107] BohnerGéza | 2004-04-13 21:27:32 |
 A 23. feladathoz: Csak pár percem volt, csak az Euklides-szel (szerkesztőprogram, letölthető az euklides.hu-ról) néztem meg. Megadtam az A és B pontot, a körülírt kört. majd „nyomvonal” segítségével kirajzoltattam az ABC beírt körének kp-jának helyeit, ha a C végigfut a körön. Úgy tűnik, hogy a körülírt körben lévö két olyan ívet kaptam, melyek a körülírt körön lévő kp-ú körök ívei. A rajz remélem segít, bár sajnos a terjedelmi korlát miatt nem túl jó. Sőt most valamiért nem is sikerül a feltöltése. (Szívessen venném, ha valaki segítene, hogy lehet jobb ábrát felrakni!)
Ha igaz a fenti sejtés, akkor az alapján a szerkesztés megy. Bizonyítással próbálkozom majd.
|
|
| [106] Gubbubu | 2004-04-13 10:13:43 |
 23.feladat: Szerkesszünk háromszöget, ha adott egy oldala, illetve a beírt és a körülírt kör sugara.
Megjegyzés: még csak 5-6 percet tudtam gondolkodni e feladaton, lehet hogy az átlagnál nehezebb, az is hogy nagyon könnyű.
|
|
| [105] BohnerGéza | 2004-04-05 10:00:57 |
 Kedves Csimby!
Észrevételed, segítséged helyes, de kiegészítésként: Az összes Apollonios-feladat megoldható inverzió nélkül is. (101. hozzászolás) Talán ezzel is segítettem valakinek.
A 21. feladat átfogalmazásához: Hiperbola ill. ellipszis: Azon kőrők középpontjainak mértani helye (halmaza), melyek átmennek az egyik fókuszon és érintik a másik fokusz közáppontú 2a (nagytengely) sugarú kört.
|
|
| [104] Csimby | 2004-04-04 23:12:03 |
 A 21. feladat-hoz csak annyit mondanék segítségnek, hogy inverzió!
|
|
|
| [102] BohnerGéza | 2004-03-29 15:55:10 |
 A 22. feladat: Legyen az ABC háromszög BC oldalához írt körének BC-n lévő érintési pontja G. Igazold, hogy az AG-re G-ben állított merőlegesnek a B ill. C csúcsnál lévő külső szögfelező közti szakaszát G felezi!
|
|
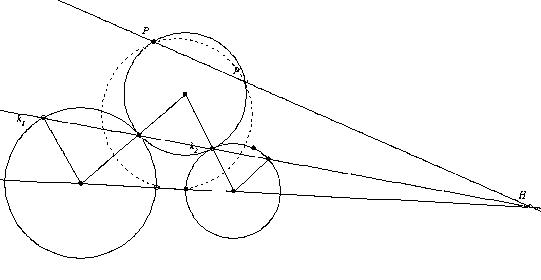
| [101] BohnerGéza | 2004-03-29 15:49:36 |
 Egy ábra [99] Csimby 21. feladatához.
A feladat nehéz, ez csak segítség.
A k1 és k2 kört érintő P-n átmenő kört érintő kör a szerkesztendő. A H hasonlósági pont? A P' szerkesztésével egy másik feladatra vezettük az eredeti átfogalmazását!
|
 |
|
| [100] BohnerGéza | 2004-03-23 14:59:39 |
 22. feladat: A 20. feladat alapján fogalmazzuk meg az analóg új feladatot. (beírt kör érintési pontja helyett ...) Megoldása természetesen hasonlóan megy, mint a 20-é.
Gondolkodom, van-e értelme egy olyan új fórumtémának, melynek neve "Új" feladatok . Ebben, a fórumban megjelent feladatok alapján, analóg feladatokat, átfogalmazásokat, vagy a megoldásuk során felmerült, ott kitalált új feladatokat írhatnánk meg. A tanításban és tanuláskor is jól jöhetnek az ilyen ötletek.
Például a 21. feladat átfogalmazása: Adott két kör és egy pont. Szerkesszük meg a két kört érintö, a ponton áthaladó kört.
|
|
| [99] Csimby | 2004-03-22 22:32:07 |
 21.feladat Szerkesszük meg körzővel és vonalzóval két hiperbola metszéspontjait, ha a két-két fókuszpont közül kettő egy pontba esik.(Tehát adott a 3 fókuszpont és a két főtengely hossza)
|
|
|
| [97] BohnerGéza | 2004-03-19 11:20:27 |
 20. feladat: Legyen az ABC háromszög beírt körének BC-n lévő érintési pontja D. Igazold, hogy az AD-re D-ben állított merőlegesnek a B ill. C csúcsnál lévő belső szögfelező közti szakaszát D felezi!
|
|
|
| [95] Pach Péter Pál | 2004-03-09 18:16:18 |
 A 19. feladat mindhárom része megoldható vektorok használatával is: (R most is a kör sugara)
Legyen  , ahol X=A,B,C,D,P Vegyük észre, hogy 2p=a+b+c+d. (Pl. a+b abba a pontba mutat, amelyet úgy kapjuk, hogy O-t tükrözzük AB-re. Így a jobboldalon álló vektor abba a pontba mutat, amelyet úgy kapjuk, hogy O-t tükrözzük P-re.) , ahol X=A,B,C,D,P Vegyük észre, hogy 2p=a+b+c+d. (Pl. a+b abba a pontba mutat, amelyet úgy kapjuk, hogy O-t tükrözzük AB-re. Így a jobboldalon álló vektor abba a pontba mutat, amelyet úgy kapjuk, hogy O-t tükrözzük P-re.)
AB merőlges CD-re, ezért (a-b)(c-d)=0. Könnyen látszik, hogy (a+b)(c+d)=0. Így 4p2=(a+b+c+d)2=4R2+2(ab+cd). Ezért ab+cd állandó. Így 2AB2+2CD2=2((a-b)2+(c-d)2=(a-b+c-d)2+(a-b+c-d)2=8R2-4(ab+cd), ami állandó.
4(AP2+BP2+CP2+DP2)=4((p-a)2+(p-b)2+(p-c)2+(p-d)2=(-a+b+c+d)2+(a-b+c+d)2+(a+b-c+d)2+(a+b+c-d)2=4(a2+b2+c2+d2)=16R2, ami állandó.
AC2+CB2+BD2+DA2=(a-c)2+(c-b)2+(b-d)2+(d-a)2=8R2-2(a+b)(c+d)=8R2.
|
|
| [94] Zormac | 2004-03-09 14:32:34 |
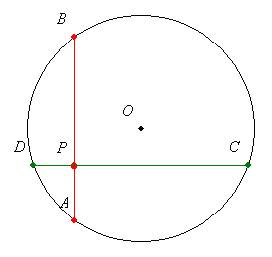
 A húrdarabok szorzata esetében a pont körre vonatkozó hatványát érdemes segítségül hívni, de szerintem az a) rész kijön a másik kettő nélkül is:
Legyen a kör sugara R, az OP távolság r, az AB és CD húrok távolsága O-tól rendre x és y. Pitagorasz szerint:
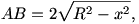 | (1) |
illetve
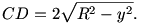 | (2) |
(1) és (2) összegéből
AB2+CD2=4(2R2-r2)
adódik, ami független a húrok irányától.
|
| Előzmény: [93] lorantfy, 2004-03-08 11:22:19 |
|
| [93] lorantfy | 2004-03-08 11:22:19 |
 Kedves Zoltán!
Kösz a megoldást! Innen már nincs messze az a.) rész megoldása sem. Ha már megvan a húrdarabok négyzete akkor már csak a húrdarabok kétszeres szorzata kell az összeg négyzetéhez!
|
 |
| Előzmény: [92] SchZol, 2004-03-08 09:28:29 |
|
|
| [91] lorantfy | 2004-03-06 09:56:09 |
 19. feladat:
Adott az r sugarú kör belsejében egy P pont. AB és CD húrok a P pontban merőlegesen metszik egymást.
a.) Bbh. AB2+CD2 független a húrok helyzetétől!
b.) Bbh. AP2+BP2+CP2+DP2 független a P pont helyzetétől!
c.) Bbh. ACBD húrnégyszögben AC2+CB2+BD2+DA2=8r2
(Az a.) és b.) pont Strohmajer János: Geomatria példatárából, a c.) pedig Olah György: Határon túli matematika versenyek c. könyvéből való. Lásd. könyvajánlatban!)
|
 |
|
|
|
|
| [87] BohnerGéza | 2004-03-03 13:36:16 |
 A 17. feladat [75] megoldása:
Több lehetőség közül kettő mutatok. Lehetne az ívek középpontja az átlóegyenes más pontja is. Egyszerűnek, de érdekesnek gondolom a második megoldás csúszkája keresztmetszetének megszerkesztését.
Természetesen csak vázlatok az alábbiak.
|
 |
|
| [86] Kristóf Miklós | 2004-03-02 12:08:35 |
 Kedves Géza és Mindenki! Az ötszöges feladat első kérdése túl könnyű, a második túl nehéz. Szerintem legyen ez a feladat: készítsünk szabálytalan ötszögekből poliédert úgy hogy csak 3 és 4 élű csúcsok legyenek. Legyen n a 4 élű csúcsok száma, adjuk meg a poliéder lapjainak, csúcsainak és éleinek számát n függvényében. Próbáljunk meg minél több n-re megkonstruálni ilyen poliédert! Mely n-re nem létezik megoldás? Melyikre van több különböző? Reprezentatív példa: n=3-ra létezik megoldás, 18 lap, 29 csúcs és 45 él van ezen a jószágon. Oktadekaéder?
|
 |
| Előzmény: [85] Kós Géza, 2004-03-01 15:41:20 |
|
| [85] Kós Géza | 2004-03-01 15:41:20 |
 Kedves Mindenki,
Az ötszöges feladatot ki fogjuk tűzni a pontversenyben. Ezért azt szeretném kérni, hogy a feladatról egyelőre senki ne írjon semmit, és eredményeit ne árulja el senkinek. (Utána majd alaposan megtárgyaljuk a megoldást.) Köszönöm.
Kós Géza
|
| Előzmény: [67] Kristóf Miklós, 2004-02-24 10:56:07 |
|
| [84] Kristóf Miklós | 2004-03-01 13:44:57 |
 Kedves Sirpi! A válaszod tökéletes és korrekt, egyben irigyellek azért mert te a matek képleteket így be tudod írni, nekem fogalmam sincs hogy kell. De ezzel hogy ezt megválaszoltad, következhet az igazi kérdésem, ami egy számomra már-már misztikus jelenségre utal: de most látom csak hogy a válaszod megoldást ad erre is! Mindegy, azért leírom: Ha egy n oldalú sokszög szögei helyett mindenütt alfa szöget írok, ahol alfa az n oldalú szabályos sokszög szöge, akkor a képlet helyes marad. Ennek oka az hogy az n oldalú sokszög szögeinek összege mindig ugyanannyi, (n-2)180 fok! Ennek ennedrésze a sokszög szöge. Így minden csúcshoz rendelhetünk egy ún. formális szöghiányt, amit úgy kapok meg, hogy minden sokszöget szabályosnak tekintek, és eszerint számolok. Pl ha 3 rombusz és 2 háromszög van a csúcs körül, akkor 3szor 90 fok plusz 60 fok az 330 fok, a formális szöghiány 30 fok. Ez akkor is ennyi, ha a csúcs körüli igazi szögek pl. 120, 130, 100 és 80 fokok! Na most akkor készítsünk pl. szabálytalan ötszögekből poliédert! Tehát a poliéder csak ötszögeket tartalmazhat, de ezek nem feltétlen egyformák. Egy csúcs körül 3 vagy 4 lap lehet. 3 lapnál a formális szöghiány 36 fok azaz 360 mínusz 3-szor 108 fok, a 4 lapú csúcs formális szöghiánya már negatív, azaz 360-432 azaz -72 fok. Ha a poliéderemnek n db 3-as csúcsa és m db 4-es csúcsa van, akkor a képletünk: n szer 36 mínusz m szer 72 legyen 720 fok. A poliédercsalád legkisebb képviselője a pentagondodekaéder, 12 lappal és 20 csúccsal, 20szor 36 valóban 720 fok. Most jön a kérdés: van-e 13 oldalú, vagy általában páratlan oldalszámú "pentoéder"? Mely k-ra hány nem izomorf k oldalú pentoéder létezik?
|
| Előzmény: [78] Sirpi, 2004-02-27 14:19:35 |
|
| [83] Hajba Károly | 2004-03-01 08:52:29 |
 Kedves László!
Kösz a pontosítást, valóban eggyel elcsúsztattam a számozást.
Nos a 16. feladathoz csak annyit súgok, hogy nem csak téglatestben lehet gondolkodni. A 17. feladathoz talán elegendő volt a korábbi hozzászólás. Remélm ezekután már sikerül legyűrnöd e feladatokat is. :o)
HK
|
| Előzmény: [82] lorantfy, 2004-03-01 08:27:17 |
|
| [82] lorantfy | 2004-03-01 08:27:17 |
 Kedves Károly!
Hát pont a be nem rajzolt takart élekkel volt problémám. Világos, hogy a 17. (=18. az előző hozzászólásodban) feladatnál vannak takart élek amik nincsenek berajzolva, igy ebből arra következtettem, hogy a 16. (=17. az előzőben) feladatnál is vannak.
Sajnos számomra egyenlőre elképzelhetetlen, hogy a 16. elölnézetén látható téglalap alakú bemetszés, ami egy teljesen végigfutó vájatot jelöl, miért nem jelenik meg a felülnézeten végigfutó függőleges vonalként?
A 17-nél most értettem meg, hogy az egész bemetszésnek kivehetőnek kell lennie. Én egy négyzet alapú csonkagúlára gondoltam, ami a kicsúsztatható.
|
| Előzmény: [81] Hajba Károly, 2004-03-01 01:25:37 |
|
| [81] Hajba Károly | 2004-03-01 01:25:37 |
 Kedves László!
Sajnos egyik sem jó. A 17. feladat esetében a bal ábra szerinti elrendezés adódna, de az eredeti feladat szerint nincs megjelenő takart él, azaz nem kell szaggatott vonalat berajzolni.
A 18. feladat rajzánál csak a felületet rajzoltam le, mivel egyrészről éles feltétel volt az egydarabúság és kivehetőség, másrészről a takart él berajzolása nagymértékben segítene a megoldásban. A Te elképzelésedet a jobb ábrára rajzoltam az ábrázoló geometria szabályai szerint.
HK
|
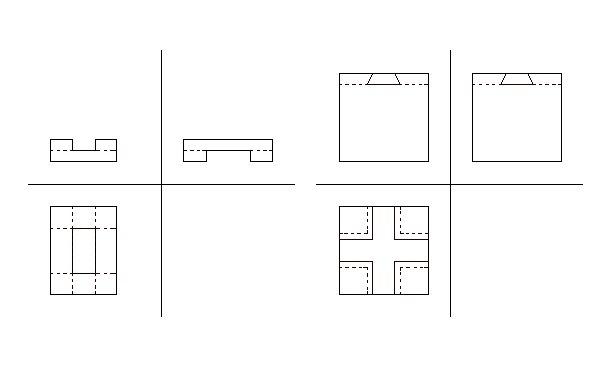 |
| Előzmény: [80] lorantfy, 2004-02-29 23:01:32 |
|
|
| [79] lorantfy | 2004-02-29 22:31:52 |
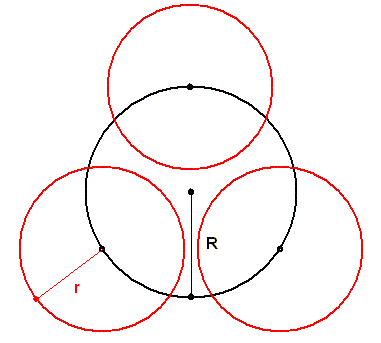
 18. feladat: Mekkor legyen r, hogy a piros körök negyedeljék a nagy kört? (Egyszerű, de nem akartam a "Grafi logikai" topikba tenni.)
|
 |
|
| [78] Sirpi | 2004-02-27 14:19:35 |
 Szia Miklós!
A feladat első részét bevállalom, azaz belátom, hogy nem-lyukas poliéderekre a szöghiány 720o.
Legyen a poliédernek c csúcsa, e éle és l lapja. Az Euler-féle poliéder-tétel szerint nemlyukas poliéderekre c-e+l=2.
Legyenek a poliéder lapjai rendre n1,n2,...,nl oldalúak. Ekkor 2e=n1+n2+...+nl, mert a lapok éleinek számát összeadva minden élt pontosan kétszer számolunk.
A szöghiány c.360o mínusz a poliéderlapok szögeinek összege. Definíció szerint ezt csúcsonként rendezve számoltuk ki, de megtehetjük ezt laponként rendezve is, a sorrend megváltoztatásával az összeg nem változik. Mivel egy ni oldalú lapon a szögösszeg (ni-2)180o, így a teljes szöghiány:
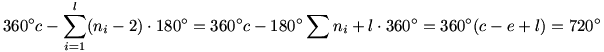
Látható, hogy az eredmény csak c-e+l értékétől függ, amit a test Euler-karakterisztikájának neveznek. "Egyszerű" testekre ez az érték 2, míg pl. tórusszal homeomorf alakzatokra ez az érték 0, ilyenkor a teljes (előjeles) szöghiány is 0o.
S
|
| Előzmény: [77] Kristóf Miklós, 2004-02-26 13:22:22 |
|
| [77] Kristóf Miklós | 2004-02-26 13:22:22 |
 Kedves Mindenki! Most egy kicsit nehéz feladat jön: Egy poliéder egy csúcsa körül valahány lap van, egy lapon a két él valamekkora szöget zár be. Adjuk össze a csúcs körül a szögeket, az eredmény egy konvex poliédernél kisebb mint 360 fok. Amennyivel kisebb, azt szöghiánynak nevezzük. Adjuk össze a poliéder összes csúcsának szöghiányát, egy gömbbel homeomorf poliéder esetén a teljes szöghiány 720 fok kell legyen. Példa: Kocka: 8 csúcs, egy csúcs körül 3x90 fok van, a szöghiány tehát 90 fok. 8 csúcs van, és 8x90 fok az 720 fok. Na, ennyit bevezetőnek. Egy síkbeli kirakómintánál a szöghiány nulla, ezért síkminta. Most jön a feladat: adjunk meg olyan alakzatot, amellyel a szöghiány nagyon pici de nem nulla, pl. kisebb mint 1 fok. Csináljunk ebből az alakzatból minél nagyobb lapszámú "gömböt"! Ez a kirakóminta lokálisan hasonlítson valamely síkbeli kirakómintára.
Ha ez a feladat így egyben túl komplikált, akkor egyszerűsíteni lehet. Lehet olyan minta is, ahol nem egy hanem 2 vagy 3 alakzat szerepel.
Például 3 féle rombuszból csináltam 132 oldalú "romboédert". Ha sikerül valahogy lefotóznom és beszkennelnem, akkor elküldöm a képét.
|
|
| [76] Kristóf Miklós | 2004-02-26 13:08:58 |
 Kedves Onogur! Valóban ezek a négyzet kirakások, azzal a kis kiegészítéssel, hogy az egyes gyűrűk helyettesíthetők a tükörképükkel is, így a 3x3-asra 2, az 5x5-ösre 4, a 7x7-esre 8, és általában 2 az n-iken különböző megoldás lehet.
Az extra elem nélküli téglalap lehetetlenségének bizonyítása majdnem olyan izgalmas, mint egy konkrét megoldás megtalálása!
|
| Előzmény: [71] Hajba Károly, 2004-02-24 12:57:06 |
|
| [75] Hajba Károly | 2004-02-25 23:42:25 |
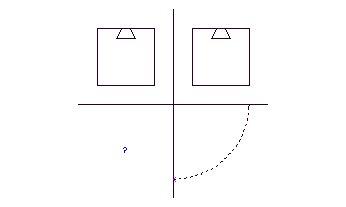
 17. feladat
Egy fakockába betétet véstünk az ábra szerint elől és oldalnézettel. Milyen lehet a felülnézete, ha tudjuk, hogy az egy darabból álló betét kivehető?
HK
|
 |
|
| [74] Hajba Károly | 2004-02-25 21:55:38 |
 16. feladat:
Egy kis "Ábrázoló geometria" - Milyen lehet az ábrázolt idom oldalnézete?
HK
|
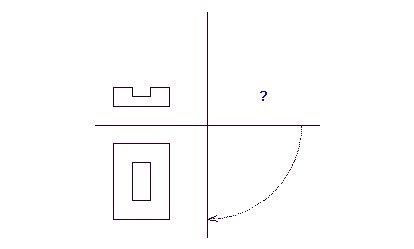 |
|
| [73] Csimby | 2004-02-25 10:43:41 |
 Szeretném kijavítani magamat, ugyanis 10 db. négyzetre mégiscsak találtam egy megoldást!
|
|
| [72] Csimby | 2004-02-24 20:52:49 |
 Kedves Onogur!
A feladatot először itt láttam: http://www.stetson.edu/ efriedma/touchingn/ , itt 4-re, 12-re és 14-re van megoldás, de a többi esetről semmmit sem mond. Én találtam megoldást minden páros n-re, azt pedig, hogy a páratlanok miért nem jók nagyon könnyű belátni. Az, hogy 6,8,10 -re miért nem jó szerintem nehezebb dió, tulajdonképpen csak 6-re néztem meg, mert nem találtam egyszerű módszert, de amit kitaláltam szerintem működik 8-ra és 10-re is. A feladatot egyébként úgy gondoltam, hogy összefüggő legyen az alakzat és a csúcsokban történő érintés is érintésnek számítson. Most lelőttem a poént, hogy mikor van megoldást, de a konstrukciókat és bizonyításokat attól még ki lehet találni, és elképzelhető, hogy 8,10-re van megoldás csak én nem találtam.
|
|
| [71] Hajba Károly | 2004-02-24 12:57:06 |
 Kedves Miklós!
A 3*3, 5*5, 7*7, ... négyzet kirakása nagyságrendekkel könnyebb, mint az eredeti feladatod, főleg László képei után. Érdekes lenne a 4*4, ... 2n*2n, négyzeteket kirakni a kiegészítő négyzet számoságának bizonyos korlátozásával (,de ebbe még bele kellene mélyedni :o).
Szóval az az érzésem az eredeti feladattal kapcsolatban, hogy nagyobb valószínűséggel lehetne bizonyítani a kirakás lehetetlenségét, mint kirakni. De hát ez csak egy érzés.
S csak illusztrációnak az első bekezdésbeli kirakások:
|
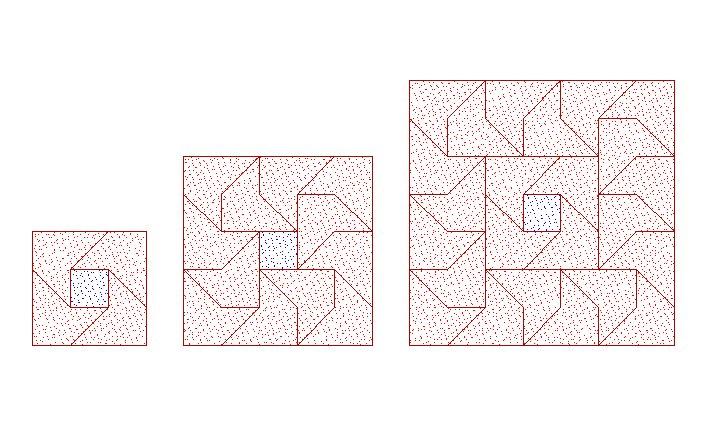 |
| Előzmény: [67] Kristóf Miklós, 2004-02-24 10:56:07 |
|
| [70] Hajba Károly | 2004-02-24 11:03:55 |
 Kedves Csimby!
Újabb érdekes feladatokat kotortál elő valahonnan.
Tehát, ha jól értem, akkor egységnégyzeteket kell lehelyeznünk.
Ha 4 db négyzetet úgy helyezek el, hogy az egy nagyobb négyzetet alkosson, akkor elvileg mind a 4 négyzet 3 másikat érint. Így elvileg minden n*4 négyzetet le lehet helyezni, hogy 3 másikat érintsen, feltéve, hogy nem egybefüggő alakzatot kell alkotni a végeredménynek.
Tehát a fenti hozzászólásomban 3 pontosítási eset is van:
(1) egységnégyzet; (2) "keresztbe érintés" sarok a sarokkal érintés-e; (3) a végeredmény lehet-e széteső vagy egybefüggőnek kell lennie?
HK
|
| Előzmény: [65] Csimby, 2004-02-23 23:17:38 |
|
| [69] Kristóf Miklós | 2004-02-24 11:03:10 |
 Kedves Lorantfi! Köszönöm az ábrát, igen, ez az az alakzat. Az első ábra prezentálja azt az esetet, amikor egy exta elemet, egy négyzetet is használok. Az eredeti feladatban viszont extra elem nélkül kell megcsinálni a téglalapot. Az alakzat tükörképe is használható. Úgy érzem, vagy nincs megoldás, vagy ha van akkor nagyon nagy.
|
| Előzmény: [60] lorantfy, 2004-02-18 13:46:01 |
|
|
| [67] Kristóf Miklós | 2004-02-24 10:56:07 |
 Kedves Géza! A feladat tőlem származik, nem emlékszem hogy valaha is láttam volna máshol. Természetesen fel lehet adni pontversenyben is, de azzal a megjegyzéssel hogy semmi se garantálja hogy létezik megoldás, illetve lehet hogy a legkisebb megoldás is többezer elemből áll. Én olyan versenyként adnám fel, ahol nem időre mérik a megoldást, hanem az nyer aki előbb beküld egy működő megoldást, és ezután még azok kapnak pontot akik ettől eltérő új megoldást küldenek be. A versenynél meg lehet említeni a nevem, hogy ez tőlem származik. Még nagyon sok feladatot tudok. Pl. feladat lehet aperiodikus de szabályos minták kirakása ezzel az alakzattal az egész síkon.További feladat lehet olyan kirakóminta, ahol ez az alakzat egy másikkal együtt szerepel párban. Pl. ha még egy egységnégyzet is megengedett, akkor lehet 3x3, 5x5, 7x7... stb négyzet kirakása. Milyen más extra alakzat jöhet szóba?
|
 |
| Előzmény: [63] Kós Géza, 2004-02-19 11:41:11 |
|
| [66] Csimby | 2004-02-23 23:23:30 |
 Bocsánat, kifelejtettem, hogy a négyzetek legyenek egybevágóak!
|
|
| [65] Csimby | 2004-02-23 23:17:38 |
 15.feladat El lehet-e helyezni 6,8,10 db. négyzetet a síkban úgy, hogy mindegyik pontosan 3 másikat érintsen?
El lehet-e helyezni páratlan sok négyzetet a síkban úgy, hogy mindegyik pontosan 3 másikat érintsen?
El lehet-e helyezni 4,12,14,16... db. négyzetet a síkban úgy, hogy mindegyik pontosan 3 másikat érintsen?
|
|
| [64] lorantfy | 2004-02-22 22:27:05 |
 Kedves Géza és Fórumosok!
Desargues tétele: Ha két  csúcspontjait összekötő egyenesek: AA1, BB1 és CC1 egy S pontban metszik egymást, akkor a két csúcspontjait összekötő egyenesek: AA1, BB1 és CC1 egy S pontban metszik egymást, akkor a két  megfelelő oldalegyeneseinek metszéspontjai egy egyenesre esnek. megfelelő oldalegyeneseinek metszéspontjai egy egyenesre esnek.
A tétel megfordítása: Ha két  megfelelő oldalegyeneseinek metszéspontjai egy egyenesre esnek, akkor a megfelelő csúcspontokat összekötő egyenesek: AA1, BB1 és CC1 egy pontban metszik egymást. megfelelő oldalegyeneseinek metszéspontjai egy egyenesre esnek, akkor a megfelelő csúcspontokat összekötő egyenesek: AA1, BB1 és CC1 egy pontban metszik egymást.
Mi köze van a tétel megfordításásnak ahhoz, hogy a  súlyvonalai egy ponban metszik egymást? Az ábráról ez már leolvasható. súlyvonalai egy ponban metszik egymást? Az ábráról ez már leolvasható.
Ha a két  megfelelő oldalegyeneseinek metszéspontjai ideális pontok - vagyis ha az oldalegyenesek egymással párhuzamosak - a tétel akkor is igaz. A megfelelő oldalegyeneseinek metszéspontjai ideális pontok - vagyis ha az oldalegyenesek egymással párhuzamosak - a tétel akkor is igaz. A  középvonalai pedig nyilván párhuzamosak az oldalakkal. középvonalai pedig nyilván párhuzamosak az oldalakkal.
(A tétel a Hajós-ban: Ha két háromszög pontra nézve perspektív, akkor egyenesre nézve is perspektív és fordítva)
|
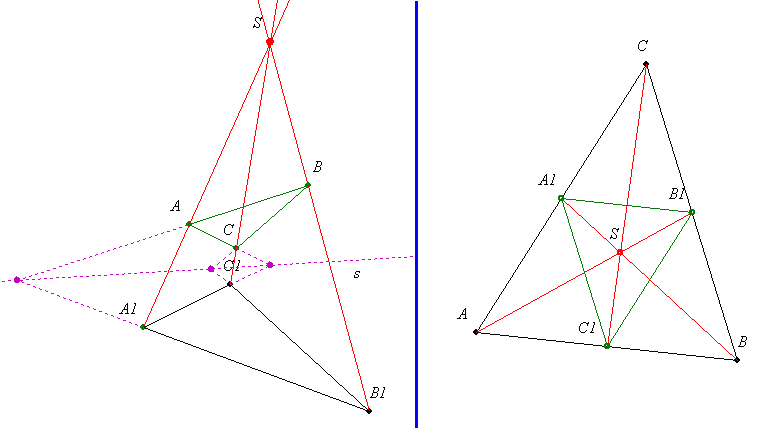 |
| Előzmény: [58] Kós Géza, 2004-02-16 13:51:32 |
|
|
| [62] BohnerGéza | 2004-02-18 16:06:33 |
 Kedves Fórumosok!
Igazán nem László [56] és Géza [58] bosszantására ( sőt ha nem lesz más jelentkező, akkor az általuk várt megoldást is megadom), hanem tanulságos volta miatt írom a következőket:
Amíg egyenesek párhuzamosságáról, metszéspontjukról van csak szó egy feladatban, célszerű lehet ferdeszögű koordinátarendszert használni. A krsz-t kezdőpontja és alapvektorai határozzák meg, melyekre ilyenkor elég, ha a nem párhuzamosak feltétel teljesül. A 14. feladat [46] esetén az A-t véve kezdőpontnak, az AB-t és AD-t véve alapvektornak a következő ábra alapján lehet számolni.
Ajánlom a módszert a 10.C. feladat [45] ábráját tekintve megoldására is. Ott célszerű a D-ből induló A ill. C felé mutató egységvektorokkal indulni. ( D(0;0), A(b;0), C(0;c), B(b;c), X(b;a), ... ) Igaz, így a megoldás annyira egyszerű lesz, hogy az már nem is szép, de a versenyen gyorsan, bemelegítésként megoldhatunk esetleg így egy feladatot.
|
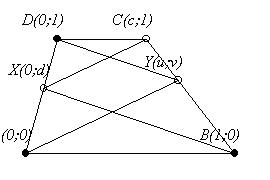 |
|
|
|
| [59] Kristóf Miklós | 2004-02-18 12:55:21 |
 Kedves Mindenki! Lehet-e téglalapot kirakni az alábbi alakzatból?
Bocs, nem tudom felrajzolni.Mindent egy sorba ír ez. Így kell rajzolni: Két lépés le, egy lépés jobbra, egy lépés jobbra fel, egy lépés balra, egy lépés balra fel. Ez tehát egy konkáv ötszög. A kirakást természetesen négyzethálós papíron kell elképzelni.
|
|
| [58] Kós Géza | 2004-02-16 13:51:32 |
 Csak egy apróság a projekítv geometria kedvelőinek.
Azt, hogy a súlyvonalak egy ponton mennek át, a Desargues-tétel megfordításával érdemes (és érdekes) kapcsolatba hozni. (Ezt is a feleségemtől tanultam. :-))
|
| Előzmény: [54] BohnerGéza, 2004-02-10 23:50:33 |
|
| [57] BohnerGéza | 2004-02-15 21:31:44 |
 Kedves László és Fórumosok!
László észrevétele teljesen jogos, nem egyszerű a javasolt megoldás, így további útmutatást adok. ( Nem gondoltam végig, ráadásul elszámoltam az Y vektort. )
A megoldás lényege a következő: A-ból B-be és D-be mutató vektorok és a gamma ismeretében a trapéz adott, a delta meghatározza X-et. Az AY párhuzamos XC feltétel meghatározza Y-t, tehát bétát is (deltától függ). Ehhez kihasználjuk majd, hogy ha pD=qB, akkor p=q=0, mivel d és B nem egyirányú vektorok. A béta ismeretében igazolható a BX párhuzamos YD. A megoldás befejezését most is az érdeklődőkre bízom. Jóval egyszerűbb a számolás, ha a helyvektorok kezdőpontjának a szárak metszéspontját vesszük, ezt is javaslom végigszámolni azoknak, akik még keveset foglalkoztak vektorokkal.
|
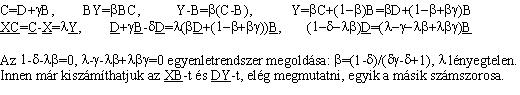 |
|
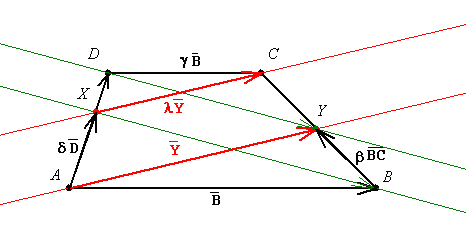
| [56] lorantfy | 2004-02-13 10:48:13 |
 Kedves Géza és Fórumosok!
Természetesen bármilyen módszerrel adott megoldást szivesen látok a 14. feladatra. Azért szeretném ha megoldaná valaki a Papposz tétel felhasználásával is, hogy a [44] és [45] hozzászólásom ne legyen hiábavaló.
Persze Géza megoldási javaslatát is be kellene fejeznie valakinek...(Remélem Géza nem sértődsz meg érte, de szerintem a bafejezés nem mindenkinek nyilvánvaló!) Segítségül egy ábra:
|
 |
| Előzmény: [55] BohnerGéza, 2004-02-13 00:38:12 |
|
| [55] BohnerGéza | 2004-02-13 00:38:12 |
 Mindenkitől elnézést kérek, de az 54. hozzászólásban sikerült második 14. feladatot összehoznom, ezért az eredetire, a 46-ban szereplőre mutatok egy megoldási lehetőséget. Tudom, a feladat kitűzője nem erre a módra gondolt, de így is lehet. Ajánlom mindazoknak, akik a vektorokkal való számolást még nem "érzik".
A 46. hozzászólásban szereplő ábra jelöléseit használjuk.
|
 |
|
| [54] BohnerGéza | 2004-02-10 23:50:33 |
 (Téma: Ahhoz, hogy három nem párhuzamos egyenes egy pontban metszi egymást elég megmutatni, hogy van olyan pont, melyet tükrözve az első, a tükörképet a második, majd a harmadik egyenesre, visszajutunk az eredeti pontba.
Ezt használva könnyen megmutatható, hogy a háromszög oldalfelezőmerőlegesei egy pontban metszik egymást. Ismerve az – még nem biztosan létező, hiszen most akarjuk belátni, hogy van középpontjuk – érintőkörök tulajdonságait, a szögfelezőkhöz – három belső, vagy két külső és a harmadik belső – is találunk ilyen pontot. A magasságvonalakkal kapcsolatban:
14. feladat: Jelöljük az ABC háromszög magasságegyeneseit a-val, b-vel, c-vel, a és c metszéspontját M-mel, az M középpontú B-n áthaladó kört k-val, a béta szögfelezőjének k-val való metszéspontját P-vel. Mutassuk meg, hogy P segítségével igazolható, hogy a magasságegyenesek egy pontban metszik egymást.
A súlyvonalakkal kapcsolatban még nem jutottam biztos eredményre, de:
15. feladat: Az ABC háromszögben legyen p az alfa belső, q és r a béta ill. gamma külső szögfelezője, S ezek metszéspontja, F az S-ből a BC-re állított merőleges talppontja. Q-t és R-t az AF-re F-ben állított merőleges metszi ki q-n ill, r-en. Bizonyítandó, hogy F a PQ felezőpontja!
A feladat bizonyítása megy, csak azt nem látom, hogy - a fenti feladatban - abban a PQR háromszögben, melynek S a súlypontja az A segítségével belátható-e, hogy a súlyvonalak egy pontban metszik egymást.
A témával kapcsolatban szívesen fogadok segítséget (irodalom, feladatok).
|
|
| [53] Csimby | 2004-02-10 22:21:39 |
 Igen Onogur erre gondoltam, de sajnos ha van is még ilyen eset, túl sok háromszöget kell elhelyezni.
Talán érdekes lehet, a természet hogyan old meg a hasonló feladatot: (http://hydra.nat.uni-magdeburg.de/packing/packing.html)
|
 |
|
| [52] Hajba Károly | 2004-02-10 00:40:33 |
 Kedves Csimby!
Ha jól értelmeztem a 13/b feladatodat, akkor arra lennél kiváncsi, hogy létezik-e még olyan a amire s egész. Én a=16-ra s=2,976+ eredményt hoztam ki, míg a=17-et nem sikerült s=3-ba belerakni. Így, ha létezik, az magasabb régiókban található.
HK
|
 |
| Előzmény: [49] Csimby, 2004-02-07 19:09:25 |
|
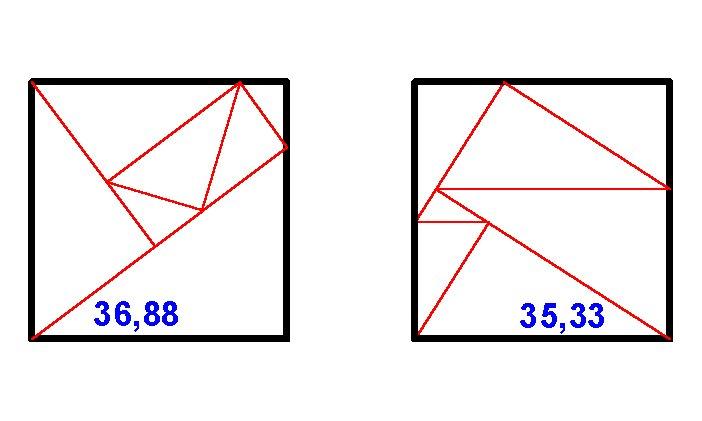
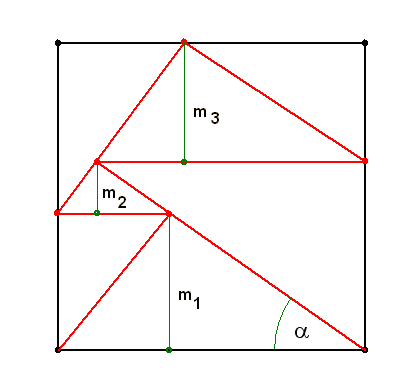
| [51] Hajba Károly | 2004-02-09 00:32:26 |
 Kedves Osztogatók!
Közreadom a 12. feladatra a saját megoldásomat, az alábbi megjegyzésekkel: (1) Úttörőbecsületszavamra kijelentem, hogy nem kukkoltam más honlapokra :o) (2) mivel több napig csak ritkán kerültem gépközelbe, így csak most tudtam a feladattal komolyabban foglalkozni. (3) Megoldást csak iteratív módszerrel sikerült készítenem (4) de cserében felszerkesztettem László változatát is a szögméréshez ( ). ).
 =36,88445849... =36,88445849...  =35,33... =35,33...
S az ábrák:
|
 |
| Előzmény: [37] Csimby, 2004-02-04 19:59:04 |
|
| [50] lorantfy | 2004-02-07 22:12:38 |
 Kedves Csimby!
Kösz a jó feladatokat. A 13-ast láttam a Stetson-on, ezt nem találtam meg, igy kénytelen voltam próbálkozni. Megszerkesztettem, és így már valamivel meggyőzőbb.
|
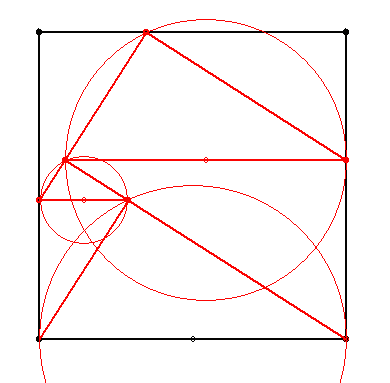 |
| Előzmény: [49] Csimby, 2004-02-07 19:09:25 |
|
| [49] Csimby | 2004-02-07 19:09:25 |
 Kedves Lorantfy!
Szerintem jó a megoldásod, másik két megoldás található a feladatra a következő címeken: http://www.stetson.edu/~efriedma/tis/iso01.gif http://www.stetson.edu/~efriedma/tis/iso11.gif
Kedves Onogur!
Ez is jó, gratula! 13.b feladat Vajon a 7-en kívül más a darabszámra is igaz, hogy a db egység oldalú szabályos háromszöget el lehet helyezni egy olyan négyzetben amelynek oldalhossza a többszöröse (ennél kissebb oldalhosszú négyzetben viszont nem, persze ezt nem kell bizonyítani, nekem elég ha "úgy tűnik")? (a=15-ig "úgy tűnik" nincsen más ilyen lásd.: http://www.stetson.edu/~efriedma/triinsqu/)
|
|
| [48] lorantfy | 2004-02-07 14:10:38 |
 12. feladat megoldása: Jól néz ki, de nem biztos, hogy létezik! Ha van kedve valakinek számoljon utánna, lehet-e mindegyik háromszög derékszögű az ábrán!
|
 |
| Előzmény: [37] Csimby, 2004-02-04 19:59:04 |
|
|
| [46] lorantfy | 2004-02-07 00:15:18 |
 14. feladat: Vegyük fel az ABCD trapéz AD szárán az X, BC szárán az Y pontot.
Bbh. ha AY párhuzamos CX egyenessel, akkor DY is párhuzamos BX egyenessel !
|
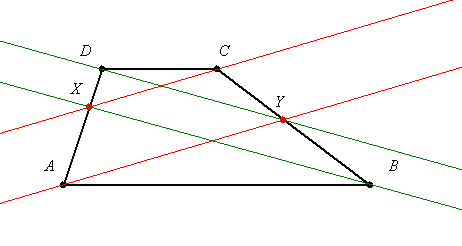 |
| Előzmény: [45] lorantfy, 2004-02-07 00:02:03 |
|
| [45] lorantfy | 2004-02-07 00:02:03 |
 Kedves Fórumosok!
Csak most jön a 10.c) feladat megoldása: A Papposz tételt szeretnénk alkalmazni, tehát 3-3 egy egyenesre eső pontot kell keresnünk. Mivel azt kell bizonyítanunk, hogy AY és CX egyenesek C3 pontban, a szögfelezőn metszik egymást, így a 2-2 pont már meg is van és kell még 1-1 pontot keresnünk az AB illetve BC egyeneseken, úgy, hogy a keletkező két új metszéspont a szögfelezőn legyenek. Ekkor a tételből már következne, hogy C3 is a szögfelezőn van.
Hát nem lesz könnyű megtalálni a hiányzó két pontot, minthogy a végtelenben vannak. Tehát csak párhuzamost kell húznunk X pontból BC-vel és Y pontból AB-vel és ezek metszéspontja lesz C2. A C1 pont pedig egyszerűen D. Ez a két pont nyilván rajta van a szögfelezőn, hiszen egy rombusz szemközti csúcsai, így aztán a Papposz tételből következően C3 pont, AY és CX egyenesek metszéspontja is a szögfelezőre esik.
Sajnos ennyiből még mindig nem úsztátok meg. Most Nektek kell bizonyítani! Mégpedig azt, hogy tudjátok alkalmazni Papposz tételét egy másik feladatban!
|
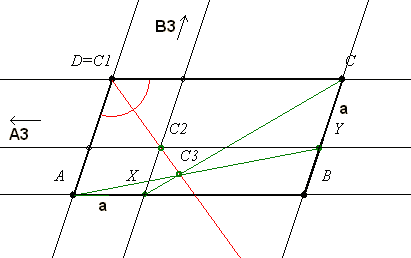 |
| Előzmény: [44] lorantfy, 2004-02-06 23:11:33 |
|
| [44] lorantfy | 2004-02-06 23:11:33 |
 Kedves Csillag és Fórumosok!
Már egyszer felvetődött, hogy ez a feladat Papposz tételére vezethető vissza. Akkor rajzoltam egy ábrát és nem láttam hogyan. Most, hogy újra előjött rászántam egy kis időt és most megpróbálom úgy leírni, hogy azoknak is érthető legyen, akik nem akarják átnyálazni a Hajós könyvet.
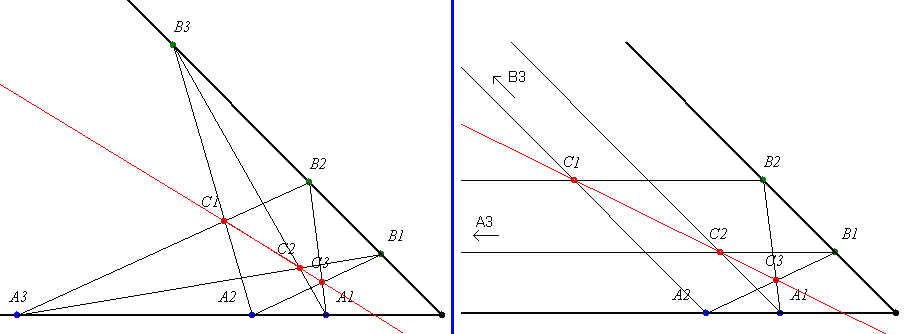
10.c) feladat megoldása Nézzük először mit állít Papposz tétele: Ha A1, A2, A3 pontok egy egyenesen vannak és B1, B2, B3 pontok is egy egyenesre esnek és A1B2 metszéspontja A2B1 egyenessel C3, A1B3 metszéspontja A3B1 egyenessel C2, A2B3 metszéspontja A3B2 egyenessel C1 akkor C1, C2, C3 pontok is egy egyenesen vannak.
Ha valaki csak ez alapján próbálja alkalmazni a tételt a feladatra nehezen fog menni. Ahhoz tudnia kell még, hogy a tétel "elfajuló" esetben is igaz, pl. akkor, ha A3 és B3 pontok a végtelenben vannak (ideális pontok). Ilyenkor a jobb oldali ábrán látható, szögszárakkal párhuzamos egyenesek metszéspontjaként keletkezik C1 és C2 pont. Na ez az eset kell nekünk a paralellogrammában!
|
 |
| Előzmény: [29] Csillag, 2004-02-02 20:05:04 |
|
|
| [42] Csillag | 2004-02-05 23:52:31 |
 Kedves Attila!
Igazad van, félreérthető voltam. Egy néhány éve megírt cikk (Martin Gardner: Penrose-csempézés + +) foglalkozik ezzel a témával és tisztázza a fogalmakat. Azok a csempézések, amikkel Penrose foglalkozott, olyan elemekből épültek fel, amelyekből csak nem periodikus csempézés készíthető. A Hajba Károly/Onogur által megadott csempével viszont készíthető periodikus csempézés is.
"A legjelentôsebb megoldatlan probléma persze az, hogy van-e egyetlen alakzat, mellyel nem periodikusan csempézhetô a sík. A legtöbb szakértô szerint nincs, de senki nem jutott még csak közel sem a bizonyításhoz. Még azt sem bizonyították, hogy ha van ilyen csempe, akkor az nem lehet konvex."
Remélem a cikk érthetőbb lesz, mint az én megfogalmazásaim:)
GB
|
| Előzmény: [41] jenei.attila, 2004-02-05 09:53:23 |
|
| [41] jenei.attila | 2004-02-05 09:53:23 |
 Kedves Csillag!
Most egy kicsit összezavartál aperiodikus parkettázás ügyében. Legutóbbi hozzászólásodból számomra az derül ki, hogy jelenleg legalább két csempe kell ehhez, ahogy Penrose is csinálta. Ugyanakkor Onogur azt állítja, hogy az általa megadott egyetlen csampével is lehetséges az aperiodikus parkettázás. Most akkor mi az igazság?
|
| Előzmény: [38] Csillag, 2004-02-04 21:28:41 |
|
| [40] Csimby | 2004-02-05 09:07:34 |
 Semelyik kettő ne legyen egybevágó!
|
|
| [39] lorantfy | 2004-02-05 08:33:06 |
 Kedves Csimbi!
A 12. feladathoz annyi lenne a kérdésem, hogy a 7 háromszög között nem lehetnek egybevágóak, vagy csak annyi a kikötés, hogy nem lehet mind egybevágó?
|
| Előzmény: [37] Csimby, 2004-02-04 19:59:04 |
|
| [38] Csillag | 2004-02-04 21:28:41 |
 Tisztelt Érdeklődők!
Nem Penrose foglalkozott először a sík nem periodikus csempézésével. Eredetileg 25000 körüli volt a sík nem periodikus lefedéséhez használt különböző csempék száma, majd 100. Ezt a számot Rafael Robinson 6-ra javította, és azon dolgozott, hogy minimális számú különböző csempével fedhesse le a síkot (nem periodikusan). Penrose ezután jött elő egy szintén 6 csempéből álló halmazzal, amit később leegyszerűsített 2 eleműre. Roger Penrose-ról pl. a következő könyvben olvashatunk: Staar Gyula: Matematikusok és teremtett világuk, Vince Kiadó
GB
|
| Előzmény: [36] Hajba Károly, 2004-02-04 10:38:02 |
|
| [37] Csimby | 2004-02-04 19:59:04 |
 12. Feladat
Osszunk fel egy négyzetet 7 db hasonló, de nem egybevágó háromszögre.
13. Feladat
Pakoljunk bele 7 db 1/2 oldalhosszúságú szabályos háromszöget egy egység oldalú négyzetbe, átfedések nélkül.
|
|
| [36] Hajba Károly | 2004-02-04 10:38:02 |
 Kedves Attila!
Igen Penrose jött ki előszőr ilyenekkel, elő kellene keresnem a régi KöMaL számokat, de talán az archívumba már fel van rakva a '70-es évek vége, abban foglalkoztak e témával.
A matematikai hátterében nem vagyok mélyen benne, csak autodidakta módon és szintem, de szakmám miatt folyamatosan "edzésben tartom" a térlátásomat, így a "parkettázás" a hobbimmá vált. Továbbá egy jó kis CAD rendszer a kezem alá dolgozik, tehát az elképzelt megoldásokat könnyen ki is próbálhatom. Az eredményeket magad is láthatod korábbi képeimnél.
HK
|
| Előzmény: [35] jenei.attila, 2004-02-04 10:13:38 |
|
| [35] jenei.attila | 2004-02-04 10:13:38 |
 Kedves Károly!
Nagyon szép a 4. feladatra adott megoldásod. A középponton átmenő körívekkel való felosztásig én is eljutottam, aztán valami olyasmire gondoltam, hogy bizonyos idomok egyes határvonalait kellene elhagyni, olyanokat amelyek a középpontot tartalmazzák. Így egyfajta félig nyílt alakzatok jöhettek volna létre, de tovább nem jutottam, meg amúgy sem lett volna az "igazi" megoldás.
A parkettázós témában úgy látom otthon vagy, a legutóbbi hozzászólásodban ha jól értem ún. aperiodikus parkettázást adtál meg. Úgy tudom először ilyet Roger Penrose adott meg, nem kis meglepetést okozva ezzel matematikus körökben. Az ő parkettázása ha jól emlékszek két különböző alakzatot használ. Ezzel kapcsolatban mit tudsz, vagy ha valamit rosszul értettem, kérlek javíts ki.
Üdvözlettel: Jenei Attila
|
| Előzmény: [30] Hajba Károly, 2004-02-03 13:06:53 |
|
| [34] Hajba Károly | 2004-02-04 00:58:26 |
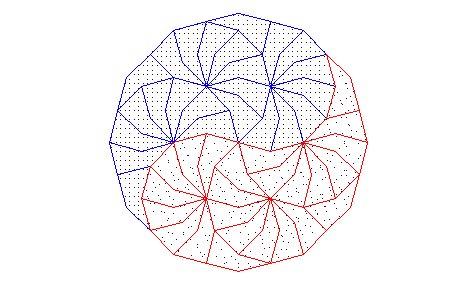
 Tovább gombolyítom e téma és idom fonalát: (1) Ha jól emlékszem ilyen idomokról volt kömalos feladat és cikk is anno az "én időmben". (2) Ezen idommal, ha jól sejtem, végtelenféleképpen lehet lefedni a síkot úgy, hogy a keletkezett minta nem transzformálható át önmagába. (3) Sok érdekes szólóminta is kialakítható belőle, például László említette Jin-Jang is:
|
 |
| Előzmény: [33] Hajba Károly, 2004-02-04 00:47:19 |
|
|
| [32] lorantfy | 2004-02-03 23:02:41 |
 Kedves Károly és Fórumosok!
A pajzs alakú darabnak két domború és egy homorú oldala van. Ha az egyik domború oldalt egyenes szakasszal helyettesítjük, akkor lefedhető a sík hézagmentesen. Nem tudom erre gondoltál-e vagy valamilyen más formát találtál ki? Mindenesetre én még nem láttam ilyen térburkolatot. Javasolhatnánk valamelyik gyártó cégnek!
(Csak két varit rajzoltam, mert az Euklides progival kicsit körülményes ezt szerkeszteni)
|
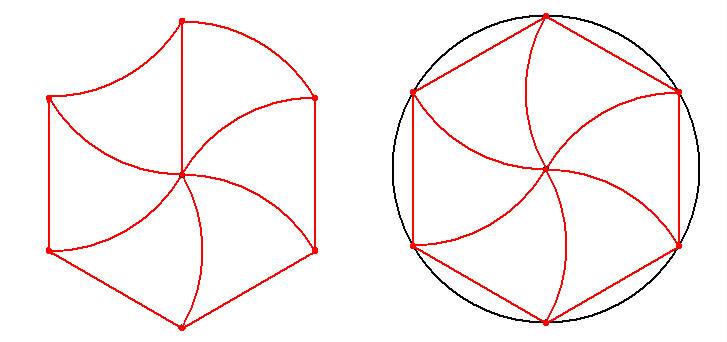 |
| Előzmény: [31] Hajba Károly, 2004-02-03 13:13:24 |
|
| [31] Hajba Károly | 2004-02-03 13:13:24 |
 11. feladat:
A 4. feladat megoldásának idomát kis módosítással át lehet-e alakítani úgy, hogy ennek és tükörképének felhasználásával a teret hiánytalanul le tudjuk fedni, akár többféle elrendezéssel is?
Hajba Károly
|
|
