|
| [1548] Fálesz Mihály | 2012-05-02 09:58:01 |
 Vannak speciális esetek, amikor egy sokadrendű görbe és egy kör metszéspontja véletlenül mégis szerkeszthető.
Jó lenne egy olyan esetet kipreparálni, amikor a megadott adatok "szépek", de az eredményben valami jól ismert, nem szerkeszthető mennyiség szerepel.
|
| Előzmény: [1547] BohnerGéza, 2012-05-02 02:11:52 |
|
| [1547] BohnerGéza | 2012-05-02 02:11:52 |
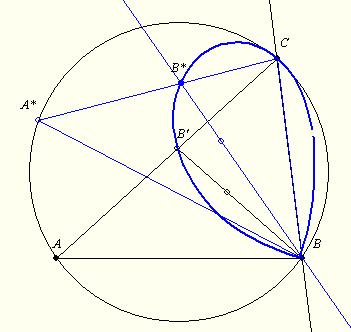
 Egy példa, ahogyan a 178. feladat nem szerkeszthető:
(A BC oldal és a körülírt kör szerkeszthető.)
Tfh az ABC a szerkesztendő háromszög, ekkor a körülírt körén mozgó A* pont és a szerkesztőprogram segítségével kirajzolható az A*BC háromszög B* pontjainak nyomvonala. B* a B-ből induló szögfelező másik vége.
A B* nyomvonala nem másodrendű, így nem szerkeszthető.
A nyomvonal ismeretében B* számára meglenne a két szükséges vonal. (A másik a B kp-ú, az adott szögfelező sugarú kör.)
|
 |
| Előzmény: [1546] Konkoly Lászlóné, 2012-04-24 22:36:53 |
|
| [1546] Konkoly Lászlóné | 2012-04-24 22:36:53 |
 [1546] A 25. feladathoz hasonló szerkesztési feladat:
178.feladat: Szerkesszük meg a háromszöget (vagy mutassuk meg, hogy nem lehetséges), ha adott a háromszög egy oldala (a), a vele szemközti szög (alfa) és nem az alfához, mint a 25. feladatban, hanem egy másik szöghöz (pl. a bétá-hoz) tartozó szögfelező hossza.
|
|
| [1545] HoA | 2012-03-26 14:18:01 |
 "Úgy látom, leszoktunk a feladatok sorszámozása." (áról) Ne tegyük. A 174. volt szerintem az utolsó számozott. Legyen [1531] a 175. , [1537] a 176. és most jöjjön a
177. feladat: Az ABCD húrnégyszög csúcsai által meghatározott ABC, BCD, CDA, DAB háromszögek beírt köreinek középpontja legyen OD , OA , OB , OC . A CD oldalegyenest messe ODOA E-ben, OCOB F-ben . Bizonyítsuk be, hogy ABEF húrnégyszög.
|
| Előzmény: [1531] BohnerGéza, 2011-12-31 01:11:20 |
|
| [1542] Danesz | 2012-03-19 19:18:17 |
 Ja, a kötözködők kedvéért: A definícióban nincs szó síklapokról :P
|
|
| [1541] Danesz | 2012-03-19 19:12:04 |
 A tér a 3-dimenziós euklideszi tér. Ismétlem a definíciót kicsit másképpen: Az A halmaz átdarabolható a B halmazba, ha Az A halmaz felbontható véges sok olyan A1, A2, ..., An diszjunkt halmazra (vagyis az Ai halmazok uniói kiadják A-t), hogy ezeket az Ai halmazokat valamilyen (lehet, hogy minden i-re különböző) mozgással átvihetünk olyan Bi (természetesen szintén n darab) diszjunkt halmazba, hogy a Bi-k egyesítése kiadja B-t. Remélem elég részletes és pontos. Ja, és a mozgás az irányítástartó izometria (legjobb tudásom szerint)
|
| Előzmény: [1540] Fálesz Mihály, 2012-03-18 13:13:44 |
|
| [1540] Fálesz Mihály | 2012-03-18 13:13:44 |
 Nem egyértelmű, hogy mi a kérdés. Mit nevezel "átdarabolás relációnak"? Mi a "tér"? Hány darabra vághatunk? Csak véges sokra, vagy megszámlálható sokra? Csak síklapokkal vághatunk, vagy diszjunkt részhalmazokra bontunk?
Végtelen sok diszjunkt darab megengedése esetén elismételheted a Cantor-Bernstein-Schröder tétel valamelyik bizonyítását.
|
| Előzmény: [1536] Danesz, 2012-03-17 18:42:39 |
|
| [1539] Fálesz Mihály | 2012-03-18 13:05:06 |
 Az egy egyenesen levő szakaszok arányai között több összefüggést találhatsz akár közvetlenül, akár a Menelaosz-tétel felírásával.
Az ADC, BEC, APE, BPD egyeneseken a különböző szakaszok arányát kifejezheted a területekkel, például 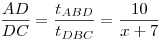 . .
Ezekből összerakhatod a megoldást...
|
| Előzmény: [1537] Sudárné, 2012-03-18 09:32:48 |
|
|
| [1537] Sudárné | 2012-03-18 09:32:48 |
 A feladat a következő: Egy háromszög egy-egy oldalán vegyünk fel egy-egy tetszőleges pontot (jelöljük mondjuk D-vel és E-vel) Ezeket a pontokat kössük össze a velük szemközt lévő háromszög csúcsával. A háromszög így négy részre bomlott, három háromszögre és egy négyszögre, A három háromszög területét ismerem, kérdés a négyszög területe.
Az ábrán találhatóak a további adatok.
|
 |
|
| [1536] Danesz | 2012-03-17 18:42:39 |
 Üdv mindenkinek! Segítenétek egy feladat kidolgozásában? Bizonyítandó, hogy a tér részhalmazain értelmezett átdarabolás relációra igaz, hogy ha A átdarabolható B egy részhalmazába, és B átdarabolható A egy részhalmazába, akkor A átdarabolható B-be. (A átdarabolható B-be, ha létezik az A=U(A(i)) véges diszjunkt felbontás és B=U(B(i)) véges diszjunkt felbontás, hogy A(i) mozgással átvihető B(i)-be)
[U az unió jele]
|
|
|
|
| [1533] BohnerGéza | 2012-01-11 00:58:59 |
 Mint HoA megoldásából is látszik, ha P közelebb van a vezéregyeneshez mint a fókuszpont, de P nincs a tengelyen, akkor is igaz az 1531-beli állítás. Ekkor a nagyítás aránya negatív.
|
| Előzmény: [1532] HoA, 2012-01-08 16:41:15 |
|
| [1532] HoA | 2012-01-08 16:41:15 |
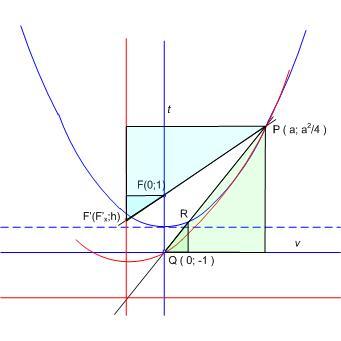
 Nem nagy a tolongás. Egy mechanikus bizonyítás, mely talán kedvet vagy ötletet ad egy szemléletesebbhez: Válasszuk úgy a koordinátarendszer egységét, hogy a parabola egyenlete 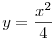 legyen. Ekkor F koordinátái ( 0;1) , v és t metszéspontja Q( 0;-1) . Legyen legyen. Ekkor F koordinátái ( 0;1) , v és t metszéspontja Q( 0;-1) . Legyen 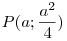 , ahol a feltétel szerint a>2 . A PQ egyenes és a parabola második metszéspontjára ( R ) felírt, x-re adódó másodfokú egyenletből (x-a) kiemelhető, a másik megoldás , ahol a feltétel szerint a>2 . A PQ egyenes és a parabola második metszéspontjára ( R ) felírt, x-re adódó másodfokú egyenletből (x-a) kiemelhető, a másik megoldás 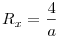 . A nagyítás során R képe Q, F képe F' ,ennek ordinátája legyen h. A lineáris méretek azonos nyújtása miatt a zöld illetve kék hasonló háromszögek hasonlósági aránya megegyezik: . A nagyítás során R képe Q, F képe F' ,ennek ordinátája legyen h. A lineáris méretek azonos nyújtása miatt a zöld illetve kék hasonló háromszögek hasonlósági aránya megegyezik: 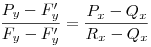 ; ; 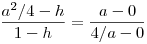 ; ; 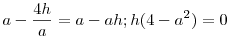 , ebből pedig a > 2 miatt h=0 . , ebből pedig a > 2 miatt h=0 .
|
 |
| Előzmény: [1531] BohnerGéza, 2011-12-31 01:11:20 |
|
| [1531] BohnerGéza | 2011-12-31 01:11:20 |
 jonas [1530]: Azért ne ijesszük el az olvasókat. Megy egyszerűbben is! HoA leírásából nem következik?
(Úgy látom, leszoktunk a feladatok sorszámozása.) Egy másik feladat:
|
 |
|
|
|
| [1528] HoA | 2011-12-24 09:45:55 |
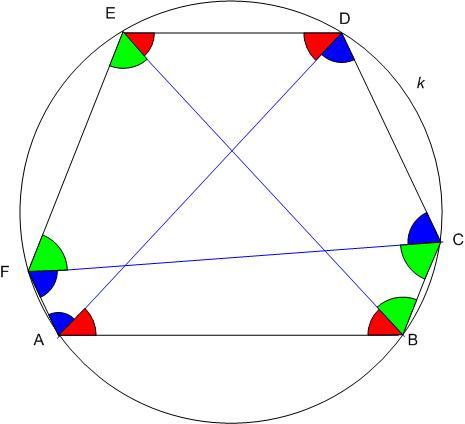
 Elnézést, figyelmetlen voltam. Természetesen nem igaz, hogy az átlók felezik egymást. ( Ld. ábra ) . Egy megoldás: Addig igaz, hogy AB és DE párhuzamosságából valamint AD és BE egyenlő hosszából adódik, hogy a két átló egyenlő szögeket zár be a párhuzamos oldalakkal. Az ábrán pirossal jelölt szögek ABE  = BAD = BAD  = DEB = DEB  = EDA = EDA  , legyen , legyen  . Hasonlóan CDA . Hasonlóan CDA  = FCD = FCD  = DAF = DAF  = CFA = CFA  , legyen , legyen  ( kék ), valamint CBE ( kék ), valamint CBE  = BCF = BCF  = BEF = BEF  = CFE = CFE  , legyen , legyen  ( zöld ). BAD ( zöld ). BAD  = DEB = DEB  miatt ABDE húrnégyszög, körülírt köre legyen k. A hatszög szögeinek összegére 720o = 4 miatt ABDE húrnégyszög, körülírt köre legyen k. A hatszög szögeinek összegére 720o = 4  + 4 + 4  + 4 + 4  , így , így  + +  + +  = 180o . k -ban a BD húrhoz tartozó egyik kerületi szög = 180o . k -ban a BD húrhoz tartozó egyik kerületi szög  , BCD , BCD  = =  + +  , így ABCD húrnégyszög, C is rajta van k -n. Ugyanígy adódik, hogy F is rajta van k -n. , így ABCD húrnégyszög, C is rajta van k -n. Ugyanígy adódik, hogy F is rajta van k -n.
|
 |
| Előzmény: [1526] logarlécész, 2011-12-22 19:00:43 |
|
|
| [1526] logarlécész | 2011-12-22 19:00:43 |
 Szerintem nem feltétlenül felezik egymást a szakaszok (nem a feladat végén, hanem abból, hogy egyenlő hosszúak), én legalábbis nem látom, hogy ez honnan jött.
Viszont azt hiszem, az biztos, hogy ha a hat csúcsból két szemköztit elhagyunk, a maradék húrnégyszöget alkot (egyenlő átlójú trapéz), de ebből következik a megoldás?
|
| Előzmény: [1522] HoA, 2011-12-20 17:31:48 |
|
|
|
|
| [1522] HoA | 2011-12-20 17:31:48 |
 Vázlat: Javaslom a párhuzamos szelők - egyik - tételének egy "megfordítását" : párhuzamosok közötti párhuzamos szakaszok egyenlőek --> párhuzamosok közötti egyenlő szakaszok vagy párhuzamosak vagy ugyanakkora szöget zárnak be a párhuzamosakkal. Ebből adódik, hogy az átlók felezik egymást, és mivel egyenlőek a hat csúcs az átlók metszéspontjától félátlónyi távolságra van, tehát egy körön vannak.
|
| Előzmény: [1521] Erika95, 2011-12-20 17:01:06 |
|
| [1521] Erika95 | 2011-12-20 17:01:06 |
 Sziasztok! A segítségeteket szeretném kérni az alábbi feladat megoldásában: Bizonyítsuk be,hogy egy hatszög szemben fekvő oldalai párhuzamosak és a szembenfekvő csúcsokat összekötő átlók egyenlőek egymással, akkor a hatszög csúcsai egy körön vannak. A hatszög nem biztos hogy szabályos hatszög.
Köszönöm szépen.
|
|
|
|
| [1518] Tatanka Yotanka | 2011-12-12 10:05:37 |
 Kedves Sirpi! Kérdésed, hogy "miért a szögfelezőkre?" teljesen jogos. A DEF háromszög (és a hasonló eljárással létrehozott GHI, JKL háromszögek is) mindig hasonló az ABC háromszöghöz, nem kell, hogy a B,C pontokból az A-ból szögfelezőre bocsássunk merőlegest, elegendő egy A-ból induló, és a szemközti oldalt metsző egyenes, sőt, akár a szemközti oldallal párhuzamos is lehet. A szögfelezős változat nyilván egyszerűbb, a hasonlóság arányát könnyebb fölírni.
|
|
| [1517] Tatanka Yotanka | 2011-12-12 09:09:58 |
 Bocsánat, egy feltételt kihagytam a fölvetett feladatból. Az A pontbeli belső szögfelezőre a B és C pontokból bocsátunk merőlegest. Hiába, kezdő vagyok.
|
|
|
| [1515] Tatanka Yotanka | 2011-12-12 07:00:59 |
 Üdvözlet mindenkinek! Új hozzászólóként szeretnék egy feladatot, illetve problémát fölvetni: Az ABC háromszög A csúcsából bocsássunk merőlegest a szemben levő oldalra, a merőleges talppontja legyen D. Ezután állítsunk merőlegeseket az A-ból induló belső szögfelezőkre, a talppontok itt E és F. Hasonlóképpen szerkesztjük meg a C és B pontokból kiindulva a GHI és JKL háromszögeket. Az könnyen igazolható, hogy DEF, GHI és JKL mindegyike hasonló az ABC háromszöghöz, de ezen háromszögek területének összege lehet-e pl. az ABC háromszög területével egyenlő, annak a fele stb., illetve mennyi a három terület összegének maximuma?
|
|
| [1514] Lajos bácsi | 2011-12-09 18:04:34 |
 Na végre, azt hittem nem lesznek válaszok, de úgy látom, nem sok ember képzelőerejét mozgatta meg a felvetett kérdés.
|
|
|
|
| [1511] Lajos bácsi | 2011-12-07 15:03:45 |
 Rajzoljátok vagy írjátok le azt a 3 dimenziós tárgyat, melyet különbözőképpen elforgatva és megvilágítva az ábrán látható árnyképeket produkálná.
|
 |
|
| [1510] Vonka Vilmos Úr | 2011-06-18 18:18:56 |
 Következzen inkább csak egy kis útmutatás, remélem, utána könnyebb lesz megoldanod a feladatot.
1. Legyen a szabályos n-szög középpontja O, két szomszédos csúcsa A és B. A szabályos n-szög helyett vizsgáljuk az ABO egyenlő szárú háromszöget. Ebben a háromszögben milyen adat R és milyen adat r? Ha ezt meggondoltad, akkor legyen F az AB szakasz felezőpontja, és vizsgáljuk (például) az AFO háromszöget. Ez a háromszög derékszögű (miért?), így bármelyik oldalát könnyedén kiszámíthatjuk szögfüggvények segítségével. Ha már látod, hogy az ABO háromszög milyen adatai R és r, akkor ennek a háromszögnek az oldalhosszai elvezetnek a R-re és r-re vonatkozó formulákhoz.
A terület kiszámításához is elég az ABO háromszög területét meghatároznod. (Hányszorosa ennek a szabályos n-szög területe?)
2. Az előző formulákba n=8-at kell behelyettesíteni. Ehhez pi/8 szögfüggvényeinek pontos értékére van szükséged. Ez egy nevezetes szög (45 fok) fele, ezért a félszögek szögfüggvényeire vonatkozó képletek (nézz utána!) alapján kaphatod meg a szükséges formulákat.
3. Itt szintén az 1. feladatban nyert képletekbe kell behelyettesíteni. A szögfüggvények pontos értékei csak n=5 és n=10 esetén nem annyira ismertek. Ezek közül nyilván elég az egyiket kiszámítani. (A másik a kétszeres szögre vagy félszögre vonatkozó képletek alapján adódik.) n=10 esetén például a 18 fokos szög szögfüggvényeire lesz szükség. Az erre vonatkozó számításokhoz segítség: annak az egyenlő szárú háromszögnek, amelynek alapon nyugvó szögei 72 fokosak, az alapja és a szára az aranymetszés szerint aránylik egymáshoz, azaz arányuk (gyök(5)-1)/2.
|
| Előzmény: [1509] virágzótisza, 2011-06-18 14:50:10 |
|
| [1508] Maga Péter | 2011-06-18 17:28:48 |
 Innen ilyenekért nem fognak kitiltani (feltéve, hogy nem valamely aktív KöMaL-feladathoz kapcsolódik a kérdésed:)), tudunk ,,ilyesmiről'' beszélgetni.
A feladatokat nem lövöm le. Nem tudom, hogy van-e egyáltalán olyan látogatója a fórumnak, aki még életében nem gondolta meg az ismertetett formulákat...
Javaslom az oldalon található TeX tanfolyam elvégzését, már ezeket a bevezető képleteket is kellemetlen ebben a formában olvasni.
|
| Előzmény: [1509] virágzótisza, 2011-06-18 14:50:10 |
|
| [1509] virágzótisza | 2011-06-18 14:50:10 |
 Sziasztok! Ahányszor csak kérdezek, vagy nicket regisztrálok az index fórumon, annyiszor kitörlik kérdésemet és kitiltanak. Most a matematika-elsősegély topikból tiltottak ki az alábbi kérdések miatt.
1. Bizonyítsuk be, hogy az a oldalhosszúságú szabályos n szög köré írt kör sugara R=a/(2sin(pi/n)), beírt kör sugara r=a/2tg(pi/n) terülte S=nar/2 2. Mutassuk meg 1. felhasználásával, hogy a szabályos nyolcszögre R=agyök(1+(gyök2)/2), r=a(1+gyök(2))/2, S=2a**2(1+gyök(2)) 3. Töltse ki az alábbi táblázatot: n, R,r,S, ahol n =3,4,5,6,10 (A fenti alakhoz hasonlóan adja meg a formulákat!)
Tudunk itt ilyesmiről beszélgetni?
|
|
|
|
|
|
|
|
| [1501] gubanc | 2011-04-19 12:03:38 |
 A 2)-höz: Így egyszerűbb volt a számítás, mert meg lehetett spórolni a 4R-es szorzó többszöri leírását.
Köszönöm a részletes "helyretételt". A dorgálást megérdemlem, hiszen egy félreértés miatt árnyékra vetődtem és előbb írtam, mint gondolkoztam. Több tanulság van, az egyik, hogy késő éjszaka, hullafáradtan nem szabad matekoznom ... .
Nem állt szándékomban megbántani, főleg nem Téged, hiszen korábban és most is nagy élvezettel olvastam, olvasom frappáns levezetéseidet, megoldásaidat. Elnézést, ha megbántottalak volna. Üdv: gubanc
|
| Előzmény: [1500] nadorp, 2011-04-19 10:34:47 |
|
| [1500] nadorp | 2011-04-19 10:34:47 |
 Az "álbizonyítás" megjegyzésed kissé erős...De ettől függetlenül:
1). Idézet tőlem: "nálam minden x,y,z távolságra van megoldás ( az más kérdés, hogy ez szerkeszthető-e)"
Ezzel azt a félrértést szeretném eloszlatni, hogy én csak a megoldhatóságot ( diszkussziót ) vizsgáltam, nem a geometriai szerkeszthőséget.
2.) Az eredeti feladat szerint: Szerkesszük meg a háromszöget, ha adottak a beírt kör középpontjának a csúcsoktól mért távolságai.
Nem értem, minek kell feltenni, hogy R=1/4. Adott három független adat, szerkesszük meg a háromszöget ( felejtsd most el a hasonlóságot)
3.) "A (*) tartományon kívül eső szögek nem adnak megoldást."
Ez értelmetlen, mert a (*) tartományba nem szögek, hanem szakaszok hosszai esnek.
4.)"A leírtak következménye: az általad előállított f függvény a t = 0 helyen nincs értelmezve, hiszen  > 0 egyben > 0 egyben  > 0-t is jelenti" > 0-t is jelenti"
Már dehogy nincs értelmezve a t=0 és t=1 helyen, félreértésben vagy. Az, hogy megoldásként csak 0 és 1 közti megoldást fogadunk el, attól még a függvény értelmezve van a végpontokban és a Bolzano-tétel is használható rá. ( Így keletkeznek a "Híres álcáfolatok" ).
Fordítva gondolkozzál, a Bolzano-tétel csak egy eszköz. Az egyenletrendszer megoldásából adódik, hogy ha ennek a függvénynek van (0;1)-beli zéróhelye, akkor az megadja 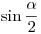 értékét. A Bolzano-tétel ( vagy általában az, hogy zárt intervallumon folytonos függvény tetszőleges két felvett értéke közti értéket is felvesz) csak biztosítja a gyök létezését. A 0 sugarú körrel való "bűvészkedés" helyett pedig tekintsd az f függvényt az [ értékét. A Bolzano-tétel ( vagy általában az, hogy zárt intervallumon folytonos függvény tetszőleges két felvett értéke közti értéket is felvesz) csak biztosítja a gyök létezését. A 0 sugarú körrel való "bűvészkedés" helyett pedig tekintsd az f függvényt az [ ;1- ;1- ] intervallumon, ahol ] intervallumon, ahol  olyan kicsi pozitív szám, hogy f( olyan kicsi pozitív szám, hogy f( )<0 és f(1- )<0 és f(1- )>0 és egyből megszűnnek az értelmezésbel gondjaid. )>0 és egyből megszűnnek az értelmezésbel gondjaid.
5.) "Egyébként jó, hogy ez a probléma is felmerült, mert roppant tanulságosnak tartom"
Akkor tanulj belőle.
|
| Előzmény: [1495] gubanc, 2011-04-19 02:13:48 |
|
| [1499] Kemény Legény | 2011-04-19 10:11:38 |
 "Azt mondod, hogy ha egy racionális együtthatós harmadfokú egyenletnek nincs racionális gyöke, akkor a gyökei nem szerkeszthetőek?"
Igen.
Arra, hogy egy szám nem szerkeszthető, elégséges feltételt ad az, hogy a minimálpolinomjának a foka nem kettőhatvány. Márpedig azok a rac. együtthatós harmadfokú polinomok, amiknek nincs rac. gyökük, irreducibilisek.
|
| Előzmény: [1498] jonas, 2011-04-19 10:02:13 |
|
| [1498] jonas | 2011-04-19 10:02:13 |
 Hogy van ez? Azt mondod, hogy ha egy racionális együtthatós harmadfokú egyenletnek nincs racionális gyöke, akkor a gyökei nem szerkeszthetőek? Ez miért olyan triviális? Negyedfokú egyenletre mondjuk biztos nem lenne igaz, mert mondjuk két általános racionális együtthatós másodfokú polinom szorzata egy olyan racionális együtthatós negyedfokú polinom, aminek nincs racionális gyöke, de minden gyöke szerkeszthető.
|
| Előzmény: [1497] Kemény Legény, 2011-04-19 07:59:51 |
|
| [1497] Kemény Legény | 2011-04-19 07:59:51 |
 Attól most tekintsünk el, hogy mennyire érted/nem érted a Bolzano-tétel használatát (az ember nem szívesen ért egyet Róbert Gidával, de ha egyszer igaza van...), térjünk inkább vissza az euklideszi szerkeszthetőség vizsgálatára. (Mellesleg gyanítom, itt még több olyan rész fog következni, amikkel esetleg gondok lehetnek...)
Állítás: nincs általános módszer, amivel tetszőlegesen adott x,y,z esetén megszerkesztenéd (a szokásos euklideszi szerkesztésekkel) a háromszögedet.
Bizonyítás: A nadorp által levezetett egyenletből kapjuk a harmadfokú 2x2yzt3+(x2y2+y2z2+z2x2)t2-y2z2=0 egyenletet. Ez az egyenlet például az x=1<y=2<z=3 választás esetén a 12t3+49t2-36=0 alakot ölti. A bal oldalon álló egész együtthatós polinomnak nincs racionális gyöke (ha nem ismernéd ennek az eldöntésére szolgáló módszert, kérdezz meg egy Maple, Mathematica, stb. jellegű szoftvert vagy olvasd el itt). Tehát a harmadfokú polinom irreducibilis, a kiindulási adataink: (x,y,z)=(1,2,3) egészek voltak, innen a szerkeszthetőségről szóló Galois-elmélet egyszerű következményeként nem szerkeszthető meg 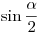 , ami ekvivalens a háromszög szerkesztésének lehetetlenségével. (gondold végig...) , ami ekvivalens a háromszög szerkesztésének lehetetlenségével. (gondold végig...)
|
| Előzmény: [1495] gubanc, 2011-04-19 02:13:48 |
|
| [1496] Róbert Gida | 2011-04-19 02:56:20 |
 nadorp szerintem hallott már a Bolzano tételről... Amúgy miért baj, a nulla sugarú kör? Formálisan miért nem nézhetnéd az egyenletet? [t egy változó] A megoldás (0,1)-beli, azaz nem lesz nulla sugarú kör a megoldás. Ugyanez van a másik oldalon.
Amúgy ezeknek a klasszikus tételeknek vannak javított változatai. Amikor nyílton folytonos és egyoldali limesz van a végpontokban stb.
|
| Előzmény: [1495] gubanc, 2011-04-19 02:13:48 |
|
| [1495] gubanc | 2011-04-19 02:13:48 |
 Szia nadorp!
A folytonos függvényekre vonatkozó Bolzano tételt próbáltad alkalmazni, amely így szól:
Ha a g függvény az [a, b] zárt intervallumon folytonos és g(a), g(b) különböző előjelűek, akkor az intervallumban van olyan c pont, amelyre g(c) = 0.
0 sugarú beírt kör nem értelmezhető, így fennáll, hogy 0 < < x és z < x és z 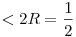 , ahol a háromszög köré írt kör sugara: , ahol a háromszög köré írt kör sugara: 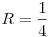 . A távolságokra megadott egyenlőtlenséglánc tehát így teljes: . A távolságokra megadott egyenlőtlenséglánc tehát így teljes: 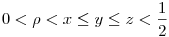 . (*) . (*)
A leírtak következménye: az általad előállított f függvény a t = 0 helyen nincs értelmezve, hiszen  > 0 egyben > 0 egyben  > 0-t is jelenti. A másik végponttal is baj van, hiszen a > 0-t is jelenti. A másik végponttal is baj van, hiszen a 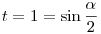 egyenlőségből következne, hogy egyenlőségből következne, hogy  =180°, ami egy háromszöben szintén lehetetlen. Az f függvény tehát nem tesz eleget a Bolzano tétel feltételeinek, így a tétel itt nem alkalmazható. Ezzel megcáfoltuk az állításod, mely szerint „ nálam minden x, y, z távolságra van megoldás”. =180°, ami egy háromszöben szintén lehetetlen. Az f függvény tehát nem tesz eleget a Bolzano tétel feltételeinek, így a tétel itt nem alkalmazható. Ezzel megcáfoltuk az állításod, mely szerint „ nálam minden x, y, z távolságra van megoldás”.
A (*) tartományon kívül eső  szögek nem adnak megoldást. szögek nem adnak megoldást.
(Egyébként jó, hogy ez a probléma is felmerült, mert roppant tanulságosnak tartom. Akár a "Híres(?) álbizonyítások" témába is át lehetne másolni ...)
E kis kitérő után visszatérhetünk az euklidészi szerkeszthetőség vizsgálatára.
|
| Előzmény: [1494] nadorp, 2011-04-17 10:32:14 |
|
| [1494] nadorp | 2011-04-17 10:32:14 |
 Nem tudom, mit számoltam el, de nálam minden x,y,z távolságra van megoldás ( az más kérdés, hogy ez szerkeszthető-e). Vázlatosan:
Tegyük fel, hogy x y y z. Ekkor z. Ekkor
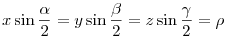 , ahol , ahol  a beírt kör sugara. a beírt kör sugara.
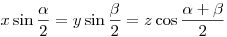

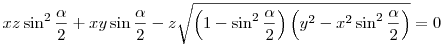
Négyzetre emeléssel és rendezéssel valóban egy harmadfokú egyenletet kapunk 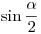 -re, de most nem ez a lényeg, hanem -re, de most nem ez a lényeg, hanem
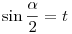 jelöléssel a bal oldalon egy olyan, a [0,1] intervallumon mindenhol értelmezett ( felhasználtuk, hogy y jelöléssel a bal oldalon egy olyan, a [0,1] intervallumon mindenhol értelmezett ( felhasználtuk, hogy y x ), folytonos f(t) függvény áll, amelyre x ), folytonos f(t) függvény áll, amelyre
f(0)=-zy<0 és f(1)=xz+xy>0, tehát létezik zéróhelye a (0,1) intervallumon. Hol a hiba? Nem látom, hogy az így kapott 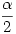 szög mikor nem ad megoldást? szög mikor nem ad megoldást?
|
| Előzmény: [1493] gubanc, 2011-04-16 21:06:36 |
|
| [1493] gubanc | 2011-04-16 21:06:36 |
 Legyenek az 1/4 sugarú körbe írt ABC háromszög szögei  , ,  , ,  . A beírt kör középpontjának az A, B, C csúcsoktól mért távolságai x, y, z. Ezeket kaptam (a részleteket most mellőzöm): . A beírt kör középpontjának az A, B, C csúcsoktól mért távolságai x, y, z. Ezeket kaptam (a részleteket most mellőzöm): 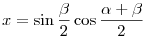 , , 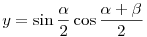 , , 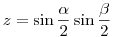 . .
Ezekből kiindulva egyelőre nem tudom kihozni, hogy mely ( , , ) szögpárra szerkeszthető meg az x, y, z távolságokból egy háromszög. Csak a korábban említett halvány "gyanú" merült fel bennem. ) szögpárra szerkeszthető meg az x, y, z távolságokból egy háromszög. Csak a korábban említett halvány "gyanú" merült fel bennem.
A Te harmadfokú egyenleted viszont biztatónak tűnik. Esetleg fel tudnád tenni?
|
| Előzmény: [1492] Maga Péter, 2011-04-14 19:56:58 |
|
| [1492] Maga Péter | 2011-04-14 19:56:58 |
 Én egy harmadfokú egyenletet kaptam. Abból a szerkeszthetőség kérdése (konkrétan megadott kezdeti adatokból) mindig könnyen eldönthető. Az nem világos nekem, hogy a tartományt hogyan lehetne egyszerűen leírni, bár nem is nagyon gondolkodtam rajta. Lehet, hogy nem nehéz, de az is lehet, hogy ennél lényegesen egyszerűbb leírást nem is lehet adni.
|
| Előzmény: [1491] gubanc, 2011-04-14 16:47:40 |
|
| [1491] gubanc | 2011-04-14 16:47:40 |
 Köszönöm, hogy végigszámoltad. Én is ilyen következtetésre jutottam. Ha jól értem, ez azt jelenti, hogy 1-ből hiányzik a szerkeszthető háromszögeket megadó értelmezési tartomány. Ezzel el is jutottunk 2-höz.
|
| Előzmény: [1490] Maga Péter, 2011-04-13 16:24:00 |
|
|
| [1489] gubanc | 2011-04-13 14:41:02 |
 Sziasztok!
Kigondoltam egy feladatot, de nem jövök rá, hogyan kellene hozzáfogni és megoldani. Íme:
1. Szerkesszük meg a háromszöget, ha adottak a beírt kör középpontjának a csúcsoktól mért távolságai.
És/vagy:
2. Melyek azok a háromszögek, amelyek megszerkeszthetők, ha adottak a beírt kör középpontjának a csúcsoktól mért távolságai?
A 2.-nál arra gyanakszom, hogy a keresett háromszögek szögei a nevezetes szögekből származtathatók … (Ha mégsem, vagy nem jók a feladatok, bocsi előre is.)
Köszönettel: gubanc
(Sok van, mi csodálatos, de a Geometriánál nincs semmi csodálatosabb! :)
|
|
|
| [1487] HoA | 2011-04-11 14:41:37 |
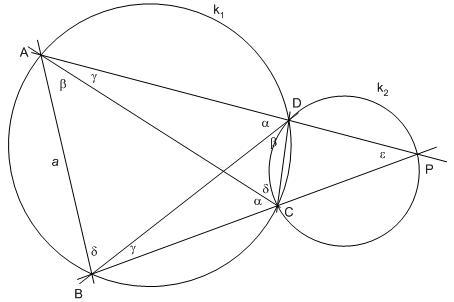
 Komolyra fordítva: Legyen k1 és k2 két egymást metsző kör, metszéspontjaik C és D. k2 kör k1-en kívül eső CD ívén vegyünk fel egy P pontot. A PD és PC egyenesek k1-gyel alkotott második metszéspontja legyen A illetve B . Bizonyítsuk be, hogy az AB=a szakasz hossza független P választásától.
Előkészítésül tekintsünk egy ABCD húrnégyszöget, ahol AB=a>CD=c . A BC és AD egyenesek metszéspontja legyen P . ABCD körülírt körében legyenek az oldalakhoz mint húrokhoz tartozó kerületi szögek  , , , , , , . Ekkor ABCD szögeinek összege 2.( . Ekkor ABCD szögeinek összege 2.( + + + + + + )=360o , tehát )=360o , tehát  + + + + + + =180o . A BPA szöget =180o . A BPA szöget  -nal jelölve az ABP háromszögben -nal jelölve az ABP háromszögben  +2 +2 + + + + =180o= =180o= + + + + + + , ahonnan , ahonnan  = = - -
Feladatunkra alkalmazva az eredményt, a mi ABCD húrnégyszögünkben CD=c rögzített, így  állandó, BPA állandó, BPA = = =CPD =CPD állandó, mint k2-ben a CD húrhoz tartozó kerületi szög, ezért állandó, mint k2-ben a CD húrhoz tartozó kerületi szög, ezért  = = + + is állandó, vagyis k1 -ben az AB húrhoz tartozó kerületi szög és így AB=a hossza is független P helyzetétől. is állandó, vagyis k1 -ben az AB húrhoz tartozó kerületi szög és így AB=a hossza is független P helyzetétől.
|
 |
| Előzmény: [1482] eperke, 2011-04-10 15:38:14 |
|
| [1486] HoA | 2011-04-11 08:17:58 |
 Mi az, ami adott? Például: adott két egymást metsző, egyébként tetszőleges kör ... Ahogy a kérdést feltetted, biztosan nem igaz az állítás: Ha kétszer akkora ábrát rajzolok, az a szakasz is kétszer akkora lesz - akármelyik is legyen az ábrán az a szakasz - mert én azt sem látom, melyik az.
|
| Előzmény: [1482] eperke, 2011-04-10 15:38:14 |
|
| [1485] eperke | 2011-04-10 17:17:34 |
 Ez így jó lesz?Nagyobbra nem megy..:S
|
 |
|
| [1484] jonas | 2011-04-10 16:21:47 |
 A 80-szor 100 pixel méret az avatarra vonatkozik, ami minden hozzászólásod mellett megjelenik. A csatolt ábra lehet nagyobb is, bár az sem lehet túl nagy.
|
| Előzmény: [1482] eperke, 2011-04-10 15:38:14 |
|
| [1483] Radián | 2011-04-10 16:10:05 |
 Hello!
Nem tudnál egy nagyobb képet bevágni, vagy linket küldeni ahol nagyobb méretben, jó felbontásban láthatjuk az ábrát, mert (legalábbis én) így nem tudok segíteni.
|
| Előzmény: [1482] eperke, 2011-04-10 15:38:14 |
|
| [1482] eperke | 2011-04-10 15:38:14 |
 Hali.Egy kis segítségre lenne szükségem. Azt kell belátni , hogy az a szakasz mindig ugyanolyan hosszú.
|
 |
|
| [1481] Füge | 2011-01-19 18:49:05 |
 Jajj elnézést az utolsót visszavonom elnéztem a kettest :)
|
|
| [1480] Füge | 2011-01-19 18:47:45 |
 Ja és igen a megadott képleted is hibás, ugyanis
 tehát tehát 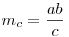
|
|
| [1479] Füge | 2011-01-19 18:36:42 |
 Arra gondoltam, hogy melyik az a legszűkebb intervallum, amelybe mindenképp beleesik az 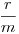 hányados. hányados.
|
|
| [1478] Radián | 2011-01-19 18:23:11 |
 Gyanítom, hogy félreértettem a feladatod de talán a hibás eredményemből majd kiderül mire is gondoltál. Szerintem: r/m=(a+b-c)c/2ab ahol r a beírt kör sugara, m az átfogóhoz tartozó magasság hossza míg a két befogót a ill b-vel az átfogót pedig c-vel jelöltem. Igazából nem értem, hogy ezt miért becsülni kell s nem kiszámolni...
|
| Előzmény: [1477] Füge, 2011-01-19 15:01:45 |
|
| [1477] Füge | 2011-01-19 15:01:45 |
 Egy könnyebb feladat, de nekem tetszett.
174.feladat: Egy tetszőleges derékszögű háromszögben adjuk minél jobb közelítést a beírt kör sugarának és az átfogóhoz tartozó magasságnak a hányadosára.
|
|
| [1476] HoA | 2011-01-07 21:52:17 |
 Ha a P ponton átmenő, sugárra merőleges húr hossza 2a, egy másik húrt a P pont b és c hosszúságú szakaszokra oszt, akkor a szelőtételből
a2=b.c
és a számtani - mértani közép tételből
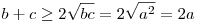
|
| Előzmény: [1465] Nánási József, 2010-12-30 22:47:46 |
|
|
| [1474] BohnerGéza | 2011-01-03 13:45:49 |
 173. feladat: Adott két kör és egy pont. Szerkesztendő az a középpontos hasonlóság, melynek középpontja az adott pont és melynél az egyik kör képe érinti a másik adott kört.
|
|
|
| [1472] Füge | 2011-01-02 14:08:50 |
 Én deriváltam a parabola egyenletét (mert y=ax2+bx+c alakú volt), és azt tettem egyenlővé a kapott meredekséggel, onnan számoltam pontot, majd m(x-x0)=y-y0 A feladat többi részével nem volt gond, csak azon filóztam, hogy kell-e bizonyítás, vagy sem :)
|
|
| [1471] lorantfy | 2011-01-02 13:37:38 |
 Szerintem itt nem kell a bizonyítással vacakolni. Ezt ismertnem vesszük. Felteszem, hogy a P pont az O középpontú körön belül van:
1. Felirjuk P ponton átmenő OP normálvektorú egyenes egyenletét.
2. y-ra rendezzük, hogy meglegyen a meredeksége=m.
3. A parabola érintője y=mx+b alakú, b paraméter.
4. Egyenletrendszer a parabola egyenletével. Behelyettesítve másodfokú egyenlet. Mivel érintőről van szó a diszkrimináns = 0. Ebből megvan b, tehát ismerjül az érintő egyenletét.
5. Felírjuk az OP egyenes egyenletét.
6. OP metszéspontja az érintővel, egyenletrsndszer: Q
7. PQ távolság.
8. Parabola egyenletéből kiolvasni a F pontot
9. Origó F távolsága.
|
| Előzmény: [1466] Füge, 2010-12-30 23:06:03 |
|
| [1470] Füge | 2011-01-02 13:20:29 |
 Igen én is így indultam neki a feladatnak, csak másodfokú egyenlet rendszer, Viéte-formula, deriválás... azért kérdeztem, hátha van szebb megoldás. Abban igazad van, hogy elfelejtettem mondani, hogy a pont a körön belül van, elnézést. Ez egy próbaérettségi feladatsorból az egyik feladat, és gondolom az első két rész kevés volt még ahhoz, hogy 16 pontot adjanak rá, ezért raktak be egy ilyen részfeladatot, hogy ismered-e a koordinátatengelyekkel párhuzamos vezéregyenesű/tengelyű parabola általános egyenletét.
|
|
| [1469] HoA | 2011-01-02 10:34:18 |
 Az origó említéséből arra következtetek, hogy ezt koordináta-geometriai feladatnak szánták. Az alakzatok tehát koordinátáikkal ill. egyenleteikkel adottak. Ekkor az is elképzelhető, a feladatkitűző arra gondolt, a P ponton átmenő legrövidebb húr meghatározásához írjuk fel a P-n áthaladó általános egyenes egyenletét m iránytangensével paraméterezve, számítsuk ki a körrel alkotott metszéspontok koordinátáit és keressük meg, e két pont távolsága melyik m-re lesz a legkisebb. ( Azt talán illett volna közölni, hogy P a körön belüli pont. )
Amit nem értek: hogy jön a harmadik kérdés az első kettőhöz? Ha adott a parabola, akkor fókusza, és így annak origótól mért távolsága is "adott" ( kiszámítható), függetlenül attól, hogy veszek-e fel egyáltalán még kört meg pontot a síkban. Ettől persze a feladat még korrekt.
|
| Előzmény: [1466] Füge, 2010-12-30 23:06:03 |
|
| [1468] Füge | 2010-12-30 23:11:42 |
 Érettségin kétlem, hogy megkérnek majd, úgyhogy marad az említés :)
|
|
| [1467] Nánási József | 2010-12-30 23:09:20 |
 Ez a Geometria 1-ben vagy 2-ben is benne van... //nekem is aktuális feladat volt nem rég
Nálunk kellett említés szerűen mondani, hogy az a legrövidebb, csak aztán meglettem kérve, hogy bizonyítsam be a táblánál.
|
|
| [1466] Füge | 2010-12-30 23:06:03 |
 Köszönöm a gyors választ. A feladat az volt, hogy adott egy parabola egy kör és egy pont. A parabola azon érintőjét keressük ami párhuzamos a P ponton átmenő legrövidebb húrral(6 pont), milyen messze van a P ponttól(5 pont) és mekkora a parabola fókuszpontjának távolsága az origótól(5 pont). Elképzelhető, hogy kell ez a bizonyítás a feladathoz, vagy elég lehet annyi, hogy triviális? Esetleg, egy egy mondatos indoklás?
|
|
| [1465] Nánási József | 2010-12-30 22:47:46 |
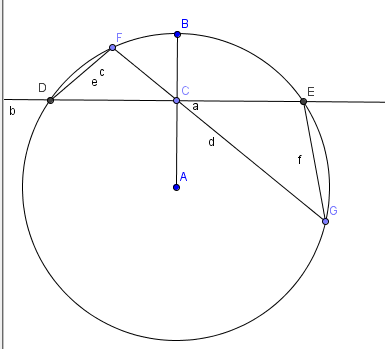
 Legyen ACD szög derékszög, ekkor DC és CE egyenlő (DE húrja a körnek)(mostantól x jelölöm)
Legyen CF y, míg CG z-vel jelölve.
DCF szög és ECG szög egyenlő, mert csúcsszögek.
DFG és DEG szögek egyenlőek, mivel azonos ívhez tartozó kerületi szögek, azaz DFC és CEG minden szöge megegyezik, így hasonlóak.
Hasonlóság miatt:
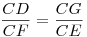
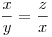
Mivel ezek valós szakaszok, emiatt az egyenletet átrendezve:
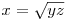
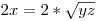
Tegyük fel hogy y+z kisebb mint 2x.
2x helyére írjuk be y+z-t, illetve az egyenletnek vegyük a kettővel képzett hányadosát. Ekkor azt várjuk, hogy hogy az egyenlet bal oldala kisebb lesz mint a jobb.
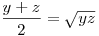
A számtani mértani közép tulajdonsága miatt, az egyenlet bal oldala nagyobb mint ajobb (S>M)
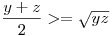
Itt tehát ellentmondás áll fent, azaz y+z>=2x.
Az egyenlet akkor és csak akkor teljesül, ha y=z, amikor pedig a merőleges húrt kapjuk vissza.
Tehát a legrövidebb húr a sugárra merőleges.
|
 |
|
| [1464] Füge | 2010-12-30 22:09:02 |
 Üdv!
Egy eléggé elemi kérdésem lenne, amire nem tudtam választ keríteni. Adott körben adott ponton átmenő húrok közül melyik a legrövidebb? Illetve az triviális, hogy a húrra merőleges, de bizonyítani nem nagyon tudtam.
(Megjegyzés: Próbaérettségi feladat emelt szint, II. rész, a feladat a,b,c, részből áll, és ezt az a, rész felénél kellene használni, szóval nem lenne rossz valami rövidebb bizonyítás)
|
|
| [1463] BohnerGéza | 2010-11-17 11:29:48 |
 Másik megoldást kaphatunk, ha észrevesszük az A*B1B2 és A*C1C2 háromszögek hasonlóságát. Területet is fölhasználva megadhatjuk, hogy AA* metszéspontja milyen osztóviszonyt ad BC-n. ...
|
| Előzmény: [1462] BohnerGéza, 2010-11-17 11:23:56 |
|
| [1462] BohnerGéza | 2010-11-17 11:23:56 |
 Az idei Kürschák-verseny 2. feladata: Az ABC háromszög AB oldalának belsejében adottak a C1 és C2 pontok, a BC oldal belsejében az A1 és A2 pontok, végül a CA oldal belsejében a B1 és B2 pontok úgy, hogy AC1<AC2, BA1<BA2, és CB1<CB2 teljesül.
Az AB1C1 és AB2C2 körök A-tól különböző metszéspontját jelölje A*, a BC1A1 és BC2A2 körök B-től különböző metszéspontja legyen B*, végül a CA1B1 és CA2B2 körök C-től különböző metszéspontját nevezzük C*-nak.
Mutassuk meg, hogy az AA*, BB* és CC* egyenesek egy ponton mennek át!
|
 |
|
| [1461] Tóbi | 2010-10-27 16:15:30 |
 Kiszámolni nem nehéz, bár azt nem látom miért igaz. Feltehető, hogy a henger tengelye a z tengely, sugara r, míg a paraboloidot az xy síktól és a P=(a,0,b) ponttól egyenlő távol lévő pontok alkotják. Ekkor ha (x,y,z) mindkét alakzatnak eleme:
x2+y2=r2
(x-a)2+y2+(b-z)2=z2
Kivonva a két sort egymásból:
2ax+2bz=a2+b2+r2
Tehát a metszet benne van a fenti síkban.
|
| Előzmény: [1460] HoA, 2010-10-27 10:56:11 |
|
| [1460] HoA | 2010-10-27 10:56:11 |
 Rég nem volt feladat. Az alábbiról sem állítom, hogy új ( RóbertGida biztos tud forrást is hozzá ) , nekem is egy korábbi KöMaL feladat kapcsán jutott eszembe:
Bizonyítsuk be, hogy egymással párhuzamos tengelyű forgási paraboloid és végtelen körhenger metszésvonala síkgörbe.
|
|
| [1459] Lóczi Lajos | 2010-10-03 22:54:39 |
 Képlet, zárt alak, stb. akkor lesz az inverzre, ha valaki bevezet erre vagy az ehhez hasonló függvényre egy új nevet és kiszámolja néhány tulajdonságát.
Az elmúlt évszázadokban ez sok tucatszor megtörtént a fontosnak bizonyult függvények esetén, amelyek nem voltak "elemi függvények". Így született meg a "speciális függvények" azóta is egyre bővülő osztálya. Rögtön világossá válik a helyzet, ha vetsz egy pillantást egy ilyen gyűjteményre, pl. itt. Ezen függvények mindegyikét hívhatod "zárt alaknak". A hozzászólásodban említett függvény inverze is zárt alakú lesz, ha elnevezed pl. ojozso(x)-nek.
|
| Előzmény: [1458] ojozso, 2010-10-03 20:17:28 |
|
| [1458] ojozso | 2010-10-03 20:17:28 |
 Köszönöm mindenkinek a segítséget a 172. feldattal kapcsolatban, egyik szemem sír (nincs elemi megoldás), a másik nevet (nem a tudásom kopott meg 30 évvel az érettségi után...). A feladatot nem én, hanem az "Élet" alkotta: egy hangszerkesztő programban a megrajzolt körív szerint kellene a dinamikát (ennek révén az átlagos hangosságot) változtatni. A változtatás mértéke nyilván valamilyen arányosságban áll a körszelet területével: minél "domborúbb" (kisebb sugarú a körív), annál nagyobb lesz az átlagos hangosság-növelés (és dinamika-csökkentés). Az elérni kívánt és az aktuális hangosság-szint hányadosa adott, ennek megfelelően adott a körszelet területe is; ebből kellene a körív sugarát meghatározni, majd ha ez megvan, a körív tetszőleges pontjának koordinátáit meghatározni (ami viszont már könnyű). Abban egyetérthetünk, hogy PONTOSAN az adott körszelet területét egy, és csakis egy bizonyos sugarú körív biztosítja: a terület és a sugár között szigorúan monoton megfeleltetés van: minél nagyobb a sugár, annál kisebb a terület. Határértékkel: ha a sugár tart végtelenhez, a terület tart 0-hoz. Képlet hiányában a sugarat próbálkozásokkal be fogom tudni "lőni" tetszőleges pontossággal a területhez (végülis számítógépes program fogja számolgatni), csak elegánsabbnak gondoltam a képlet alkalmazását, ezért tettem fel a feladatot.
A matematikához visszatérve, úgy gondolom, előbb-utóbb lesz zárt alak az általam felvetett és az ahhoz hasonló (pl. a későbbiekben említett) függvény INVERZÉRE is, de az NEM elemi módszerekkel lesz levezetve!
|
|
| [1457] Lóczi Lajos | 2010-10-03 15:28:45 |
 Ahogyan már el is hangzott, ezek olyan elemi függvények, amelyeknek az inverze nem elemi függvény. Persze a függvény is és az inverze is hatványsorba fejthető például, amiből közelítő megoldásokat ki lehet olvasni.
|
| Előzmény: [1455] HoA, 2010-10-01 23:02:52 |
|
| [1456] jonas | 2010-10-02 17:18:57 |
 Az én kedvenc példám az efféle egyenletekre az, amikor egy ellipszispályán keringő bolygó helyét akarjuk megadni az idő függvényében. Ez általában egy sinx=ax+b típusú egyenletre vezet, aminek elemi függvényekkel nem lehet megtalálni a megoldását. A helyből az időt viszont vissza lehet számolni csak elemi függvényekkel.
|
|
| [1455] HoA | 2010-10-01 23:02:52 |
 Kedves matematikus fórum látogatók! Igen, azt hiszem itt az a kérdés, van-e valamilyen fogalom az ilyen értelemben nem invertálhazó függvényekre. Vagyis amikor y kifejezhető zárt alakban x függvényeként, például
y=x+sin(x)
, de x nem adható meg zárt alakban y függvényeként.
|
| Előzmény: [1454] Gubbubu, 2010-10-01 22:05:05 |
|
| [1454] Gubbubu | 2010-10-01 22:05:05 |
 Nem is az a fő baj, hogy transzcendens (tkp. az abszolútértékes egyenletek is transzcendensek, mégis szépen meg lehet őket oldani :-). Talán érdemes lenne a Wikipédiában megnézni az implicitfüggvény-tétel c. szócikket, az én ismerettáramban ez a legközelebbi fogalom, aminek egyáltalán köze lehet a feladatodhoz, bár hogy alkalmazható-e ... ? Amúgy a probléma maga szép, amit feladtál. :-)
|
| Előzmény: [1453] nadorp, 2010-10-01 12:15:55 |
|
| [1453] nadorp | 2010-10-01 12:15:55 |
 A végeredményed jó, de ebből r-t szerintem nem lehet kifejezni, mert ez egy transzcendens egyenlet. ( hasonlóan pld. az x=3sinx egyenlethez). Csak közelítő megoldás van.
|
| Előzmény: [1452] ojozso, 2010-09-29 20:20:00 |
|
| [1452] ojozso | 2010-09-29 20:20:00 |
 Köszi a választ!
Én is próbálkoztam a megoldással, mielőtt feltettem a Fórumra a feladatot, csak nem akartam befolyásolni vele senkit.
Most leírom, meddig jutottam el.
A körszelet területe (t): Tkorszelet=Tkorcikk-TQOCharomszog.
A HÁROMSZÖG TERÜLETE:
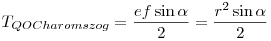 , mivel e=f=r , mivel e=f=r
OFQ derékszögű háromszögben (F az OC szakasz felezőpontja) OQF szög  fele. Szinusz definíciója alapján: fele. Szinusz definíciója alapján:
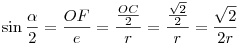 , mivel , mivel 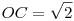 (OC szakasz egységnyi befogókkal rendelkező háromszög átfogója). (OC szakasz egységnyi befogókkal rendelkező háromszög átfogója).
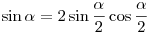 . (Kétszeres szög szinusza). A . (Kétszeres szög szinusza). A 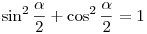 azonosságból: azonosságból: 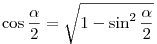 , melyet behelyettesítve kapjuk: , melyet behelyettesítve kapjuk:
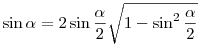 . Beírva . Beírva 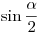 -re kapott -re kapott 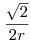 értéket: értéket:
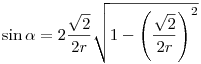 . Egyszerűbb alakra hozva megkapjuk, hogy . Egyszerűbb alakra hozva megkapjuk, hogy 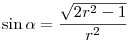
A háromszög területe tehát:
| (1) | 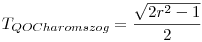 |
A KÖRCIKK TERÜLETE:
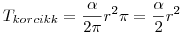 ( ( radiánban.), vagyis: radiánban.), vagyis:
| (2) | 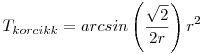 |
A KÖRSZELET TERÜLETE:
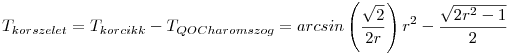
És itt a végállomás! Fogalmam sincs, hogyan lehetne ebből r-et kifejezni, már csak azért sem, mert r az arcsin argumentumában is szerepel és nem tudom, hogyan lehet onnan kihozni.
Innentől kéne segítség. Ráadásul abban sem vagyok biztos, hogy eredményem ekvivalens-e a Tieddel.
|
 |
| Előzmény: [1450] Gubbubu, 2010-09-28 12:19:53 |
|
|
| [1450] Gubbubu | 2010-09-28 12:19:53 |
 Az első feladatra nekem az 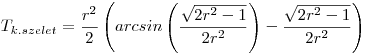
A megoldás leírásához szükséges időm most túl kevés, estefelé vagy pár nap múlva talán; így a képzeletbeli margón marad :-).
Szükséges lenne természetesen az ért. tartományok vizsgálata is, továbbá esetleges geometriai diszkusszió. Nagy vonalakban az történt, hogy kiszámolod a körcikk területét (ez egyszerű egyenes arányosság), majd az ún. trigonometrikus területképlettel az OAC háromszögét, és kivonod a kettőt egymásból. Ezután kifejezed az omega szöget az r segítségével (ehhez ügyeskedni kell az addíciós tételekkel), így eltüntetvén az omegát a képletből (opcionális, az arcsin-elt kifejezés egyébként maga a szinusz omega).
|
| Előzmény: [1449] ojozso, 2010-09-27 18:49:48 |
|
| [1449] ojozso | 2010-09-27 18:49:48 |
 Sziasztok!
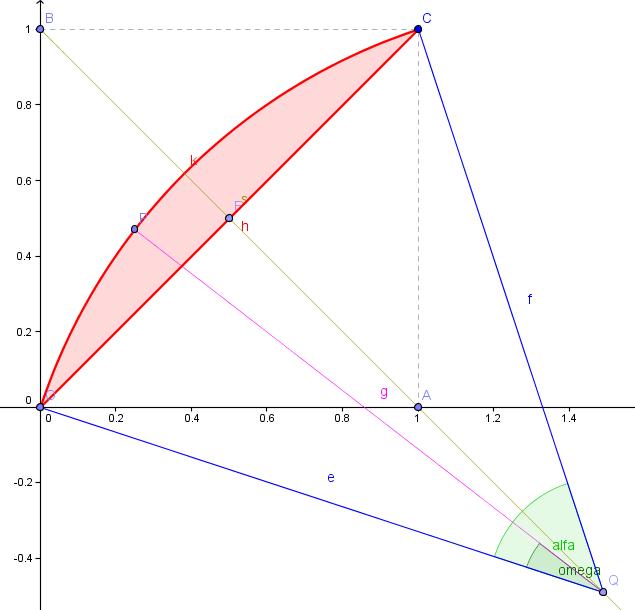
Új vagyok itt és adódott egy probléma, melyen nem tudok túljutni, de Nektek bizonyára menni fog... Tehát:
172. feladat
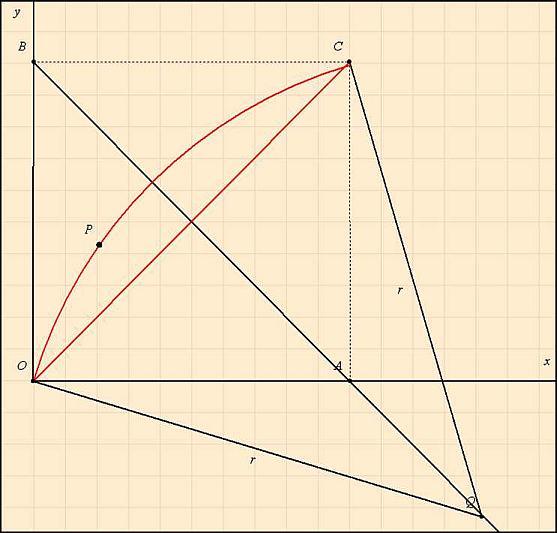
Jelöljük O-val az origót (0;0), A-val az (1;0), B-vel a (0;1) és C-vel az (1;1) pontokat. Az AB szakasz A ponton túli meghosszabításával kapott félegyenesen AB szakaszon kívül vegyünk fel egy tetszőleges Q (u;v) pontot. QO=QC=r sugárral rajzoljuk fel a Q középpontú OC körívet. Ezen a köríven vegyünk fel egy tetszőleges P (x;y) pontot. Az OC szakasz és az OC körív által (pirossal) határolt körszelet területét jelöljük t-vel, az OQP szöget pedig omega-val (QP szakasz sajnos, lemaradt a rajzról.)
Határozzuk meg az adott t területű körszelethez tartozó r sugarat!
Írjuk fel az adott adott t területű körszelethez tartozó körív tetszőleges P pontjának koordinátáit r és omega függvényében!
|
 |
|
|
