| [936] Bubóka | 2007-11-16 06:59:56 |
 Egyetemi jegyzetben található, a szerkesztő általi sajátos jelölési mód (szerintem)A jobb oldalon az "a" oldal a magasság, illetve a szögfelező adatai vannak. A p- pí akar lenni, így (el lett írva) nem a oldal hanem alfa szög.
|
| Előzmény: [935] HoA, 2007-11-15 14:19:10 |
|
| [935] HoA | 2007-11-15 14:19:10 |
 Én sem tudom, mennyire egyezményesek, pedig nem akarom ide írni hány éve foglalkozom szerkesztési feladatokkal. Honnan vetted ezt a jelölést és mit jelent? A baloldalakat majdnem megmagyaráztad - ha jól sejtem az a oldal, az ma magasság és a fb szögfelező adott. De mit jelentenek a jobboldalak?
|
| Előzmény: [934] Bubóka, 2007-11-11 19:58:01 |
|
| [934] Bubóka | 2007-11-11 19:58:01 |
 Üdv Mindenkinek!
Segítséget szeretnék kérni a következő feladathoz.Nagyon fontos lenne!
Bizonyítsuk be, hogy az alábbi háromszögszerkesztési feladatok nem szerkeszthetők euklidészi értelemben! A harmadfokú problémáknál vizsgáljuk, hogy megoldható-e szögharmadoló eszközzel.
1. (a, ha, wb ) = ( p/2, 1, 2 )
2. (a, ha, wb ) = ( 1, 1, 1 )
Nem tudom mennyire egyezményesek ezek a jelek, a w - a szögfelezőt, h- a magasságot jelentené.
|
|
| [933] sakkmath | 2007-11-07 17:51:31 |
 Megoldásra ajánlom a következő feladatot.
Az R pont a K középpontú kör PQ húrjának felezéspontja. Bizonyítsuk be, hogy az ábra szerinti elrendezésben SY>RX. Elnézést, a rajz most csak ilyenre sikeredett :(
|
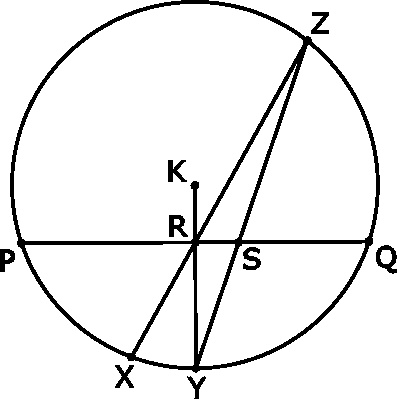 |
|
|
| [931] Fálesz Mihály | 2007-11-05 13:48:22 |
 Egyáltalán nem fitymálni akartam a mátrixos megközelítést. A gyakorlatban is mátrixokat használnak (pl. a számítógépes grafikában).
* * *
Nézzük meg inkább a kvaterniós megoldást.
Legyen u egy egységvektor,  egy szög és egy szög és
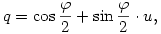
tehát q az a kvaternió, aminek skalár része 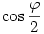 , vektor része pedig , vektor része pedig 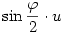 . Nézzük meg, mit csinál a következő leképezés: . Nézzük meg, mit csinál a következő leképezés:
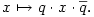
Az x kvaterniót felírhatjuk a+bu+v alakban, ahol a,b skalárok, v pedig egy u-ra merőleges vektor. Legyen w=u×v a v elforgatottja u körül derékszöggel; némi számolás után kijön, hogy
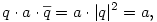
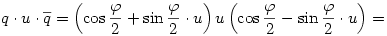
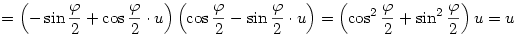
és
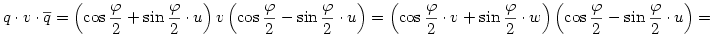
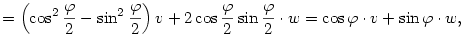
tehát
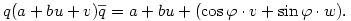
A skalár rész és az u-val párhuzamos vektor komponens nem változik, az u-ra merőleges vektor komponens pedig elfordul  szöggel. Vagyis a művelet elforgatja a vektor részt u körül szöggel. Vagyis a művelet elforgatja a vektor részt u körül  szöggel. szöggel.
|
| Előzmény: [928] BohnerGéza, 2007-11-05 01:57:56 |
|
|
|
| [928] BohnerGéza | 2007-11-05 01:57:56 |
 Beismerem, a kvaterniókkal nem foglalkoztam, csak a síkbeliekkel, azaz a komplex számokkal. (remélem nem tévedek)
Az előző hozzászólásomban leírtak a komplex számok segítségével történő forgatásnál is kellenek (eltolás - forgatás - visszatolás) kivonás - szorzás - visszaadás alakban. Talán szebb, de a számítógép számára ugyanannyi lépés.
A sik összes egyenes és osztóviszony tartó leképezése megadható olyan speciális mátrixszal, melynek utolsó sora 0,0,1, (utolsó oszlopa pedig az origó képe és az 1-es.) azaz hat paramétert kell meghatározni. Az (x;y) képét a mátrixot az (x;y;1) oszlopvektorral szorozva kapjuk. Ez 4 szorzást és 6 összeadást jelent. (Térben 9 szorzás és 12 összeadás.)
|
| Előzmény: [927] Fálesz Mihály, 2007-11-04 23:07:02 |
|
|
| [926] BohnerGéza | 2007-11-04 22:46:22 |
 Az O-t helybenhagyó leképezések egyszerűbbek, ezért ilyen az általános módszer.
Egy-egy speciális eset lehet egyszerűbb, de mindenképpen ajánlom az általánossal való foglalkozást.
|
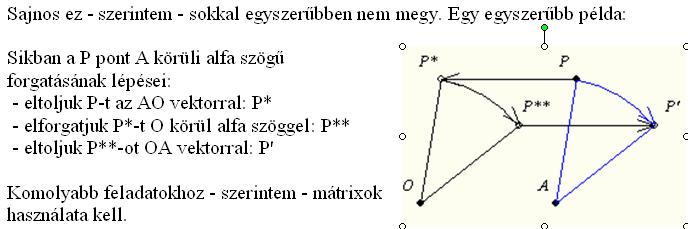 |
| Előzmény: [925] farkasb, 2007-11-04 21:31:19 |
|
| [925] farkasb | 2007-11-04 21:31:19 |
 Lehet, hogy félreértettük egymást, vagy csak számomra tűnik túl bonyolultnak a megoldás, ezért a félreértés elkerülése végett feltöltök egy ábrát. Lényegében a Keresett B' pont rajta van a síkon, és az AB köríven, és mondjuk AB szakasztól 55 fokkal van elforgatva.
|
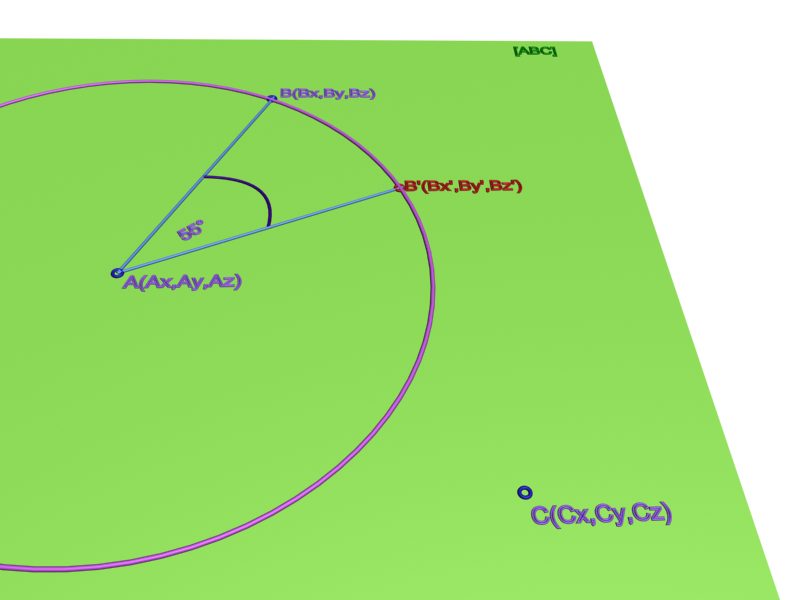 |
| Előzmény: [923] BohnerGéza, 2007-11-02 04:49:24 |
|
| [924] Bubóka | 2007-11-02 13:02:27 |
 Tisztelt Fórumozók!
Segítségeteket kérném! A napokban hallottam a geogebráról. Valaki küldjön már nekem legyen szíves egy feladatot (ami esetleg egy nyomvonalat is tartalmaz) és annak megoldását, amit a geogebrával készített el.
Köszi!
|
|
|
| [922] farkasb | 2007-11-01 10:52:36 |
 Kedves Fórumozók!
Ismételten segítségre szorulok. Adott ABC pont xyz koordinátákkal, ami meghatároz egy síkot. A pont körül hogyan tudom a síkban elforgatni B-t egy tetszőleges szöggel?
|
|
|
|
| [919] Cckek | 2007-10-25 23:02:49 |
 Köszönöm mindkettőtöknek, HoA és Bohner Géza ezeket az érdekes hozzászolásokat, nekem is van egy "csúnya" trigonometrikus megoldásom, de ez nem vetekszik egyikötök megoldásával sem. Köszi.
|
|
| [918] farkasb | 2007-10-25 22:59:45 |
 Kedves Fórumozók!
Lenne egy újabb kérdésem/problémám.
Térbeli koordináta transzformációl lenne szó.
Adott két derékszögű koordináta rendszer, és egy P pont.
Az eredeti koordináta rendszer origója (0,0,0)
X tengelyén A (29.955,2,556,-39,952) //50 egységre O-tól
Y tengelyén B (10.063,47,815,10,604) //50 egységre O-tól
Z tengelyén C (38.748,-14.393,28.132) //50 egységre O-tól
P(20.653,53.039,4,877)
A cél koordináta rendszer origója szintén (0,0,0)
X tengelyén A' (50,0,0)
Y tengelyén B' (0,50,0)
Z tengelyén C' (0,0,50)
Keresett a P pont cél koordináta rendszer beli x,y,z koordinátája.
3dStudio Max porgrammal csináltam meg fordítva az egészet, és a keresett P' pont koordinátái: (10,30,15)
Próbáltam kiszámolni ezt a forgatást, de sehogy sem jött össze. Ezért kérnék némi segítséget.
Ezeket a képleteket használtam:
r11= cos(gamma)*cos(béta)
r12= cos(gamma)*sin(béta)*sin(alfa)-sin(gamma)*cos(alfa)
r13= cos(gamma)*sin(béta)*cos(alfa)+sin(gamma)*sin(alfa)
r21= sin(gamma)*cos(béta)
r22= sin(gamma)*sin(béta)*sin(alfa)+cos(gamma)*cos(alfa)
r23= sin(gamma)*sin(gamma)*sin(béta)*cos(alfa)-cos(gamma)*sin(alfa)
r31= -sin(béta)
r32= cos(béta)*sin(alfa)
r33= cos(béta)*cos(alfa)
P'x= r11* Px+ r12* Py+ r13* Pz
P'y= r21* Px+ r22* Py+ r23* Pz
P'z= r31* Px+ r32* Py+ r33* Pz
Előre is köszönöm a segítséget!
|
|
| [917] HoA | 2007-10-25 19:19:39 |
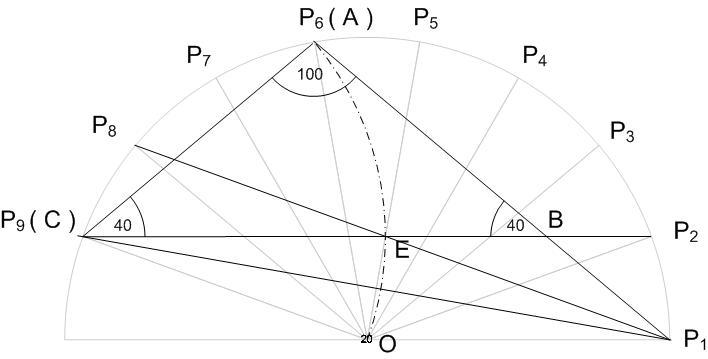
 A KöMaL régebbi olvasói számára ismert, hogy az ilyen feladatok megoldásához, ahol a  -ek szögei 10o egész számú többszörösei, jól használható a szabályos 18-szög oldalaiból, átlóiból és körülírt K köréből álló H18 hálózat. Ha ívhossz egységnek K két szomszédos csúcs közötti ívét vesszük, n egységnyi ívhez n.10o kerületi és n.20o középponti szög tartozik. -ek szögei 10o egész számú többszörösei, jól használható a szabályos 18-szög oldalaiból, átlóiból és körülírt K köréből álló H18 hálózat. Ha ívhossz egységnek K két szomszédos csúcs közötti ívét vesszük, n egységnyi ívhez n.10o kerületi és n.20o középponti szög tartozik.
Legyenek H18 csúcsai P1,.., P18, K középpontja O, sugara R. Húzzuk be a P1P6, P2P9 és P6P9 átlókat. Legyen A=P6,C=P9 , B pedig P1P6 és P2P9 metszéspontja. Ekkor ABC a feladatban szereplő  , hiszen P1P6P9 , hiszen P1P6P9 =100o és P2P9P6 =100o és P2P9P6 =40o. =40o.
OP6P9 R oldalú szabályos  . Legyen a C középpontú R sugarú kör és a BC szakasz metszéspontja E. Ekkor BE a feladatban szereplő oldalhossz különbség. OCE egyenlőszárú . Legyen a C középpontú R sugarú kör és a BC szakasz metszéspontja E. Ekkor BE a feladatban szereplő oldalhossz különbség. OCE egyenlőszárú  csúcsszöge 60o-40o=20o, COE csúcsszöge 60o-40o=20o, COE =80o , E rajta van az OP5 sugáron. De akkor E a P2P9 átló e sugárra vett tükörképén, P1P8 -on is rajta van. A BP1E =80o , E rajta van az OP5 sugáron. De akkor E a P2P9 átló e sugárra vett tükörképén, P1P8 -on is rajta van. A BP1E -ben BP1E -ben BP1E =P6P1P8 =P6P1P8 =20o, a B-nél lévő külső szög 40o, P1BE =20o, a B-nél lévő külső szög 40o, P1BE egyenlőszárú, így P1 feladatunk D pontja. ADC egyenlőszárú, így P1 feladatunk D pontja. ADC =P6P1P9 =P6P1P9 =30o. =30o.
|
 |
| Előzmény: [910] Cckek, 2007-10-21 07:31:36 |
|
|
|
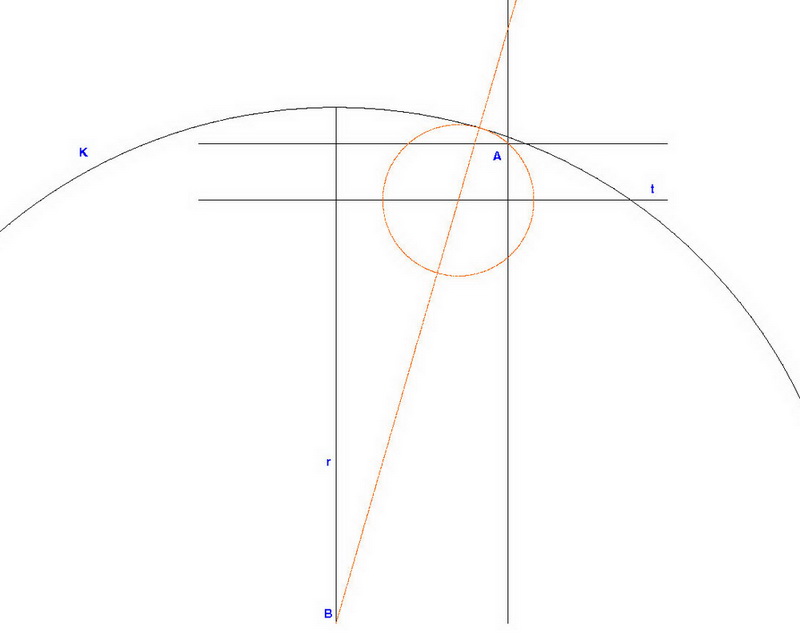
| [914] Draskóczy Gergely | 2007-10-24 16:30:12 |
 Munkám során merült föl az alábbi probléma:
adott A pont, K kör, t egyenes
szerkesszünk geometriai úton olyan kört (2 is van) mely átmegy A ponton, középpontja t egyenesen van, érinti a K kört
Tud ebben valaki segíteni?
Gergő
|
 |
|
|
|
|
|
| [910] Cckek | 2007-10-21 07:31:36 |
 Az ABC háromszögben mA=100o,mB=40o,mC=40o. Az AB oldalt meghosszabbítjuk BD=BC-AB-vel. Határozzuk meg az ADC szög mértékét.
|
|
| [909] farkasb | 2007-10-16 21:09:35 |
 Ezt a hozzászólást és levezetést is köszönöm!
|
|
|
|
|
|
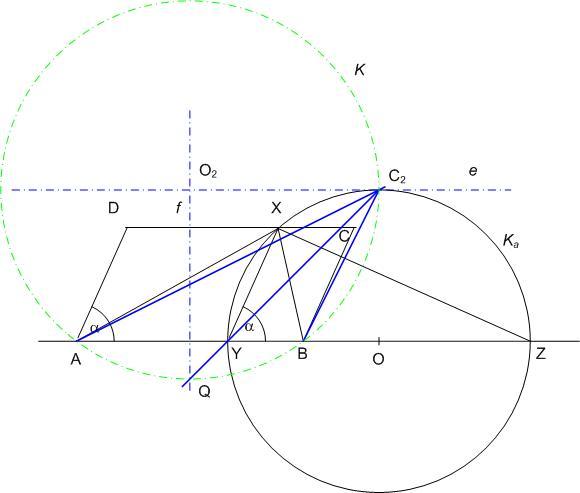
| [904] HoA | 2007-10-16 16:34:08 |
 Legyen adott a paralellogramma az a, b,  adatokkal. A szerkesztendő X ill. Y pontok [885] szerint. A Ka Apolloniusz-kör átmérője d=b/cos adatokkal. A szerkesztendő X ill. Y pontok [885] szerint. A Ka Apolloniusz-kör átmérője d=b/cos és ra=d/2 sugara szintén adottnak tekinthető. Érintse az AB-vel párhuzamos e egyenes Ka-t C2-ben. Ka minden pontjára, így C2-re is igaz, hogy az AC2B és ra=d/2 sugara szintén adottnak tekinthető. Érintse az AB-vel párhuzamos e egyenes Ka-t C2-ben. Ka minden pontjára, így C2-re is igaz, hogy az AC2B felezője AB-t Y-ban metszi. Legyen ABC2 felezője AB-t Y-ban metszi. Legyen ABC2 körülírt K körének sugara R, középpontja O2. Tudjuk, hogy a belső szögfelező a szemközti oldal felező merőlegesét a körülírt körön metszi. Legyen C2Y és K metszéspontja Q. QC2O2 körülírt K körének sugara R, középpontja O2. Tudjuk, hogy a belső szögfelező a szemközti oldal felező merőlegesét a körülírt körön metszi. Legyen C2Y és K metszéspontja Q. QC2O2 egyenlőszárú, mert C2O2=QO2=R. C2QO2 egyenlőszárú, mert C2O2=QO2=R. C2QO2 =OC2Y =OC2Y =45 fok, tehát QO2C2 =45 fok, tehát QO2C2 =90 fok, ami azt jelenti, hogy O2 e-n van. =90 fok, ami azt jelenti, hogy O2 e-n van.
Innen az alábbi szerkesztés adódik: Az a hosszúságú AB szakasszal párhuzamosan, tőle ra távolságra vegyük fel az e egyenest. AB f felező merőlegesének és e-nek a metszéspontja O2. Az O2 középpontú, R=O2A sugarú K kör és e (egyik) metszéspontja C2, K és f metszéspontja ( e egyenes AB-t tartalmazó oldalán ) Q. C2Q kimetszi AB-ből Y-t.
|
 |
| Előzmény: [890] HoA, 2007-10-11 18:08:18 |
|
|
| [902] farkasb | 2007-10-16 15:13:47 |
 Megpróbálom magyarul :)
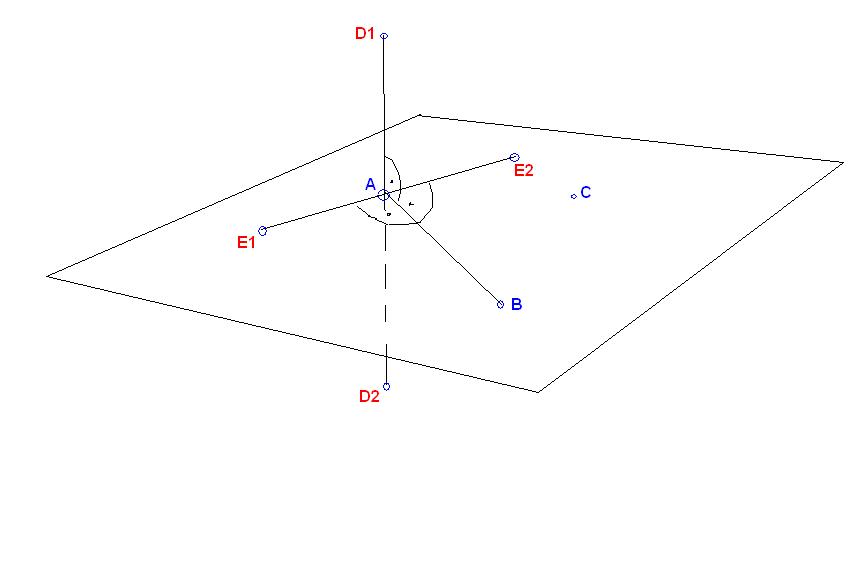
Adott ABC pont xyz koordinátákkal. Keresett 4 db pont. -Az első kettő (D1, D2), amelyik az BA szakaszra merőleges, B-től mért távolsága +10, -10 egység, és a BD1, BD2 merőleges az ABC síkra. A másik kettő (E1, E2)pedig ugyancsak merőleges a BA szakaszra, de az ABC síkon van, és B-től mért távolsága 10 e. Itt egy szemléltető ábra is. Előre is köszönet!
|
 |
|
| [901] HoA | 2007-10-16 14:19:52 |
 Első kérdés : (ld. BohnerGézáé) Az ABC síkra merőleges vetítésre gondolsz?
Második kérdés: AZ ABC síkban fekvő, B-nél derékszögű ABC*  C* csúcsát keresed, ahol BC* = 10 egység? C* csúcsát keresed, ahol BC* = 10 egység?
|
| Előzmény: [899] farkasb, 2007-10-16 12:06:35 |
|
| [900] BohnerGéza | 2007-10-16 14:12:04 |
 Nem érthető (számomra) a feladat! Azt a részt, hogy egy pont legyen merőleges egy szakaszra, azt valószínűleg más sem érti.
Az elején merőleges vetítés van?
Fogalmazd meg jól a feladatot, talán tudunk segíteni.
|
| Előzmény: [899] farkasb, 2007-10-16 12:06:35 |
|
| [899] farkasb | 2007-10-16 12:06:35 |
 Kedves Fórumozók!
Ilyen nehezet kérdeztem (nem hinném), vagy túl egyszerű? Megköszönném, ha valaki tudna segíteni.
|
|
| [898] farkasb | 2007-10-14 23:16:22 |
 Egy újabb, elvileg egyszerű kérdésem lenne. Adott A B C pont a térben. -Hogyan határozhatom meg azt a pontot(pontokat), mely az ABC síkra vetítve a vetítősugár a B ponton menne át, és B ponttól 10 egységnyire van. -továbbá szükség lenne arra a pontra (pontokra), amelyik AB szakaszra merőleges, és a ABC síkon helyezkedik el, és B pontból indul, és 10 egységnyire van tőle. Előre is köszönet!
|
|
|
|
| [895] Hajba Károly | 2007-10-13 01:03:02 |
 Amilyen arányban növelem a négyzet kerületét, olyan arányban nő az oldalhossza is. Így elég csak az egyik oldalhosszat vizsgálni. Megnövelem 4 méterrel, de ez egyben azt is jelenti, hogy a háromszorosára nőt. Ha valamit háromszorosára növelek, az azt jelenti, hogy még kétszer hozzáadom önmagához (1+2=3). Azaz a 4 méter az eredeti hossz kétszerese, így az eredeti hossz a 4 méter fele, azaz 2 méter.
|
| Előzmény: [894] Emilio, 2007-10-12 23:42:25 |
|
| [894] Emilio | 2007-10-12 23:42:25 |
 Ha egy négyzet olkdalhosszát4m -rel növeljük,kerülete háromszorosára nő.mekkora az eredeti négyzet oldalhossza?
|
|
| [893] HoA | 2007-10-12 20:27:30 |
 Bocs , az utolsó mondat helyesen : "Ekkor az egész A*CB'  és az ennek A*C oldalán fekvő A' pont is f -nek ezen az oldalán van,..." és az ennek A*C oldalán fekvő A' pont is f -nek ezen az oldalán van,..."
|
| Előzmény: [892] HoA, 2007-10-12 20:18:06 |
|
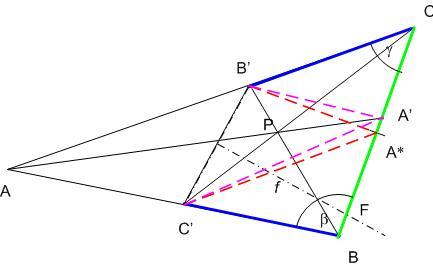
| [892] HoA | 2007-10-12 20:18:06 |
 Belátjuk, hogy ha a  nem egyenlőszárú, pontosabban ha AB nem egyenlőszárú, pontosabban ha AB AC , akkor BC'=CB' és B'A'=C'A' egyszerre nem állhat fenn. Legyen az ABC AC , akkor BC'=CB' és B'A'=C'A' egyszerre nem állhat fenn. Legyen az ABC -ben AC>AB, CB'=BC', BB' és CC' metszéspontja P, PA és BC metszéspontja A'. A Ceva tétel szerint BA'.CB'.AC'=A'C.B'A.C'B CB' = C'B -vel egyszerűsítve BA'.AC'=A'C.B'A . AC>AB miatt B'A>AC' és így A'C<BA' , vagyia A' a BC oldal A* felezőpontja és C között van. -ben AC>AB, CB'=BC', BB' és CC' metszéspontja P, PA és BC metszéspontja A'. A Ceva tétel szerint BA'.CB'.AC'=A'C.B'A.C'B CB' = C'B -vel egyszerűsítve BA'.AC'=A'C.B'A . AC>AB miatt B'A>AC' és így A'C<BA' , vagyia A' a BC oldal A* felezőpontja és C között van.
A C'BA* és az A*CB'  két oldalban megegyezik, de a közrezárt szög - mint az ABC két oldalban megegyezik, de a közrezárt szög - mint az ABC  nagyobb oldalával szemközti szög - az előbbiben ( nagyobb oldalával szemközti szög - az előbbiben ( ) nagyobb mint az utóbbiban ( ) nagyobb mint az utóbbiban ( ) . Ezért a cosinus tétel szerint C'A*>B'A*. A* tehát a B'C' f felező merőlegesének ugyanazon az oldalán van, mint B'. Ekkor az egész A*BC' ) . Ezért a cosinus tétel szerint C'A*>B'A*. A* tehát a B'C' f felező merőlegesének ugyanazon az oldalán van, mint B'. Ekkor az egész A*BC'  és az ennek A*C oldalán fekvő A' pont is f -nek ezen az oldalán van, vagyis B'-höz közelebb, mint C' -höz , A'B'<A'C' , amit bizonyítani akartunk. és az ennek A*C oldalán fekvő A' pont is f -nek ezen az oldalán van, vagyis B'-höz közelebb, mint C' -höz , A'B'<A'C' , amit bizonyítani akartunk.
|
 |
| Előzmény: [889] Gyöngyő, 2007-10-11 17:35:44 |
|
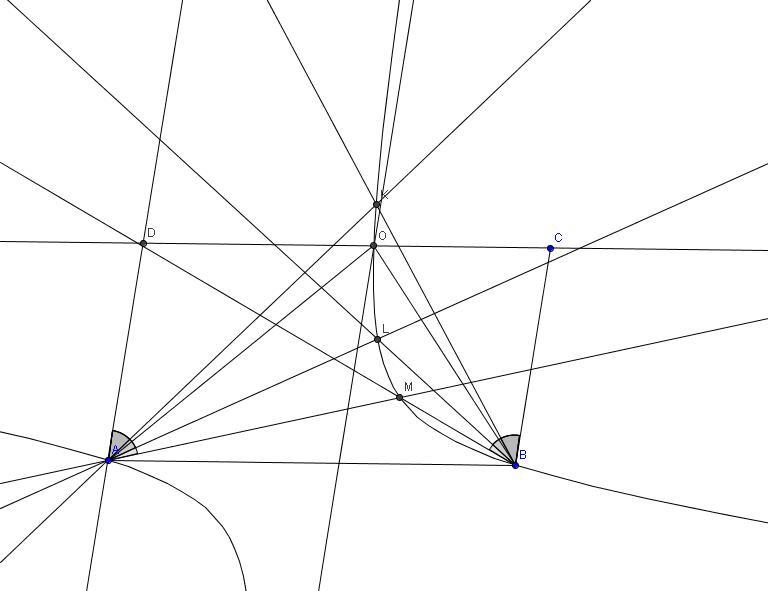
| [891] Sz_Z | 2007-10-11 23:36:42 |
 Itt egy "szerkesztő megoldás", igaz, használ némi projektív geometriát. A [874] hozzászólás alapján olyan egyeneseket keresünk az A és B pontokon keresztül, amelyek "száraktól mért dőlésszöge egyenlő ellentétes irányban" (1), és a metszéspontjuk CD-n van. Az (1) tulajdonságú egyenesek - mivel egymáshoz projektív, A ill. B tartójú sugársorok egymásnak megfelelő egyenesei - metszéspontjai egy hiperbolán vannak, melyre A és B illeszkedik. Ha ennek a hiperbolának három további tetszőleges pontját megszerkesztjük (K, L, M), akkor a hiperbola és a CD egyenes metszéspontjai szerkeszthetőek. (Természetesen ezt a szerkesztést - Steiner-szerkesztés - körzővel-vonalzóval picit hosszabb megcsinálni, mint géppel.)
|
 |
|
| [890] HoA | 2007-10-11 18:08:18 |
 Amíg nem születik igazi szerkesztő megoldás, addig itt van egy , az eddigieknél talán egyszerűbb, számítást követő szerkesztés.
Legyen adva a paralellogramma az AB = a , BC = b oldalhosszakkal és az A-nál lévő  szöggel. Vegyük fel az ABX szöggel. Vegyük fel az ABX  Apollonius körét. Középpontja legyen O, Y-nal szemközti pontja Z. Az XYZ derékszögű Apollonius körét. Középpontja legyen O, Y-nal szemközti pontja Z. Az XYZ derékszögű  ből YZ=d=b/cos ből YZ=d=b/cos , ami adatainkból számítható/szerkeszthető. Mivel az Apollonius kör pontjaira az A-tól és B-től mért távolságok aránya állandó, YB-t x-el jelölve felírható : , ami adatainkból számítható/szerkeszthető. Mivel az Apollonius kör pontjaira az A-tól és B-től mért távolságok aránya állandó, YB-t x-el jelölve felírható :
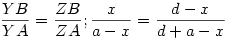
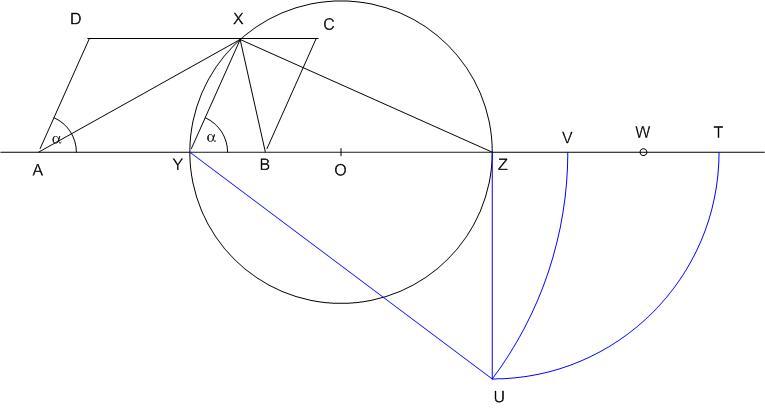
Rendezve x-re másodfokú egyenletet kapunk, melynek megoldása: 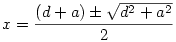 Mivel x a-nál és d-nél is rövidebb, ezért Mivel x a-nál és d-nél is rövidebb, ezért 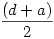 -nél is, tehát csak a negatív előjelet kell figyelembe venni. x szerkeszthető pl így: Vegyük fel a d hosszúságú YZ Z-n túli meghosszabbítására az a hosszúságú ZT szakaszt. Z-ben emeljünk merőlegest YT-re, forgassuk rá Z-ből ZT-t, a metszéspont legyen U. Ekkor -nél is, tehát csak a negatív előjelet kell figyelembe venni. x szerkeszthető pl így: Vegyük fel a d hosszúságú YZ Z-n túli meghosszabbítására az a hosszúságú ZT szakaszt. Z-ben emeljünk merőlegest YT-re, forgassuk rá Z-ből ZT-t, a metszéspont legyen U. Ekkor 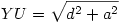 , ezt Y-ból leforgatva YT-re a metszéspont legyen V. Ha W a VT szakasz felezőpontja, VW = WT = x. , ezt Y-ból leforgatva YT-re a metszéspont legyen V. Ha W a VT szakasz felezőpontja, VW = WT = x.
|
 |
| Előzmény: [881] BohnerGéza, 2007-10-10 22:47:04 |
|
| [889] Gyöngyő | 2007-10-11 17:35:44 |
 Sziasztok!
Tudnátok segíteni a következő feladatban:
Adva van egy egy háromszög,felveszünk benne egy p pontot. Összekötjük a csúcsokat a szembelévő oldallal a p ponton keresztül.A metszéspontok rendre A', B',C'. Tudjuk továbbá,hogy C(B)'=B(C)',vmint B'A'=A'C'. Mutassuk meg h a háromszög egyenlőszárú.
Köszönettel: Zsolt
|
|
| [888] titok111 | 2007-10-11 15:47:34 |
 Igen, ezt már tapasztaltam... Sajna nincs semmi ceruza, körző, vonalzó nálam, így csak az ábrába tudok rajzolgatni. Másik tipp: AB oldalra thalés kört rajzolok, és az AB flezőpontján átmenő, BC oldallal párhuzamos egyenesnek a metszéspontja nem esik egybe a keresett egyenessel? (mármint ami A-ból indul és X-be tart?) Vagy ez is speciálisan itt igaz?
|
| Előzmény: [887] SmallPotato, 2007-10-11 13:45:26 |
|
| [887] SmallPotato | 2007-10-11 13:45:26 |
 "Úgy tűnik". Szó szerint. :-((
Semmi nem magyarázza, hogy úgy legyen. Ha elképzelsz egy "derékszögűbb" paralelogrammát, akkor az említett háromszög elannyira nem lesz egyenlőszárú, hogy a két "szár" egy derékszögű háromszög befogója ill. átfogója felé tart (miközben a másik befogó nagyon nem nulla).
Az eredeti hozzászólás ábrája eléggé spécire sikeredett, mert a paralelogramma hegyesszöge kb 60 fokos, emellé az AX' és az AD hossz is közel egyforma. De ezek tök esetleges dolgok.
|
| Előzmény: [885] titok111, 2007-10-11 13:28:37 |
|
| [886] titok111 | 2007-10-11 13:40:23 |
 No meg (de ez gondolom nem nagy felfedezés..) ha az AD oldalegyenest metszük a BX egyenesével (P pont), a BC oldalegyenest az AX egyenessel (Q pont) Akkor ABPQ egy trapéz, amelynek átlói X pontban metszik egymást.
|
| Előzmény: [884] SmallPotato, 2007-10-11 13:16:58 |
|
| [885] titok111 | 2007-10-11 13:28:37 |
 Szerintem lehet, hogy benéztem... Viszont úgy tűnik, (ha az eredeti ábrát nézzük (868 sz. hozzászólás itt)), hogy ha behúzzuk a paralelogramma középvonalát, akkor ahol metszi az xx'egyenest (legyen P pont), akkor ha a BP egyenest elmetszük az AD oldalegyenessel, egy egyenlőszárú háromszöget kapunk. Nem?
|
| Előzmény: [884] SmallPotato, 2007-10-11 13:16:58 |
|
| [884] SmallPotato | 2007-10-11 13:16:58 |
 Ha jól értelmezem a leírásod, akkor ha a paralelogramma egy téglalaphoz tart, a megoldásod szerinti X pont a CD oldal C felőli negyedelőpontjához tart. Ez viszont így nem lehet jó; ha a paralelogramma derékszögű, úgy a helyes megoldás a CD oldal felezőpontja.
Rosszul értettem valamit? Próbálj egy ábrát berakni!
|
| Előzmény: [883] titok111, 2007-10-11 12:08:48 |
|
| [883] titok111 | 2007-10-11 12:08:48 |
 Bármelyik paralelogrammában: az alapot helyén hagyva csinálj egy téglalapot, amelynek oldala megegyzik az eredeti paralelogrammáéval. Ennek felső oldalát felezd el, majd az alsó oldalegyenest jobbra (most) hosszabbítsd meg, mérd fel rá a rövidebb oldalt.ezt és a téglalap fleső oldalát felező pontot kösd össze. Ahol metszi a paralelogramma tetjét, attól jobbra eső szakaszt felezd el, és megvan a X pont.
|
| Előzmény: [882] BohnerGéza, 2007-10-10 23:57:14 |
|
|
|
|
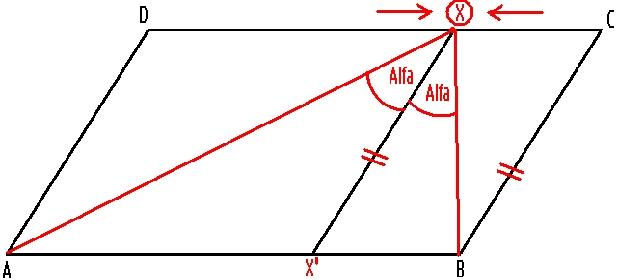
| [879] bohmajster | 2007-10-10 17:53:35 |
 Esetleg átlehetne fogalmazni a feladatot: szerkesszük meg AL és BK félegyenest, úgy hogy dőlésszögük ugyanakkora legyen ellentett irányban, és metszetük a CD-n legyen rajta.
|
 |
|
|
|
|
|
|
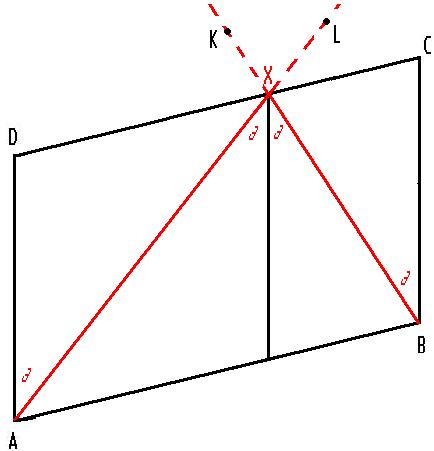
| [873] bohmajster | 2007-10-09 22:58:15 |
 Üdv mindenkinek, már jó pár napja töröm magam egy feladaton, de nem tudom megoldani a problémát. Gondoltam megosztom veletek is:
Adott ABCD paralelogramma. Megkell szerkeszteni X-et a CD-n, úgy hogy érvényes legyen: AXX' szög ugyanakkora mint X'XB és X'X párhuzamos AD-vel. (az ábra szerint)
Várom a hozzászólásokat...
|
 |
|
|
| [871] SmallPotato | 2007-10-07 11:47:14 |
 Néhány kiegészítés:
1.) Az eredeti 123. feladatban a hatványvonal a k1 és k2 érintési pontjában húzható közös érintő.
2.) Az előző hsz-ban leírt bizonyítás a rajzolt viszonyokon túl kiterjed az egymást érintő és az egymást metsző k1 és k2 körök esetére is. Ezekben az esetekben a hatványvonal rendre k1 és k2 közös belső érintője (értelemszerűen a körök egyetlen közös pontján át), ill. a körök metszéspontjain át húzható egyenes.
3.) Ha k1 és k2 nem érinti egymást, akkor (akár 0, akár 2 közös pontjuk van) az általuk "közrefogott" C1C2 átmérőjű körhöz G pontban húzható érintő is természetesen párhuzamos e-vel, e1-gyel és e2-vel. G aszerint helyezkedik el a közös átmérőegyenesnek a D felőli ill. azzal ellentétes oldalán, hogy k1 és k2 közös pontjainak száma 2 vagy 0.
|
| Előzmény: [870] SmallPotato, 2007-10-07 01:14:42 |
|
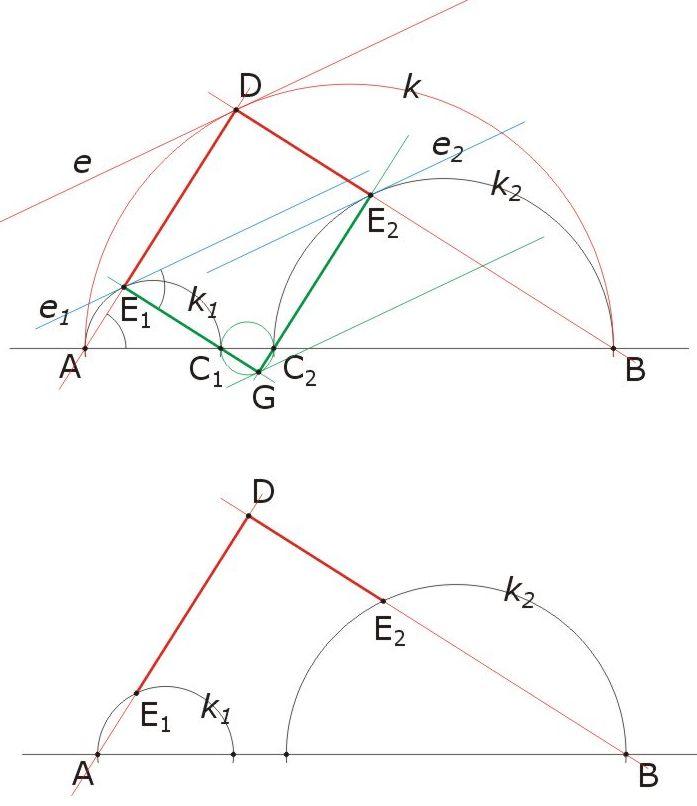
| [870] SmallPotato | 2007-10-07 01:14:42 |
 Megoldás a 124. feladatra.
Rajzoljunk egy - szándékosan "elrontott" - ábrát, azaz egy olyat, ahol a találomra választott D pontból húzott DA és DB egyenesek által a k1 ill. k2 körökből kimetszett E1 és E2 pontok nem a közös érintő érintési pontjai!
Ebből az ábrából is megállapíthatjuk a következőket:
1.) Ha D a k kör pontja, akkor a jelölt e, e1 és e2 érintők párhuzamosak, hiszen k1-et A-ból, k2-t B-ből kellő arányban nagyítva a k1 ill. k2 körök k-ba, az E1 ill. E2 pontok D-be, tehát az e1 ill. e2 egyenesek e-be mennek át.
2.) A Thalész-tétel megfordítása értelmében az AC1E1, ABD és C2BE2 háromszögek derékszögűek (így hasonlóak is), és a vastagítva rajzolt DE1GE2 négyszög téglalap.
3.) A jelölt C1AE1 és C1E1e1 szögek egyenlőek, mert mindkettő a k1 kör C1E1 ívén nyugvő kerületi szög (utóbbi érintőszárú).
4.) Ezek szerint e1 és e2 akkor esik egybe, ha a jelzett DE1GE2 téglalapban pl. az E2E1D szög a jelzett szög pótszöge, azaz - a korábban említett háromszög-hasonlóságokat figyelembe véve - ha pl. 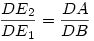 . .
Az utóbbi egyenlőséget átrendezve (az alsó ábrán csak a lényeg van kiemelve): DB*DE2=DA*DE1, azaz e1 és e2 akkor és csak akkor esik egybe, ha a D pont hatványa a k1 és k2 körökre azonos. Ez akkor és csak akkor teljesül, ha D pont a k1 és k2 körök hatványvonalán van. A hatványvonal ismert tulajdonsága, hogy adott pontjából a két körhöz egyenlő hosszú érintőszakaszok húzhatók (ha egyáltalán húzhatók), tehát (egyebek közt) a 124. feladat eredeti ábráján az F pontból is.
|
 |
| Előzmény: [857] BohnerGéza, 2007-09-20 11:08:40 |
|
| [869] farkasb | 2007-10-05 03:01:23 |
 Köszönöm, ez a 3. megoldás nagyon jó! Persze elismerésem a másik kettőért is :)
|
|
| [867] HoA | 2007-10-04 17:01:42 |
 Tovább egyszerűsíthető a megoldás, ha a koordinátarendszer kezdőpontját x0 -ba helyezzük át. Ekkor a  két oldalvektora a=x1-x0=(-0,1693;-0,7763;-1,7028) és b=x2-x0=(-2,7655;-1,4626;0,8991) . A két oldalvektora a=x1-x0=(-0,1693;-0,7763;-1,7028) és b=x2-x0=(-2,7655;-1,4626;0,8991) . A  síkját e két vektor feszíti ki, így R felírható síkját e két vektor feszíti ki, így R felírható
R=x.a+y.b..........(1)
alakban. R az oldalfelező merőlegeseken van, tehát (R-0)a=(a-R)a , a(2R-a)=0 és hasonlóan b(2R-b)=0 . (1) -ből R felbontását a két utóbbi egyenletbe helyettesítve és rendezve kapjuk:
2.a2.x+2.ab.y=a2 ; 2.ab.x+2.b2.y=b2
Látható, hogy a numerikus számításhoz csak az a2,b2 és ab értékekre van szükségünk, ezek rendre 3,53083202 ; 10,59556982 ; 0,07262805 . A megoldás - például az egyenlő együtthatók módszerével
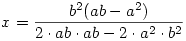 ; ; 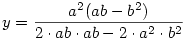
Numerikusan x = 0,489784223 ; y = 0,496642741 , amiből R = (-1,45639 ; -1,10661 ; -0,38747 ) . Visszatérve az eredeti koordináta rendszerre ezt x0 -hoz hozzáadva a várható r=(0,037714;-0,96211;0,532327) eredményt kapjuk.
|
| Előzmény: [866] jonas, 2007-10-04 11:57:49 |
|
| [866] jonas | 2007-10-04 11:57:49 |
 Most nézzük ugyanerre az egyszerűbb megoldást.
Legyen tehát a háromszög három csúcsába mutató vektor
x0=(1.4941,0.1445,0.9198)
x1=(1.3248,-0.6318,-0.7830)
x2=(-1.2714,-1.3181,1.8189)
Egyszerűen kiszámoljuk két csúcs felezőmerőleges síkját, aztán egy másik két csúcs felezőmerőleges síkját is (a harmadik nem kell), majd a csúcsok síkját, végül ezek metszetét.
Az a és b pontok felezőmerőleges síkjának egyenpete 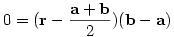 , átalakítva r(b-a)=(a+b)(b-a)/2. , átalakítva r(b-a)=(a+b)(b-a)/2.
Speciálisan a x0 és x1 csúcsok felezőmerőleges síkjának koordinátái
x1-x0=(-0.1693,-0.7763,-1.7028)
(x0+x1)(x1-x0)/2=-0.1659
Hasonlóan x1 és x2 csúcsoké
x2-x1=(-2.5962,-0.6863,2.6019)
(x1+x2)(x2-x1)/2=1.9474
A három csúcs síkját pedig egy 4 méretű homogén lineáris egyenletrendszerből kapjuk meg. Ha a sík egyenlete pr=q, akkor ebben xi rajta fekszik, így 0=pxi-q, amit meg kell oldani a p,q négy változóra. Ennek a megoldását például a Cramer-szabályból kapjuk meg: q a csúcsokból álló mátrix determinánsa, p pedig azoknak a mátrixoknak a determinánsa, amit ez előbbi mátrixból egy oszlop 1-re cserélésével kapunk.
p=(-3.1885,4.8613,-1.8992)
q=-5.8084
Most már csak el kell metszenünk a három síkot. Ehhez az alábbi egyenletrendszerünk van:
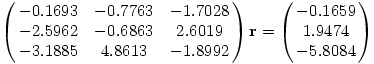
Ezt megoldva
r=(0.0377,-0.9621,0.5323)
ami szépen egyezik az előző megoldással.
|
|
|
| [864] jonas | 2007-10-02 16:57:08 |
 Nézzünk egy példát.
Vegyük azt a háromszöget, aminek a csúcsainak koordinátái
x0=(1.4941,0.1445,0.9198)
x1=(1.3248,-0.6318,-0.7830)
x2=(-1.2714,-1.3181,1.8189)
Ekkor az oldalak vektorai
v0=x1-x2=(2.5962,0.6863,-2.6019)
v1=x2-x0=(-2.7655,-1.4626,0.8991)
v2=x0-x1=(0.1693,0.7763,1.7028)
Most számoljuk ki az oldalak által bezárt szögeket az oldalvektorok skalárszorzatából.
|v1|=3.25512
|v2|=1.87908
(v1,v2)=-0.0726366
cos ( - - 0)=(v1,v2)/(|v1|.|v2|)=0.0118753 0)=(v1,v2)/(|v1|.|v2|)=0.0118753
 - - 0=1.58267 0=1.58267
 0=1.55892 0=1.55892
Hasonlóan
 1=1.05618 1=1.05618
 2=0.52649 2=0.52649
Ebből
sin (2 0)=0.0237489 0)=0.0237489
stb, amiből a körülírt kör középpontjába mutató vektor
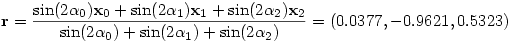
Ennek a távolsága valóban minden csúcstól ugyanannyi:
r=|r-x0|=|r-x1|=|r-x2|=3.49585
és a r-bfxi vektorok lineárisan összefüggők, azaz a pont a háromszög síkjában van, tehát ez valóban a háromszög középpontja.
|
| Előzmény: [863] jonas, 2007-10-02 15:37:50 |
|
| [863] jonas | 2007-10-02 15:37:50 |
 Igen, noha fejből nem tudtam megmondani. Súlyozni kell a csúcsokat a csúcsban lévő szög kétszeresének a színuszával, és normálni ezeknek az összegével.
|
| Előzmény: [861] farkasb, 2007-10-02 00:06:56 |
|
| [862] Lóczi Lajos | 2007-10-02 13:29:35 |
 Minden attól függ, hogy milyen matematikai szövegkörnyezetben vagyunk. Pl. a háromszög is tekinthető körnek (és viszont), ha topológiai szemmel nézzük a dolgokat, ahol is csak a folytonos egymásba deformálhatóság számít.
|
| Előzmény: [860] Pokolfajzat, 2007-10-01 20:21:37 |
|
| [861] farkasb | 2007-10-02 00:06:56 |
 Tisztelt Fórumozók!
Érdeklődnék, hogy valaki tud-e képletet egy egy térbeli háromszög köré írható kör középpontjának kiszámítására, és a térbeli kör egyenletének felállítására. Előre is köszönettel: F.Balázs
|
|
| [860] Pokolfajzat | 2007-10-01 20:21:37 |
 Nincs különösebb jelentősége, csak részemről volt ez egy feltevés, másoknak. Akik azt mondták erre, hogy ez nem igaz, csakhogy az igazamat én sem tudtam ésszerűen alátámasztani. És reméltem, ha a feltevésem igaz akkor itt talán tudnak rá egyesek magyarázatot is adni.
|
|
|
| [858] Pokolfajzat | 2007-09-22 19:44:13 |
 Csak egy kérdéssel zavarnám meg a tisztes társaságot. Előre is elnézést kérek, ha banális vagy ostoba lenne a kérdés. Tekinthető e a kör egy végtelen sokszögnek? Előre is köszönöm.
|
|
|
| [856] SmallPotato | 2007-09-20 08:39:23 |
 Felhozom kicsit a topikot.
A 123. feladat megoldása:
Kicsinyítsük az AB átmérőjű kört A-ból 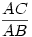 arányban! Ekkor a D pont képe E, AB kör D-beli érintőjének képe pedig AC kör E-beli érintője lesz; e két érintő (a kicsinyítés tulajdonságaiból adódóan) párhuzamos. arányban! Ekkor a D pont képe E, AB kör D-beli érintőjének képe pedig AC kör E-beli érintője lesz; e két érintő (a kicsinyítés tulajdonságaiból adódóan) párhuzamos.
A 120-as feladat megoldásából azonban ismert, hogy a rajzolt elrendezésben az AB kör D-beli érintője párhuzamos az AC és a CB körök közös külső érintőjével. Eszerint AC kör imént előállt (E pontbeli) érintője ezzel a közös érintővel egybeesik.
(Természetesen elindulhattunk volna az AB kört C-ből 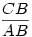 arányben kicsinyítve is.) arányben kicsinyítve is.)
|
| Előzmény: [854] BohnerGéza, 2007-09-05 23:57:21 |
|
|
|
| [853] sakkmath | 2007-08-30 09:20:48 |
 Köszönöm, hogy foglalkoztál a feladattal és feltetted a megoldásodat, ami természetesen helyes.
A feladat egyébként - elemi módon - még (legalább) két másik módszerrel is megoldható. Tehát nincs még lelőve semmi, aki esetleg új megoldásra bukkan, nyugodtan tegye fel...
|
| Előzmény: [851] SmallPotato, 2007-08-29 23:34:51 |
|
|
| [851] SmallPotato | 2007-08-29 23:34:51 |
 A 808-asra hoznék egy megoldást; úgy látom, eddig még nem érkezett.
Legyen 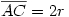 , és , és 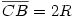 . .
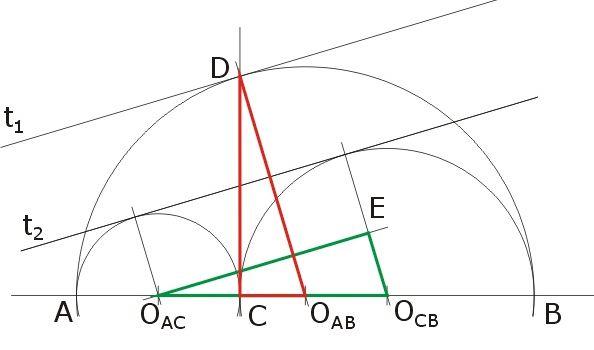
Húzzunk párhuzamost t2-vel az OAC ponton át; messe ez a BC átmérőjű körnek a t2-vel való érintési pontjába húzott sugarát az E pontban. Ekkor 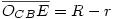 és az OACOCBE háromszög E szöge derékszög, átfogója pedig R+r. és az OACOCBE háromszög E szöge derékszög, átfogója pedig R+r.
Az OABDC háromszög C szöge derékszögű, 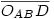 átfogója (lévén az átfogója (lévén az  átmérőjű kör sugara) szintén R+r, és átmérőjű kör sugara) szintén R+r, és 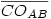 befogója szintén R-r, tehát befogója szintén R-r, tehát
az OACOCBE és a OABDC háromszögek egybevágók.
Eszerint viszont COABD =OACOCBE =OACOCBE , azaz , azaz 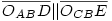 , és mivel az érintők merőlegesek a megfelelő sugarakra, t1||t2. , és mivel az érintők merőlegesek a megfelelő sugarakra, t1||t2.
|
 |
| Előzmény: [808] sakkmath, 2007-07-16 18:26:43 |
|
| [850] zizibi | 2007-08-24 18:31:31 |
 Köszönöm, segítséget. Így már értem.
Az az igazság ogy a 10. volt már majd 10 éve volt, de nem is azzal van a gond csak nem esett le az egyenlő együtthatók módszer.
Mégegyszer köszönöm! :)
|
| Előzmény: [849] BohnerGéza, 2007-08-24 16:29:24 |
|
| [849] BohnerGéza | 2007-08-24 16:29:24 |
 A számolásnál az egyenlő együttgatók módszerét használtam. Ha elvégezted volna a jelzett számolást, észrevetted volna, hogy y kiesik.
Próbáld ki! Az első egyenletet v2-vel, a másodikat v1-gyel szorozva, a kettőben x ua-szor lesz. Kivonva egymásból a kapott egyenleteket x kiesik, y kiszámolható.
Természetesen behelyettesítéssel is kijön ue.
Ezeket legalább tizedikes ismerőseidtől is megtudhattad volna.
|
| Előzmény: [848] zizibi, 2007-08-24 09:41:49 |
|
| [848] zizibi | 2007-08-24 09:41:49 |
 Hát igen, én bonyolultabban akartam megoldani :)
De azt nem igazán értem, hogy ha megszorzom az egyik egyenletet v1 a másikat v2-vel, akkor hova tűnik az y? Mert hát ha jól emlékszem, hiányos matektudásomban az van, hogy minden tagot szorozni kell, vagy nem? Ez valamiféle egyszerűsítés?
Elnézést, hogy ennyit értetlenkedem, de szeretném megérteni hátha jobban felfogom...
|
| Előzmény: [846] BohnerGéza, 2007-08-23 14:09:27 |
|
|
|
| [845] zizibi | 2007-08-23 11:33:56 |
 Igen, erre az egyenletre rá jöttem én is, de kéne még egy egyenlet, gondolom, amiből ki lehet fejezni az x-t és egy másik amiből az y-t.
Na idáig nem jutottam el. Vagy az egyik koordinát egyenletét be lehetne helyettesíteni a másikba, pl. x-et kifejezve belőle?
|
| Előzmény: [842] BohnerGéza, 2007-08-22 20:45:22 |
|
|
|
|
| [841] zizibi | 2007-08-22 14:26:32 |
 Kedves BohnerGéza!
Még egyszer köszönöm az előző segítséget, remekül tudom használni (bár koordinátarsz-re nem volt szükségem, mert karakteresen működik a program), de nem igazán értem, hogy Pithagórasz-tétel hogyan is működik ebben az esetben.
Közben pedig újabb problémába ütköztem.
Szintén koordináta jellegü és az előző feladat megfordítása, vagyis adott AB egyenes és egy X pont. Meg szeretném tudni, hogy az X pont milyen merőleges távolságra van A-tól, AB egyenesen mérve illetve milyen messze van AB egyenestől.
Szögfügvényekkel találtam megoldást, de nekem jobban tetszene egy, az előzőhöz hasonló megoldás.
Előre is köszönöm a segítséget!
|
| Előzmény: [836] BohnerGéza, 2007-08-16 21:56:13 |
|
|
|
| [838] Bauer Gábor | 2007-08-21 09:53:03 |
 Tisztelt Barátaim! Alapvetó problémával kerültem szembe a következő feadattal: "Szerkesszünk szabályos háromszöget ha adott a beírt kör sugara." Kérdésem a következő: Melyek azok a tételek amelyek átgondolásával a feladat megoldható és mi a szerkesztés menete? Válaszukat hálásan köszönöm.
|
|
|
