| [331] Chryst | 2006-01-08 10:59:05 |
 Jézusom!!!
Megvan a megoldás!!! És nagyon egyszerű. Csak nem értem, hogy eddig egyedül, magamtól hogy nem jöttem rá.
Leírom:
(x-u)2+(y-v)2=r2
rendezgetek egyet:
(x-u)2=r2-(y-v)2
gyököt vonok:
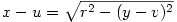
megint rendezkedek, és már ki is derül milyen apróság nem jutott eddig eszembe:
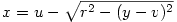
Hát igen, ismételten beigazolódott: "Az igazi zseniknek a legegyszerűbb dolgok jelentik a legnagyobb problémát" :)
A segítséget azért köszönöm
|
|
| [330] Chryst | 2006-01-08 10:21:14 |
 Köszönöm, de ilyesmiket én is kihoztam, csak mindegyikkel ugyanaz az egy baj volt:
x2-2xu+u2+(y-v)2-r2=0
Ebből ugyebár ezt kapom:
x2=2xu-u2-(y-v)2+r2 vagy x2-2xu=r2-u2-(y-v)2
Ez nekem azért rossz, mert ha én a programmal az x-et akarom kiszámoltatni, akkor az x csak egyszer szerepelhet az egyenletben, méghozzá x=? helyen.
Ezekben az egyenletekben szerintem első problémát az jelenti, hogy az egyik x előtt van egy u szorzó. Megpróbáltam eltenni máshová azt az u-t, de akkor meg az x2 alá került, valahogy így:
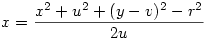
és ez nekem már megint nem jó, mert onnan az x2-et még annyira sem tudom kivenni.
Lényegében nekem egy olyan egyenlet kell, mint amit akkor csinálunk, amikor több ismeretlenes egyenleteket számoltunk azzal a módszerrel, hogy az egyik ismeretlent kifejezem, amit meg kapok, azt behelyettesítem a másik egyenletbe. Amikor így fejezem ki az egyik ismeretlent, akkor nem szerepelhet a másik oldalon is az az ismeretlen, mert akkor nem tudnám kiszámolni a másik ismeretlent.
Szóval nekem egy ilyen egyenletre (vagy inkább képletre) lenne szükségem.
Nem akarok kört rajzolni, csak azt akarom megvizsgáltatni, hogy egy, a képernyőn elhelyezkedő pont egy bizonyos (előre megadott) körön belül van-e. Szóval szerintem mindenféleképpen ezzel az egyenlettel célszerű számolnom.
Tudom, hogy ezzel a képlettel még csak egy kör körvonalát kapom meg, de egyelőre még nem akartam egyenlőtlenséggel számolni, (ezzel: (x-u)2+(y-v)2<r2) mert ezzel ráérek majd akkor foglalkozni, amikor a progit írom. Ha egy kör körvonala megvan, az már fél siker, kiindulásnak elég lesz.
A további segítségeket előre is köszönöm
|
| Előzmény: [329] 2501, 2006-01-08 02:59:52 |
|
| [329] 2501 | 2006-01-08 02:59:52 |
 (x-u)2+(y-v)2=r2
x2-2xu+u2+(y-v)2-r2=0
Innen mar remelem megy egyedul is. :)
(Lesz benne gyokvonas. Ha kort kell rajzolni, akkor vannak ennel sokkal hatekonyabb eljarasok.)
|
| Előzmény: [328] Chryst, 2006-01-07 22:19:47 |
|
| [328] Chryst | 2006-01-07 22:19:47 |
 Programozok, és egy programban szeretnék kipróbálni valamit, amihez (koordináta geometriában) a kör egyenletéből ki kellene fejeznem az x-et, de egyedül nem tudok értelmes (aránylag egyszerűnek mondható) választ csinálni az "x=?" kérésre... Sőt! Egyáltalán nem tudok semmit kihozni x-re. Ha valaki segítene, annak nagyon örülnék.
Előre is nagyon köszönöm.
Ha valaki segítene, de hirtelen nem jut eszébe az egyenlet, annak mellékeltem ábraként. (A körvonal bármely P(x;y) pontja C(u;v) középponttól adott r távolságra van.) (Csakhogy precízek legyünk :)
Mégegyszer köszönöm.
|
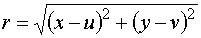 |
|
| [327] Iván88 | 2006-01-06 15:20:39 |
 Ez van. Ez a sejtés nem jött be. (Közben én is rájöttem, a koszinusz-tételből) Pedid olyan szépen hangzott :-(
A matemetikus halála az, amikor egy szép sejtést tönkretesz egy csúnya tény.
|
| Előzmény: [326] jonas, 2006-01-06 13:28:16 |
|
| [326] jonas | 2006-01-06 13:28:16 |
 Nem igaz.
Egyrészt azért, mert ha a b, akkor a paralellogrammát lapítva az átlók által bezárt szög is akármilyen lapos lehet. b, akkor a paralellogrammát lapítva az átlók által bezárt szög is akármilyen lapos lehet.
Másrészt ha a paralellogramma két szomszédos csúcsát rögzíted, és a másik kettőt mozgatod (úgy, hogy az oldalhosszak rögzítettek), akkor a középpont egy körön mozog. Az átlók szöge akkor lenne állandó, ha ez a kör a rögzített oldal egy látóköre lenne, de nem az, mert a középpont nem megy a rögzített csúcsok közelébe.
|
| Előzmény: [325] Iván88, 2006-01-05 15:58:13 |
|
| [325] Iván88 | 2006-01-05 15:58:13 |
 Igaz e, hogy az adott a, b oldalú paralelogrammákban (nem rombusz) az átlók által bezárt szög állandó? (a, b rögzített érték, az oldalak szögét változtatjuk.)
|
|
|
|
| [322] philip | 2005-12-03 22:25:32 |
 Hogyan bizonyítjuk a Fauerback-kört (kilencpont-köre)?
|
|
| [321] Róbert Gida | 2005-11-30 20:30:07 |
 63. feladat
Adott a síkon egy kör, melyek azok a legkisebb területű ellipszisek, melyek tartalmazzák a félkört? Igaz-e hogy az ellipszis területe kisebb, mint a kör területe?
Az egyszerűsítések érdekében feltehetjük, hogy a kör és az ellipszis középpontja ugyanazon a koordináta-tengelyen van és az ellipszis megfelelő tengelyei párhuzamosak a koordináta-tengelyekkel.
Ugyanez a kérdés magasabb ( n ) dimenzióban. Melyek azok az n dimenziós ellipszoidok melyek tartalmazzák az n dimenziós félgömböt, úgy hogy az ellipszoid térfogata minimális legyen, ez a térfogat kisebb-e mint a gömb térfogata? Ugyanazon egyszerűsítéseket most is feltehetjük mint előbb a tengelyekre vonatkozóan.
|
|
|
| [319] lorantfy | 2005-11-30 09:14:39 |
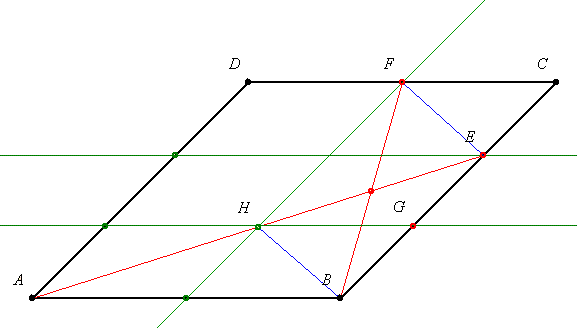
 A legprimitívebb módszer, hogy párhuzamosokat húzunk a felező és harmadoló pontokból az oldalakkal. AE felezőpontja H. Aztán BEFH paralelogramma átlói felezik egymást.
|
 |
| Előzmény: [318] philip, 2005-11-29 19:51:23 |
|
| [318] philip | 2005-11-29 19:51:23 |
 Köszönöm szépen a segítséget! Lenne mégegy feladatom: Az ABCD négyszög paralelogramma,amelynek BC oldalát az E pont harmadolja úgy,hogy E C-hez van közelebb,az F pedig a DC oldalt felezi.Bizonyítsuk be,hogy a BF szakasz az AE szakaszt negyedeli,az AE a BF szakaszt felezi!
|
|
| [317] jonas | 2005-11-24 10:11:26 |
 Hmm. A 18 tényleg rossz.
Akkor x=1/(1/b+1/c)=8.
Ez onnan jön ki, hogy az FEC és a DBE háromszög hasonló az ABC-hez, mert az oldalaik párhuzamosak, így aztán a CE szakasz ax/c, az EB szakasz ax/b, amiből a=ax/c+ax/b.
|
| Előzmény: [316] lorantfy, 2005-11-24 08:11:52 |
|
|
|
| [314] philip | 2005-11-23 17:43:45 |
 Sziasztok! Az alábbi feladat megoldásában szeretnék segítséget kérni:
1.Egy háromszög oldalainak hossza c=24 a=18 b=12.Írjunk bele olyan rombuszt,amelynek egyik csúcsa az A,a többi csúcsa a háromszög oldalaira illeszkedik.
Eéőre is köszönöm!
|
|
| [313] nadorp | 2005-11-22 12:09:49 |
 Azt hiszem van valami a szimplexre. Először belátunk egy állítást:
Legyenek a,b,c pozitív számok, min(a,b,c)=a, b c Ekkor léteznek olyan x,y,z pozitív számok,hogy x<a, c Ekkor léteznek olyan x,y,z pozitív számok,hogy x<a,
x+y+z=a+b+c
x2+y2+z2=a2+b2+c2,továbbá xyz<abc is teljesül. Biz:
Az egyenletrendszer ekvivalens az alábbival ( ):
y+z=a+b+c-x
y2+z2=a2+b2+c2-x2,azaz
yz=x2-(a+b+c)x+(ab+ac+bc).
Egy kis számolással adódik, hogy a fenti egyenletrendszer olyan másodfokú egyenletre vezet, melynek diszkriminánsa b c esetén alkalmas x<a-ra pozitív,ezért a fenti egyenletrendszernek létezik ezzel az x-szel y,z pozitív megoldása.Már csak az abc>xyz egyenlőtlenséget kell belátni. c esetén alkalmas x<a-ra pozitív,ezért a fenti egyenletrendszernek létezik ezzel az x-szel y,z pozitív megoldása.Már csak az abc>xyz egyenlőtlenséget kell belátni.
xyz=x3-(a+b+c)x2+(ab+ac+bc)x=f(x). Mivel f(0)=0 és f(a)=abc, ezért ha bebizonyítjuk, hogy f(x) a [0,a]-n monoton, akkor kész vagyunk. Ehhez elég belátni, hogy a derivált függvény gyökei nagyobb egyenlőek, mint a. Ez egy kis számolással a (b-a)(c-a) 0 nyilvánvaló egyenlőtlenségre vezet. 0 nyilvánvaló egyenlőtlenségre vezet.
Az eredeti feladat ezek után egyszerű. Ha
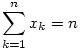 és és
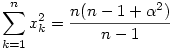 , akkor , akkor
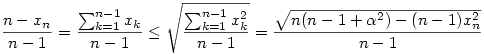 ,ebből ,ebből
xn 1- 1- . A fenti állításból következik, hogy a koordináták szorzata akkor minimális, ha valamelyik xi éppen 1- . A fenti állításból következik, hogy a koordináták szorzata akkor minimális, ha valamelyik xi éppen 1- , a többi pedig egyenlő.Ez viszont nem lehet más,mint , a többi pedig egyenlő.Ez viszont nem lehet más,mint 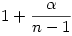
|
|
| [312] Lóczi Lajos | 2005-11-21 20:35:48 |
 Eddig mi már beláttuk az a.) pontot, sőt annál többet is: a szorzat a minimumot/maximumot olyan pontokban veszi fel (és nem csak "veheti"), ahol az xi számok pontosan 2 különböző értéket vesznek fel, l. a Lagrange multiplikátoros (valamint kompaktsági) érvelést.
A b.) rész n=3-ra a [302]-es hozzászólás-beli utolsó képletemből szinte triviális, két polinomot kell összehasonlítani, a k=2 érték minden  >0 esetén kisebb, mint a k=1-hez tartozó. >0 esetén kisebb, mint a k=1-hez tartozó.
Hiányzik a c.) rész, valamiféle induktív érvelés kellene tehát. Ha ez meglenne, akkor
ezek alapján a d.) kérdésre is pozitívan válaszoltunk.
Mindenesetre rögtön adódott egy szép és nehéz egyenlőtlenség a [302]-es végéről. Ha n nagy, akkor annak a függvénynek a képe "kotangens" jellegű, ilyen típusú függvényekről pedig tudom, hogy meggyűlt velük már a bajom :)
|
| Előzmény: [311] Róbert Gida, 2005-11-21 19:49:09 |
|
| [311] Róbert Gida | 2005-11-21 19:49:09 |
 Nem úgy látom be, segítség a 61. feladathoz:
62. feladat
a. Legyen a és b rögzített pozitív valós számok és n>1 pozitív egész, ahol 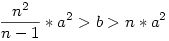 . Legyen . Legyen 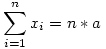 és és 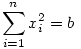 ,x=(x1,x2,...,xn) ,x=(x1,x2,...,xn) 0 , akkor 0 , akkor 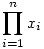 a minimumot olyan pontban veheti csak fel, ahol az xi-k pontosan két különböző értéket vesznek fel. a minimumot olyan pontban veheti csak fel, ahol az xi-k pontosan két különböző értéket vesznek fel.
b. Bizonyítsuk be, hogy n=3-ra a minimumot olyan pontban veszi fel, ahol 2 darab xi megegyezik, a külöböző pedig kisebb.
c. Bizonyítsuk be n>3-ra, hogy a minimumot olyan pontban veszi fel, ahol (n-1) darab xi megegyezik, a különböző pedig ettől kisebb.
d. Ezzel bebizonyítottuk-e a 61. feladatot?! Ha igen akkor miért?
|
| Előzmény: [310] Lóczi Lajos, 2005-11-21 13:08:17 |
|
| [310] Lóczi Lajos | 2005-11-21 13:08:17 |
 Legalább már "látjuk" a kontextust, de ezzel nem jutottunk közelebb a megoldáshoz :)
Azt kérdezném még, hogy be tudnád-e látni a [302]-es hozzászólás végén szereplő kifejezésről, hogy k-ban szigorúan monoton fogy (vagy várom a másik utat, hogy anélkül hogyan tudjuk minimalizálni a szorzatot...)
|
| Előzmény: [309] Róbert Gida, 2005-11-21 07:11:15 |
|
| [309] Róbert Gida | 2005-11-21 07:11:15 |
 Ez a lineáris programozási feladatnak Karmarkar féle projektív módszeréhez kell ez az állítás. Konkrét tétel ( neve is van ) ez az állítás a projektív módszernél. Projektív módszer egy polinomiális futás idejű algoritmus, ellentétben a szimplex módszerrel a lineáris programozási feladatokra. Módszer lényege, hogy trafókkal eléri, hogy min(x1) ahol 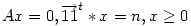 -t kell meghatározni, tehát pont a mi szimplexünkőn dolgozik, egy hipersíkkal elmetszve, ráadásul úgy, hogy egy lépésben ezt az -t kell meghatározni, tehát pont a mi szimplexünkőn dolgozik, egy hipersíkkal elmetszve, ráadásul úgy, hogy egy lépésben ezt az  *r sugarú gömböt is használva egy kisebb x1 értékkel rendelkező megengedett megoldást talál és úgy transzformálja a feladatot, hogy újra ebbe a szimplexbe viszi a feladatot ( az A más lesz ) a megengedett megoldást pedig a gömb középpontjába, ami a csupaegy vektor. *r sugarú gömböt is használva egy kisebb x1 értékkel rendelkező megengedett megoldást talál és úgy transzformálja a feladatot, hogy újra ebbe a szimplexbe viszi a feladatot ( az A más lesz ) a megengedett megoldást pedig a gömb középpontjába, ami a csupaegy vektor.
Ha kell akkor tovább bontom a feladatot.
|
| Előzmény: [308] Lóczi Lajos, 2005-11-20 19:34:22 |
|
| [308] Lóczi Lajos | 2005-11-20 19:34:22 |
 Az extremizálandó xi-szorzatnak szerintem az az érdekessége (és ez ellentmond a szemléletnek), hogy éppen akkor lesz minimális, ha a lehető legtöbb szám egynél nagyobb benne és csak 1 db lesz 1-nél kisebb; illetve akkor maximális az értéke, ha (n-1) db kisebb 1-nél és csak 1 db nagyobb 1-nél közülük.
Majd megkérdezzük Róbert Gidát, hogy honnan szedte ezt a feladatot, biztosan nem "csak úgy" kitalálta :)
|
| Előzmény: [307] nadorp, 2005-11-20 18:59:58 |
|
|
| [306] Lóczi Lajos | 2005-11-20 18:53:07 |
 [A Lagrange-multiplikátoros módszerhez a teljesség kedvéért hozzá kell tenni, hogy ugye ott lehetnek szélsőértékpontok, ahol a célfüggvény és a feltételi függvények deriváltjainak (multiplikátorokkal vett) lineáris kombinációja a nullvektor, VAGY OTT, ahol a feltételi függvények deriváltvektorai lineárisan összefüggenek. Nem egy tankönyvet láttam már, ahol ez utóbbi eshetőséget elfelejtették a példamegoldások során külön megvizsgálni (és így bizonyos, erre kihegyezett példákat nem is jól oldanának meg). A mi esetünkben ez az eset azért nem fordulhat elő, mert ahol lineáris függőség van, azok a pontok nincsenek a hipergömb felületén.
Aztán a másik apróság, hogy azt mondtuk: az xi-k egy másodfokú egyenlet megoldásai. Azonban a másodfokú egyenlet csak elsőfokú, ha az egyik multiplikátor éppen nulla lenne. Ekkor minden xi azonos lenne, de ez is ellentmondást adna a feltételi egyenletekkel.]
|
| Előzmény: [305] Lóczi Lajos, 2005-11-20 18:37:23 |
|
| [305] Lóczi Lajos | 2005-11-20 18:37:23 |
 Na igen, kétféle értéket vehetnek fel az xi-k, ez igaz, az egyik értéket vegye fel k darab, a másik értéket (n-k) db (k=1,2,3,...,n-1; mind egyforma nem lehet, ezt könnyű látni). Ezeket behelyettesítve a két eredeti feltételi egyenletünkbe (t.i. az xi pontok a hipergömbfelületen és a hipersíkon is rajta vannak) megkapjuk, mi is lehet az a kétféle érték, ez az amit Te u-val és v-vel jelöltél.
Azonban u és v is függ k-tól! Tehát az Általad leírt egyenlőtlenséglánc egyáltalán nem látszik, és ez az a pont, ahol nekem is csak numerikus kísérleteim vannak.
|
| Előzmény: [304] nadorp, 2005-11-20 17:31:44 |
|
| [304] nadorp | 2005-11-20 17:31:44 |
 Hülyeséget írtam, nem xi= xj , hanem arra gondoltam, amire Te,hogy ebből némi esetszétválasztással kétféle érték adódhat az xikre. A vége változatlan. xj , hanem arra gondoltam, amire Te,hogy ebből némi esetszétválasztással kétféle érték adódhat az xikre. A vége változatlan.
|
| Előzmény: [303] nadorp, 2005-11-20 17:17:53 |
|
| [303] nadorp | 2005-11-20 17:17:53 |
 Én ezt csináltam,de találtam valamit. Ha a Lagrange multiplikátor módszerrel dolgozol, akkor pld:
x1x2..xn-1=2axn+b. Mivel xn>0,ezért szorozhatunk vele
x1...xn=2axn2+bxn, azaz
2axi2+bxi=2axj2+bxj, amiből következik, hogy xi= xj. Tehát a számok csak kétféle értéket vehetnek fel.Legyen ez a két érték u és v. Ekkor ha pld. u>v, akkor xj. Tehát a számok csak kétféle értéket vehetnek fel.Legyen ez a két érték u és v. Ekkor ha pld. u>v, akkor
uvn-1<u2vn-2<u3vn-3<...<un-1v miatt szélsőérték csak ott lehet, ahol az egyik szám egyszer, másik (n-1)-szer szerepel.
|
| Előzmény: [302] Lóczi Lajos, 2005-11-20 15:25:56 |
|
| [302] Lóczi Lajos | 2005-11-20 15:25:56 |
 A pontosság kedvéért hozzá kell tennem, hogy az én bizonyításom sajnos nem teljes.
Lagrange-multiplikátorokkal némi meggondolás (és esetszétválasztás) után kiadódnak azok a pontok, ahol a szorzatnak szélsőértéke lehet: k db xi azonos az 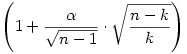 számmal és (n-k) db azonos az számmal és (n-k) db azonos az 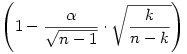 értékkel, ahol k=1,2,...,n-1. értékkel, ahol k=1,2,...,n-1.
A gömb azonban kompakt és a függvény folytonos, ezért létezik minimum és maximum, tehát a fenti pontok között ott van a szorzat minimuma és maximuma.
A numerikus kísérletek szerint k=1-nél lesz a maximum, és k=n-1-nél a minimum, de ezt nem tudtam pár óra alatt belátni (több időt pedig nem tudok rászánni egyelőre). Elég lenne bebizonyítani, hogy a
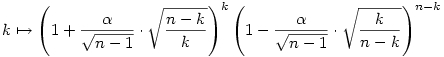
függvény monoton fogyó a lehetséges k értékekre, a lehetséges n és  paraméterértékek mellett, de ez így nem tűnik egyszerűnek. paraméterértékek mellett, de ez így nem tűnik egyszerűnek.
Te milyen módszerrel jutottál túl ezen a ponton (ha egyáltalán ilyesféleképp csináltad)?
|
| Előzmény: [301] nadorp, 2005-11-20 13:34:19 |
|
|
| [300] Lóczi Lajos | 2005-11-19 20:27:52 |
 Nyilván csak 0< <1 vizsgálata szükséges. <1 vizsgálata szükséges.
Láttuk, hogy  =1 esetén valamelyik xi-nek 0-nak kell lennie, hogy a szorzat minimális legyen. Az is leolvasható az adott bizonyításból, hogy ha =1 esetén valamelyik xi-nek 0-nak kell lennie, hogy a szorzat minimális legyen. Az is leolvasható az adott bizonyításból, hogy ha  >0, akkor minden xi>0 kell legyen, hogy a gömbfelületen maradjunk. >0, akkor minden xi>0 kell legyen, hogy a gömbfelületen maradjunk.
A megoldás a 61. feladatra az lesz, hogy az adott gömbfelületen elhelyezkedő xi számok (i=1,2,...,n) szorzata pontosan akkor minimális, ha közülük valamely (n-1) db egyenlő az 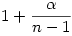 számmal, továbbá 1 darab közülük egyenlő (1- számmal, továbbá 1 darab közülük egyenlő (1- )-val. A minimum értéke ebből már meghatározható. )-val. A minimum értéke ebből már meghatározható.
Másrészt, ez ugyan nem volt kérdés, de az xi számok (i=1,2,...,n) szorzata pontosan akkor maximális, ha közülük valamely (n-1) db egyenlő az 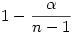 számmal, továbbá 1 darab egyenlő (1+ számmal, továbbá 1 darab egyenlő (1+ )-val. )-val.
|
| Előzmény: [299] Róbert Gida, 2005-11-18 15:54:44 |
|
|
| [298] nadorp | 2005-11-18 09:19:59 |
 a) Legyen e1=(n,0,0,...,0),e2=(0,n,0,...,0)...,en=(0,0,...,n). Ekkor az ei pontok nyilván egy szabályos (n-1) dimenziós S szimplexet határoznak meg. Ha x=(x1,x2,...,xn) eleme ennek a szimplexnek, akkor
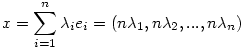 , ahol , ahol 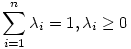 , azaz , azaz 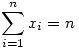 és xi és xi 0. Fordítva, ha 0. Fordítva, ha
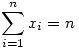 ,xi ,xi 0, akkor 0, akkor 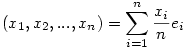 és itt és itt 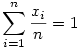 , azaz x eleme S-nek. Tehát a megoldáshalmaz egybeesik S-sel. , azaz x eleme S-nek. Tehát a megoldáshalmaz egybeesik S-sel.
b) Ha s a súlypont, akkor 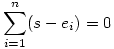 , azaz, , azaz, 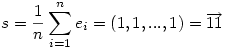
c)Az n-dimenziós térben egy (n-1) dimenziós gömböt úgy kaphatunk,ha egy n-dimenziós gömböt elmetszünk egy (n-1) dimenzós síkkal. Ha P=(p1,p2,...,pn) a beírt gömb sugara, akkor szükségképpen S síkjában helyezkedik el,azaz 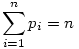 . Határozzuk meg P távolságát a szimplex (n-2) dimenziós lapjaitól, vegyük pld. a . Határozzuk meg P távolságát a szimplex (n-2) dimenziós lapjaitól, vegyük pld. a 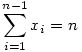 lapot. Ekkor a (p1,...,pn-1,0) pontnak a laptól való távolsága lapot. Ekkor a (p1,...,pn-1,0) pontnak a laptól való távolsága 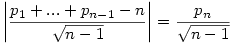 . Tehát P távolsága a laptól . Tehát P távolsága a laptól 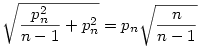 . Ezt elvégezve az összes többi (n-2) dimenziós lapra és felhasználva, hogy ezek a távolságok egyenlőek kapjuk, hogy p1=p2=...=pn=1, azaz . Ezt elvégezve az összes többi (n-2) dimenziós lapra és felhasználva, hogy ezek a távolságok egyenlőek kapjuk, hogy p1=p2=...=pn=1, azaz  és a beírt gömb sugara és a beírt gömb sugara 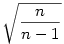
d) Nyilván, ha xi=0, akkor a szorzat 0, azaz minimális lehet.Megmutatjuk, hogy vannak ilyen pontok. Azt kell belátni, hogy pld. létezik x=(x1,x2,...,xn-1,0) pont úgy, hogy
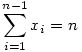 , xn=0 és , xn=0 és
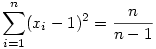 . .
A második egyenlőséget átrendezve felhasználva az elsőt:
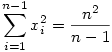 . Tehát . Tehát
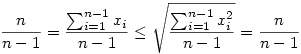 . Egyenlőség van, azaz . Egyenlőség van, azaz 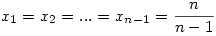 . Hasonlóan kapjuk a többi n-1 darab pontot is. . Hasonlóan kapjuk a többi n-1 darab pontot is.
|
| Előzmény: [296] Róbert Gida, 2005-11-16 22:17:53 |
|
| [297] Róbert Gida | 2005-11-16 23:30:48 |
 60. feladat
Bizonyítsuk be vagy cáfoljuk meg:
A szabályos 30-szög belsejében pontosan 331 darab különböző olyan pont van, amin legalább 5 átló megy át.
|
|
| [296] Róbert Gida | 2005-11-16 22:17:53 |
 59. feladat
Legyen 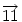 az n dimenziós csupa 1 oszlopvektor. S legyen az az n dimenziós csupa 1 oszlopvektor. S legyen az 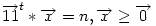 megoldáshalmaza. Bizonyítsuk be, hogy: megoldáshalmaza. Bizonyítsuk be, hogy:
a: Az S egy szabályos (n-1) dimenziós szimplex
b: Mi az S súlypontja?
c: Mi az S-be írható (n-1) dimenziós gömb középpontja és sugara?
d: Mennyi 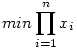 ahol x=(x1,x2,...,xn) a beírható gömb felszínén van. A minimumot mely pontokban veszi fel? ahol x=(x1,x2,...,xn) a beírható gömb felszínén van. A minimumot mely pontokban veszi fel?
|
|
|
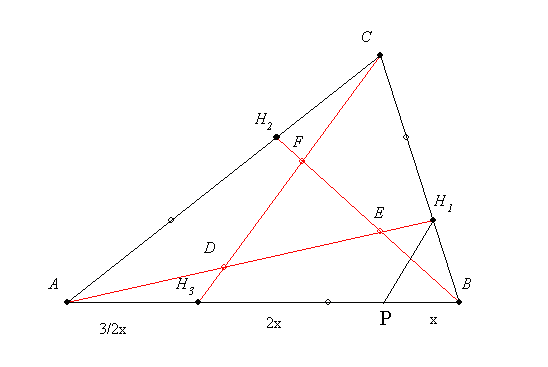
| [294] nadorp | 2005-11-15 15:01:25 |
 Jelentkező hiányában megróbálom. Húzzunk párhuzamost H1-ből CH3-mmal, ez az AB oldalt P-ben metszi.Ekkor ha PB=x, akkor a párhuzamos szelők tétele szerint H3P=2x és mivel H3 harmadoló pont, 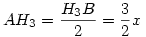 . Az . Az 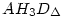 és és 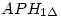 háromszögek hasonlóak, a hasonlóság aránya az előbbiek szerint háromszögek hasonlóak, a hasonlóság aránya az előbbiek szerint 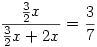 , így az AH3 és AP oldalakhoz tartozó magasságok aránya is ennyi.Ha m jelöli az AP-hez tarozó magasságot, akkor azt kaptuk, hogy , így az AH3 és AP oldalakhoz tartozó magasságok aránya is ennyi.Ha m jelöli az AP-hez tarozó magasságot, akkor azt kaptuk, hogy
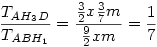 , azaz ha T jelöli az ABC háromszög területét, akkor , azaz ha T jelöli az ABC háromszög területét, akkor 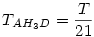 . Hasonlóan ugyanez igaz a másik két kis háromszögre is. Másrészt ennek alapján . Hasonlóan ugyanez igaz a másik két kis háromszögre is. Másrészt ennek alapján 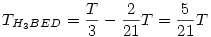 és ugyanez igaz a másik két keletkező négyszögre is. Összefoglalva és ugyanez igaz a másik két keletkező négyszögre is. Összefoglalva

|
 |
| Előzmény: [290] lorantfy, 2005-11-12 22:07:51 |
|
|
|
| [291] BohnerGéza | 2005-11-14 23:12:30 |
 58. feladat:
Az ABC háromszög beírt körének érintési pontjai A', B' és C', középpontja O, K az A'B'C' körülírt körének kp-ja.
Jelölje Ma az AC'B', Mb a BA'C' és Mc a CB'A' háromszög magasságpontját, valamint M az MaMbMc háromszög magasságpontját.
Legyen Oa az AC'B', Ob a BA'C' és Oc a CB'A' háromszög beírt körének középpontja, és K' az OaObOc körülírt körének kp-ja.
Bizonyítandó, hogy az O, a K, az M és a K' egybeesnek!
|
|
|
| [289] lorantfy | 2005-11-08 22:14:48 |
 A komplex számos megoldást itt a Fórumon is megtalálhatod a Felmerülő kérdések... témában Sirpi [143] hozzászólása. Ahogy az a megoldás, ez sem használja fel, hogy a szabályos háromszögek nem közös csúcsai egy körön vannak. Tehát elegendő annyit feltenni, hogy van egy közös csúcsuk.
|
 |
| Előzmény: [288] AzO, 2005-11-08 17:38:22 |
|
| [288] AzO | 2005-11-08 17:38:22 |
 Mostanaban kaptuk ezt a mackosajtos feladatot algebran, es komplex szamokkal (egyseggyokokkel) oldottuk meg, es mondta a tanar, hogy nem is akar belegondolni milyen nehez lenne elemi (kozepiskolai) modszerekkel megoldani :). Ennek ellenere ez frappans volt, es sztem megmutatom neki :) Koszi
|
| Előzmény: [287] lorantfy, 2005-11-06 12:04:50 |
|
| [287] lorantfy | 2005-11-06 12:04:50 |
 Tomszy feladata a Felmerülő kérdések ... témából:
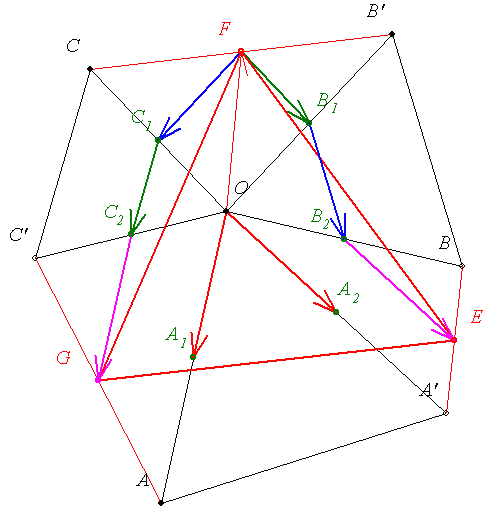
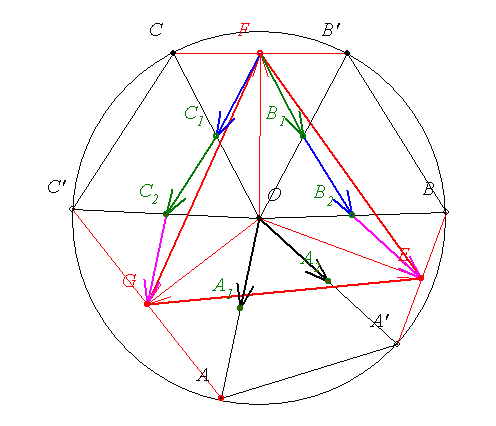
Egy r sugarú körben vegyünk fel három r sugarú húrt: AA', BB', CC'. Jelöljük A'B húr felezőpontját E-vel, B'C húr felezőpontját F-vel és C'A húr felezőpontját G-vel.
Bbh. EFG háromszög szabályos!
Megoldás vektorokkal: (Ugyanúgy megy mint a B.3837. feladat megoldása, amit a Lejárt határidejű ... témába írtam be.)
Legyenek A1,A2,B1,B2,C1,C2 a megfelelő, sugás hosszúságú szakaszok felezőpontjai.
A háromszög középvonalának tulajdonságai és a szabályos háromszögek miatt az ábrán azonos színnel jelölt vektorok egymásnak 60 fokos elforgatottjai.

Mivel a megfelelő összetevő vektorok egymás 60 fokos elforgatottjai, így 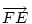 is 60 fokos elforgatottja is 60 fokos elforgatottja 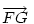 -nek, tehát EFG -nek, tehát EFG szabályos háromszög. szabályos háromszög.
|
 |
|
|
| [285] Lóczi Lajos | 2005-09-20 13:59:13 |
 Jó, de nézd meg, hogy mi a könyv célja: könnyítést adni azoknak, akiknek nehezen megy, bizonyos területekre így kevesebb előismerettel is el lehet jutni -- persze onnan nem lehet olyan messzire továbbhaladni.
(Az elvi célja pedig inkább az, ahogy írja, hogy közben a geometriát nem kell a valós számok bonyolult fogalmára építeni: tetszőleges algebrai test is használható.)
|
| Előzmény: [284] Fálesz Mihály, 2005-09-20 11:35:29 |
|
| [284] Fálesz Mihály | 2005-09-20 11:35:29 |
 Én nem lelkesedek érte, sőt.
Trigonometria-feladatokban a szögeknek legfeljebb csak a szinuszát/koszinuszát szoktuk kiszámolni, magukat a szögeket nem. Négyzetgyökökkel pedig így is, úgy is számolni kell. Például elég megkérdezni, hogy ha az A,B,C pontok egy egyenesen vannak, mondjuk AB2=2 és BC2=3, akkor mekkora lehet AC2. A konstrukció csak a legegyszerűbb esetekben teszi félre a négyzetgyökvonást, a számolás egyáltalán nem lesz tőle sem könnyebb, sem egyszerűbb.
A trigonometrikus függvények elvetését pedig kb. olyan ötletnek tartom, mint ha valaki a prímszámtételből ki akarná irtani a logaritmust (mert hát ugye mi szükség van transzcendens függvényekre, ha egész számokról akarunk beszélni), vagy a Cardano-képletből a komplex számokat. Pont a matematikát akarja kiirtani; azt, hogy hozzunk létre elméleteket, új objektumokat (jelen esetben a trigonometrikus függvényeket), amik megmutatják, hogy a dolgok mögött milyen mélyebb összefüggések vannak.
F.M.
|
| Előzmény: [282] Lóczi Lajos, 2005-09-19 22:50:10 |
|
| [282] Lóczi Lajos | 2005-09-19 22:50:10 |
 Szép és elegáns a leírás, sokmindenben egyetértek vele, bár nem hiszem, hogy túlzottan nagy változást okozna mifelénk belátható időn belül, ha egy olyan alapvető fogalomhoz, mint a "szög" akar hozzányúlni, átdefiniálni.
|
| Előzmény: [281] 2501, 2005-09-19 10:25:15 |
|
|
|
| [280] Szalkai István | 2005-09-14 13:42:39 |
 Kedves Mindenki !
A 2005.jan. feladatot általánosítva jutott eszembe a a következő probléma: Mi azon pontok mértani helye, amelyeknek adott egyenesektől való távolságai kielégítenek egy lineáris összefüggést? "Felfedezésem" biztosan nem új, bár irodalomban nem akadtam a nyomára. Közzéteszem mégis, hátha esetleg valakinek hasznára válik, no és biztosan én is tanulok hozzászólásaitokból! (Más fajta TEX-et használva nem sikerült a szöveget ide feltennem, de a következő linken megtalálható:
http://www.szt.vein.hu/~szalkai/Tavolsagok-jav.pdf
Üdvözlettel: szalkai@almos.vein.hu
|
|
| [279] BohnerGéza | 2005-08-27 00:19:34 |
 Jogos [275] jonas észrevétele, bár csak egy kis fogalmazási hibát követtem el. A zárójel szövege helyesen: valamint a talpponti háromszög területének. Igaz ez már nem nehéz, ha az előzőekre megvan a válasz.
|
| Előzmény: [275] jonas, 2005-08-23 22:40:10 |
|
| [278] lorantfy | 2005-08-24 10:25:21 |
 Hello Viktor!
Ez az EUKLIDES program. A 2.02 verzió ingyenesen letölthető: www.euklides.hu.
Töltsd le és szórakozz el vele. Én a kész ábrát Print Screen-el vágólapra szoktam tenni. Aztán egy képszerkesztővek kivágom a lényeges részt és átlátszóvá teszem, majd elmentem gif-ben és úgy csatolom a hozzászóláshoz. Így a háttérszínen jelenik meg.
|
| Előzmény: [277] xviktor, 2005-08-24 10:09:36 |
|
|
|
|
| [274] BohnerGéza | 2005-08-23 22:08:14 |
 Üdv mindenkinek!
Köszönöm Kós Ritának [273] a segítséget!
57. (számozott) feladat: Egy háromszög oldalai 13, 14 és 15. Adjuk meg a pontos értékét a
a.) beírt köre sugarának
b.) TcBTa (Ta és Tc magasságtalppontok) beírt köre sugarának
c.) TcBTa háromszög területének ( a talpponti háromszög területének )
|
|
| [273] Kós Rita | 2005-07-26 19:31:42 |
 A lekepezesek szorzatarol rovidebben-hosszabban Reiman Istvan konyveiben is van szo: Fejezetek az elemi geometriabol (Typotex, pici vekony, ebben biztosan), ill. A geometria es hatarteruletei c. konyvben, ha jol emlekszem.
|
| Előzmény: [272] BohnerGéza, 2005-07-15 23:09:11 |
|
| [272] BohnerGéza | 2005-07-15 23:09:11 |
 Az 50., 51., 53. és 56. feladat közös, általános megoldása.
Igen örülök lorantfy és Kós Géza 56. feladatra a [267]-ben ill. [268]-ban leírt megoldásának. Ezek is alkalmasak az általánosításra.
Ha valaki még nem ismeri a leképezések szorzatát, annak is megérthető amit írok, de időt és energiát kell rá szánnia, végigjátszva-gondolva minden állítást!
A téma bővebb megismeréséhez Rácz János könyveit tudom ajánlani, de ezek nehezen érhetők el. Rossz memóriám miatt további könyveket most nem tudok, remélem lesz valaki és kisegít!
Jelölje az A körüli alfa forgatást (A|alfa). Legyen
(1)...(C|gamma)*(B|béta)*(A|alfa)=I helybenhagyás.
//A leképezések szorzatát - egymás utáni elvégzését - visszafelé olvasva kell értelmezni, tehát először A, majd B, végül C körül forgatunk,// Helybenhagyást akkor kapunk, ha összesen n*360 fokot, ahol n egész, forgatunk és van fixpont. Ez a fent jelzett feladatok esetén áll. Az egyszerűség kedvéért és mert ilyen esetre ezen feladatok mindig visszavazethetők n=1 (vagy -1) esettel foglalkozunk.
Tudnunk kell még, hogy egy forgatás helyettesíthető két tengelyes tükrözés szorzatával, pl. (A-alfa)=t2*t1, ahol t1 és t2 is átmegy A-n, valamint t1 és t2 szöge alfa fele az irányítást is figyelembe véve. (1)-et balról (C|-gamma)-val szorozva:
(2)...(B|béta)*(A|alfa)= (C|-gamma)
Legyen t2=AB, t1 és t3 pedig olyan egyenesek, melyekre (A|alfa)=t2*t1 és (B|béta)=t3*t2. Ekkor
(3)...(B|béta)*(A|alfa)=(t3*t2)*(t2*t1)=t3*(t2*t2)*t1=t3*t1= (C|-gamma)
Tehát t1 és t3 is átmegy C-n. Mindent végiggondolva ABC olyan háromszög kell legyen, melyben a megfelelő csúcsoknál alfa/2, béta/2 ill. gamma/2 szög van. //Feltéve, hogy egyik szög sem n*360 fok, azaz mind a három forgatás valódi fogatás. //
Jó munkát a fent jelzett feladatok átgondolásához! Kitalálható esetleg újabb konkrét feladat is?!
|
| Előzmény: [268] Kós Géza, 2005-07-11 12:00:08 |
|
| [271] Hajba Károly | 2005-07-11 16:43:28 |
 Köszi a továbbképzés. Tényleg egyszerű.
De talán már nem olyan egyszerű azon zárt görbe megszerkesztése, mely görbe bármely pontjára azonos a PA+PB+PC hossz nagysága. Ezen görbe elfajult esete az I pont is.
HK
|
| Előzmény: [270] lorantfy, 2005-07-11 15:40:54 |
|
| [270] lorantfy | 2005-07-11 15:40:54 |
 Kedves Károly!
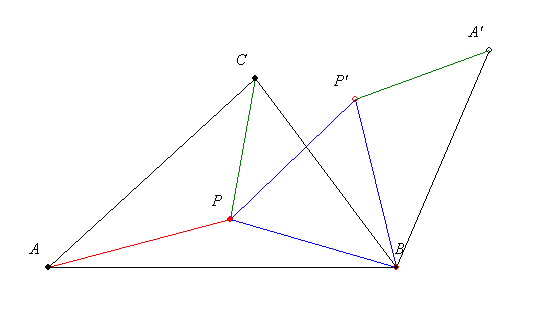
A tétel igaz: Ha az ABC hegyesszögű háromszög síkjában lévő P pontra igaz, hogy AP+BP+CP összeg minimális, akkor P a háromszög izogonális pontja (melyből mindhárom oldal 120 fokos szögben látszik.)
A bizonyítás nagyon szép és egyszerű. Forgassuk el a B pont körül a BCP háromszöget 60 fokkal. Mivel BP'P háromszög egyenlő oldalú, ezért az APP'A' törött vonal hossza megegyezik az AP+BP+CP összeggel. Az A' helyzete P-től független. APP'A' hossza akkor minimális, ha P és P' az AA' egyenesre illeszkedik. Ez pedig akkor van, ha APB és BPC és BPC 120o, vagyis ha P az izogonális pont. 120o, vagyis ha P az izogonális pont.
|
 |
| Előzmény: [269] Hajba Károly, 2005-07-11 13:31:23 |
|
| [269] Hajba Károly | 2005-07-11 13:31:23 |
 Üdv!
Érdekesnek tűnik a háromszög I pontja más szempontból is, mintha erre a pontra igaz, hogy PA + PB + PC hossz a legrövidebb, ahol A, B, C a háromszög csúcsai, míg P egy tetszőleges pont a síkjukban. Bizonyítani nem tudom, csak ráleltem. Ha igaz, gondolom egy -általam nem- ismert tétel.
Egy adtok egy kis továbbképzést vagy címeket, megköszönném. :o)
O.
|
| Előzmény: [268] Kós Géza, 2005-07-11 12:00:08 |
|
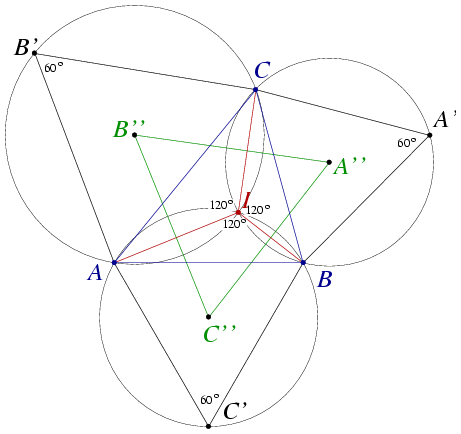
| [268] Kós Géza | 2005-07-11 12:00:08 |
 Legyen az AC'B és BA'C köré írt körök B-től különböző metszéspontja I. Az AC'BI és BA'CI húrnégyszögek szögeiből AC'B =BA'C =BA'C =120o. Ebből következik, hogy CB'A =120o. Ebből következik, hogy CB'A =120o, vagyis az I pont a CB'A körön is rajta van. =120o, vagyis az I pont a CB'A körön is rajta van.
Ha az ABC háromszög mindegyik szöge 120 foknál kisebb, akkor I a háromszög izogonális pontja. Ha valamelyik szög éppen 120 fok vagy annál nagyobb, akkor nincs izogonális pont, és az ábra kicsit máshogy néz ki, de a három kör akkor is egy ponton megy át.
Az IA'', IB'', IC'' szakaszok (egyenesek) páronként 120 fokos (60 fokos) szöget zárnak be. Az A''B'', B''C'', C''A'' egyenesek két-két kör centrálisai, amik merőlegesen felezik az IA'', IB'', IC'' közös húrokat. Ezek az egyenesek tehát szintén páronként 60 fokos szöget zárnak be egymással.
|
 |
| Előzmény: [267] lorantfy, 2005-07-10 17:00:12 |
|
| [267] lorantfy | 2005-07-10 17:00:12 |
 Nem szeretném, ha Géza szép feladata feledésbe merülne!
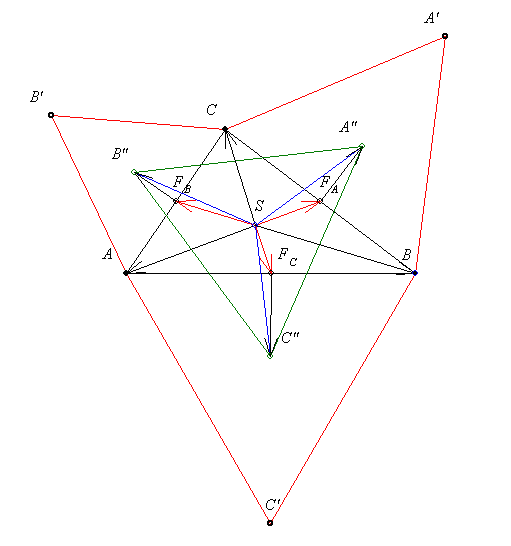
56. feladat megoldása: Helyezzük a koord.rsz. origóját a háromszög S súlypontjába.
Legyen
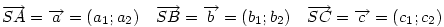
Fejezzük ki 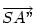 vektort ezek segítségével! vektort ezek segítségével!
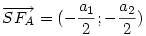
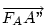 pedig pedig 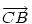 90 fokos, pozitív irányú elforgatottjának 90 fokos, pozitív irányú elforgatottjának 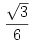 -szorosa. -szorosa.
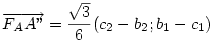
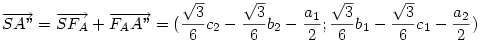
Hasonlóan:
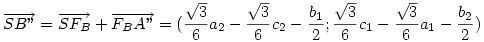
Az origó körüli 120 fokos, pozitív irányú forgatás mátrixa:
![\left[\matrix{cos 120^\circ &sin 120^\circ \cr -sin 120^\circ & cos 120^\circ \cr}\right]=
\left[\matrix{-\frac{1}{2}&\frac{\sqrt3}{2}\cr\frac{-\sqrt3}{2} &-\frac{1}{2} \cr}\right]](keplet.cgi?k=231A6CD88033A9CB)
Ezzel beszorozva 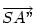 -t és felhasználva, hogy a,b,c vektorok összege 0, vagyis a koordinátákra is: -t és felhasználva, hogy a,b,c vektorok összege 0, vagyis a koordinátákra is:
a1+b1+c1=0, a2+b2+c2=0
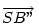 -t kapjuk. Tehát igaza van Dánielnek (=tudniakarok): valóban egyenlő oldalú háromszöget kapunk. -t kapjuk. Tehát igaza van Dánielnek (=tudniakarok): valóban egyenlő oldalú háromszöget kapunk.
|
 |
|
|
| [265] papi | 2005-07-06 08:54:13 |
 Bocsánat ! Természetesen az előbb Torricelli pontot akartam írni (papi)
|
|
| [264] papi | 2005-07-06 08:37:07 |
 Kedves Barátaim ! A h-szög nevezetes pontjainak a köré írható körre vonatkozó hatványait keresgélem. A S-pont, M-pont, beírt kör Kpontja és a Lamoine-féle pont esetében már rájöttem e hetványokra. De a Tossicelli-pontnál elakadtam. Tud valaki segíteni? (papi)
|
|
| [263] Lóczi Lajos | 2005-07-04 23:46:42 |
 Csak kiegészítésképpen írom, hogy a "négyzetes közelítés" az idézett Newton-módszerben persze nem azt jelenti, hogy a szereplő deriváltpolinom épp másodfokú, hanem azt, ahogyan a hiba nagysága csökken: a numerikus módszerek elméletéből ismert, hogy a Newton-módszer gyorsan konvergál, ha megfelelően közelről indítjuk a tényleges megoldástól (azaz z0-t "elég közel" választjuk meg a keresett értékhez, ami jelen esetben z0=1 mellett jó, de általában a pontos vonzási tartomány fraktálbonyolultságú alakzatokból áll, l. pl. http://mathworld.wolfram.com/NewtonsMethod.html)
A konvergencia a jelen esetben olyan gyors, hogy |z3-cos (10o)| 2.10-7, majd |z4-cos (10o)| 2.10-7, majd |z4-cos (10o)| 3.10-14, aztán |z5-cos (10o)| 3.10-14, aztán |z5-cos (10o)| 7.10-28, stb. 7.10-28, stb.
(A hatványsoros közelítés előnye, hogy a kezdeti értékkel nem kell bajlódni, de a konvergencia nem ennyire gyors: az n. lépésben a hiba ott n faktoriálissal arányos.)
|
| Előzmény: [261] jonas, 2005-07-02 10:28:45 |
|
|
| [261] jonas | 2005-07-02 10:28:45 |
 Az igaz, hogy a koszinusz (illetve a hatványsorba fejtése) többet mond az értékről, mint a komplex köbgyökös kifejtés.
Ennek ellenére a harmadfokú egyenlettel is lehet valamit kezdeni, ha már nadorp kiszámolta. Persze ha a megoldóképletet alkalmazzuk rá, akkor sinust kell számolni, de megoldhatjuk közvetlenül a harmadfokú egyenletet valamilyen közelítéssel. Nem nehéz négyzetes közelítést kapni:
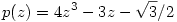
p'(z)=12z2-3
z0=1
zn+1=zn-p(z)/p'(z)
Ekkor zn cos (10deg)=0.98481 cos (10deg)=0.98481
|
| Előzmény: [256] Lóczi Lajos, 2005-06-29 20:38:19 |
|
| [260] Lóczi Lajos | 2005-06-30 10:50:02 |
 Rosszul emlékeztem, nem "tétel"-t, hanem "vizsgakérdés"-t említett. De ez már filozófia. Attól függ, milyen kontextusban van szükség a válaszra. Numerikus matematikai szempontból a táblázat tökéletes, de elméleti szempontból nem mindig.
|
| Előzmény: [259] Lóczi Lajos, 2005-06-30 10:43:26 |
|
| [259] Lóczi Lajos | 2005-06-30 10:43:26 |
 Én is ugyanazt mondtam, mint az első 2 bekezdésed, viszont pontosan megadtam, melyik értékre kell gondolni, tehát nem értem a problémát. És ez nem a megoldóképlet baja, hanem a köbgyöké, mint jelölésé, hiszen a komplex köbgyök nem is függvény. A valós négyzetgyök  -os megállapodásához hasonló megállapodást persze lehet tenni (és pl. a számítógépes programcsomagokban mindig van is ilyen), hogy a "köbgyök-jel" például mindig a (0 és 2 -os megállapodásához hasonló megállapodást persze lehet tenni (és pl. a számítógépes programcsomagokban mindig van is ilyen), hogy a "köbgyök-jel" például mindig a (0 és 2 közé eső) legkisebb irányszögű komplex számok jelentse, és akkor már nincs semmi gond a megoldóképletekkel. közé eső) legkisebb irányszögű komplex számok jelentse, és akkor már nincs semmi gond a megoldóképletekkel.
Viszont az, hogy kikeresel valamit egy táblázatból, szerintem sosem helyes válasz egy matematikai kérdésre, mert nem konstruktív és nem mutat rá a miértre, pláne nem bizonyítás (az eredeti kérdésben "tételt" említett a hozzászóló).
|
| Előzmény: [258] Fálesz Mihály, 2005-06-30 07:03:33 |
|
| [258] Fálesz Mihály | 2005-06-30 07:03:33 |
 A megoldóképlettel az is baj, hogy például az Általad felírt alak a gyököket az 50o+k.120o és a 100o+k.240o szögfüggvényeivel fejezi ki.
Szóval nem jutottunk közelebb, de most már 9, ugyanannyira felírhatatlan szám közül kell kiválasztani a 3 gyököt, amik közül csak az egyik sin 260o, a másik kettő hamis gyök...
Szerintem a helyes válasz az lett volna, hogy (a Függvénytáblából kiolvasva)
sin 260o=sin (180o+80o)=-sin 80o -0,9848. -0,9848.
|
| Előzmény: [256] Lóczi Lajos, 2005-06-29 20:38:19 |
|
| [257] Lóczi Lajos | 2005-06-29 20:44:07 |
 Persze korrekt válasz az is, ha a szinusz-értéket kifejezed a megfelelő oldalhosszú és szögű derékszögű háromszögben a megfelelő oldalak arányával.
És még végtelen sok korrekt válasz létezik, amely sin (260o) értékét más matematikai dolgokhoz, objektumokhoz kapcsolja.
|
| Előzmény: [254] Stegi, 2005-06-28 18:50:34 |
|
| [256] Lóczi Lajos | 2005-06-29 20:38:19 |
 A harmadfokú egyenlet itt sajnos épp olyan, hogy minden gyöke valós, de a megoldóképletében a komplex számok nem kerülhetők ki. (Ez a középkor óta már sokakat idegesített :-)
A három megoldás közül a minket érdeklő most ez:
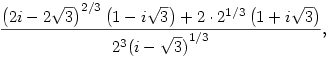
ahol i a komplex képzetes egység és a köbgyökök három lehetséges értéke közül ügyesen kell megválasztani a megfelelőt: a nevezőben szereplő komplex szám 1/3-ik hatványa az a komplex szám, melynek irányszöge 5 /18, nagysága 21/3, a számlálóban szereplő komplex szám 2/3-ik hatványa pedig az a komplex szám, melynek irányszöge 5 /18, nagysága 21/3, a számlálóban szereplő komplex szám 2/3-ik hatványa pedig az a komplex szám, melynek irányszöge 5 /9, nagysága pedig 2.21/3 -- ahol természetesen 21/3 a "közönséges" valós köbgyök. /9, nagysága pedig 2.21/3 -- ahol természetesen 21/3 a "közönséges" valós köbgyök.
Ez tehát -sin (260o) értéke. A fentiekből látszik, hogy ha ilyen formában, algebrai úton válaszolom meg a kérdést, akkor tulajdonképpen semmilyen "kezelhető", "kézzelfogható" információt nem mondtam a keresett szinusz-értékkel kapcsolatban. "A formula szép, de semmire sem jó."
Ellenben itt egy sokkal szebb és hasznosabb formula, az analízis nyelvén:
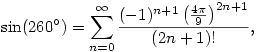
amiből tetszőleges pontossággal ki is lehet számolni a szinusz értékét.
|
| Előzmény: [255] nadorp, 2005-06-29 16:01:16 |
|
| [255] nadorp | 2005-06-29 16:01:16 |
 sin 260o=-sin 80o=-cos10o.
Ismert, hogy cos 3 =4cos3 =4cos3 -3cos -3cos  ,azaz ,azaz
cos30o=4cos310o-3cos 10o
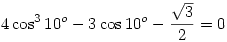
Ez egy harmadfokú egyenlet cos10-re, ami megoldható megoldóképlettel ( ezt már nem írnám le). Szerintem a feladatra ez a korrekt válasz, de nem tudom, hogy a harmadfokú egyenlet tananyag-e ott, ahol tanulsz. Ha középiskolás vagy, akkor úgy tudom nem, ha máshová jársz, akkor attól tartok igen.
|
| Előzmény: [254] Stegi, 2005-06-28 18:50:34 |
|
| [254] Stegi | 2005-06-28 18:50:34 |
 Sziasztok!
Nagyon egyszerű, mégsem tudom. Kérek segítséget. Ez egy vizsgakérdés : "Mennyi sin 260fok?" Mi rá a korrekt válasz?
Köszönom a segítséget.
|
|
|
|
| [251] Doom | 2005-06-10 16:07:35 |
 Köszönöm mindenkinek a sok megoldást! Fálesz 2. megoldása szerintem is nagyon ötletes! :)
|
|
| [250] Fálesz Mihály | 2005-06-10 07:38:40 |
 Sziasztok,
Szerintem próbáljatok meg geometriaibb megoldásokat is kitalálni. Sok mindent ki lehet számolni, de az ilyen megoldások elrejtik a feladatok matematikai szépségeit, a kívülállónak meg azt a hamis képet mutatják, hogy csak ilyen megoldás van.
Érdemes lehet próbálkozni azzal, hogy a C csúcsból invertálunk. (Ez arra jó, hogy harmonikus közepet számtani középre cseréljük.) Utána már semmilyen számolás nem kell, csak egy ügyes segédpont, de ezt már találjátok ki Ti.
Mondanék két alternatív, kicsit számolós, de azért rövid utat is.
1. A szögfelezővektor a két oldalvektor súlyozott átlaga, a súlyokat a szögfelező-tételből megtdhatjuk. Aztán... (Valószínűleg innen jött a feladat is.)
2. Írjuk fel a CAB, CAF és CFB háromszögek területét az a,b,f szakaszokkal és a C-nél levő szögekkel.
Üdv.
F.M.
|
| Előzmény: [249] levi, 2005-06-09 22:41:50 |
|
|
|
| [247] Doom | 2005-06-09 16:21:15 |
 Bizonyítsuk be, hogy egy általános háromszög bármely 'f' szögfelezőjére igaz, hogy ha a vele szemköti oldal 'c', és a msáik kettő 'a' és 'b', akkor 'f' kisebb-egyenlő 'a' és 'b' harmonikus közepénél!
u.i.1: ha vki jól tud ábrát készíteni, nagyon megköszönném, ha csinálna hozzá egyet! :)
u.i.2: c-nem kell a feladat megértéséhez, de nem tudtam ábra nélkül máshogy elmagyarázni :(
|
|
| [246] tudniakarok | 2005-06-08 22:58:15 |
 kritsmének emailben elküldtem még tegnap este a rólad elnevezett Fálesz Mihály tételét,és megfordítását,úgyhogy már nincs rá szüksége,sőt ma a válaszlevelében megköszönte a segítséget,ugyanis 1,7-es átlaggal átment matekból! Ezúton is Grat!
|
| Előzmény: [245] Fálesz Mihály, 2005-06-08 12:35:40 |
|
| [245] Fálesz Mihály | 2005-06-08 12:35:40 |
 Egy másik topikban kritsme szerette volna megtanulni a rólam elnevezett tételt.
A Thálész-tétel azt mondja ki, hogy egy kör átmérője a kör pontjaiból derékszögben látszik (kivéve persze az átmérő két végpontját, ahol baj van az egyik iránnyal), lásd az arcképemet.
A tételnek van megfordítása és egy kicsit erősebb változata is: az átmérő a körvonal pontjaiból derékszögben, a belső pontokból tompaszögben, a külső pontokból hegyesszögben látszik. Mindennek a bizonyítása sem nehéz. Kedves Kritsme! Melyikre van szükséged?
|
|
|
| [243] BohnerGéza | 2005-06-02 18:54:34 |
 56. feladat: Az ABC háromszög oldalaira a CBA', az ACB' és a BAC' azonos körüljárású szabályos háromszöget írtuk. Ezek A", B", C" súlypontja milyen háromszöget határoz meg?
|
|
| [242] BohnerGéza | 2005-06-02 18:48:21 |
 Megjegyzések az 50. és 51. feladathoz.
Az 50. feladattal kapcsolatban Hraskó András hívta fel arra a figyelmemet, hogy tulajdonképpen Pascal-tételre feladat. Teljesen igaz, ajánlom mindenki figyelmébe! Ha valaki kedvet érez hozzá, kérem írja be bővebben ezt a megoldást!
A [239.]-ben leírt megoldásnál a Pascal-tételes általánosabb, nem használja ki, hogy F a PR felezőpontja.
Az 51. feladatot az 50. [239] vázolt megoldás közben tulajdonképpen megoldottuk (, hivatkozva az 53. feladatra). Ha valaki kedvet érez hozzá, kérem írja be ennek a megoldását!
(Még ennyi segítség mellet sem könnyű feladatok!)
|
| Előzmény: [239] BohnerGéza, 2005-05-19 19:03:44 |
|
| [241] Hraskó András | 2005-05-20 21:56:15 |
 Kedves Géza!
Az 55. feladatban kitűzött szerkesztés, azt hiszem, teljes általánosságban nem végezhető el euklideszi módszerekkel.
Ha jól látom, akkor a háromszög a, b, c oldalai és beírt körének r sugara között az
r2s-(s-a)(s-b)(s-c)=0
összefüggés áll fenn (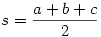 ). Ez c-re nézve (a-t, b-t és r-t tekintjük adottnak) harmadfokú egyenlet. A bal oldali polinom az a, b, r adatok megfelelő választása mellett a racionális számtest felett irreducibilis is, így a szerkeszthetőség elmélete (Galois elmélet) szerint c nem szerkeszthető. ). Ez c-re nézve (a-t, b-t és r-t tekintjük adottnak) harmadfokú egyenlet. A bal oldali polinom az a, b, r adatok megfelelő választása mellett a racionális számtest felett irreducibilis is, így a szerkeszthetőség elmélete (Galois elmélet) szerint c nem szerkeszthető.
|
|
|
| [239] BohnerGéza | 2005-05-19 19:03:44 |
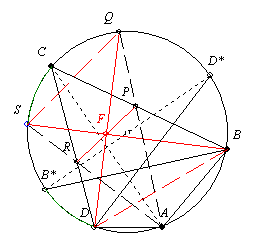
 Az 50. feladat megoldása: Sajnos a [229.] ábráján a csúcsok betűzését elrontottam, így új ábra is készült.
A megoldás vázlatát írom csak le, teret engedve az önálló munkának is.
A megoldás lényege: Legyen F a PR felezőpontja. Megmutatjuk, hogy DBF szög = DBS szöggel = béta felével. Ez elég a feladat állításának igazolásához, hiszen analóg módon igaz, hogy BDF szög = BDQ szöggel.
Az 53. feladatot felhasználva kapjuk, hogy DBF szög a béta fele.
Mivel B*BC szög a béta fele és CS ív=B*D ívvel, ezért DBS szög is a béta fele.
|
 |
| Előzmény: [227] BohnerGéza, 2005-04-14 22:32:17 |
|
|
|
|
| [235] secand | 2005-05-12 21:49:18 |
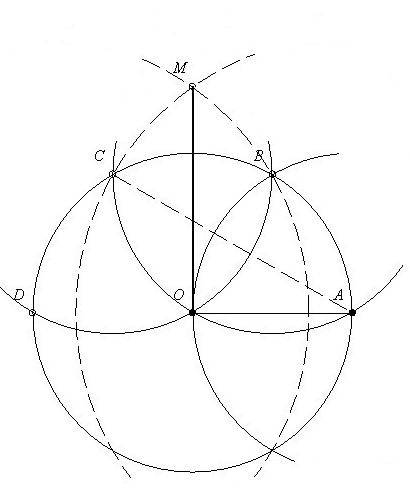
 Megoldás az 52. feladatra:
1.ábra: Az O középpontú kör egy tetszőleges pontjából(:=A) körívezzünk a megadott sugárral a kör kerületére,így kapjuk a B,C,D pontokat!Az AC szakasz a körbe írható szabályos háromszög oldala,ezt körzőnyílásba véve,és körözve A illetve D pontokból metszéspontként kapjuk M pontot!Pit. tétellel belátható hogy az OM szakasz a körbe írható négyzet oldala,így már könnyen oszthaó a kör négy egyenlő ívre,ahonnan már csak néhány,a megadott sugárral való körzés választ el a négy területrésztől...
|
 |
| Előzmény: [228] tudniakarok, 2005-04-20 22:03:19 |
|
| [234] KiCsa | 2005-05-12 15:04:27 |
 55. feleadat: Szerkesszünk háromszöget, ha adott két oldala és a beírt kör sugara!
Bocsánat ha lett volna.
|
|
| [233] joe | 2005-05-10 18:44:56 |
 54. feladat: Legyen k egy félkör O középponttal és AB átmérővel. Legyen M a BA félegyenessel ellentétes félegyenes egy B-től különböző pontja. Az AB-től különböző p egyenes haladjon keresztül az M ponton és messe a k félkört két, egymástól különböző C és D pontban, miközben |MC| > |MD|. Legyen K az AOC és a BOD háromszögek köré írt köreinek O-tól különböző metszéspontja. Bizonyítsuk be, hogy OK merőleges MK-ra.
|
|
| [232] BohnerGergő | 2005-05-05 19:28:02 |
 Kiegészítés az 53. feladat megoldásához:
Az indoklásból kimaradt, hogy a két forgatás szorzata azért egyenlő az F körüli 180 fokos forgatással, mert a két forgatás szögének összege 180 fok.
|
| Előzmény: [231] BohnerGergő, 2005-05-05 19:03:13 |
|
