| [1749] Sinobi | 2013-10-30 20:58:07 |
 Adott a síkon négy pont. Tekintsük az összes kúpszeletet, amelyek áthaladnak ezen a négy ponton. Mi az ilyen tulajdonságú kúpszeletek középpontjának mértani helye?
|
|
|
| [1747] Sinobi | 2013-10-25 11:48:47 |
 Egy M középpontú, k(M) paraméterű ("sugárnégyzetű") inverzió fixen hagyja a k kört (és a t kört is). Ahol k(M) az M pont k-ra vonatozó hatványa.
A szelőtétel értemében minden M-en átmenő szelőre igaz lesz, hogy az egyik metszéspont képe a másik, és a másik metszéspont képe az egyik lesz, tehát k fixen marad.
(ha M k-ra esik, akkor tényleg nem működik, máshogy kell meggondolni.)
|
| Előzmény: [1746] HoA, 2013-10-25 11:15:32 |
|
|
| [1745] Sinobi | 2013-10-12 22:45:10 |
 Az A.595-ös feladat is szépen megoldható majdnem kizárólag az inverzió fogalmait és tételeit használva. Megoldásvázlat:
1: Belátom, hogy AC, EF és GH egy pontban, Y-ban metszik egymást.
1.5: Y polárisa BD
2: tehát EP FQ BD-n helyezkedik el. FQ BD-n helyezkedik el.
1: bizonyítása: Legyen Y:=EF GH. Felveszem az A és C középponttú, AE és CF sugarú köröket. Y-ból egy olyan inverzió, amely k-t fixen hagyja kicseréli ezeket a köröket, tehát a középpontjukat összekötő AC egyenesen Y is rajta van. GH. Felveszem az A és C középponttú, AE és CF sugarú köröket. Y-ból egy olyan inverzió, amely k-t fixen hagyja kicseréli ezeket a köröket, tehát a középpontjukat összekötő AC egyenesen Y is rajta van.
1.5: ez nem inverzióval: Y rajta van B és D polárisán, tehát B és D rajta van Y polárisán.
2: azt fogom belátni, hogy ha Y-ból húzok két szelőt, amiknek a metszései k-val P,Q és E,F, akkor M:=EP FQ Y polárisán helyezkedik el.. FQ Y polárisán helyezkedik el..
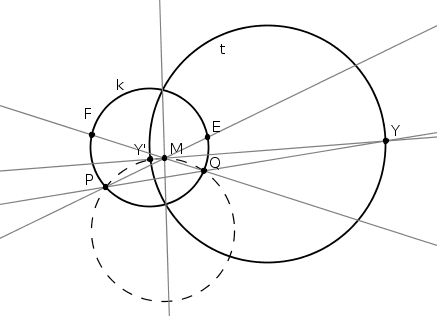
Legyen az Y-ból húzott tetszőleges szelő két metszéspontja k körrel P és Q! Legyen M pont Y polárisának egy tetszőleges pontja! Vegyük fel YO (O k középpontja) Thalészkörét, legyen t. Egy olyan, Y kp-ú inverzió, amely k-t fixen hagyja, t-t Y polárisába viszi. Legyen Y':=YM t. Y' rajta van a PQM körön, mert az Y középponttú inverzió kicseréli M-t és Y'-t, és fixen hagyja a PQM kört. Az M kp-ú, k-t fixen hagyó inverzióra legyen P képe E, és Q képe F. Az inverzió fixen hagyja a t kört is, mert rajta van k és t hatványvonalán, és ha kicseréli k két pontját, akkor t-ét is. Ezért Y' képe Y, tehát PQM kör képe EFY egyenes. t. Y' rajta van a PQM körön, mert az Y középponttú inverzió kicseréli M-t és Y'-t, és fixen hagyja a PQM kört. Az M kp-ú, k-t fixen hagyó inverzióra legyen P képe E, és Q képe F. Az inverzió fixen hagyja a t kört is, mert rajta van k és t hatványvonalán, és ha kicseréli k két pontját, akkor t-ét is. Ezért Y' képe Y, tehát PQM kör képe EFY egyenes.
Ezzel beláttuk, hogy ha Y-ból húzunk egy szelőt (PQY), és felveszünk egy tetszőleges M pontot a polárisán, és vesszük az E:=PM k és F:=QM k és F:=QM k pontokat, akkor EFY egy egyenesbe esnek. k pontokat, akkor EFY egy egyenesbe esnek.
Ebből már következik PQY és EFY szelőkre, mert felvéve M pontot, mint PE és Y polárisának metszését, azt kapjuk, hogy F' egy olyan pont, amire F'EY egy egyenesbe esnek, és F' rajta van k-n, tehát F'=F, és M=EP FQ rajta van Y polárisán, BD-n. FQ rajta van Y polárisán, BD-n.
|
 |
|
| [1744] Sinobi | 2013-09-29 13:54:16 |
 Vagy elsiklottam felette, vagy nem igazoltad. Mindegy. Leölöm most őket, ne csúfoskodjanak itt a megoldásuk nélkül.
[1723]: Ha A és B rögzített, C egy AB-vel párhuzamos egyenesen futhat, mi ABC háromszög magasságpontjának mértani helye?
Tükrözöm az M pontot az AB egyenesre. A, B, C, M' egy körön van, és CM' merőleges AB-ra. Felveszem X pontot, mint CM' és AB metszéspontját. X körhatványa az ABCM' körre (x-a)(x-b), XC állandó, tehát M' egy (x-a)(x-b)/c egyenletű parabolát fog kirajzolni. Ennek tükörképe, M mértani helye is parabola. (ugyanígy ki kell hogy jöjjön ha a C pont egy AB-bal nem párhuzamos egyenesen fut, vagy egy AB-ot tartalmazó hiperbolán. AB-t tartalmazó parabolára is csak kis koordinátageometriázás. Geometriailag fogalmam nincs miért van így)
[1737]: Adott A, B, C pont a síkon. A-n átmegy egy rögzített r egyenes, és egy futó f egyenes, B-n egy rögzített b1 egyenes. Legyen Fi:=bi f, ci egyenes legyen Fi és C pontokon átmenő egyenes, Ri:=ci f, ci egyenes legyen Fi és C pontokon átmenő egyenes, Ri:=ci r és bi+1 legyen a B-n és a Ri pontokon átmenő egyenes. Mi a mértani helye Fi pontoknak? r és bi+1 legyen a B-n és a Ri pontokon átmenő egyenes. Mi a mértani helye Fi pontoknak?
A válasz: Fi egy i-edrendű görbén fog mozogni. Konkrétabban az x^i egy elprojektált képén. A "feladat" úgy született, hogy az a művelet, hogy veszek a koordinátarendszerben egy x-en futó X pontot, és a rá merőleges x=X egyenest, ennek az y=1-el való metszését, ennek az x=1 egyenesre vonatkozó vetületét, ennek az origóból az x=X-re vetítését, S.Í.T, és ez a művelet pont egy x-szel való szorzás, tehát a mértani helye az x^i görbe, ennek elprojektáltja a feladat.
[1740]: Adott P pont és c kör, c körön O és O' pontok. O és O' középponttú, P-n átmenő körök metszése legyen M. Hol van M, ha O' -> O. Mi M (határértékének) mértani helye, ha O befutja c-t? Igazold, hogy minden P-n átmenő, k-n levő középponttú kör érinti M mértani helyét!
M pont P pontnak a k kör O-ban levő érintőjére vett tükörképe. Ezt nem tudom belátni. M mértani helyét ha leinvertáljuk P-re, akkor egy hipikét kapunk, aminek minden P-n átmenő, k-n levő középponttú kör képe, amely egy egyenes, az érintője. Azaz geometriailag, analízis vagy ilyesmi okoskodás nélkül be lehet látni, hogy sok kör burkológörbéje (amit mindegyik érint) megegyezik azzal a görbével, amit úgy kapunk, hogy vesszük két egymáshoz nagyon közel levő kör metszspontjait, és ennek a mértanihelye. (ha van valakinél még ilyen típusú feladat (vagy tud konstruálni) akkor azt nekemadhatná)
[1741]: adott e, f, g és h egyenes és egy P pont, szerkessz olyan p egyenest P-n át, hogy 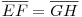 (ahol (ahol 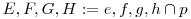 ) )
Ha EF=GH, akkor EH és GF felezőpontja ugyanott van. EH és GF felezőpontjának mértani helyei pedig hipikék, tehát két kúpszelet metszésével meg lehet szerkeszteni. (ez igaz minden kúpszeletre, hogy ha van egy kúpszeletem és egy pontom, akkor ha a pontból egyenesekkel metszem el a kúpszeletemet, és veszem a metszéspontok felezőpontjait, akkor azok mértani helye egy kúpszelet. Parabolára még nincs szép egyszerű bizonyításom.)
[1741]: adott e és f egyenes, P pont. Szerkessz olyan p egyenest P-n át, hogy 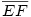 minimális legyen. ( minimális legyen. (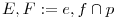 ) )
e és f metszéspontja legyen O. OP Thalész-körének és a P-n átmenő, e és f aszimptotájú hiperbolának a metszése legyen Q. PQ az az egyenes, amely átmegy P-n, és az e és f közé eső szakasza a legrövidebb. Ezt is itt hagyom belátni, vagy megcáfolni.
Másodrendű görbés szerkesztésekből is kéne nekem még több, hogy okosabb legyek másodrendű görbés szerkesztésekből.
|
| Előzmény: [1725] w, 2013-06-05 22:02:48 |
|
| [1743] Vonka Vilmos Úr | 2013-09-06 11:17:16 |
 Ez a megoldás talán inkább a projektív geometria témába illene, de sebaj.
Lemma. Legyen P az AB és A1B1 egyenesek közös pontja! Ekkor PF érinti k-t.
Bizonyítás. Legyen Y az XF érintő és BC közös pontja. Jelölje F' a k-hoz P-ből húzott AB-től különböző érintő és az XY egyenes metszéspontját. Azt kell megmutatnunk, hogy F' XY felezőpontja, azaz F'=F. Alkalmazzuk a Brianchon-tételt az 123456 hatszögre, ahol 1=2 az AC egyenes, 3=BC, 4=AB, 5=PF', 6=XY. Azt kapjuk, hogy A1B1, CF' és BX egy ponton megy át. Ismét alkalmazzuk a Brianchon-tételt, az AC és BC oldalak szerepének felcserélésével. Ekkor azt kapjuk, hogy A1B1, CF' és AY egy ponton megy át. A két eredményből együtt adódik, hogy az ABXY teljes négyszög AY BX átlóspontja illeszkedik CF'-re. Tehát F' XY-ra vonatkozó harmonikus társa a négyszög harmadik átlóspontja, ami az AB és XY egyenesek közös ideális pontja. Az ideális pont harmonikus társa azonban ismert módon a felezőpont. BX átlóspontja illeszkedik CF'-re. Tehát F' XY-ra vonatkozó harmonikus társa a négyszög harmadik átlóspontja, ami az AB és XY egyenesek közös ideális pontja. Az ideális pont harmonikus társa azonban ismert módon a felezőpont.
A lemma igazolása után rátérünk az állítás bizonyítására. Ehhez ismét a Brianchon-tételt alkalmazzuk a következő 123456 hatszögre: 1=6=AC, 2=3=AB, 4=PF, 5=XY. Ekkor 12 és 45 összekötő egyenese AF, 23 és 56 összekötő egyenese C1X, 34 és 61 összekötő egyenese PB1=A1B1. Így a Brianchon-tétel éppen a kívánt állítást adja.
|
| Előzmény: [1742] w, 2013-09-04 16:40:08 |
|
| [1742] w | 2013-09-04 16:40:08 |
 N+1-edik feladat. Legyen ABC tetszőleges háromszög, és k a beírt köre, ami a megfelelő oldalakat A1, B1, C1 pontokban érinti. Az AB-vel párhuzamos k-t érintő egyenes AC és BC közé eső szakaszának felezőpontja F, és az F-ből k-hoz AB-vel párhuzamosan húzott érintő AC-t X-ben metszi. Mutassuk meg, hogy XC1, A1B1 és AF egy ponton haladnak át.
|
|
| [1741] Sinobi | 2013-07-30 01:26:24 |
 március8 a szögharmadolás topicban:
,,Például egy ilyen: Adott a síkon két egymásra merőleges egyenes, és adott egy pont, amelyik az egyik adott egyenestől "p" távol van, a másik adott egyenestől "q" távol van. Szerkesztendő olyan egyenes, amely átmegy az adott ponton és amelynek a két adott egyenes közötti részének hossza "d". "
Ez érdekelne, de nem jöttem rá. Viszont például triviálisan megszerkeszthető kagylógörbe felvételével. De én polinomok gyökének megszerkesztése helyett (a polinomok csak koordinátázva kaphatók meg) inkább a görbézős szerkesztések felé mennék tovább.
Van két hasonló példám, amik kúpszeletelővel megoldhatók (egy kúpszeletelő kúpszeletet helyez néhány ponton és érintőn át, beleértve a végtelen távoli pontokat és egyenest is, és két ily módon kapott kúpszelet metszései szerkesztett pontnak számítanak)
első, ez egyszerűbb: adott e, f, g és h egyenes és egy P pont, szerkessz olyan p egyenest P-n át, hogy 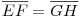 (ahol (ahol 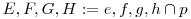 ) )
második: adott e és f egyenes, P pont. Szerkessz olyan p egyenest P-n át, hogy 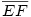 minimális legyen. ( minimális legyen. (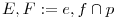 ) )
(nem biztos, hogy kúpszeletelők segítsége nélkül nem lehet őket megoldani)
|
|
| [1740] Sinobi | 2013-07-12 01:42:54 |
 Adott P pont és c kör, c körön O és O' pontok. O és O' középponttú, P-n átmenő körök metszése legyen M. Hol van M, ha O' -> O. Mi M (határértékének) mértani helye, ha O befutja c-t? Igazold, hogy minden P-n átmenő, k-n levő középponttú kör érinti M mértani helyét!
------
Adott e, f és g egyenes, g-n P és P' pontok. P pont merőleges vetülete e-re és f-re Pe és Pf, Pe-n és Pf-n átmenő egyenes legyen p. p' egyenes hasonlóan. Adott P esetén hol metszi p-t p', ha P' -> P?
-------
Adott O origó, z origó körüli forgatva nyújtás, e egyenes, rajta E és E'. zE:=z(E), és f legyen az E és zE pontokon átmenő egyenes, f' hasonlóan. Szerkeszd (találd) meg f és f' F metszésének helyét, ha E adott, és E' -> E. Mi F mértani helye, ha E végigfut e-n? Igazold, hogy minden E-re f érinti F mértani helyét!
(geogebrában a rögzített, kicsi sugarú körrel lehet az alakzatból kimetszeni olyan pontot, amely mindig rajta van az alakzaton, és mindig nagyon közel marad a kör középpontja futóponthoz)
|
|
|
| [1738] w | 2013-07-08 00:27:57 |
 Vonka Vilmos szép okfejtéséből kiindulva megkérdezhetjük, hogy mikor igaz, hogy a három átlót azonos arányban osztó pontok mikor vannak egy egyenesen.
|
| Előzmény: [1735] Sinobi, 2013-07-07 19:32:54 |
|
|
| [1736] Vonka Vilmos Úr | 2013-07-07 20:47:06 |
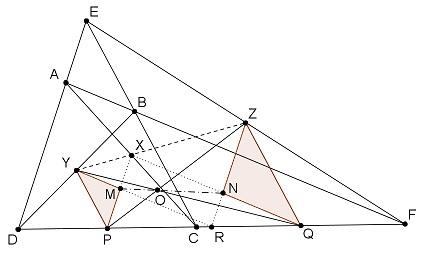
 Legyen az AC átló felezőpontja X, a BD átló felezőpontja Y, EF felezőpontja Z. Legyen továbbá P CD felezőpontja, Q CF felezőpontja és R DF felezőpontja. YP BCD középvonala, ZQ ECF középvonala, ezért YZ és ZQ egyaránt párhuzamos CE-vel. Tehát YP és ZQ párhuzamos. Hasonlóan: XP és ZR párhuzamos, valamint YC és QX is párhuzamos. Így az ábrán szereplő YMP és QNZ háromszögek megfelelő oldalegyenesei párhuzamosak, vagyis a két háromszög középpontosan hasonló. Tehát YQ, MN és PZ egy O pontra illeszkednek. Ekkor a Papposz-tételt a kollineáris PRQ és és MON ponthármasokra alkalmazva adódik az állítás.
|
 |
| Előzmény: [1735] Sinobi, 2013-07-07 19:32:54 |
|
| [1735] Sinobi | 2013-07-07 19:32:54 |
 Igazoljuk, hogy egy négyszög három átlójának felezőpontja (ahol a harmadik átló az átlóspontokat összekötő szakasz) kollineáris.
|
|
| [1734] Vonka Vilmos Úr | 2013-07-05 22:43:36 |
 Az első állítás nem igaz, pl. Geogebrával kísérletezve ez látható.
A második állítás igaz. Ismert ugyanis, hogy egy kúpszeletbe írt teljes négyszög átlóspontjai páronként konjugáltak egymáshoz, tehát bármely két átlóspont egyenesének a pólusa a harmadik átlóspont. Akármelyik kúpszeletet is tekintsük a paralelogramma csúcsain keresztül, a paralelogramma csúcsai által meghatározott teljes négyszög két átlóspontja ideális pont (a paralelogramma oldalegyeneseinek az irányai), a harmadik átlóspont pedig az átlók metszéspontja (azaz a paralelogramma szimmetriaközéppontja). Így az ideális egyenes pólusa - ami a kúpszelet centruma - éppen egybeesik az átlók metszéspontjával.
|
| Előzmény: [1733] Sinobi, 2013-07-05 22:21:40 |
|
| [1733] Sinobi | 2013-07-05 22:21:40 |
 Igaz-e, hogy egy deltoidon átmenő minden kúpszeletnek a deltoidéval azonos a szimmetriatengelye?
Igaz-e, hogy egy paralelogrammán átmenő minden kúpszeletnek a paralelogrammáéval azonos a szimmetriaközéppontja?
|
|
|
| [1731] w | 2013-07-02 07:42:29 |
 Igen, erre gondoltam. Az ilyen típusú feladatok közül talán a legalapabb ez, de már ki lett tűzve ebben a témában (jenei.attila), régesrégen.
|
| Előzmény: [1730] HoA, 2013-06-21 21:55:28 |
|
|
|
|
|
| [1726] Sinobi | 2013-06-06 12:02:40 |
 A mértani helyed nem lehet olyan csúnya, például megszerkeszthető az A-n átmenő egyenesekkel való metszése, vagy az AB-n átmenő körökkel való metszése.
Továbbá a mértani helyed félkörré fajul, ha az AB-vel párhuzamos egyenes messze van az AB egyenestől (mondjuk 1000-ben vagy 100000-ben metszi az y-t. Vagy mondjuk ő az ideális egyenes). Ez egyszerűen kijön, AB és AC egyenesek közelítenek a párhuzamoshoz, ACB szög meg a külső-belső szögfelezőjük szöge, azaz megközelítőleg derékszög.
|
|
| [1725] w | 2013-06-05 22:02:48 |
 A mértani helyed a GeoGebra szerint parabola, ezt majd igazolom. (Amúgy jól jön, nekem eléggé tetszik a parabola/hiperbola függvénytani megfogalmazásának geometriai alkalmazása.)
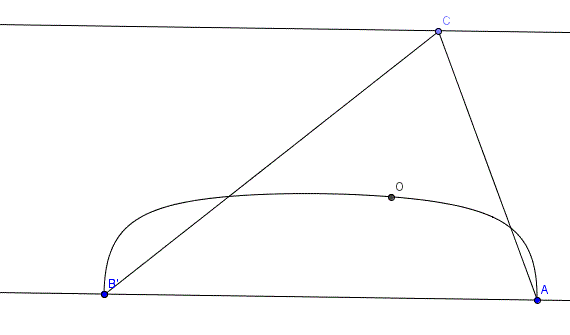
Mondanék egy sokkal nehezebb mértani helyt. Rögzített AB szakasz, AB-vel párhuzamos egyenesen mozog C, de most a beírt kör középpontjára keresünk mértani helyet. Igen csúnyácska lesz (ábra). A kérdés, hogy a te inverziódhoz hasonlóan mily módon lehet "normális" mértani helyre átírni a kérdést (eddig nyitott probléma :-) ).
Ugyanígy mozgó C pont esetén mi lesz a szimmediánpont mértani helye, i. e. konjugáljunk izogonálisan egy egyenest!
|
 |
| Előzmény: [1723] Sinobi, 2013-06-05 19:26:04 |
|
| [1724] w | 2013-06-05 20:03:06 |
 A megoldásom annyi, hogy vegyük észre, hogy 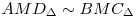 , hisz két-két azonos szögük van ha jól elnézem (itt M=AC , hisz két-két azonos szögük van ha jól elnézem (itt M=AC BD). Innen AM/BM=DM/CM. A csúcsszögek miatt is ekkor BD). Innen AM/BM=DM/CM. A csúcsszögek miatt is ekkor 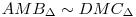 és ebből adódik a szögek egyenlősége. és ebből adódik a szögek egyenlősége.
Megfigyelhető, hogy vannak tipikusan olyan feladatok, melyek azonnal beugranak valamilyen embereknek, de mások pedig órákig töprengenek rajta. Emellett rendkívül érdekes, hogy egy lehetetlennek vélt, de sokszor átgondolt problémát egy másik embernek elmagyarázva, nagy eséllyel a magyarázás közben eszünkbe jut a megoldás. Személyes tapasztalat. :-)
Az ötlet a következő feladatból ugrott be. ABCD konvex négyszögben CBD =CAB =CAB és ACD és ACD =ADB =ADB . Igazoljuk, hogy BC, AD és AC szakaszokból szerkeszthető derékszögű háromszög. . Igazoljuk, hogy BC, AD és AC szakaszokból szerkeszthető derékszögű háromszög.
|
| Előzmény: [1721] Sinobi, 2013-06-04 22:08:52 |
|
| [1723] Sinobi | 2013-06-05 19:26:04 |
 wow, ez gyors volt, Nekem napokba telt, míg találtam egy (nem egyszerű) megoldást. A tiedet majd írd le ha ráérsz, addig is egy mértani hely:
Ha A és B rögzített, C egy AB-vel párhuzamos egyenesen futhat, mi ABC háromszög magasságpontjának mértani helye?
|
| Előzmény: [1722] w, 2013-06-05 07:25:33 |
|
| [1722] w | 2013-06-05 07:25:33 |
 Túl könnyű feladatok? Szeretek egy feladatot, ha nem trivi, de könnyen kijön érdekes eszközökkel.
A te feladatod nekem könnyű volt, talán mert láttam már hasonlót.
|
| Előzmény: [1721] Sinobi, 2013-06-04 22:08:52 |
|
| [1721] Sinobi | 2013-06-04 22:08:52 |
 w feladatai könnyűek, itt egy talán nehezebb (nekem nehéz volt)
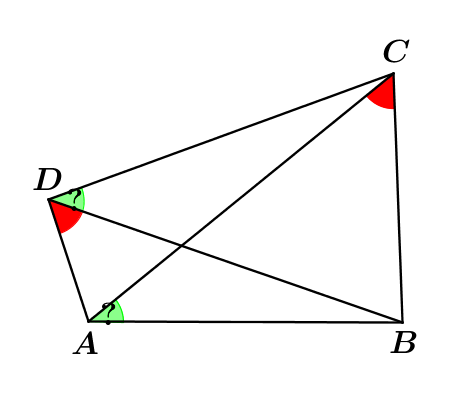
Néha előfordul, hogy a feladatban szögek adottak, és a bizonyítandó állítás is szépen megfogalmazható szögekkel. Ilyenkor az ember úgy szögszámolna egy kicsit, sűrűn használva, hogy a párhuzamos egyenesek között (tükörképek, elforgatottak, hasonló háromszögek etc) ugyanakkora a szög, és hogy a háromszög szögösszege 180, ebből minden ki kell hogy jöjjön, akkor is, ha nem trükközök semmit.
Feladat: AB szakasz ugyanakkora szögben látszik C és D pontokból, bizonyítsd be, hogy BC szakasz ugyanakkora szögben látszik A és D pontokból, anélkül hogy észrevennéd, hogy húrnégyszög és kerületi szögek, vagy felhasználnád annak a bizonyítását (sőt, ne is használj köröket).
|
 |
|
|
| [1719] w | 2013-06-04 20:59:25 |
 Egy háromszög beírt körének az oldalakkal való érintési pontjain át párhuzamost húztunk a szemközti szög szögfelezőjével. Mutassuk meg, hogy az így kapott három egyenes egy ponton megy át!
|
|
| [1718] w | 2013-06-04 20:21:14 |
 A és B egy O körüli k kör rögzített pontjai. E kör minden X pontjára legyen XO és k metszéspontja Y. Legyen M=AX BY. Határozzuk meg M mértani helyét. BY. Határozzuk meg M mértani helyét.
|
|
| [1717] ibiro | 2013-06-04 14:31:38 |
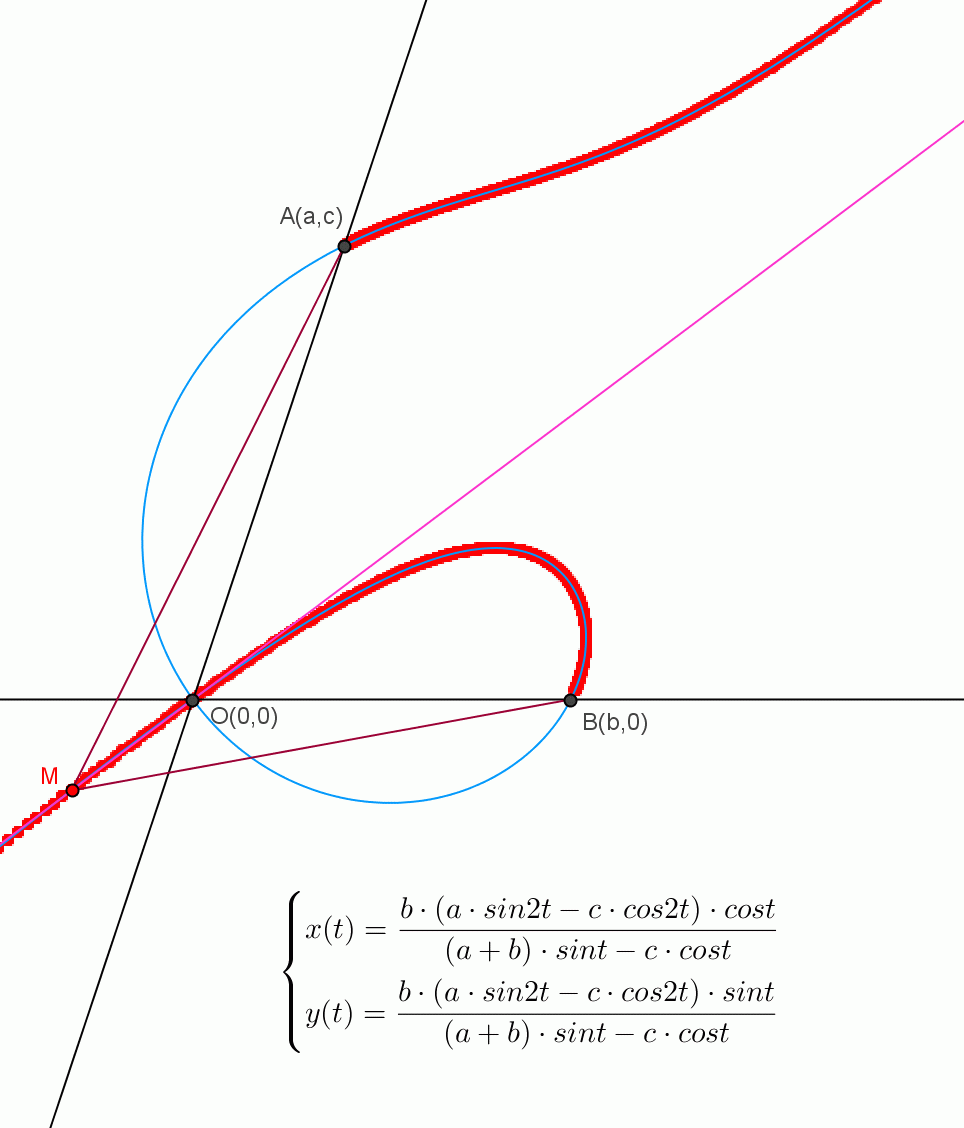
 Nem a szerkesztés volt a feladat, mert most már biztos hogy nem is lehet megszerkeszteni. Én állitom, hogy a feladat meg van oldva általánosabban, a kör csak leszűkiti a mértani helyet egy vagy maximum két pontra. Remélem a mellékelt ábra és a görbe parametrikus egyenlete mindenkinek világos. Köszönöm mindenkinek aki próbálkozott.
|
 |
| Előzmény: [1708] Sinobi, 2013-05-15 10:44:46 |
|
| [1716] Sinobi | 2013-05-20 00:22:29 |
 Igen, ez is jó szűkítés, nekem nem jutott eszembe. Jól számolom, hogy ez általában 6 db megoldást ad, és hogy minden esetben ad valamennyit?
Az én taktikám, hogy felépítem a kész ábrát az ABC köré, onnan már egyszerű átmozgatni.
Olyan háromszög szerkesztése ahol az oldalak párhuzamosak az eredetivel:
A, B és C ponton át párhuzamosokat húzok e,f és g egyenesekkel. Amelyek képei által alkotott E'F'G' háromszög oldalai párhuzamosak az eredeti EFG háromszögével, vagyis egy kpos nyújtással belevihetők - amellyel az eredeti háromszög a kívántba megy.
Amely egybevágó az eredetivel:
Ugyanúgy, mint az előbb, az e,f és g egymásal bezárt szögeivel látóköröket mérek ABC oldalaira, így kapok egy mozgatható, EFG-hez hasonló háromszögsort, és már csak azt kell megoldanom, hogy két kör metszéspontján át kívánt hosszúságú húrt tudjak szerkeszteni, de az sem nehéz.
|
| Előzmény: [1715] w, 2013-05-19 22:12:08 |
|
|
|
|
| [1712] Vonka Vilmos Úr | 2013-05-17 18:08:00 |
 A legegyszerűbb a keresett k körök e-re illeszkedő érintési pontjait megkeresni.
C rajta van az összes, A és B pontot tartalmazó kör közös hatványvonalán, ezért C-ből minden ilyen körhöz ugyanolyan hosszú érintőszakasz húzható. Ezért elég szerkeszteni egy tetszőleges kört az A és B pontokon keresztül, és ahhoz érintőt húzni C-ből, ennek a hossza adja meg az érintőszakaszok d hosszát. A keresett körökhöz C-ből húzott érintőszakaszok éppen az e egyenesen vannak, ezért a C középpontú d sugarú kör kimetszi a lehetséges érintési pontokat e-ből.
|
| Előzmény: [1711] jonas, 2013-05-17 17:41:22 |
|
| [1711] jonas | 2013-05-17 17:41:22 |
 Ha már a szerkesztéseknél járunk, hadd vessem föl a következő feladatot.
Bemenetnek adott síkon egy e egyenes, az egyenesen egy C pont, az egyenesen kívül egy A pont, és az AC szakasz belsejében egy B pont. Szerkesszük meg körzővel és vonalzóval mindkét kört, amely átmegy az A és B pontokon és érinti az e egyenest.
Mondok erre egy szerkesztést, de gyanítom, hogy van egyszerűbb megoldás is. Ha tudtok egyszerűbbet, akkor mondjátok el légyszi.
Szerkesszük meg az AB szakasz felező-merőleges egyenesét, ezt hívjuk f-nek. A keresett körök középpontja biztosan f-en van. Válasszunk az f egyenesen egy tetszőleges T pontot, amely nem esik az e egyenesre. Szerkesszük meg a T középpontú e-t érintő t kört – ismert, hogy ezt hogy lehet megszerkeszteni.
Most ha e és f nem párhuzamos, akkor jelölje e és f metszéspontját F. Ekkor a keresett két k kör hasonló a t körhöz egy-egy F középpontú hasonlósággal. Ha viszont e és f párhuzamos, akkor k egybevágó t-vel, és egy e-vel párhuzamos eltolással kaphatjuk meg belőle.
Szerkesszük meg most a b egyenest, amely B-n és F-en átmegy az első esetben, illetve B-n átmegy és e-vel párhuzamos a második esetben. Előfordulhat, hogy e és f majdnem párhuzamos ezért F lelógna a papírról, ilyenkor b-t például Desargues-tételes szerkesztéssel lehet megkapni. Legyen b és t két metszéspontja P (mindig van két metszéspont). Ekkor az az F középpontú hasonlóság vagy eltolás, ami t-t átviszi k-ba, a P pontot B-be viszi, ezért a TP egyenes párhuzamos a KP egyenessel, ahol K a keresett k kör középpontja. Ezért tehát szerkesszünk TP-vel párhuzamost B-n át, ennek a metszéspontja f-fel megadja a keresett K középpontot (mindig van metszéspont). Végül szerkesszük meg K középpont körül B-n át a k kört. Az utolsó lépéseket mindkét P metszéspontra el kell ismételni.
Ábrát most nem rajzolok, de ha nem érthető, akkor rajzolhatok később.
|
|
| [1710] Sinobi | 2013-05-15 23:12:56 |
 ,,Adott az e, f és g egyenes és egy háromszög. Szerkesszünk oly háromszöget, amelynek három csúcsa rendre e-n, f-en és g-n van, illetve hasonló a megadott háromszöghöz! A feltételeket lehet-e élesíteni?''
Élesíteni nem tudtam, de ilyeneket találtam:
ha nem mind a három egyenes párhuzamos, akkor szerkeszthető olyan háromszög, aminek minden oldala párhuzamos az eredetivel
ha létezik, akkor szerkeszthető olyan háromszög, ami egybevágó az eredetivel.
|
| Előzmény: [1705] w, 2013-05-14 22:10:14 |
|
|
| [1708] Sinobi | 2013-05-15 10:44:46 |
 Az enyém is ugyanígy kijön, ibiro feladatát tehát biztosan tudunk szerkeszteni már egy derékszögű hiperbolázóval és egy körzővel. Már csak azt kell belátni, hogy az összes ilyen hiperbola és körmetszés előáll, és beláthatjuk, hogy nem lehet megszerkeszteni általában.
|
| Előzmény: [1707] Sinobi, 2013-05-14 22:24:25 |
|
| [1707] Sinobi | 2013-05-14 22:24:25 |
 Az A-n átmenő egyenes csúsztatva tükrözött képe és metszése T pont. A két egyenes a csúsztatva tükrözés tengelyéből egy konstans hosszú szakaszt metsz le.
Ha nézed az erre merőleges tükrözést, az is ugyanez a tükrözés, és az a szakasz is konstans. Tehát két egyenestől való távolság szorzata is konstans.
|
 |
|
| [1706] Sinobi | 2013-05-14 22:15:01 |
 A piros az az eltolás vektor, a tengely meg a pirossal párhuzamos, és áthalad PQ felezőpontján. Csúszutatva tükrözés: egy tükrözés egy tengelyre, és egy csúsztatás egy vektorral (tetszőleges sorrendben).
|
| Előzmény: [1705] w, 2013-05-14 22:10:14 |
|
| [1705] w | 2013-05-14 22:10:14 |
 Ezt leírnád kicsit részletesebben? A stratégiát értem, de te pontosan mit csináltál a piros és zöld szakaszokkal, mi a tengely?
Amúgy köszönöm a hozzászólást!
"Ezt én is nem régen kaptam meg."
A feladatot egy versenyen találtam ki, és elemi megoldást most látok először rá :-). A feladat pedig úgy jött ki, hogy (alapja:)
Adottak a párhuzamos e és f egyenesek és közöttük a P és Q pont; szerk. olyan egyenlő szárú háromszög, amelynek alapja e-n van, szárszögcsúcsa f-en és P-n áthalad egyik szára, Q-n pedig a másik. (saját)
Ennek megoldása triviális tükrözés f-re. Akkor nézzük meg, hogy a tükrözéses módszert hogy vetnénk be akkor, ha e és f nem is párhuzamos. Keresd meg a kapcsolatot eközött és a végkifejlet között.
"Ahogy én kaptam: tekintsek egy csúsztatva tükrözést, bizonyítsam be, hogy egy egyenes és képe metszése egy derékszögű hipikén van."
Formálisan (vagy GeoGebrásan :-) ) megfogalmazva rögzítünk egy pontot, egy t tengelyt és egy v vektort; veszünk egy egyenest a ponton át és t-re tükrözzük majd eltoljuk v-vel; a kapott egyenest az eredetivel elmetszve kapott pont mértani helye kell ha az egyenes iránya befutja [- ;+ ;+ )-t. )-t.
"és még a gg is bugos és nem enged sok mindent"
Nekem 4.2 van és egész jól működik. Próbáld letölteni a legújabb verziót. Az ábrák alapján egész régi változat van neked meg.
-----
Van sok ilyen tükrözgetős fajta feladat. Elmondanék egy nem olyan triviálisat:
Adott az e, f és g egyenes és egy háromszög. Szerkesszünk oly háromszöget, amelynek három csúcsa rendre e-n, f-en és g-n van, illetve hasonló a megadott háromszöghöz! A feltételeket lehet-e élesíteni?
|
| Előzmény: [1704] Sinobi, 2013-05-14 20:43:47 |
|
| [1704] Sinobi | 2013-05-14 20:43:47 |
 Ezt én is nem régen kaptam meg.
Ahogy én kaptam: tekintsek egy csúsztatva tükrözést, bizonyítsam be, hogy egy egyenes és képe metszése egy derékszögű hipikén van.
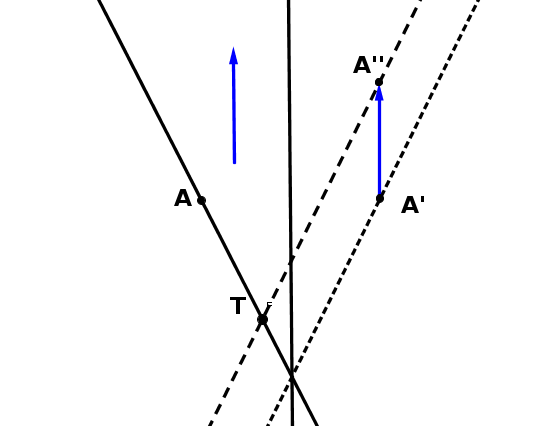
Egy csúsztatva tükrözés helyett rögtön kettőt nézek, a rá merőlegest, piros és zöld vektor-szakaszokkal (lásd ábra). Minden egyenespár metszése a tengelyekből (a hiperboláéból) egy piros és egy zöld szakasz, és mert az egyenesek tükrösek a tengelyekre, a T metszéspontnak a tengelyektől való távolságának szorzata mindig piros*zöld/4 (ha nem számoltam el) ami konstans, tehát ez egy 1/x függvény. (hogy ez miért hiperbola.)
(elnézést, az ábrára sok mindent zsúfoltam (és még a gg is bugos és nem enged sok mindent) )
Az enyém is hasonló, majd nekiesem.
|
 |
| Előzmény: [1703] w, 2013-05-14 19:18:04 |
|
| [1703] w | 2013-05-14 19:18:04 |
 Szerintem hasonló jellegű a belinkelt feladat. Talán a Steiner-tételt erre is rá lehetne nyomni? A másik az - amit gondolom észrevettél -, hogy hiperbolát invertálva és az alapkört mozgatva mindenféle szép őscsigát kaphatunk :-)
|
| Előzmény: [1702] Sinobi, 2013-05-14 17:38:05 |
|
| [1702] Sinobi | 2013-05-14 17:38:05 |
 felvettem az OB-n levő középpontú, O-n átmenő apollóniusz-köröket, leinvertáltam az ábrát O-ra, kaptam a következő feladatot:
Adott egy egyenesen B, O, rögzített, és egy F futópont. Adott az egyenesen kívül egy A pont. Hol lesz az FOA kör, és az FBF egyenes (BF felezőmerőlegese) metszéspontja? Geogebrában megnéztem, merőleges hiperbolának néz ki. Feladat: bizonyítsd be a sejtést, vagy cáfold (adj meg 6 metszéspont koordinátát úgy, hogy nem lesznek merőleges hiperbolán)
|
 |
| Előzmény: [1679] ibiro, 2013-04-05 13:09:20 |
|
| [1701] Maga Péter | 2013-05-02 08:18:47 |
 Általában nem mondhatjuk. Elnézést, ebből a szempontból az [1697]-ben leírt példa túl speciális volt, ahol véletlenül ez is igaz. De ugyanott legyen inkább a görbe f(t)=k(t2). Ekkor f'(t)=2tk'(t)=k(t)2tk'(0): itt a k(t) a csoportelem, amivel eltoljuk a 2tk'(0) Lie-algebra elemet (ami csak t=0-ban egyenlő f'(0)-val, f' látványosan nem invariáns). A képlet nem mondja azt, hogy a görbe érintője maga invariáns vektormező, az invarianciát csak a TeG és a TgG érintőterek természetes azonosításához használjuk.
Másképpen: azt nem tehetjük fel, hogy a görbe érintője (a mozgó pont sebessége) invariáns, de azt igen, hogy minden egyes pontban illeszkedik egy invariáns vektormezőre (ez persze lehet minden pontban más és más). Tehát a képletbeli gX érintő nemcsak az eltoláson keresztül függ g-től, hanem maga az X is mutat(hat) g-függést, ld. a fenti f(t)=k(t2) példát, ahol gyorsulva járjuk be a körvonalat.
|
| Előzmény: [1700] Lagrange, 2013-05-01 17:25:23 |
|
| [1700] Lagrange | 2013-05-01 17:25:23 |
 Na most már majdnem teljesen világos. A mozgás kijelöl egy görbét a Lie-csoporton, ennek a görbének a sebességét pedig egy X vektormezőnek tekintjük, ami egy adott g pontban a g görbe szerinti deriválás, tehát X(g)=dg/dt. Csak annyi a kérdés, hogy miért mondhatjuk a sebesség vektormezőre (ami matematikailag a görbe érintője) hogy az balinvariáns?
|
| Előzmény: [1699] Maga Péter, 2013-04-30 09:03:37 |
|
| [1699] Maga Péter | 2013-04-30 09:03:37 |
 ,,Ez a Lie-algebra definíciója, vagy az Exponenciális leképezéshez és a Hausdorff-Campbell formulához van köze? Vagy arról van szó, hogy egy vektormezőt egyértelműen meghatároz egy pontban felvett értéke?'' Hát, igazából minden mindennel összefügg, ahogy mondani szokás:). De a formulához a második mondatod a kulcs: ,,egy invariáns vektormezőt egyértelműen meghatároz egy pontban felvett értéke'' (természetesen ez nem igaz minden vektormezőre).
A wikipediás leírás szerintem használható, neked főleg a leképezés deriváltjáról szóló bekezdés kell, a leképezésed az Lg-1 eltolás.
|
| Előzmény: [1698] Lagrange, 2013-04-30 03:40:23 |
|
| [1698] Lagrange | 2013-04-30 03:40:23 |
 Köszönöm a választ.
Igazából az előre tolást meg visszahúzást értem, csak azt nem értem, hogy ez a képlet hogy jön ki. Ez a Lie-algebra definíciója, vagy az Exponenciális leképezéshez és a Hausdorff-Campbell formulához van köze? Vagy arról van szó, hogy egy vektormezőt egyértelműen meghatároz egy pontban felvett értéke? Szóval sokat olvastam erről a témáról, de nem áll össze a kép :S
Egy merev test mozgásának differenciálegyenletét kéne ennek segítségével levezetni, úgy, hogy a pályája a Lie-csoporton egy görbe, a sebessége meg a Lie-algebrájának egy eleme.
|
| Előzmény: [1697] Maga Péter, 2013-04-29 10:22:55 |
|
| [1697] Maga Péter | 2013-04-29 10:22:55 |
 Ha jól sejtem, ezzel az előretolás-vissahúzás dologgal vannak nehézségeid. Konkrét példák sokat tudnak segíteni, egy nagyon egyszerűt le is írok.
Legyen
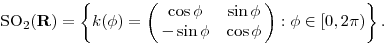
Modulo 2 számolva k( számolva k( )k( )k(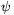 )=k( )=k( + +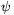 ). Most vegyük fel ezen a t ). Most vegyük fel ezen a t k(t),(t k(t),(t [0,2 [0,2 ]) görbét. Ennek deriváltja a k(t) pontban: ]) görbét. Ennek deriváltja a k(t) pontban:
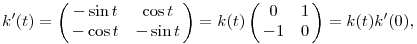
ahol k'(0) már a Lie-algebra eleme:
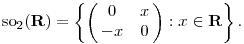
(A Lie-algebrát általában gót betűkkel jelöljük, de a fórum TeX-je nem érti a frak és mathfrak parancsok egyikét sem, ezért a kisbetű.)
Magyarán: vesszük az érintőt, visszahúzva az egységelembe megkeressük a neki megfelelő Lie-algebra elemet, majd azt előretoljuk. A kérdéses képlet csak ennyit mond.
|
| Előzmény: [1696] Lagrange, 2013-04-29 03:02:33 |
|
| [1696] Lagrange | 2013-04-29 03:02:33 |
 Üdv! Remélem valaki képen van differenciálgeometria terén. Arról lenne szó, hogy egy Lie-csoporton való mozgást kéne leírni differenciálegyenlettel. Konkrétan azt nem értem, hogy a (dg/dt)=gX egyenlet hogy jön ki. A képletben g eleme a Lie csoportnak, X meg a Lie algebra eleme, tehát egy vektormező, amit ugye úgy kapunk, hogy vesszük az egységelemnél az érintő térnek egy elemét. Eddig ahol olvastam visszahúzásokról (pullback) meg előretolásokról (pushforward) volt benne szó, de nem sikerült megértenem. Küldök egy képet is, hogy miről is van szó.
|
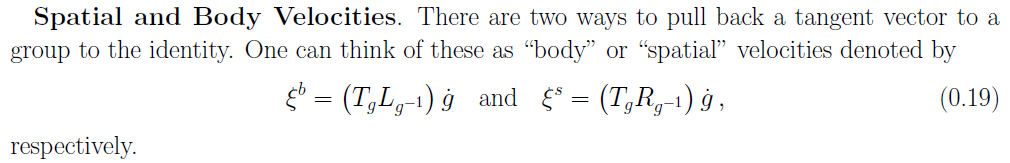 |
|
| [1695] Sinobi | 2013-04-28 00:34:29 |
 ,,Már látjuk, hogy nem lesz valami szép végeredmény"
Hé! Nekem tetszik!
Észrevehetted volna, hogy a kör tháleszkör, és az FDA< derékszög, így FDA ~ BFA.
felírva, hogy szögfelezőtétel: 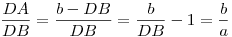 tehát tehát 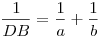
A hasonló derékszögű háromszögek miatt (befogótétel?): 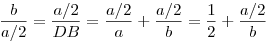
és ebből már szépen látszik is, hogy 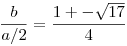
Ugyanilyen: ha egy háromszög egyik szöge derékszög, akkor a másik kettőt nem lehet úgy megválasztani, hogy a szögfelezőkre rakott kör átmennyen egy csúcson (megfigyelés). Bizonyítsd be a megfigyelést. Mekkora lehet egy háromszögben egy adott szög maximuma, hogy a másik kettőből lehessen alkotni Sinobi-tipusú háromszöget?
Két különböző eset, hogy a csúcson átmegy, vagy nem megy át a kör, nem tudom melyik milyen nehéz (megoldhatók-e egyáltalán elvadult koordinátázás nélkül).
|
| Előzmény: [1694] w, 2013-04-26 22:16:11 |
|
| [1694] w | 2013-04-26 22:16:11 |
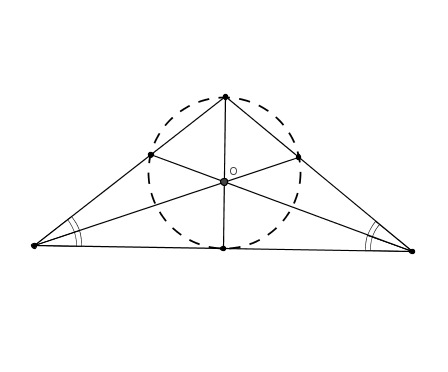
 Szép kis egyszerű feladat, kis ötlet kell hozzá. Ezért le is lőném. A szöveg kihagyja, de az ábrából felteszem, hogy a szárszög csúcsa van rajta a gondolt körön. Megjegyezném, hogy amúgy csak ez a csúcs lehet rajta.
Betűzzük le: legyen ABC a háromszög, ahol AB=AC=b és BC=a hosszú. Legyenek a szögfelezők talppontjai D AB, E AB, E AC, F AC, F BC. Szimmetria miatt a szereplő k kör érinti a BC alapot. Másrészt szögfelezőtétel miatt AD/DB=AE/EC=b/a, vagyis ráadásul BC. Szimmetria miatt a szereplő k kör érinti a BC alapot. Másrészt szögfelezőtétel miatt AD/DB=AE/EC=b/a, vagyis ráadásul 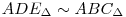 . Az ötlet az, hogy nagyítsuk ADE-t . Az ötlet az, hogy nagyítsuk ADE-t  =(a+b)/b aránnyal A-ból ABC-be, ekkor k képe ABC körülírt köre lesz, melynek átmérője =(a+b)/b aránnyal A-ból ABC-be, ekkor k képe ABC körülírt köre lesz, melynek átmérője 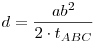 ismert képlet szerint. AF képe pont egy átmérő lesz, ahol AF az ABC háromszög magassága: AF=2tABC/a. Tehát felírható, hogy: ismert képlet szerint. AF képe pont egy átmérő lesz, ahol AF az ABC háromszög magassága: AF=2tABC/a. Tehát felírható, hogy:
d=AF.
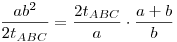
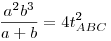 . .
Már látjuk, hogy nem lesz valami szép végeredmény, GeoGebra szerint ABC< kb. 38,7° lesz (ha megszerkesztjük). Akkor legyen az alapon fekvő szög x, a trigonometrikus területképletet behelyettesítve:
a2b3/(a+b)=a2b2sin2x
b=(a+b)sin2x
b=(2bcos x+b)sin2x
1=(2cos x+1)(1-cos2x)
Hát ha trigonometrikus egyenlet, akkor oldjuk is meg:
1=2cos x-2cos3x+1-cos2x
2cos3x+cos2x-2cos x=0
Új ismeretlen: y=cos x.
y(2y+y-2)=0
Mivel 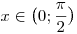 , ezért y=0 nem gyök. A másodfokú tag diszkriminánsa 17, gyökei , ezért y=0 nem gyök. A másodfokú tag diszkriminánsa 17, gyökei 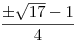 , ahol a pozitívra lesz szükség: , ahol a pozitívra lesz szükség: 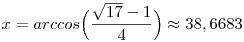 . (A könnyű érthetőség kedvéért szögben adom meg.) . (A könnyű érthetőség kedvéért szögben adom meg.)
Kitűnik még, hogy cos x szerkeszthető, ezért ABC háromszög is.
|
| Előzmény: [1693] Sinobi, 2013-04-26 20:11:26 |
|
| [1693] Sinobi | 2013-04-26 20:11:26 |
 Másik feladat: mekkorák annak az egyenlőszárú háromszögnek a szögei, ahol a szögfelezők talppontjaira illesztett kör átmegy a háromszög csúcsán?
|
 |
|
| [1692] Sinobi | 2013-04-26 20:08:45 |
 Borzasztó sok olyan görbe létezik, amin rajta van egy (na jó, kettő) meghatározott pont. :) Egyre kevésbé hiszem azt, hogy a feladatod megszerkeszthető, lehet, hogy létezik szép megoldás mondjuk vonalzóeltolással, fapálcikákkal, kötél és rajzszög alapú ellipsziszővel etc. de nem látok ilyet.
|
|
| [1691] ibiro | 2013-04-26 12:31:40 |
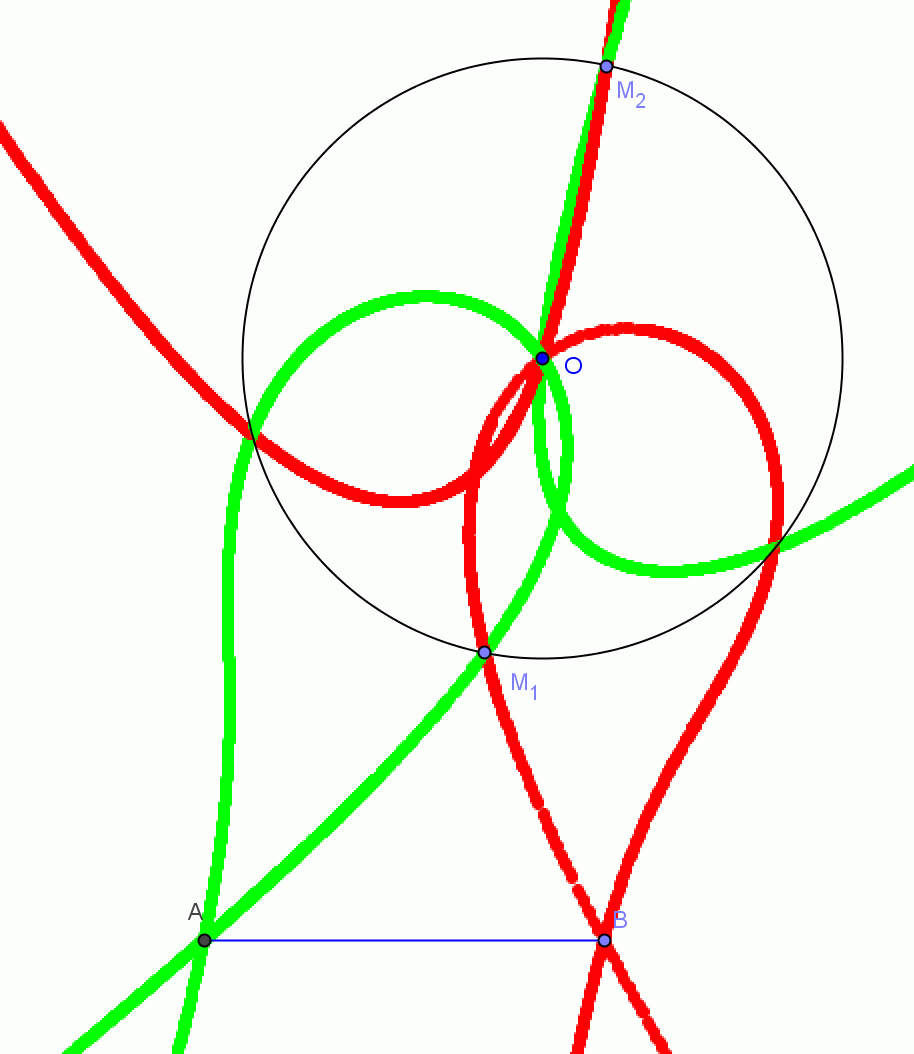
 "Mivel M1 ill M2 ellipszis pontok, nem kell bizonyítani, hogy MA + MB állandó ( az adott ellipszisen ) hisz ez az ellipszis definíciójából következik" ... de honnan veszed hogy ellipszis pontok - ez csak a te feltételezésed ! Bízonyisd be és akkor elhiszem.
Sinobi [1680] szerint egy "csúnya csigabigán", szerinted egy "elfajult ellipszisen" , szerintem pedig egy hurkon és egy parabolán vannak. Igaza van-e valakinek ??? Addig senkinek amig nem jön bízonyitással.
|
 |
| Előzmény: [1690] HoA, 2013-04-25 11:21:01 |
|
| [1690] HoA | 2013-04-25 11:21:01 |
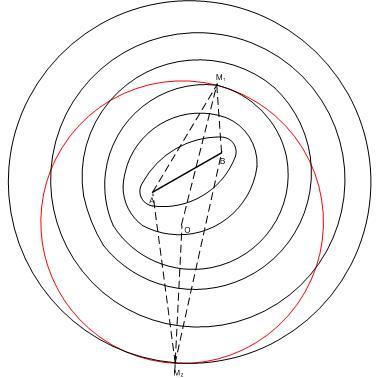
 A körön belüli általános helyzetű A és B pontokhoz mint fókuszokhoz tartozó ellipszisek az AB szakasztól, mint elfajult ellipszistől az "AB felezőpontja körüli nagyon nagy sugarú majdnem-kör" -ig ( elnézést a pongyola fogalmazásért ) folytonosan nőnek a nagytengely folyamatos növelésével. A legkisebbeknek nincs közös pontjuk a körrel. Lesz egy olyan, melynek egy közös pontja van a körrel, ez M1, ezután lesznek olyanok, melyeknek több közös pontjuk van a körrel. Eljutunk egy olyan nagy ellipszisig, melynek ismét csak egy közös pontja lesz a körrel M2 . Mivel M1 ill M2 ellipszis pontok, nem kell bizonyítani, hogy MA + MB állandó ( az adott ellipszisen ) hisz ez az ellipszis definíciójából következik. Talán csak annyiban kell szigorítani a fenti gondolatmenetet, hogy belássuk: ha egy körnek és egy ellipszisnek csak egy közös pontja van, akkor az érintési pont és így az itt húzott érintő egyenesek azonosak. Ebből már következik a feladat feltételének teljesülése.
|
 |
| Előzmény: [1689] ibiro, 2013-04-25 08:09:39 |
|
| [1689] ibiro | 2013-04-25 08:09:39 |
 Ehhez kellene bizonyitani hogy MA+MB állandó, de mi van akkor ha az ellipszis a kör belsejében lesz és nem érinti a kört ? A feladat nem mond semmit a kör és a szakasz helyzetéről.
|
| Előzmény: [1688] HoA, 2013-04-24 13:18:49 |
|
|
|
|
|
| [1684] Kemény Legény | 2013-04-20 19:06:18 |
 A koszinusztételes megoldást kicsi jobban "be lehet csomagolni" vektorok (és azok skaláris szorzatának) használatával. Ha az OA,OB,OC,OD,OP vektorokat rendre a,b,c,d,p jelöli, akkor
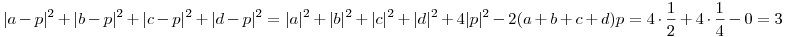 , mert a+b+c+d=0. , mert a+b+c+d=0.
|
| Előzmény: [1683] Layven, 2013-04-20 18:47:24 |
|
| [1683] Layven | 2013-04-20 18:47:24 |
 Igen, ez lehetőségként végig megvolt bennem, de az nem lett volna szép megoldás. Végül sikerült megoldani koordináták nélkül.(ABCD négyzet csúcsai, O a középpontja,P a kiválasztott pont a beírt körön.)
 , , 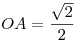
Koszinusztétel az AOP háromszögben:
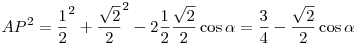
Felírva mindegyik oldalt hasonlóképpen és összegezve:
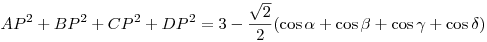
Most megmutatjuk, hogy a koszinuszok összege 0. A, O és C pontok egy egyenesben vannak, tehát AOP +POC +POC =180o, azaz =180o, azaz  + + =180o, hasonló módon pedig =180o, hasonló módon pedig  + + =180o =180o
Ismert, hogy 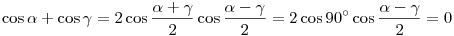
Hasonló módon kijön,hogy cos  +cos +cos  =0, tehát a koszinuszok összege valóban 0, vagyis AP2+BP2+CP2+DP2=3 =0, tehát a koszinuszok összege valóban 0, vagyis AP2+BP2+CP2+DP2=3
|
| Előzmény: [1682] Sinobi, 2013-04-20 12:32:17 |
|
| [1682] Sinobi | 2013-04-20 12:32:17 |
 Próbáld koordinátákkal. Vegyél fel egy P(Xp,Yp) pontot, és számold ki egy (mondjuk origó középponttú) egységnégyzet csúcsaitól a távolságnégyzetek összegét.
|
| Előzmény: [1681] Layven, 2013-04-20 11:32:22 |
|
| [1681] Layven | 2013-04-20 11:32:22 |
 A következő problémán akadtam fent: Bizonyítsuk be, hogy ha ABCD egységnégyzet beírt körén lévő pont P, akkor AP2+BP2+CP2+DP2=3
|
|
| [1680] Sinobi | 2013-04-13 19:10:10 |
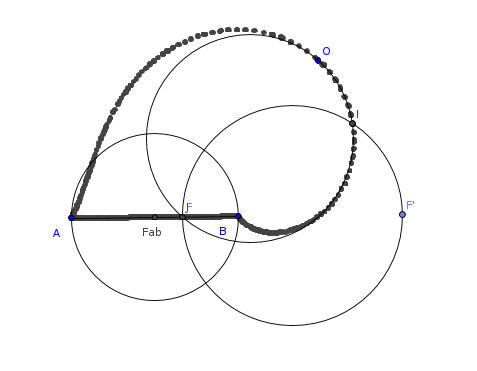
 Az olyan I pontok halmaza, ahol I rajta van AB F-hez tartozó szögfelezőkörén, és az FO tháleszkörén, (azaz AIB szögfelező talppontja F és FIO merőleges) egy csúnya csigabigán vannak. Kérdés: igaz-e, hogy ha meg tudjuk szerkeszteni valahogy a csúnya csigabiga és minden O középponttú kör metszéspontjait, akkor a csúnya csigabiga és egy tetszőleges kör ill. és egy tetszőleges egyenes metszéspontjait is.
|
 |
| Előzmény: [1679] ibiro, 2013-04-05 13:09:20 |
|
| [1679] ibiro | 2013-04-05 13:09:20 |
 Adott az AB szakasz és az O középpontú R sugarú kör. Határozzuk meg azt az M pontot (pontokat) a körön melyre az OM egyenes az AMB szög szögfelezője.
|
|
| [1678] HoA | 2013-04-04 14:16:15 |
 RE: "Q pontot pedig abban az esetben kapjuk, ha X a P pont PQ felezőmerőlegesére vett tükörképe"
Valójában Q pontot abban az esetben kapjuk, ha T a Q-ból e-re pocsátott merőleges talppontja és X a P pont T-re vett tükörképe.
|
| Előzmény: [1670] Vonka Vilmos Úr, 2013-04-03 13:10:24 |
|
|
| [1676] w | 2013-04-03 21:16:14 |
 Nem értem a bajt: egy triviális példát mondtál az állítás igazságára. Megint: ha egy téglalap kirakható 1xm-es és nx1-es lapok együttesével, akkor alkalmas lapot kiválasztva, csak azzal is kirakható.
|
| Előzmény: [1675] Róbert Gida, 2013-04-03 20:34:17 |
|
| [1675] Róbert Gida | 2013-04-03 20:34:17 |
 Legyen m=n=2, továbbá a nagy téglalap amit parkettázunk pedig 2x2-es. Ekkor ez kiparkettázható 1 x m -es és n x 1 -es téglalapokkal. De kiparkettázható csak 1 x m-es vagy csak n x 1-esekkel is.
|
| Előzmény: [1664] w, 2013-04-01 23:11:31 |
|
| [1674] Vonka Vilmos Úr | 2013-04-03 19:14:09 |
 A mértani hely meghatározására elemi megoldást egyelőre nem találtam, a hiperbolák fókuszait azonban meg lehet keresni.
Érdemes észrevenni, hogy mindkét hiperbola középpontja a PQ szakasz F felezőpontja. Valóban: ha például a T pontot F-re tükrözve kapott pontot T' jelöli és X'=e QT', akkor a keletkező szögek összevetésével nem nehéz látni, hogy ha PTX egyenlő szárú, akkor PT'X' is. Tehát ekkor T' is a mértani helyhez tartozik. QT', akkor a keletkező szögek összevetésével nem nehéz látni, hogy ha PTX egyenlő szárú, akkor PT'X' is. Tehát ekkor T' is a mértani helyhez tartozik.
Szóval a t hiperbolának az aszimptotáinak ismerjük az irányát (e-vel párhuzamos illetve merőleges egyenesekről van szó), és tudjuk, hogy F-re illeszkednek. Az aszimptoták ismeretében pedig szerkeszthetőek a tengelyek (szögfelezőként), és a hiperbola egy további pontjának (például P) ismeretében a fókuszok is. (Meg is szerkesztettem a fókuszokat; de azt nem látom egyelőre, hogy mi az elemi geometriai jelentésük, ami alapján elemibb megoldást lehetne adni a feladatra.)
Akkor néhány szó a Steiner-tételről. Két sugársor közötti projektivitáson a két sugársor közötti kettősviszonytartó, bijektív megfeleltetést értünk.
Tétel. Tekintsünk két sugársor között egy projektivitást. Az első sugársor minden egyenesének képezzük a metszéspontját a hozzá rendelt egyenessel. Az így kapott metszéspontok egy kúpszeletre (vagy speciális esetben egy egyenesre) illeszkednek. Amennyiben a metszési alakzat kúpszelet, az tartalmazza a sugársorok tartópontjait.
Vázlatosan egy viszonylag elemi bizonyításról: Legyenek a sugársorok tartópontjai P és Q, valamint a metszési alakzat három pontja A, B és C. Ez azt jelenti, hogy a projektivitásban a PA, PB, PC egyenesek képei rendre a QA, QB, QC egyenesek (a kettősviszonytartás miatt ez a három egyenespár egyértelműen meghatározza a projektivitást). Tegyük fel, hogy az A, B, C pontok nem kollineárisak; ekkor van egy és csak egy olyan k kúpszelet, amely az A, B, C, P, Q pontokra illeszkedik. (Öt pont egyértelműen meghatároz egy kúpszeletet, ez pl. a Pascal-tétel miatt ismert.) Azt kell ellenőriznünk, hogy egy D pont akkor és csak akkor illeszkedik k-ra, ha a tekintett projektivitásban PD képe QD. Másként fogalmazva: D akkor és csak akkor van k-n, ha a (PA,PB,PC,PD) és (QA,QB,QC,QD) kettősviszonyok egyenlőek. Ez azonban a kerületi szögek tételének alkalmazásával közvetlenül következik, ha egy kollineációt (tehát kettősviszonytartó leképezést) alkalmazva a k kúpszeletet körbe transzformáljuk. (A hozzáértők nyilván láthatják, hogy a bizonyítás nehézségeit hány ponton "kentem el" bizonyos "jól ismert" tényekre hivatkozva; a téma részletes kifejtése azonban jóval túlmutat a fórum keretein.)
|
| Előzmény: [1672] w, 2013-04-03 16:59:24 |
|
| [1673] w | 2013-04-03 17:33:18 |
 A Te feladatodra ez a megoldás nem igazán használja ki, hogy két dimenzióban van, nagyon szép ötlet.
Az általam kitűzött feladat térbeli változata "lemészárolható", csak a megoldással még várnék.
|
| Előzmény: [1668] Fálesz Mihály, 2013-04-03 10:01:27 |
|
| [1672] w | 2013-04-03 16:59:24 |
 A megjegyzésben szereplők érdekelnek leginkább. Mi Steiner tétele? Be tudnád-e bizonyítani? Létezik-e a feladatomnak elemi megoldása: hol és hogyan találhatjuk meg a két hiperbola fókuszait/vezéregyeneseit?
w
|
| Előzmény: [1670] Vonka Vilmos Úr, 2013-04-03 13:10:24 |
|
| [1671] Fálesz Mihály | 2013-04-03 14:48:35 |
 Nem értem.
"... a téglatest egy oldalára a kis téglatesteknek csak olyan lapja fekszik, aminek van egész oldala"
Miért ne lehetne valamelyik kis téglának az adott lapra merőleges éle az egész hosszúságú?
|
| Előzmény: [1669] jonas, 2013-04-03 10:24:34 |
|
| [1670] Vonka Vilmos Úr | 2013-04-03 13:10:24 |
 Gondolom, hogy úgy értetted a feladatot, hogy a Q ponton keresztül felvett tetszőleges másik egyenest rögzítjük, és azon a rögzített f egyenesen változik az Y pont.
Az egyszerűen látható, hogy mindkét mértani hely tartalmazza a P és Q pontokat. A t mértani hely esetén P=X választással adódik a P pont; a Q pontot pedig abban az esetben kapjuk, ha X a P pont PQ felezőmerőlegesére vett tükörképe.
További közös pontok csak abban az esetben találhatóak, ha e és f párhuzamosak. Valóban: tegyük fel, hogy M közös pont, és tekintsük az e illetve f egyenes M-hez tartozó X illetve Y pontját. (Tehát azokat az X illetve Y pontokat, amelyekből kiindulva a konstrukcióddal T=U=M adódik.) Ekkor PMX és QMY egyaránt egyenlő szárú háromszögek, valamint a (PMY) és (QMX) ponthármasok kollineárisak. Így a két egyenlő szárú háromszöget tekintve a szárszögek egybevágóak, ezért az alapon nyugvó szögek is. Ebből az e és f egyenesek párhuzamossága következik.
Az egyszerűen ellenőrizhető, hogy e és f párhuzamossága esetén a két mértani hely egybeesik: ebben az esetben az e egyenes valamely X pontjából kiindulva kapott T ponthoz TP f-et Y-nak választva U=T adódik. f-et Y-nak választva U=T adódik.
Összefoglalva: t és u közös pontjai pontosan P és Q, ha e és f nem párhuzamosak; ha pedig e és f párhuzamos, akkor az összes pont közös.
Megjegyzem, hogy t és u mindegyike derékszögű hiperbola. Az, hogy a mértani helyek kúpszeletek, projektív geometriai úton (Steiner tétele alapján) egyszerűen látszik. Például t ugyanis az e pontjait Q-ból vetítő sugársor és a PX szakaszok felezőmerőlegesei által alkotott sugársor metszési alakzata. Ez a két sugársor projektív kapcsolatban van, így a metszési alakzatuk kúpszelet. Ez a kúpszelet tartalmazza a sugársorok tartópontjait: tehát a Q pontot, illetve az e-re merőleges irányt jelentő ideális pontot. Tartalmazza továbbá e ideális pontját is, ugyanis abban az esetben, ha X az e egyenes ideális pontja, akkor T ugyanez az ideális pont. Így a mértani hely olyan kúpszelet, amelynek két ideális pontja merőleges irányokat jelent, azaz valóban derékszögű hiperbola.
|
| Előzmény: [1667] w, 2013-04-02 14:15:13 |
|
| [1669] jonas | 2013-04-03 10:24:34 |
 Ha az [1665]-ben lévő feladatot elhisszük, akkor ez az első térbeli változat már következik, hiszen a téglatest egy oldalára a kis téglatesteknek csak olyan lapja fekszik, aminek van egész oldala, ezért a téglatestnek kell lennie legalább két egész élének.
|
| Előzmény: [1668] Fálesz Mihály, 2013-04-03 10:01:27 |
|
| [1668] Fálesz Mihály | 2013-04-03 10:01:27 |
 Ne rohanjunk ennyire.
Oldjuk meg mindkét változatot, és keressünk olyan módszereket, amik magasabb dimenzóban is működnek. Pl. egy háromdimenziós téglát bontunk n×1×1, 1×m×1 és 1×1×k méretű darabokra, illetve olyan kis téglákra, amiknek van egész hosszúságű éle.
|
| Előzmény: [1667] w, 2013-04-02 14:15:13 |
|
| [1667] w | 2013-04-02 14:15:13 |
 Igaz, a két feladat nagyon ismert.
megoldás
Akkor inkább jöjjön egy nehéz, saját feladat. Még nem sikerüt megoldanom.
Adott egy e egyenes és rajta egy rögzített P pont, illetve egy másik Q pont a síkon. Legyen X e esetén fX a PX felezőmerőlegese, és T=fX e esetén fX a PX felezőmerőlegese, és T=fX QX. Hat. meg T pont t mértani helyét. Vegyünk fel egy tetszőleges másik egyenest is Q-n keresztül, rajta egy Y pontot, QY fY felezőmerőlegesét, és U=fY QX. Hat. meg T pont t mértani helyét. Vegyünk fel egy tetszőleges másik egyenest is Q-n keresztül, rajta egy Y pontot, QY fY felezőmerőlegesét, és U=fY PY pont u mértani helyét. Határozzuk meg t és u közös pontjait. PY pont u mértani helyét. Határozzuk meg t és u közös pontjait.
|
| Előzmény: [1665] Fálesz Mihály, 2013-04-02 09:02:25 |
|
|
| [1665] Fálesz Mihály | 2013-04-02 09:02:25 |
 Úgy már rendben.
Egy folytonos változat: ha egy T téglalapot fel lehet bontani kis téglalapokra úgy, hogy mindegyik kis téglalapnak van egész hosszúságú oldala, akkor T-nek is van egész hosszúságú oldala.
Tanulságos mindkét feladatot megoldani, és összehasonlítani a megoldásokat.
|
| Előzmény: [1664] w, 2013-04-01 23:11:31 |
|
| [1664] w | 2013-04-01 23:11:31 |
 Mindegy. Kicsit rosszul írtam ki (ahogy sejtettem :( ). A téglalapok nem forgathatók el, méreteik 1 x m és n x 1.
|
| Előzmény: [1663] w, 2013-04-01 22:52:37 |
|
|
|
| [1661] w | 2013-04-01 16:17:17 |
 Tudjuk, hogy egy téglalap kiparkettázható 1 x n -es és 1 x m -es téglalapokkal. Kiparkettázható-e csak 1 x n -es lapokkal vagy csak 1 x m -esekkel?
|
|
| [1660] w | 2013-03-29 20:03:47 |
 Ezt én nem tudom, nincs meg a tankönyv. Persze lehet spekulálni: szerintem a bizonyítás természetes, és egy középiskolás ezt értené meg legkönnyebben. Másrészt, felmerül, hogy van-e másik (megfordítási) bizonyítás erre, nincs nagyon esély módosításra.
|
| Előzmény: [1659] HoA, 2013-03-29 19:35:28 |
|
| [1659] HoA | 2013-03-29 19:35:28 |
 Köszönöm. Természetesen én is be tudom bizonyítani. Csak arra nem emlékeztem - és ezért erre lennék kíváncsi - , milyen bizonyítás szerepel ma a tankönyvben. Vagy tudod, hogy ott is ez van?
|
| Előzmény: [1658] w, 2013-03-29 18:55:50 |
|
|
| [1657] HoA | 2013-03-29 15:07:43 |
 Előre is elnézést a kérdésért: Hogy bizonyítja manapság a középiskolai tankönyv, hogy ha egy konvex négyszög szemközti oldalainak összege egyenlő, akkor érintőnégyszög? ( A másik irányra emlékszem :-) )
|
| Előzmény: [1646] Fálesz Mihály, 2013-02-27 19:22:17 |
|
|
|
|
| [1653] Fálesz Mihály | 2013-03-12 20:43:45 |
 A gömbháromszög területét nem határozza meg egy oldal és a hozzá tartozó magasság.
Valójában a terület használatára nincs is szükség, az euklideszi háromszögekben az 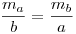 összefüggés egyszerű hasonlóságból jön ki. összefüggés egyszerű hasonlóságból jön ki.
|
| Előzmény: [1652] w, 2013-03-12 20:05:56 |
|
|
|
|
