|
| [1242] BohnerGéza | 2009-08-05 14:28:22 |
 Már picit gondolkodva is, nem csak szerkesztőprogrammal játszva:
Ha a nagy gamma (KLM) kör érinti a PQ-t, akkor azt az M felezőpontban teszi. Ekkor a KLM-kör R kp-ja egyenlő távol van P-től és Q-tól. Ha a feladat állítása igaz, M, R és O egy egyenesen van.
Ha ez mindig igaz, abból következik a feladat állítása.
Bizonyítsuk, hogy M, R és O egy egyenesen van!
|
| Előzmény: [1239] Fálesz Mihály, 2009-07-18 06:28:32 |
|
| [1241] HoA | 2009-08-05 08:09:20 |
 A 151. feladathoz: Szerkesztőprogrammal nézegetve úgy tűnik, hogy az EG szakasz F felezőpontja ABC háromszög beírt körének középpontja. Talán segít, ha először ezt bizonyítjuk.
|
| Előzmény: [1217] MTM, 2009-05-12 18:06:51 |
|
|
| [1239] Fálesz Mihály | 2009-07-18 06:28:32 |
 153. feladat (az idei matematikai diákolimpia 2. feladata).
Az ABC háromszög köré írt kör középpontja O. P és Q belső pontjai a CA, illetve AB oldalaknak. Legyen K, L és M a BP, CQ, illetve PQ szakaszok felezőpontja, és legyen  a K,L,M pontokon átmenő kör. Bizonyítsuk be, hogy ha a K,L,M pontokon átmenő kör. Bizonyítsuk be, hogy ha  érinti a PQ egyenest, akkor OP=OQ. érinti a PQ egyenest, akkor OP=OQ.
|
|
|
| [1237] sakkmath | 2009-06-15 15:54:30 |
 Hasznos volt egy kicsit kibontani a megoldás menetét, több szempontból is. Nekem például ezzel vált világossá, hogy valóban kulcsszerep jut az M pontnak. Melyről most már elárulhatjuk: ez a Miquel-pont, amely nemrég több itteni hozzászólás témája volt.
Múlik az idő, úgy tűnik, ideje feltenni a 152. feladatra egy olyan megoldást, amely a [1232]-ben közölt megoldásod a) megjegyzésére válaszol. Az ugyanitt javasolt 152/3. feladatra még megoldó kerestetik... . Később egyébként megnevezem a feladat elődjét, a megoldás elérhetőségét is megadva.
Következzék tehát a [1230]/152. példa egy újabb megoldása. Az 1. rész:
|
 |
| Előzmény: [1236] HoA, 2009-06-08 11:50:35 |
|
| [1236] HoA | 2009-06-08 11:50:35 |
 A leírtakkal egyetértek, sőt nagy részét evidensnek tartom. Megjegyzésem nem kívánt a kitűzés kritikája lenni. Ha már úgyis egy kicsit OFF vagyunk, leírom, hogyan jöttem rá én a megoldásra. Egyrészt hogy bemutassam, milyen értelemben „válik az M pont a megoldás kulcsává”, másrészt mert egy matematika oktatáshoz kapcsolódó fórumon talán nem baj, ha időnként ilyesmit is leírunk.
A három, egymást egy közös pontban metsző kör ábráját nézve feltünt, hogy az ábra szimmetrikus abban az értelemben, hogy egyik körnek sincs kitüntetett szerepe bármelyik másikkal szemben. Logikusnak véltem, hogy a megoldás is szimmetrikus: Ha a három körön futó pont valamelyike M-be kerül, akkor a másik kettő is. Ekkor persze vándorló háromszögünk elfajuló, egy pontra zsugorodik, alakjáról semmit sem mondhatunk – lásd NAGY BUMM hasonlatodat. De ha a futópontok közös M-beli helyzete megfelelő, akkor a feladat szabálya szerint a futópontok 180o-os elforgatottja, vagyis a - később indokolt módon - PaM,PbM,PcM -mel jelölt háromszög is megfelelő. Megrajzoltam PaM,PbM,PcM-et és úgy láttam, hogy oldalegyenesei áthaladnak az Mxy pontokon. Bebizonyítottam, hogy erre a háromszögre ez valóban igaz, és itt nekem is beugrott, valamelyik régi feladatban már szerepelt ez az ábra. Milyen jó lenne, ha a háromszögek többi helyzetében is az oldalegyenesek áthaladnának az Mxy pontokon! Beláttam, hogy tetszőleges ilyen Pa,Pb,Pc háromszög hasonló PaM,PbM,PcM-hez. Innen kezdtem el leírni a megoldást. A futópontok kezdeti felvétele tehát nem „Deus ex machina” módon, hanem az eddig leírtak alapján történt. Most már csak azt kellett igazolni, hogy az Mxy pontokra ileszkedő oldalegyenesekkel rendelkező háromszögek létrejönnek a futópontok kitűzésben leírt mozgása során.
|
| Előzmény: [1235] sakkmath, 2009-05-29 13:50:15 |
|
| [1235] sakkmath | 2009-05-29 13:50:15 |
 Örülök, hogy föltetted ezt a szép, a lényegre koncentráló megoldást! Köszönet érte. A feladatnak vannak egyéb, részben általad is jelzett, kidolgozásra érdemes részei, ezért most a magam részéről nem teszek ezeket érintő kiegészítéseket. Abban bízom, hogy valaki(k)nek lehetnek még saját eredményei(k) és 1-2 héten belül esetleg közli(k) azokat. Reagálnék viszont a kitűzési szöveggel kapcsolatos néhány megjegyzésedre, az estleges félreértések elkerülése végett. (Elnézést a terjedelemért.)
Mégegyszer: köszönöm és grat.
|
 |
| Előzmény: [1232] HoA, 2009-05-27 13:38:52 |
|
| [1234] m2mm | 2009-05-28 21:32:38 |
 Mivel a kör(ök) érinti(k) a tengelyeket, és (9,-2) pont x koordinátája pozitív, y koordinátája negatív, ezért a kör középpontjának x és y koordinátája ellentettei egymásnak, x pozitív, y negatív. A kör sugarának a hossza a középpont x koordinátájának nagysága, hiszen a kör érinti x-szet. A kör áthalad (9,-2) ponton, tehát: (9-r)2+(-2+r)2=r2, ahonnan r2-22r+85=0, amiből r értékére 5 illetve 17 adódik. Tehát a két kör egyenlete: (x-5)2+(y+5)2=25 illetve (x-17)2+(y+17)2=289.
|
| Előzmény: [1233] Luc, 2009-05-28 21:00:02 |
|
| [1233] Luc | 2009-05-28 21:00:02 |
 Sziasztok! Problémám akadt egy koordináta geometria feladattal: Meg kell adni annak a körnek(vagy köröknek) az egyenletét, amelyek áthaladnak (9;-2) ponton és érintik az x és y tengelyt is. Tudnátok segíteni, hogy hogy kell ezt kiszámolni?
|
|
| [1232] HoA | 2009-05-27 13:38:52 |
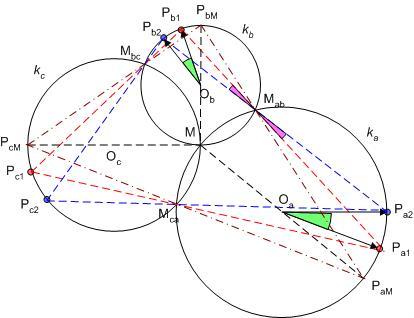
 1) Legyen a ka,kb,kc körök közös metszéspontja M, páronkénti második metszéspontjuk Mab,Mbc,Mca. Vegyük fel ka M-et nem tartalmazó MabMca ívén a Pa pontot. Legyen a PaMab egyenes és kb másik metszéspontja Pb , PbMbc egyenes és kc másik metszéspontja Pc . Könnyen belátható, hogy PcMca és McaPa párhuzamosak, vagyis egy egyenesen vannak. Különböző Pai -kat választva a keletkező PaiPbiPci háromszögek hasonlóak, hiszen például a Pai -knál fekvő szögek egyenlőek ka kör MabMca ívéhez tartozó kerületi szögével. Csak azt kell belátni, hogy ezen háromszögek csúcsai előállnak a feladatkitűzésben szereplő azonos, állandó szögsebességgel haladó futópontok egyidejű helyzeteként. Vegyünk fel két, 1-es és 2-es indexszel jelölt háromszöget. Pa1MabPa2 és Pb1MabPb2 szögek egyenlőek (csúcsszögek), a két körben a megfelelő ívhez tartozó kerületi szögek. Így a Pa1Pa2 és Pb1Pb2 ívekhez tartozó középponti szögek is egyenlőek, vagyis Pa és Pb ugyanakkora szögelfordulással jutnak ka-ban és kb-ben az 1-es helyzetből a 2-esbe, háromszögeink előállnak a feladatban megadott módon.
2) Nemcsak vándorló PaPbPc háromszögünk egyes helyzetei, hanem a részüket képező PaMPc háromszögek is hasonlók, hiszen egy-egy szögük az MMca húrhoz tartozó kerületi szög ka-ban ill. kc-ben. PaPbPc háromszög akkor lesz a legnagyobb területű, ha PaPc oldala a leghosszabb, vagyis ha PaMPc háromszög a legnagyobb. Ez pedig akkor következik be, amikor az M csúcshoz tartozó magasság a legnagyobb. Az utóbbi nem lehet nagyobb MMca -nál, és egyenlő is csak akkor, ha MMca merőleges PaPc-re. Legyen a csúcsoknak ez a helyzete PaM,PbM,PcM . A merőlegességből következik, hogy MPaM és MPcM átmérők – és ez belátható MPbM -re is.
Két megjegyzés:
a) Lássuk be, hogy háromszögünk akkor is megtartja alakját, mikor a ka-n futó pont az M-et tartalmazó MabMca íven halad.
b) PaM,PbM,PcM összetartozó ponthármas helyzetéből következik, hogy mindhárom körben 180o-ot fordulva mindhárom futópont M-be jut. Tehát , mint arra [1231]-ben utaltam, a körök metszéspontjában felvett futópont nem tilos, sőt a közös metszéspontban felvett 3 futópont éppen a megoldást adja.
152/3 feladatnak kitűzhetjük annak bizonyítását, hogy más megoldás nincs.
|
 |
| Előzmény: [1230] sakkmath, 2009-05-20 14:37:23 |
|
|
| [1230] sakkmath | 2009-05-20 14:37:23 |
 Az alábbiakban közlöm egy saját feladatomat. Nemrég rájöttem, hogy sajnos elődös: egy régi, közismert versenyfeladat következményének - vagy átfogalmazásának - is tekinthető.
152. feladat:
Egy adott ponton áthalad három, egymást páronként metsző kör. Mindegyik körön felveszünk egy-egy – a körök metszéspontjaitól különböző – pontot, melyek azonos körüljárási irányban befutják a körüket úgy, hogy egyszerre indulnak és azonos, állandó szögsebességgel haladnak.
1) Bizonyítsuk be, hogy e három pont felvehető úgy, hogy az általuk meghatározott háromszögek a teljes mozgás alatt hasonlóak legyenek egymáshoz.
2) Az így kapott háromszögek közül melyiknek a legnagyobb a területe?
|
|
| [1229] Editkesss | 2009-05-17 15:10:56 |
 De igen. A geometria nem az erősségem. (Ezeket a feladatokat már megoldottam . Abban viszont nem vagyok biztos, hogy jó is.) Ezért kértem segítséget!
|
|
|
| [1227] Editkesss | 2009-05-17 09:10:21 |
 Köszönöm szépen a segítséget! :) De lenne még egy-két feladatom! Az első: Tetszőleges e egyenes esetén jelölje: "Te" az e-re való tükrözést. Mutassuk meg, hogy ha "a" és "b" párhuzamos egyenesek, továbbá TaTbTcTaTbTc= identitás, akkor "c" is párhuzamos a-val és b-vel.
Második: Mutassuk meg, hogy ha az A1A2A3A4 és B1B2B3B4 négyszögek paralelogrammák, az AiBi szakasz Ai-hez legközelebbi negyedelőpontja Ni (i=1,2,3,4), akkor az N1N2N3N4 négyszög is (esetleg elfajuló) paralelogramma.
Előre is köszönöm!:)
|
|
| [1226] Euler | 2009-05-16 22:21:09 |
 A feladatot megpróbálom általánositva megoldani, vegyünk két nem egybeeső pontot, ekkor keressük azt a pontot a sikon, amelytől vett távolságaik négyzetösszege minimális, könnyen ellenőrizhető, hogy pont a két pontot összekötő szakasz felezőpontja lesz, pl. koordinátageometriával könnyen kijön,legyen A(a1;a2), B(b1;b2), a keresett pont: P(x;y), innen már csak egy másodfokú kifejezésnek kell vizsgálni a szélsőértkét, adódik az eredmény.Ez máshogy is kijöhet, bár itt nem biztos, hpogy "érdemes" igy gondolkodni, de ha mégis igy tesszük, akkor könnyen általánositható a probléma. Tudjuk ugyanis azt, hogy bármely háromszögben a szokásos jelölésekkel: 4sc2=2a2+2b2-c2(ez elég ismert összefüggésnek tekinthető,remélem.),a PAB háromszögre ezt felirva, kapjuk, hogy akkor lesz minimális a négyzetösszeg, ha a felezőponttól vett távolság minimális, máris adódik az eredmény. Kicsit továbblépve, vegyünk egy háromszöget(az egyszerűség kedvéért nem elfajulót), legyenek a csúcsai:A(a1;a2), B(b1;b2), C(c1;c2). keressük azt a pontot a sik egy adott egyenesén , amelytől vett távolságnégyzetösszeg minimális. Itt is hasonlóan eljárva, ráhúzodik a súlypontra az, ami előbb a felezőpontra húzodott rá,emiatt pedig az egyenesen lévő merőleges vetülete lesz a megfelelő pont.(Remélem érthető).Eljutottunk a Te problémádhoz, innen már "könnyű" elbánni vele, hiszen tekintsük az EBA és ECD háromszögeket, adódik, hogy akkor lesz mionimális a négyzetösszeg, ha az E-nek a CD és AB oldalak feletzőpontjától vett négyzetösszeg minimális, ez pedig használva az előzőeket, pontosan akkor lesz, ha a két felezőpont felezőpontjától vett távolság minimális, ez a pont pedig éppen a tetraéder súlypontja, ezt pl. vektorokkal lehet igazolni nagyon könnyen, igy itt a súlypontot kell merőlegesen vetiteni a sikra, ez lesz a keresett pont. Nyilván ha emeljük a dimenziószámot, hasonlóan adódik a feladat megoldása, csak maximum nem tudjuk elképzelni, hogy miről is szól a feladat. :-) remélem, tudtam segiteni a probléma megértésében.
|
| Előzmény: [1225] Editkesss, 2009-05-16 18:57:42 |
|
| [1225] Editkesss | 2009-05-16 18:57:42 |
 Hello, nekem egy olyan feladatom lenne, hogy adva van egy S sík és egy abcd tetraéder. veszünk egy E pontot . kérdés: Az S sík mely E pontjára lesz ez AE*2+BE*2+CE*2+DE*2 a kifejezés értéke a legkisebb? *2 a négyzetet jelöli!
|
|
|
| [1223] Vonka Vilmos Úr | 2009-05-15 15:46:44 |
 Akkor tényleg csak néhány ötlet:
1. és 2. Az adott ponton keresztül, amelynek a képét keressük, tekintsünk egy tetszőleges segédegyenest, és próbáld először ennek a képét megszerkeszteni.
3. A megfelelő egyenespár segítségével először határozzuk meg a kollineáció tengelyét, majd használjuk ki azt a tényt, hogy a centrum és az eltűnési egyenes távolsága megegyezik a tengely és az ideális egyenes képének távolságával.
4. A megfelelő egyenespár és egy pont ismeretében ismét először keressük meg a tengelyt. Majd válasszunk egy tetszőleges segédpontot azon az egyenesen, amelyiknek adott a képe; és próbáld a választott pont képét megszerkeszteni.
5. Az ABCD négyszög képe akkor lesz paralelogramma, ha a szemköztes oldalegyenesek metszéspontjaihoz a kollineáció ideális pontot rendel. Ez alapján határozd meg először az eltűnési egyenest. A tengely meghatározásához pedig tekintsünk ismét egy segédegyenest azon a ponton keresztül, amelynek a képe adott, és szerkesszük meg először a segédegyenes képét.
Remélem, innentől már menni fog!
|
| Előzmény: [1218] kandi, 2009-05-13 07:55:44 |
|
| [1222] kandi | 2009-05-15 10:42:38 |
 Köszönöm a linket, bár nem igazán értem az anyagot:( Amúgy centrális kollineációval oldhatók meg elvileg a feladatok és mi a projektív geometriával foglalkozunk. Ha mégis lenne még egy kis segítség mert én már kifuladtam a sz ötletekből?!
|
|
| [1221] jonas | 2009-05-14 21:55:55 |
 Én inkább ábrázoló geometriára tippelnék, bár szerencsére nekem nem kellett ilyesmit tanulnom, úgyhogy nem vagyok biztos, hogy valóban erről van szó.
|
| Előzmény: [1219] HoA, 2009-05-14 15:22:08 |
|
| [1220] HoA | 2009-05-14 16:14:44 |
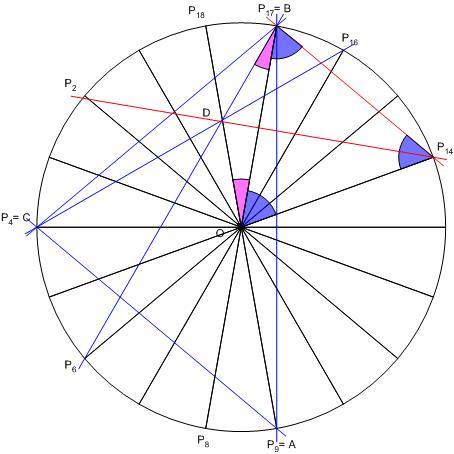
 Gratulálok! Igen, erre a megoldástípusra gondoltam! A D ponthoz tartozó bizonyításra egy másik változat: A definíció szerint D a P9P18 és P6P17 átlók metszéspontja, és azt kell igazolni, hogy P4P16-on is rajta van. DBO =20o ,mint a P6P8 ívhez tartozó kerületi szög. BOD =20o ,mint a P6P8 ívhez tartozó kerületi szög. BOD =20o ,mint a P17P18 ívhez tartozó középponti szög, OBD =20o ,mint a P17P18 ívhez tartozó középponti szög, OBD egyenlőszárú. P14OP17 egyenlőszárú. P14OP17 =60o ( 3 ívegység középponti szöge ) , P14OP17 =60o ( 3 ívegység középponti szöge ) , P14OP17 szabályos. Így BDOP14 deltoid, P17P14D szabályos. Így BDOP14 deltoid, P17P14D =30o . Így D rajta van a P14P17-tel 30o-ot bezáró P2P14 átlón és ennek P9P18 -ra vett tükörképén, P4P16-on is. =30o . Így D rajta van a P14P17-tel 30o-ot bezáró P2P14 átlón és ennek P9P18 -ra vett tükörképén, P4P16-on is.
|
 |
| Előzmény: [1216] sakkmath, 2009-05-12 15:24:47 |
|
| [1219] HoA | 2009-05-14 15:22:08 |
 Szia Kandi! Ez itt a KöMaL Geometria fóruma. Feladataid úgy látom, nem egészen a középiskolai geometria témájába tartoznak, ami még önmagában nem baj. Csak az nem világos, miről is van szó. A használt fogalmak alapján úgy gondolom, valamilyen projektív geometriai kurzusra jársz. A feladatok esetleg mind centrális kollineáció témába esnek? Ha nem ismered, talán segít ez a jegyzet:
http://www.jgytf.u-szeged.hu/~krisztin/projektiv.doc
|
| Előzmény: [1218] kandi, 2009-05-13 07:55:44 |
|
| [1218] kandi | 2009-05-13 07:55:44 |
 Szia Mindenki! Én még itt új vagyok, úgyhogy nem nagyon tudom, hogy hogyan működik, de nagy segítségre lenne szükségem. Van 5 db szerkesztési példám. Ami elvileg nagyon könnyű, de én nem tudtam megcsinálni, ha valaki segítene megköszönném. Leírom a feladatokat: 1., adott : tengely, centrum, eltűnési egyenes.Szerk. meg tetszőleges pont képét! 2., adott : tengely, centrum, ideális egyenes képe.Szerk. meg tetszőleges pont képét! 3., adott : az eltűnési egyenes, az ideális egyenes képe, és egy egymásnak megfelelő egyenespár.Szerk. meg a centrumot és a tengelyt! 4., adott : egy megfelelő pontpár, egy megfelelő egyenespár és a tengely egy pontja. Szerk. meg a centrumot és a tengelyt! 5., adott : a centrum és egy megfelelő pontpár. Határozzuk meg a tengelyt úgy, hogy egy előre adott ABCD négyszög képe paralelogramma legyen! Előre is köszönöm:)
|
|
| [1217] MTM | 2009-05-12 18:06:51 |
 151.feladat:
ABC háromszög körülírt körét, AB és AC oldalt rendre D, E, G-ben érinti egy kör. Bizonyítsuk be, hogy BDC szög felezője felezi EG szakaszt.
|
|
|
|
|
| [1213] sakkmath | 2009-05-12 15:20:18 |
 A HoA [1208]-as hozzászólásában kitűzött 150. feladat két feladatnak tekinthető. Elnézést, de sajnos csak négy részletben tudom feltenni a megoldást: a képek 50 KB-os határával a megfelelő képminőség ugyanis nem összeegyeztethető.
A megoldás 1. része:
|
 |
| Előzmény: [1208] HoA, 2009-04-29 15:00:17 |
|
|
| [1211] BohnerGéza | 2009-05-11 23:22:32 |
 Segítség a 150. feladat egy lehetséges megoldásához: Az E és D pontot máshogy definiálva lássuk be addíciós tételek következménye segítségével, hogy megfelelnek az eredeti definíciónak.
Egyelőre megpróbálok más jellegű (számomra szebb) megoldást is kitalálni.
|
| Előzmény: [1208] HoA, 2009-04-29 15:00:17 |
|
| [1210] HoA | 2009-05-07 22:43:48 |
 Mit néztél el? Szerintem a feladat jó. Nyilván sokunknak beugrik a hetedik, azonos sugarú kört és egymást érintő hat kör, és ezek befoglaló köre. De azt nem sikerült bizonyítanom, hogy a hetedik kör elhagyásával nem adható jobb megoldás - kisebb befoglaló kör.
|
| Előzmény: [1209] BohnerGéza, 2009-05-07 00:35:55 |
|
|
|
| [1207] BohnerGéza | 2009-04-17 13:56:24 |
 A 149. feladathoz: 2. rész.
Az előző [1206] hozzászólás folytatása.
A megoldásban nem törekedtem a teljességre, a legegyszerűbb megfogalmazásra, inkább a gondolatmenet bemutatására.
Jó lenne, ha valaki szebben megfogalmazott, vagy más jellegű megoldást is adna!
Vegyük észre a kapcsolatot az itt és HoA[1204] hozzászólásában látottak közt!
|
 |
| Előzmény: [1206] BohnerGéza, 2009-04-17 13:43:59 |
|
| [1206] BohnerGéza | 2009-04-17 13:43:59 |
 A 149. feladathoz: 1. rész.
Folytatása a következő hozzászólásban.
|
 |
|
| [1205] BohnerGéza | 2009-04-17 13:29:51 |
 Nekem is hiányérzetem volt janomo[1200] hozzászólásával kapcsolatban. Igaz így legalább HoA pontos, érthető megfogalmazásában láthattuk a megoldást!
Példát mutatok egy kevésbé szépre a következő hozzászólásban, az eredeti feladat kapcsán. Remélem, látható lesz belőle, hogy a szép megoldások is esetleg hosszabb gondolkodás után, sok munka árán, nem véletlenszerűen jönnek össze. Az így elért eredmény, sőt részeredmény is örömet adhat. (Ráadásul nem kell közben pl. négykerekű motoros marhasággal -nem jut eszembe a neve - tönkretenni a környezetet.)
149. feladat: A Surányi János emlékverseny 2. feladata: Az ABC háromszög beírt köre az AB és AC oldalakat rendre a D és E pontban érinti. A beírt körnek és az AEB háromszög köré írt körnek E-től különböző közös pontja legyen F, a D pont merőleges vetülete az EB egyenesen G. Igazoljuk, hogy 2ABEszög=BFGszög.
(Elnézést, a továbbiakban ezeket az eredeti jelöléseket használom!)
|
| Előzmény: [1204] HoA, 2009-04-17 09:10:46 |
|
| [1204] HoA | 2009-04-17 09:10:46 |
 Szerintem nem érdemes annyival elintézni az inverziós megoldást, hogy „inverzió a B pontra és kész”. Más feladatoknál is felhasználható például, hogy három, a póluson nem áthaladó egyenesen fekvő pont képe egy, a póluson átmenő körön van, és viszont: ha négy pont húrnégyszöget alkot – egy körön van – akkor egyiküket pólusnak választva a másik három pont inverz képe egy egyenesen fekszik.
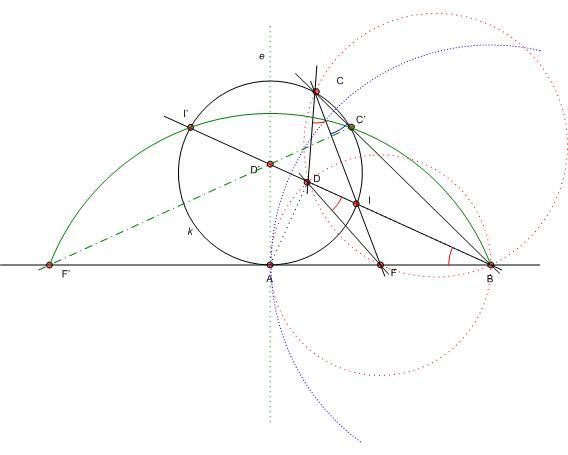
Legyen tehát az inverzió pólusa B, alapköre a k-t merőlegesen metsző kör. Ekkor k képe önmaga, A és A’ egybeesik, F képe az AB egyenes F’ pontja, melyre F’A = AB, AB Thálesz-körének képe az AB-re merőleges e egyenes, D képe, D’ BD és e metszéspontja, I képe a BI egyenes k-val alkotott második metszéspontja. CIF egyenes képe a B’, F’, I’ pontok által meghatározott kör. Ennek F’B húrja, e húrfelező merőlegese, tehát szimmetriatengelye. e k-nak is szimmetriatengelye, így a két kör metszéspontjai, C’ és I’ egymás tükörképei e-re. Ez igaz az F’, B pontpárra is, tehát a BD’I’ egyenes e-re vett tükörképe az F’D’C’ egyenes. A fentiek szerint ezért BCDF húrnégyszög, körülírt körében az egyenlő BF és DF húrokhoz egyenlő kerületi szögek tartoznak: DCF =FCB =FCB . .
|
 |
| Előzmény: [1200] janomo, 2009-04-04 12:18:33 |
|
| [1203] BohnerGéza | 2009-04-08 05:14:08 |
 148. feladat: Mekkora annak a legkisebb körnek a sugara, amelyben átfedés nélkül elfér 6 db 4 cm sugarú kör? (Érintkezés lehet.)
|
|
|
|
|
|
|
| [1197] BohnerGéza | 2009-04-01 19:15:28 |
 Köszönöm HoA! Elírtam. Helyesen a feladat:
A Surányi János emlékverseny 2. feladata alapján.
147. feladat: Érintse a k kör az AB egyenest az A pontban és legyen C a k egy A-tól különböző pontja, F az AB szakasz felezőpontja. Az FC messe még k-t az I pontban, az A-nak a BI-re eső merőleges vetülete D.
Bizonyítandó, hogy CF felezi a DCB szöget.
|
| Előzmény: [1196] HoA, 2009-04-01 16:15:55 |
|
|
| [1195] BohnerGéza | 2009-03-31 20:57:04 |
 Örülnék, ha nem csak HoA kapcsolódna be a 144. és 144.b feladat megoldásába.
Hogy jellemezhető pl. HoA 6 megoldása, hány és milyen megoldást adó P lehet még a háromszögön kívül?
|
| Előzmény: [1193] HoA, 2009-03-28 14:32:44 |
|
| [1194] BohnerGéza | 2009-03-31 20:48:12 |
 A Surányi János emlékverseny 2. feladata alapján.
147. feladat: Érintse a k kör az AB egyenest az A pontban és legyen C a k egy A-tól különböző pontja, F az AB szakasz felezőpontja. Az FC messe még k-t az I pontban, az A-nak a BI-re eső merőleges vetülete D.
Bizonyítandó, hogy CF felezi a DFB szöget.
|
|
| [1193] HoA | 2009-03-28 14:32:44 |
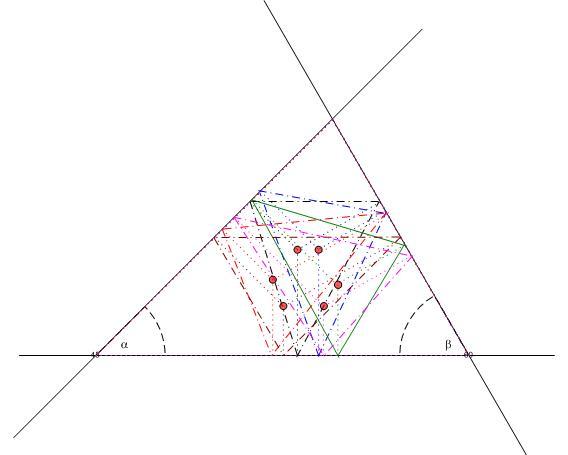
 144.b feladathoz: Az ABC háromszögön belüli P pontokra a talpponti DEF háromszögben a megfelelő pontok hat különböző helyzetben lehetnek szabálytalan hegyesszögű háromszög esetén, lásd [1190] ábráját. A [1189]-ben vázolt szerkesztést elvégezve mind a hat pontra kapunk megoldást az ábra szerint.
|
 |
| Előzmény: [1192] BohnerGéza, 2009-03-25 04:35:44 |
|
| [1192] BohnerGéza | 2009-03-25 04:35:44 |
 a 144. feladattal kapcsolatban:
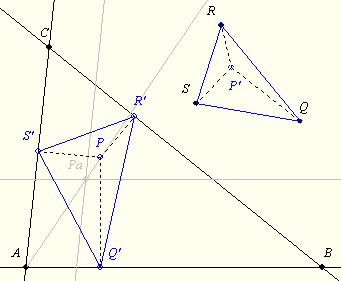
HoA nagy ötlete után példát mutatok az adott ABC háromszöghöz olyan P pont szerkesztésére, amelyhez adott QRS háromszöghöz hasonló talpháromszög tartozik:
Az ábra Q’PS’ szöge 180 fok-alfa, egyenlő a QP’S szöggel, így P’ számára adott vonal a QS szakasz 180 fok-alfa szögű látóköre. Hasonlóan pl. az RQ 180 fok-béta látóköre is, így P’ szerkeszthető.
A Pa pont SP’ távolságra van az AC-től és QP’-re az AB-től. P-nek az APa-n (és hasonlóan a BPb-n) kell lenni. …
Természetesen több megoldása lehet (van) a feladatnak. 144.b feladat: Adjuk meg a lehetséges megoldások számát!
|
 |
| Előzmény: [1188] HoA, 2009-03-22 19:52:41 |
|
| [1191] Maga Péter | 2009-03-22 22:33:02 |
 Szia! - 2 hónap késéssel, de...
Látom, hogy már kaptál segítséget, de ha dobsz egy e-mailt, akkor tudok küldeni egy anyagot. Nem egészen elemi, de annak idején (tavaly vagy tavalyelőtt) a debreceni Fazekas Gimnázium matek önképzőkörén mondtam el, és értették, legalábbis úgy tettek:).
|
| Előzmény: [1166] edu, 2009-01-23 09:22:12 |
|
|
|
| [1188] HoA | 2009-03-22 19:52:41 |
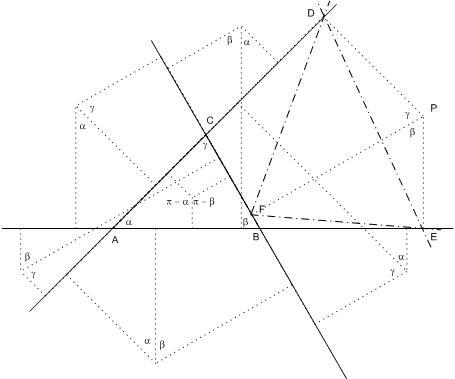
 Nevezzük a megfelelő P pont vetületei által meghatározott háromszöget P talpponti háromszögének. Mit állapíthatunk meg az adott ABC háromszög oldalegyenesei által hét tartományra osztott sík egyes részeiben a P-ből a talpponti háromszög csúcsaiba vezető szakaszok által bezárt szögekről? Az 1. ábráról leolvasható, hogy 2-2 tartományban ezek a szakaszok egymással nem egymás szögtartományába eső , szokásos szögmérési irányban mért (  , , ) , ( ) , (  , , ) illetve ( ) illetve (  , , ) szögeket zárnak be. A háromszög belsejében a megfelelő szakaszok szöge pl. ( ) szögeket zárnak be. A háromszög belsejében a megfelelő szakaszok szöge pl. (  – – , , – – ) )
A keresendő P pontok lehetséges helyzetét vizsgáljuk nem az ABC, hanem a talpponti, DEF háromszöghöz képest. Ezzel a keresett P pontok megszerkesztésének egy lehetséges útját is kijelöljük. Általános hegyesszögű ( 45, 60 75 fokos ) háromszöget választottam. ( Majd meg kell vizsgálni, hogy módosulnak az eredmények egyenlőszárú, egyenlőoldalú, derékszögű, tompaszögű, vagy akár más általános hegyesszögű háromszög esetében. ) Ha van megfelelő P pont az 1. ábra BC szakaszának A-t nem tartalmazó oldalán lévő síktartományban, akkor P-ből a DEF háromszög egy-egy oldala  ill. ill.  szög alatt látszik, mégpedig úgy, hogy P DEF egy-egy oldalának szög alatt látszik, mégpedig úgy, hogy P DEF egy-egy oldalának  ill. ill.  látószögű, a háromszög belseje felé eső körívén van. ( Mikor jöhetnek szóba a külső körívek? ) látószögű, a háromszög belseje felé eső körívén van. ( Mikor jöhetnek szóba a külső körívek? )
|
 |
| Előzmény: [1186] BohnerGéza, 2009-03-19 19:55:52 |
|
| [1187] fityfiritty | 2009-03-21 20:17:29 |
 Köszönöm.
Itt egy új, a számozottak között 146. feladat:
A hegyesszögű APD AP, illetve PD oldalának tetszőleges pontja rendre B, illetve C. Az ABCD négyszög átlói a Q pontban metszik egymást. M1, illetve M2 rendre az APD AP, illetve PD oldalának tetszőleges pontja rendre B, illetve C. Az ABCD négyszög átlói a Q pontban metszik egymást. M1, illetve M2 rendre az APD , illetve a BPC , illetve a BPC magasságpontja. Az ABQ és CDQ háromszögek körülírt köreinek Q-tól különböző metszéspontja legyen X, a BCQ és ADQ háromszögekre ugyanígy kapott pont pedig legyen Y. Bizonyítsuk be, hogy: ha az M1, M2 és X pontok egy e egyenesre esnek, akkor Y magasságpontja. Az ABQ és CDQ háromszögek körülírt köreinek Q-tól különböző metszéspontja legyen X, a BCQ és ADQ háromszögekre ugyanígy kapott pont pedig legyen Y. Bizonyítsuk be, hogy: ha az M1, M2 és X pontok egy e egyenesre esnek, akkor Y  e. e.
|
| Előzmény: [1182] HoA, 2009-03-16 16:59:04 |
|
| [1186] BohnerGéza | 2009-03-19 19:55:52 |
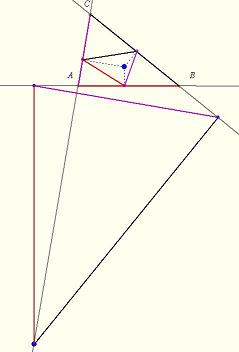
 A 144. feladathoz: Az ábrán látható két olyan (a két kék ponthoz tartozó) az eredetihez hasonló "talpháromszög", melyekben az AB-nek megfelelő oldal az AB és az AC egyenest köti össze.
Az előző hozzászólás ábráján is két ilyen van, a zöld és a barna ponthoz tartozó. ...?
|
 |
| Előzmény: [1185] BohnerGéza, 2009-03-19 17:53:44 |
|
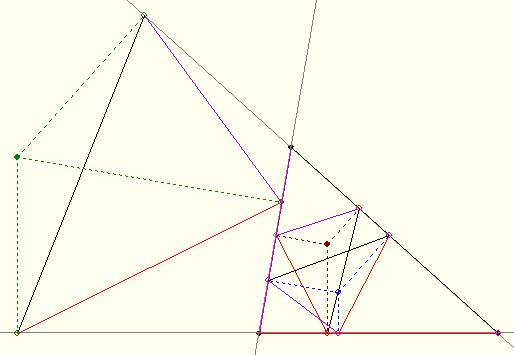
| [1185] BohnerGéza | 2009-03-19 17:53:44 |
 A 144. feladathoz: Az ábrán látható három, az eredetihez hasonló "talpháromszög".
A barna és a kék pont a háromszög Brocard-pontja. Azt nem nagyon nehéz bizonyítani, hogy a hozzájuk tartozó talpháromszögek megfelelnek a feladatnak, hogy ez a kettő egybevágó azt nehezebb.
A körülírt kör kp-jához tartozó középvonali háromszög is jó.
Az ábra zöld pontja is jó. ...?
|
 |
| Előzmény: [1173] BohnerGéza, 2009-02-16 20:08:53 |
|
|
| [1183] SmallPotato | 2009-03-17 22:57:39 |
 Találtam egy olyan irodalmat, amelyik talán érthetően vezeti le a dolgot. A 60-61. oldalakon van a Téged érintő/érdeklő rész. Ott y,x1,x2 változókról beszél, ezek a Te példádban (sorrendben) z,x,y.
A mintafeladatodat megcsináltam ezeknek az egyenleteknek a segítségével (a 61. oldal tetején a három egyenlet - mint egyenletrendszer - megoldása), és Excelben is (LIN.ILL függvény). Az eredmények teljesen megegyeznek.
A regressziós sík egyenlete a kis példádra, 6 értékes jegyre:
z=0,744949x+27,6667y-5898,09
Írj mailt, megküldöm az Excel-táblát.
|
| Előzmény: [1181] david20, 2009-03-16 12:01:19 |
|
|
| [1181] david20 | 2009-03-16 12:01:19 |
 Üdvözöllek!
Elolvastam a linkelt doksikat, és sok példát is találtam a neten, de valahogy nem akar kijönni...
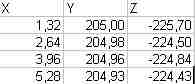
Tudna valaki egy kis példán keresztül segíteni a "regressziós sík" kiszámításában az alábbi pontokra.
Előre is köszönöm.
|
 |
| Előzmény: [1177] SmallPotato, 2009-03-11 01:09:43 |
|
|
| [1179] Gábor1905 | 2009-03-11 22:54:12 |
 Üdv. A következő kérdésre szeretnék választ kapni: Van-e olyan konvex 5, vagy attól többszög, aminek több mint 4 belső szöge 120°, vagy attól kisebb. Minden ötlet nagyon érdekel! Előre is köszönöm.
|
|
|
| [1177] SmallPotato | 2009-03-11 01:09:43 |
 Hogy a pontok mennyire pontosan vannak egy körvonalon, az - szerintem - gyakorlatilag mindegy. Ami nem mindegy: hogy egy síkban vannak-e. Ha nincsenek, akkor regressziós síkot kell keresni. (Ellenkező esetben nyilván bármelyik 3 pont kifeszíti a keresett síkot.) Regressziós sík megtalálására az irodalomban (pl. itt) találsz több megközelítést is (kiemelés tőlem):
"... egy, a megadott pontokhoz leginkább simuló általános kiegyenlítő sík egyenletét határozza meg, úgy, hogy a pontok és a sík közötti z irányú távolságok négyzetösszegét minimalizálja ..."
vagy
"... a megadott pontokhoz legjobban simuló kiegyenlítő sík egyenletét számítja ki úgy, hogy a pontok és a sík közötti merőleges távolságok négyzetösszegét minimalizálja ..."
Amit még találtam hirtelen: A regressziószámítás gyakorlati kérdései
Ha a regressziós egyenes megkeresésének módját ismered (így van vajon?), nem sok gondod lesz a síkkal sem.
|
| Előzmény: [1176] david20, 2009-03-10 13:12:11 |
|
| [1176] david20 | 2009-03-10 13:12:11 |
 Üdvözlök Mindenkit!
Egy kis segítségre lenne szükségem.
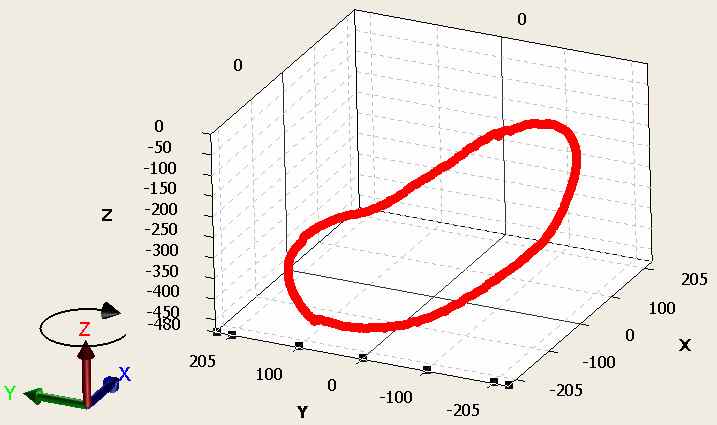
Adott egy térbeli koordináta rendszer, és 600 pont (X,Y,X), amik megközelítőleg (nem pontosan) egy kör körvonalán helyezkednek el. A kör síkja nem párhuzamos az XY síkkal.
A pontok a koordináta rendszerben való ábrázolása a képen látható.
Hogyan lehetne ezekre a pontokra egy síkot illeszteni?
Minden segítséget nagyon szépen köszönök.
David20
david20x@gmail.com
|
 |
|
|
|
| [1173] BohnerGéza | 2009-02-16 20:08:53 |
 144. feladat: Adott háromszög esetén határozzuk meg azon pontok halmazát, melyeknek a három oldalegyenesre eső merőleges vetülete az eredetihez hasonló háromszöget határoz meg.
|
|
| [1172] BohnerGéza | 2009-02-05 23:48:17 |
 HoA szép megoldása - az (1) tétel ismerete - után már könnyebb a következő feladat!
143/2. feladat: Bizonyítandó, hogy egy nem derékszögű háromszögnek és a magasságpontja oldalfelezőpontokra vonatkozó tükörképei által kapott háromszögnek ugyanazon ponthoz tartozó Simson-egyenese merőleges egymásra!
|
| Előzmény: [1170] HoA, 2009-02-05 20:03:36 |
|
|
| [1170] HoA | 2009-02-05 20:03:36 |
 Azért nem várok egy hetet, mert az alábbi megoldás nem csak a középiskolai anyagra támaszkodik, kihasználja a Simson egyenesnek azt a tulajdonságát, hogy
a körülírt kör két , P és Q pontjához tartozó Simson egyenes szöge megegyezik a körülírt kör PQ ívéhez tartozó középponti szög felével. (1)
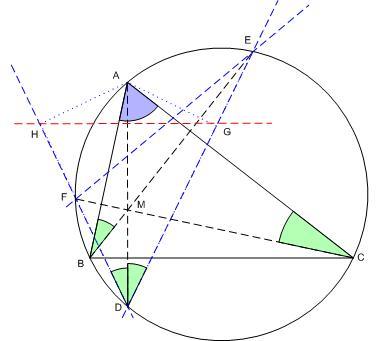
Ennek alapján elég az állítást a körülírt kör tetszőleges P pontjára belátni, hiszen P-t bármely más pontba mozgatva a két vizsgált háromszögre vonatkozó Simson egyenes ugyanazzal a szöggel fordul el, tehát megtartják merőlegességüket. Legyen az ABC háromszög magasságpontja M, az AM, BM, CM magasságoknak a körülírt körrel alkotott másik metszéspontjuk rendre D,E,F. ACF és EBA szögek egyenlőek, mert egy  szögű derékszögű háromszög harmadik szögei. Ezért az AE és AF ívek egyenlőek, és a hozzájuk tartozó EDA és ADF kerületi szögek is. Legyen P = A. Ekkor az ABC háromszögre vonatkozó Simson egyenes az AD magasságvonal. A-ból ED-re és FD-re bocsátott merőleges talppontja G és H. ADG és ADH egybevágó derékszögű háromszögek, G és H egymás tükörképei AD-re, ezért GH, az A pont EFG háromszögre vonatkozó Simson egyenese merőleges AD-re. szögű derékszögű háromszög harmadik szögei. Ezért az AE és AF ívek egyenlőek, és a hozzájuk tartozó EDA és ADF kerületi szögek is. Legyen P = A. Ekkor az ABC háromszögre vonatkozó Simson egyenes az AD magasságvonal. A-ból ED-re és FD-re bocsátott merőleges talppontja G és H. ADG és ADH egybevágó derékszögű háromszögek, G és H egymás tükörképei AD-re, ezért GH, az A pont EFG háromszögre vonatkozó Simson egyenese merőleges AD-re.
Talán tud valaki közvetlen, az (1) tételt nem felhasználó megoldást.
|
 |
| Előzmény: [1169] BohnerGéza, 2009-02-04 14:46:10 |
|
| [1169] BohnerGéza | 2009-02-04 14:46:10 |
 143. feladat: Bizonyítandó, hogy egy nem derékszögű háromszögnek és a magasságpontja oldalakra vonatkozó tükörképei által kapott háromszögnek ugyanazon ponthoz tartozó Simson-egyenese merőleges egymásra!
|
|
|
|
| [1166] edu | 2009-01-23 09:22:12 |
 Hi! A csak körzővel való szerkesztésekről keresek irodalmat. Különös tekintettel érdekelne egy adott kör középpontjának megszerkesztése (csak körzővel),ill. ennek bizonyítása (ha lehet elemi úton).A segítséget előre is köszönöm.
|
|
|
| [1164] HoA | 2009-01-14 17:47:33 |
 Vagy ugyanez másként: CD szakasz D végpontjában vegyük fel a CD-hez alfa/2 szögben hajló e egyenest. Ezt C középpontú a sugarú körívvel metszve kapjuk B-t. A diszkusszió így talán egyszerűbb: A megadott adatok között milyen összefüggés áll fenn, ha 0, 1 ill. 2 megoldást kapunk?
|
| Előzmény: [1162] jenei.attila, 2009-01-11 13:38:36 |
|
|
| [1162] jenei.attila | 2009-01-11 13:38:36 |
 b-t hosszabítsd meg A csúcson túl c-vel. Az így kapott végpontot jelöld D-vel, vagyis a CD szakasz hossza b+c lesz. Tekintsd a DBA egyenlő szárú háromszöget, amelynek A csúcsba futó szárai c hosszúságúak, a DB alapon fekvő szögei pedig alfa/2 nagyságúak, mivel az A-nál lévő külső szög alfa nagyságú, ami az ABC keresett háromszögünk A-nál lévő adott szöge. A szerkesztés menete: megszerkeszted az a, b+c oldalakkal bíró, alfa/2 nagyságú a-val szemközti szögű háromszöget (a fölé alfa/2 látószögkörív, amit a egyik végpontjából b+c-vel elmetszel; de gondolom ezt nem kell magyarázni). Megkapod, a már említett D pontot. felveszed B-ben a DBA alfa/2 nagyságú szöget. Ahol a szögszár elmetszi a CD szakszat, az lesz az A csúcs. Remélem érthető volt.
|
| Előzmény: [1161] nedijan, 2009-01-11 10:47:13 |
|
| [1161] nedijan | 2009-01-11 10:47:13 |
 Sziasztok!
Lenne egy egyszerű geometriai szerkeztésem, de sehogy nem jövök rá a megoldásra. Adott b+c, a és az a-val szemközti szög. Megszerkezthető-e a háromszög, ha igen adja meg a szerkesztés menetét! Ebben kérem a segítségeteket. Előre is köszönöm.
Jani
|
|
|
|
| [1158] HoA | 2008-12-06 20:33:36 |
 A paraméteres alakot talán úgy a legegyszerűbb felhasználni, hogy AQ és PQ merőlegességét írjuk fel. t-vel paraméterezve AQ = Q - A = ( 4t ; -2t; -3t ) PQ = Q - P = Q - A + A - P = ( Q - A ) - u = ( 4t -6 ; -2t + 4; -3t + 1) . A kettő szorzata 0. 4t ( 4t - 6 ) + 2t ( 2t - 4 ) + 3t ( 3t - 1 ) = 16t2-24t+4t2-8t+9t2-3t=29t2-35t=0 . t-vel oszthatunk - a 0 hosszúságú AA vektor bármire merőleges - , t = 35 / 29 , ami az előző levezetés számszerű eredményét adja.
|
| Előzmény: [1156] BohnerGéza, 2008-12-06 17:47:56 |
|
| [1157] HoA | 2008-12-06 19:00:36 |
 Ne ijesszük el farkasb-t, nem kell ide szélsőérték-számítás. Az X pont az AB szakaszt az AP szakasz és a PB szakasz AB-re eső vetületeinek arányában osztja. Legyen 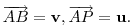 Ekkor Ekkor 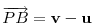 . X = A + m ( B - A ) = m B + ( 1 - m ) A , ahol m és ( 1 - m) aránya az u és a v - u vektor v -re vonatkozó vetületeinek aránya. Innen . X = A + m ( B - A ) = m B + ( 1 - m ) A , ahol m és ( 1 - m) aránya az u és a v - u vektor v -re vonatkozó vetületeinek aránya. Innen
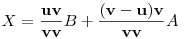
Számadatainkkal u = ( 6;-4;-1 ), v = ( 4;-2;-3 ), v-u = ( -2; 2; -2), uv = 35, (v-u)v = -6, v v = 29.
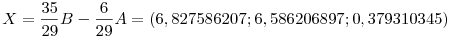 . vegyük észre, hogy az együtthatók összege 1, tehát X valóban az AB egyenes pontja és m > 1, így az ábrával ellentétben X az AB szakasz B-n túli meghosszabbítására esik. . vegyük észre, hogy az együtthatók összege 1, tehát X valóban az AB egyenes pontja és m > 1, így az ábrával ellentétben X az AB szakasz B-n túli meghosszabbítására esik.
|
 |
| Előzmény: [1154] farkasb, 2008-12-05 16:47:37 |
|
|
| [1155] Valezius | 2008-12-06 10:55:08 |
 Az egyenes pontjai ilyen alakúak: (2+4x, 9-2x, 4-3x) P távolsága egy adott ponttól: (8,5,3)-előbbi. Azaz (6+4x, -4-2x, -1-3x) Azt az x-et keressük amire a vektor hossza minimális. A hossza nem más, mint a koordináták négyzetösszege, aminek a szélsőértéke megkapható egy egyszerű deriválással.
|
| Előzmény: [1154] farkasb, 2008-12-05 16:47:37 |
|
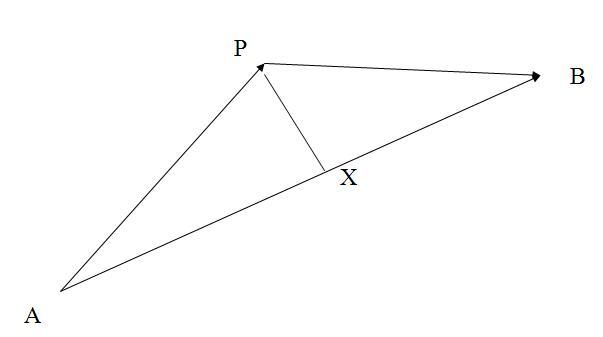
| [1154] farkasb | 2008-12-05 16:47:37 |
 Kedves Fórumozók!
Adott A(2,9,4) és B(6,7,1) ponttal meghatározott térbeli egyenes. Adott P(8,5,3) pont. Hogyan számolható ki a P pont vetülete az egynesen? Előre is köszönettel: farkasb
|
|
| [1153] HoA | 2008-11-30 19:48:12 |
 [1150] ábrájának tétele és a 142. feladat egyenértékűek. Jelöljük a D és E közötti piros pontot P-vel. A BE, CE, AD, BD egyenesek által meghatározott négy háromszög közül kettőnek a körülírt köre a P-n és E-n illetve a P-n és D-n áthaladó szaggatott körvonal. P tehát a négy háromszög körülírt köreinek közös pontja, a négy egyenes mint érintők által meghatározott parabola fókusza. A tétel bizonyítása tehát egyben a 142. feladat megoldása is.
Elemi, csak a húrnégyszögek szemközti szögeinek tulajdonságát felhasználó, lépésenként illusztrált bizonyítás található itt: http://agutie.homestead.com/FiLEs/miquel_pentagram1.htm
|
| Előzmény: [1150] BohnerGéza, 2008-11-24 10:16:28 |
|
| [1150] BohnerGéza | 2008-11-24 10:16:28 |
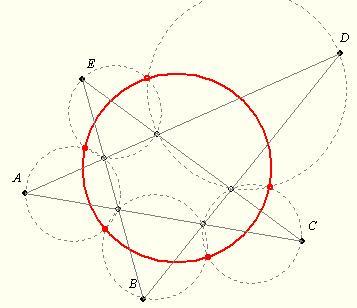
 A 138. feladathoz kapcsolódik:
A "Valaki mondja meg!" témában az [573]. hozzászólásban ábra is mutatja a következő tételt:
Ha négy egyenes négy háromszöget alkot, akkor ezek magasságpontjai egy egyenesen vannak, körülírt köreik egy ponton mennek át. Ez a pont és a magasságpontok egyenese parabolát határoz meg, melynek az eredeti 4 egyenes érintője.
Nem ismerek elemi megoldást a következő 142. feladatra:
Bizonyítandó, ha öt egyenes közül bármelyik négy négy háromszöget alkot, akkor az ezekhez a fenti tétel szerint tartozó fókuszok egy körön vannak.
A tétel egy érdekes következménye: Egy konvex ötszög minden +második csúcsát összekötve kapott öt háromszög körülírt köreinek "második" metszéspontjai egy körön vannak. Ábra! Segítségül: http://mathworld.wolfram.com/MiquelsPentagramTheorem.html
|
 |
| Előzmény: [1138] HoA, 2008-10-20 08:50:44 |
|
| [1149] HoA | 2008-11-15 08:07:57 |
 Én viszont teljesen egyetértek BohnerGézával! A [1146] -beli általános leírás és a [1148] -ban kifejtett következtetés együtt teljes mértékben kiváltják a konkrét példára végzett [1147] -beli levezetést. Elnézést kérek, hogy két lépés összevonását nem vettem észre [1146] végén.
|
| Előzmény: [1148] BohnerGéza, 2008-11-15 01:02:26 |
|
| [1148] BohnerGéza | 2008-11-15 01:02:26 |
 Kivételesen nem értek egyet HoA-val, bár ez sem teljesen igaz, csak ezért írom a következőt: Megfogalmazásom túlzottan tömör, komoly végiggondolást igényel, de szerintem teljes.
Az [1146]-ban leírtakból és az [1145]-ben lévő ábrából kiderül, hogy két forgatás szorzata végeredményben két olyan tükrözéssel helyettesíthető, melynek első egyenese az első forgatás kp-ján és az eredményül kapott forgatás kp-ján, a második a második forgatás kp-ján és az eredményül kapott forgatás kp-ján megy át, szögük az eredményforgatás szögének fele.
Kérem mindenkitől, ne adja föl, ha elsőre nem értette, amit írtam! Akarattal teszem, gondolkodást várok! (Ez nem HoA-nak szólt, jogosan figyelmeztetett mostani túlzott tömörségemre.)
|
| Előzmény: [1147] HoA, 2008-11-14 23:02:29 |
|
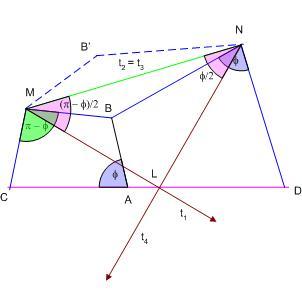
| [1147] HoA | 2008-11-14 23:02:29 |
 A leírtak egészen az utolsó mondatig rendben vannak. Ha az utolsó mondatot mint egy itt nem részletezett bizonyítás eredményét tekintjük, akkor az is elfogadható. De önmagában nem. Természetesen ha KM és KN merőlegesek, akkor a rájuk történő tükrözések eredője egy 180 fokos forgatás, vagyis egy K pontra vonatkozó tükrözés. De hát éppen ezt a merőlegességet kéne bizonyítani. A [1146] -ban leírt forgatáshelyettesítésből nem következik, hogy éppen MK és NK lenne az a két egyenes, melyeket t1 -nek és t4 -nek választhatunk. Szerintem a [1146] -beli gondolat feladatunk megoldására az alábbiak szerint használható fel:
Az M körüli  - - szögű forgatás helyettesíthető két, egymással ( szögű forgatás helyettesíthető két, egymással ( - - )/2 szöget bezáró, t1ést2 egyenesre vett tükrözéssel. Válasszuk t2 -nek MN -t, és legyen t1 az ezzel -( )/2 szöget bezáró, t1ést2 egyenesre vett tükrözéssel. Válasszuk t2 -nek MN -t, és legyen t1 az ezzel -( - - )/2 szöget bezáró, M-en áthaladó egyenes. Hasonlóan az N körüli )/2 szöget bezáró, M-en áthaladó egyenes. Hasonlóan az N körüli  szögű forgatás helyettesíthető két, egymással szögű forgatás helyettesíthető két, egymással  /2 szöget bezáró, t3ést4 egyenesre vett tükrözéssel. Válasszuk t3 -nak MN -t, és legyen t4 az ezzel /2 szöget bezáró, t3ést4 egyenesre vett tükrözéssel. Válasszuk t3 -nak MN -t, és legyen t4 az ezzel  /2 szöget bezáró, N-en áthaladó egyenes. Legyen t1 és t4 metszéspontja L. A két forgatás eredője, vagyis a négy tükrözés eredője, mivel a t2 -re és t3 -ra vonatkozó tükrözés eredője azonosság, a t1 -re majd t4 -re végrehajtott tükrözés eredője. /2 szöget bezáró, N-en áthaladó egyenes. Legyen t1 és t4 metszéspontja L. A két forgatás eredője, vagyis a négy tükrözés eredője, mivel a t2 -re és t3 -ra vonatkozó tükrözés eredője azonosság, a t1 -re majd t4 -re végrehajtott tükrözés eredője.
Az MNL háromszögben az M-nél és N-nél lévő szögek összege 90o , ezért a háromszög L-nél derékszögű. Másrészt a tükrözések eredője egy L köröli 180o -os forgatás - L-re vonatkozó tükrözés - és mivel a forgatások eredője C-t D-be viszi, L = K. Ezzel már valóban bizonyítottuk, hogy MK és NK merőlegesek.
|
 |
| Előzmény: [1146] BohnerGéza, 2008-11-11 23:30:46 |
|
|
|
| [1144] HoA | 2008-11-10 11:43:00 |
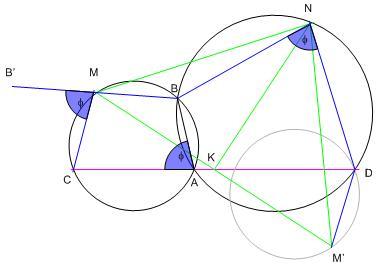
 A 141.feladat megoldása: Tükrözzük M-et K-ra, a tükörkép legyen M' .
a) Vegyük fel BM meghosszabbításaként az MB' = BM szakaszt. Jelöljük a BND szöget  -vel. ABND és ABMC húrnégyszög, ezért BAC és B'MC szög is -vel. ABND és ABMC húrnégyszög, ezért BAC és B'MC szög is  . Az ívfelezés miatt NB = ND és MB = MC (= MB') , a tükrözés miatt M'D = MC. ND az NB szakasz elforgatottja . Az ívfelezés miatt NB = ND és MB = MC (= MB') , a tükrözés miatt M'D = MC. ND az NB szakasz elforgatottja  -vel, a DM' -vel egyállású MC a BM -mel egyállású MB' elforgatottja -vel, a DM' -vel egyállású MC a BM -mel egyállású MB' elforgatottja  -vel, ezért NBM és NDM' háromszögek egybevágóak, NM = NM' . NK az MM'N egyenlőszárú háromszög alaphoz tartozó súlyvonala, tehát NK merőleges MK-ra. -vel, ezért NBM és NDM' háromszögek egybevágóak, NM = NM' . NK az MM'N egyenlőszárú háromszög alaphoz tartozó súlyvonala, tehát NK merőleges MK-ra.
b) Felhasználjuk, hogy egy X pont körüli  szögű és egy Y pont körüli szögű és egy Y pont körüli  szögű elforgatás eredője egy Z pont körüli szögű elforgatás eredője egy Z pont körüli  + + szögű elforgatás, speciálisan ha szögű elforgatás, speciálisan ha  + + = = , akkor egy Z pontra vonatkozó tükrözés. CMB szög = , akkor egy Z pontra vonatkozó tükrözés. CMB szög =  - - , az M körüli , az M körüli  - - szögű elforgatás C-t B-be viszi, az N körüli szögű elforgatás C-t B-be viszi, az N körüli  szögű elforgatás B-t D-be viszi, a két elforgatás eredője C-t D-be viszi. Mivel a két elforgatás eredője egy pontra vonatkozó tükrözés, ez a pont éppen K, tehát a két forgatás eredője egy K-ra vett tükrözés. Alkalmazzuk a két elforgatást M-re. Az M körüli forgatás M-et helyben hagyja, az N körüli forgatás egy olyan M' pontba viszi, melyre NM = NM' . Ugyanakkor M' éppen az M pont K-ra vett tükörképe. NK az MM'N egyenlőszárú háromszög alaphoz tartozó súlyvonala, tehát NK merőleges MK-ra. szögű elforgatás B-t D-be viszi, a két elforgatás eredője C-t D-be viszi. Mivel a két elforgatás eredője egy pontra vonatkozó tükrözés, ez a pont éppen K, tehát a két forgatás eredője egy K-ra vett tükrözés. Alkalmazzuk a két elforgatást M-re. Az M körüli forgatás M-et helyben hagyja, az N körüli forgatás egy olyan M' pontba viszi, melyre NM = NM' . Ugyanakkor M' éppen az M pont K-ra vett tükörképe. NK az MM'N egyenlőszárú háromszög alaphoz tartozó súlyvonala, tehát NK merőleges MK-ra.
|
 |
| Előzmény: [1143] BohnerGéza, 2008-11-05 23:18:14 |
|
| [1143] BohnerGéza | 2008-11-05 23:18:14 |
 A "kis segítség" önnálló feladatnak biztosan jó, ajánlom mindenkinek!
A 141. feladatra két megoldást ismerek, azokhoz nem használtuk ezt a segítséget, talán egy harmadikhoz jó.
Az általam ismett megodások alapszava:
- - - egyikhez: "ha felező..., akkor tükrözzünk rá!"
- - - másikhoz: "leképezések"
|
| Előzmény: [1142] HoA, 2008-11-05 11:24:39 |
|
|
