|
| [1648] nadorp | 2013-02-28 15:42:12 |
 A befogótétel csak derékszögű háromszögre alkalmazható, általános esetben sem. Inkább azon gondolkodj el, hogy minek a kiszámolásához használjuk leggyakrabban a háromszög magasságait?
|
| Előzmény: [1647] nyerek01, 2013-02-28 14:44:40 |
|
| [1647] nyerek01 | 2013-02-28 14:44:40 |
 Adott a lenti feladat: Egy háromszögben a=5,6 cm b=6,4 cm ma = 4 cm Mekkora mb? Befogotetellel probaltam megcsinalni, de elakadtam.
|
|
| [1646] Fálesz Mihály | 2013-02-27 19:22:17 |
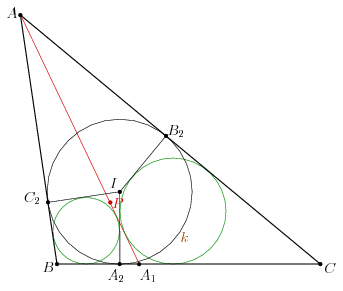
 A másik megoldást nem én találtam ki, a feladat kitűzőjétől származik.
Legyen I a beírt kör középpontja, az érintési pontok A2, B2 és C2. Az BA2IC2 és CB2IA2 deltoidokba írt körök egyik közös belső érintője az IA2 sugár. A másik közös érintő, csodák csodájára, átmegy az A csúcson...
|
 |
| Előzmény: [1645] Fálesz Mihály, 2013-02-27 19:10:32 |
|
| [1645] Fálesz Mihály | 2013-02-27 19:10:32 |
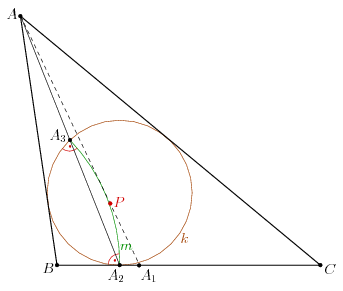
 Jó, mutatok két szerkesztést, de neked házi feladat kitalálni, hogy ezek miért működnek. Az elsőt én találtam ki.
Legyen k a beírt kör, A2 a k A-val szemközti érintési pontja, és legyen A3 az AA2 szakasz és k második metszéspontja. Legyen m az a körív a háromszög belsejében, ami A1-ban és A2-ben merőlegesen metszi k-t. Húzzunk A-ból érintőt m-hez; ez át fog menni a keresett P ponton, és kimetszi az A1 pontot a BC oldalon.
|
 |
| Előzmény: [1644] w, 2013-02-26 20:23:24 |
|
|
|
| [1642] w | 2013-02-23 17:33:59 |
 Na, ez már nem nehéz feladat, hanem szerintem elírás volt a Szőkefalvi-verseny kilencedikes fordulójában:
Adott ABC háromszög síkjában hat. meg azon P pontok halmazát, melyekre PA+BC=PB+AC=PC+AB.
|
|
| [1641] w | 2013-01-22 09:59:35 |
 Én is erre a megoldásra gondoltam (elvben). Talán még egyszerűbb lehetett volna, ha J-n keresztül párhuzamost húzol KL-lel, mert akkor a keletkezett szögek stb. tulajdonságait könnyebb megvizsgálni (meg természetes lépés, hogy igazolni akarjuk, hogy LM valamilyen módon középvonal). Nem feltétlenül kell akkor más, mint a 7. osztályos ismeretek, ami nem rossz egy olimpiai válogatóversenyről származó példától.
|
| Előzmény: [1640] HoA, 2013-01-22 00:31:15 |
|
|
|
| [1638] HoA | 2013-01-21 18:19:23 |
 Az mindenesetre látszik, hogy ha az arány a szögektől független állandó, akkor csak 1/1 ( felezés ) lehet, mert ha  növekszik és eléri a 90 fokot, akkor a két kör - és így O és J - egybeesik, AKOL = AKJL négyzet, melynek átlói felezik egymást :-) növekszik és eléri a 90 fokot, akkor a két kör - és így O és J - egybeesik, AKOL = AKJL négyzet, melynek átlói felezik egymást :-)
|
| Előzmény: [1637] w, 2013-01-20 16:02:33 |
|
|
|
|
| [1634] Fálesz Mihály | 2013-01-16 22:21:16 |
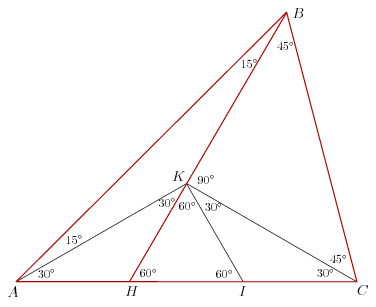
 Akkor egy megoldás csak egyenlő szárú háromszögekkel (és egy helyen tengelyes szimmetriával).
Legyen az AC másik harmadolópontja I, és rajzoljuk meg befelé a HIK szabályos háromszöget. A K pont a BH szakaszon van, mert AHB =120o. Az AH,HI,IC,HK,IK szakaszok egyenlőek. =120o. Az AH,HI,IC,HK,IK szakaszok egyenlőek.
Az AHK és CIK háromszögek egyenlő szárúak, innen kapjuk a bejelölt 30 fokos szögeket. Ezután BAK =15o, és az ABK háromszög is egyenlő szárú. Tehát AK=BK. A K rajta van az AC felező merőlegesén, így AK=CK. Végül a BCK háromszög is egyenlő szárú, mert BK=AK=CK, tehát BCK =15o, és az ABK háromszög is egyenlő szárú. Tehát AK=BK. A K rajta van az AC felező merőlegesén, így AK=CK. Végül a BCK háromszög is egyenlő szárú, mert BK=AK=CK, tehát BCK =CBK =CBK =45o. =45o.
|
 |
| Előzmény: [1632] w, 2013-01-16 19:44:03 |
|
| [1633] bily71 | 2013-01-16 22:20:37 |
 "- Valóban eltekinthetünk-e attól, hogy az S-en lévő háló oldalak nem egyenes szakaszok, hanem körívek?"
Eltekinthetünk, ha módosítunk kicsit az eljáráson, P csúcsait G1-re vetítjük, legyen A,B P két csúcsa, ekkor a köztük fut él illeszkedjen az A',B',O2 pontokon átmenő gömbi körre, ekkor az A'B' szakasz képe egy egyenesre illeszkedik, de ekkor további problémák léphetnek fel.
Egy másik mód, ha O pontból képezzük S síkra (mely sík illeszkedik P egy lapjára) P-t úgy, hogy minden él rövidebb, mint a képe, és a lapok képei nem fedik egymást, kivéve egy lapot, mely az egész képet fedi. Ilyen O pont létezik (számomra érdekes feladat volt meghatározni ezen pontok mértani helyét), de most már úgy látom, nem a leképezésen van a hangsúly, hanem F valamely tulajdonságán. Egyelőre elakadtam.
|
| Előzmény: [1625] HoA, 2013-01-07 10:28:40 |
|
| [1632] w | 2013-01-16 19:44:03 |
 :) Neked még hány ilyen "kalapácsod" van?
Van megfelelő eszköz, lehet nagyon elegáns (az alapvetőségi értelemben), de nagyon nehéz megoldást adni rá. Én max. az országos fordulón tűztem volna ki. Az előbbi hozzászólásomban felsorolt módszereket (tényleg, más nincs) alaposan át kell gondolni mindegyik lehetőséget. Tehát, találjunk egy alkalmas vonalat, amit behúzva csodák történhetnek!
|
| Előzmény: [1630] Fálesz Mihály, 2013-01-16 06:58:34 |
|
| [1631] HoA | 2013-01-16 09:11:02 |
 Rendben, azért még kérlek várj egy kicsit a "hetedikes" megoldás felrakásával. Hadd próbálkozzak egy [1615] jellegű pofonegyszerű változattal.
|
| Előzmény: [1629] w, 2013-01-15 17:49:16 |
|
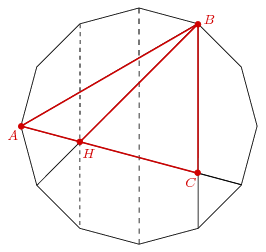
| [1630] Fálesz Mihály | 2013-01-16 06:58:34 |
 Az én hetedikes gyerekem is volt ugyanezen a versenyen. Egyetértek, a feladat nagyon szerencsétlen, ilyen szinten nincs megfelelő eszköz, később meg már van trigonometria, amivel a feladatot le lehet dózerolni.
Btw nekem van egy elég nagy kalapácsom az ilyenekre, ezúttal nem a szabályos 18- hanem a 12-szög átlói között kell keresgélni.
|
 |
| Előzmény: [1629] w, 2013-01-15 17:49:16 |
|
| [1629] w | 2013-01-15 17:49:16 |
 Legközelebb ilyen feladatot a Találjunk jobb megoldást! témába rakok :). A megoldásod szép és elegáns, középiskolás ismeretek mellett talán a legszebb.
A következő használható 7-8-adikos szinten: belsőszög-összeg, váltószög, háromszög nevezetes vonalai, spec. négyszögek, területképletek, egybevágóság, Thales és Pitagorasz (egész számokkal). Stratégiáik: számítsunk szögeket, szakaszokat; nézzük meg a magasság-, súlypontot, beírt és körülírt kör kp.-ját; húzzunk be egy alkalmas vonalat.
Ezt a feladatot a Bátaszéki verseny megyei (II.) fordulóján tűzték ki. Statisztikát kéne csinálni arról, hogy hányan csinálták meg, eddig senkiről sem tudok, aki megoldotta volna rendesen.
|
| Előzmény: [1628] HoA, 2013-01-15 11:35:56 |
|
| [1628] HoA | 2013-01-15 11:35:56 |
 Nem tudom, a 7. osztályos versenyzőktől elvárható-e a gyökvonás , a Pitagorasz-tétel és a nevezetes szögekkel bíró háromszögekben az oldalak és magasságok méretviszonyainak ismerete ( szándékosan nem írok szögfüggvényeket ) . Ha igen, akkor az alábbi típusú megoldást tartom elvárhatónak:
Az AB oldalon vegyük fel J-t úgy, hogy ABH és HBJ hasonló háromszögek, majd BH-n K-t úgy, hogy HBJ és JBK hasonló háromszögek. A 45 - 60 - 75 fokos szögekkel rendelkező AJH és HKJ háromszögekben AH és HJ ill. HJ és JK arányából adódik, hogy AH = 3/2 * JK, így AB = 3 * AJ. JH és BC párhuzamosak, beta = 60 fok.
|
| Előzmény: [1627] w, 2013-01-14 21:15:51 |
|
| [1627] w | 2013-01-14 21:15:51 |
 Kíváncsi vagyok, mit kezdetek a következő (mostani) 7. osztályos versenyfeladattal (én szinusztétellel indultam neki :) , a szöveget másképp írtam le).
184. feladat: Az ABC háromszögben A-nál 45 fokos szög van, és a B csúcsból az AH szakasz 15 fokos szögben látszik. Mekkorák a háromszög szögei, ha H az AC oldalon van, és (ACH)=1/2?
|
|
|
| [1625] HoA | 2013-01-07 10:28:40 |
 "mert az egy csúcsba futó élek által bezárt szögek összege kisebb, mint 360o"
Megmaradó aggályaim:
- Igaz, hogy az S-beli háló pl. F'' -ben összefutó szomszédos élei által bezárt szögek összege 360o , míg a konvex P F-ben ben összefutó szomszédos élei által bezárt szögek összege ennél kisebb. De mi garantálja, hogy az egyenlőtlenség a példánkban 3 szögpárra külön-külön is fennáll?
- Valóban eltekinthetünk-e attól, hogy az S-en lévő háló oldalak nem egyenes szakaszok, hanem körívek?
- És amire konkrét példám van: Nem változtatják-e meg az összehúzások a szögekre vonatkozó szükséges feltételeket?
Tegyük fel, hogy [1622] bal alsó ábráján az AF'' szakasz bal oldalán elhelyezkedő háló ötszög F'' -nél lévő szöge kb. 90o , mint az ábrán. Ebbe szépen elhelyezhető P AF-hez csatlakozó ötszögű lapja, melynek F -nél lévő szöge mondjuk 85o . Egy összehúzás után [1622] jobb alsó ábráját kapjuk, ahol az AF''' szakasz bal oldalán elhelyezkedő háló ötszög F''' -nél lévő szöge kb. 80o , mint az ábrán. Ide lefordítva P AF-hez csatlakozó ötszögű lapját, az ki fog lógni a rendelkezésre álló háló ötszögből.
|
| Előzmény: [1624] bily71, 2012-12-27 23:35:55 |
|
| [1624] bily71 | 2012-12-27 23:35:55 |
 Az élek második képe körív hiszen, ha O1-ből végigpásztázunk egy élet, akkor egy síkrészt kapunk, mely metszi a G1 gömböt, a metszet ekkor természetesen körív, így P egy élének első képe G1 egy főkörén van. Ha invertáljuk ezt a kört, akkor megint kört kapunk, vagyis egy él második képe az S síkon fekvő körön van. Mindezeket figyelembe vettem, de egyszerű ábrát akartam készíteni, mert valójában ennek nincs jelentősége. Az E''G' ívből mindegy mi lesz, mert P átforgatásakor az újonnan S-re érkező csúcsok nem lehetnek benne a vetület megfelelő összehúzásokkal már módosított tartományában a következő okok miatt.
Az összehúzást L-1-gyel kezdjük, majd átbillegtetve P-t L1 élein összehúzzuk a megnyúlt szomszédjait is. Utoljára az (ii) szerint kiválasztott L2-t húzzuk össze. Az L1 lap és szomszédai egy síkidomot határoznak meg S-n, melynek körvonala és L1 szomszédainak közös élei mentén, kivéve L2 azon éleit, miket F metsz, az S át van vágva. Miután L1-et a szomszédaival összehúztuk, a kapott síkidom körvonala eltávolodik a régi körvonaltól, mégpedig az összehúzott lapok irányába, így az összehúzott lapok nem metszetnek bele a nem összehúzott lapokba. L-1 szomszédai az összehúzás után nem metszethetnek bele L1-be, sem egymásba, hiszen L1-t szomszédaival együtt kiterítve a síkba a szomszédok közös élei nemhogy fedik egymást, hanem eltávolodnak egymástól. Ez azért van, mert az egy csúcsba futó élek által bezárt szögek összege kisebb, mint 360o.
Mikor L2-t és szomszédait összehúzzuk, az L1 és L2 szomszédai által alkotott síkidom új körvonala eltávolodik a régitől, mint az előbb, tehát ez a síkidom sem metsz bele a nem összehúzott lapokba, vagyis nem keletkezik átfedés. L2 még nem összehúzott szomszédait összehúzva (itt is billegtetünk L3 a végére hagyva) az L2 újonnan összehúzott szomszédai nem metszetnek bele L2-be, sem egymásba ugyanazon okokból kifolyólag, mint amit leírtunk már L1 és szomszédai esetében. L2 újonnan összehúzott szomszédai nem metszethetnek bele az előbb összehúzott lapokba sem, hiszen akkor belemetszenének L2 már előzőleg összehúzott szomszédaiba is, ami nem lehet megint csak az előbbiekben már említett okokból. Átfedés tehát itt sem keletkezett.
Az előbbi gondolatmenetet alkalmazhatjuk L3-ra, L4-re és így tovább...
A lényeg még egyszer: Lk újonnan összehúzott szomszédai nem metszethetnek bele az előzőekben összehúzott lapok által alkotott síkidomba, mert akkor belemetszenének Lk már előzőleg összehúzott szomszédaiba is, ami nem lehet, mert az egy csúcsba futó élek által bezárt szögek összege kisebb, mint 360o.
|
| Előzmény: [1623] HoA, 2012-12-27 15:04:35 |
|
| [1623] HoA | 2012-12-27 15:04:35 |
 További kellemes évvégét és évelejét mindenkinek!
Nem tudom, figyelembe vetted-e, és mert nem befolyásolja eredményeidet, egyszerűsítetted [1622] ábráját, minden esetre az S síkon a kétvesszős pontokat összekötő vonalak nem egyenes szakaszok.
[1617] metszet ábrájában persze a metsző sík O1 -en és O2 -n is áthalad, így az A'B' gömbi főkör ívet O2 -ből S-re vetítve egyenest kapunk. Ez azonban általában nem így van. A'B' az O1AB sík és G1 metszésvonala, G1 főköre. Ha ez nem megy át O2 -n, akkor a vetület S-en zárt görbe ( emlékezetem szerint kör ) lesz, melynek egy ívdarabja a háló A''B'' közötti vonala.
[1622] ábrája ígéretes, de még mindíg nem látok olyan állítást és annak bizonyítását, ami garantálná, hogy a végeredményül adódó kiterítésben nem lehet átfedés. Például: "P átforgatásakor az újonnan S-re érkező P csúcsok benne vannak a vetület megfelelő, esetleg összehúzásokkal már módosított tartományában". E'' jelöletlen szomszédját G'' -vel jelölve az összehúzás során mi lesz az E''G'' ívből? Egyenes szakasz? Vagy ha körív, akkor mekkora sugarú?
|
| Előzmény: [1622] bily71, 2012-12-26 23:24:30 |
|
| [1622] bily71 | 2012-12-26 23:24:30 |
 "Nem elemeztem a bizonyítást betűről betűre, de első ötletem az, nézd meg, mennyire igazak az összehúzásról elmondottak arra az Li'' lapra, melynek eredetijét, P poliéder Li lapját, az O1O2 szakasz átdöfi."
Átnéztem és átgondoltam. Az F fának a következő feltételeknek kell eleget tennie (F-et az egyszerűség kedvéért rajzolhatjuk közvetlenül P-re is).
(i) Az Li lapra (melyet az O1O2 egyenes döf) illeszkedő csúcs levél.
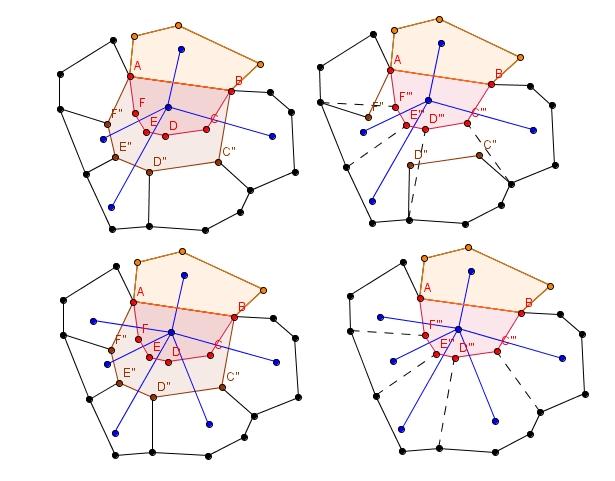
(ii) Létezik F1, F2, ..., Fm fa gráf sorozat úgy, hogy F1 egyetlen, az S síkkal párhuzamos L1 lapra illeszkedő csúcsból áll (ez legyen F gyökere), 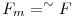 , továbbá Fk+1 úgy nyerjük Fk-ból, hogy kiválasztjuk Fk egy levelét (vagyis egy lapot, melyre Fk egy levele illeszkedik), majd összekötjük az összes olyan szomszédos lapra illeszkedő csúccsal, mely nem csúcsa Fk-nak. , továbbá Fk+1 úgy nyerjük Fk-ból, hogy kiválasztjuk Fk egy levelét (vagyis egy lapot, melyre Fk egy levele illeszkedik), majd összekötjük az összes olyan szomszédos lapra illeszkedő csúccsal, mely nem csúcsa Fk-nak.
Az ábrán (mely csak egy elképzelt esetet ábrázol) azt láthatjuk, mikor P-t átforgatjuk az AB élen, és az ABC''D''E''F'' lapot ráhúzzuk ABCDEF lapra. Az ábra felső részén látható, hogy ha nem (ii) szerint építjük fel F-et, akkor az összehúzás közben bár a összehúzott lap nem fed át egy lapot sem, de a megnyúlt szomszédainál felléphet átfedés, és nem tudhatjuk, hogy az megszűnik-e.
Az alsó részen módosítottuk F-et (ii) szerint, így a megnyúlt lapoknál sem lép fel átfedés. Most már kimondhatjuk, hogy az előbbi feltételeknek eleget tevő F szerint kiterítve P-t nem lép fel átfedés, és pont ezt akartuk megmutatni.
Amúgy kellemes ünnepeket! :)
|
 |
| Előzmény: [1620] HoA, 2012-12-23 16:24:41 |
|
| [1621] bily71 | 2012-12-23 20:44:42 |
 Igen, (ezt a "bizonyítást" a közzététel előtti álmatlan éjszakámon ötlöttem ki, csak úgy eszembe jutott) azon már a legelején gondolkoztam, hogy a "felső", vagyis az Li' lapot, amelyiket az O1O2 szakasz átdöfi, nem kellene hozzávenni a fához (ami így nem is, vagy hiányos feszítőfa), hanem utána biggyesztenénk oda az F* hiányos feszítőfa valamelyik levele után (de melyik után?), ugyanis ennek képe Li'' nem korlátos, nem világos, hogy mi történik vele az összehúzás közben, de később annyira nyilvánvalónak tűnt minden, hogy nem foglalkoztam vele.
Azonban úgy tűnik, hogy ha az Li'' nélküli sokszögre alkalmazzuk az összehúzást, akkor nem kapunk átfedést, még átgondolom, de annyira egyértelműnek tűnik.
|
| Előzmény: [1620] HoA, 2012-12-23 16:24:41 |
|
| [1620] HoA | 2012-12-23 16:24:41 |
 Én nem tudok, mivel eddig sohasem foglalkoztam ezzel a problémával, csak felszólításodra néztem bele. A "Dürer sejtés" Wikipedia oldalán azonban látható ez a hivatkozás:
http://www.ams.org/samplings/feature-column/fcarc-nets
Ebben megtalálhatod az alja felé a két következő idézetet:
"Her work related to finding a way of generating random 3-dimensional convex polyhedra and then choosing a random unfolding (not such simple issues) and seeing if the random unfolding overlapped. Her results showed that as the number of vertices of the solid increased, for a fixed specific solid the number of unfoldings where an overlap did occur increased" . ( Amiből itt csak az az érdekes, hogy növekvő csúcsszámmal növekszik azoknak a kiterítéseknek a száma, ahol átfedés van. ) És
"...no matter what reasonable type of tree Schlickenrieder picked, he was able to find examples of 3-dimensional convex solids where this tree did not lead to a net unfolding without overlaps." ( vagyis adott típusú fákat vizsgálva Sch.-nak sikerült olyan fát találni, mely nem vezetett átfedés nélküli kiterítésre )
A lényeg: A sejtés konvex poliéderekre sem azt mondja, hogy minden kiterítés átfedésmentes, hanem csak azt, hogy létezik átfedésmentes kiterítés. A Wikipédia cikk szerint "Dürer sejtette, hogy minden poliédert fel lehet vágni az élei mentén úgy, hogy lapjai (átfedés nélkül) kiteríthetőek legyenek a síkban, egy összefüggő sokszöget képezve." - és nem azt, hogy minden kiterítés ilyen.
Mivel te F megválasztására semmilyen különleges feltételt nem adtál meg, módszered az említett átfedéses kiterítéseket is létrehozná, tehát valahol a bizonyításban lehet a hiba. Nem elemeztem a bizonyítást betűről betűre, de első ötletem az, nézd meg, mennyire igazak az összehúzásról elmondottak arra az Li'' lapra, melynek eredetijét, P poliéder Li lapját, az O1O2 szakasz átdöfi.
|
| Előzmény: [1619] bily71, 2012-12-23 15:31:46 |
|
| [1619] bily71 | 2012-12-23 15:31:46 |
 Persze, hogy nem látod, mert a két sokszög ugyanaz. A különbség az út, hogy hogyan jutunk a sokszögig. Közvetlenül is felrajzolhatjuk H-t és F-et, majd szétvághatjuk, de attól még nem tudjuk, hogy lesz-e átfedés. Mutattam egy utat, ahol úgy kapjuk meg a sokszöget, hogy egyik lépésben sem keletkezik átfedés. Tulajdonképp azt próbálom demonstrálni, hogy H bármely F feszítőfája jó.
Most azért elbizonytalanítottál. Létezik olyan F, hogy a szétvágás és kiterítés során átfedést kapunk? Ha megkérlek, mutatnál erre példát?
|
| Előzmény: [1618] HoA, 2012-12-23 00:40:02 |
|
| [1618] HoA | 2012-12-23 00:40:02 |
 Nem látom, mi a különbség a módszereddel kapott síkbeli sokszög és aközött, hogy H-t - és így F-et - közvetlenül P-re rajzoljuk és P-t felvágjuk az F élei által nem metszett poliéder élek mentén. Vagyis kérlek mutass egy példát arra, ahol a két eredményül kapott sokszög különböző. Mert ha a két sokszög ugyanaz, akkor...
|
| Előzmény: [1616] bily71, 2012-12-21 22:42:34 |
|
| [1617] bily71 | 2012-12-22 23:07:33 |
 Azért több érdeklődést vártam. Ha jól tudom, a Dürer-sejtés még nyitott, Bezdek Dániel csak speciális estben bizonyította. Ha az előbbi megoldás jó, akkor én a poliéderek bővebb halmazán bizonyítottam.
Készítettem egy ábrát, melyen két dimenziós metszetben P egy lapjára illeszkedő szakaszon mutatom be, hogy mit is csináltunk P-vel. Az AB szakaszt O1-ből G1 körre vetítjük, majd a kapott A'B' körívet O2-ből S-re invertáljuk, így kapjuk az A''B'' szakaszt. Ezek után eltoljuk AB-t 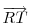 vektorral, kapjuk A1B1 szakaszt. Az A''B'' szakaszt ráhúzzuk A1B1-re, így kapjuk az A'''B''' szakaszt. Az AB és az A'''B''' szakaszok egybevágók. vektorral, kapjuk A1B1 szakaszt. Az A''B'' szakaszt ráhúzzuk A1B1-re, így kapjuk az A'''B''' szakaszt. Az AB és az A'''B''' szakaszok egybevágók.
Az A''B'' szakasz mindig nagyobb, mint az AB. Ugyanígy, mikor P-t görgetjük (elforgatjuk az éle, mint tengely körül), a görgetett lap mindig része a második képének, tehát összehúzást kell alkalmaznunk, hogy a harmadik kép egybevágó legyen az eredetivel. Az összehúzás során az átvágott élek mentén a szomszédos lapok eltávolodnak, vagyis rés keletkezik a síkon, így nem keletkezhet átfedés, a nem átvágott élek mentén pedig a szomszédos lap megnyúlik az összehúzás irányában, de átfedés itt sem keletkezik. Szemléletesen az történik, hogy felszabdaljuk az S síkot, majd az összehúzás transzformációval a síkrészeket ráhúzzuk P lapjaira, vagyis az egész S síkot ráképezzük P-re. (Ez nem egy szokványos transzformáció, hiszen két összehúzás között P-t ide-oda mozgatjuk.) Ez lenne a levezetés lényege. Kíváncsian várom a véleményeket.
|
 |
| Előzmény: [1616] bily71, 2012-12-21 22:42:34 |
|
| [1616] bily71 | 2012-12-21 22:42:34 |
 183. feladat. Adott P 3 dimenziós konvex poliéder. Terítsük ki P lapjait a síkba úgy, hogy átfedés nélkül egy összefüggő sokszöget alkossanak, azaz adjuk meg P egy hálóját!
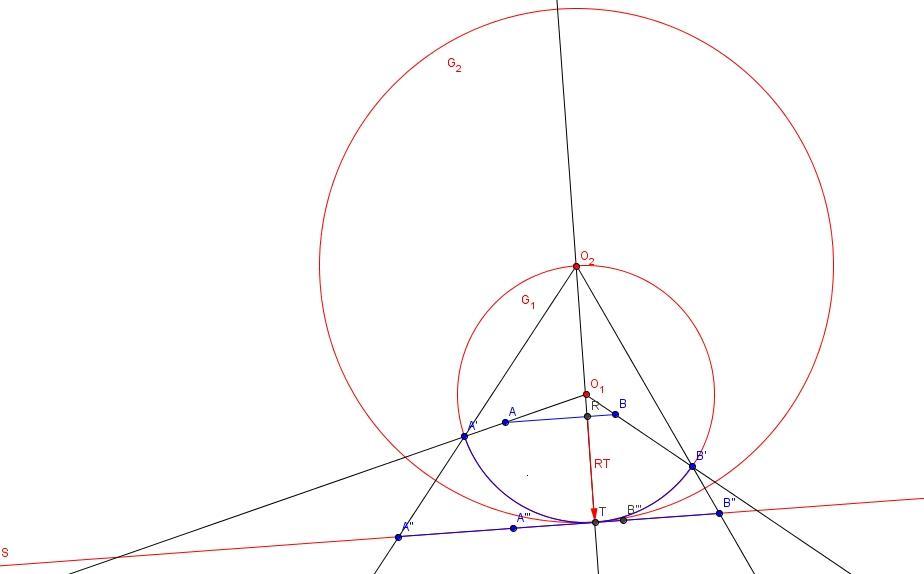
Megoldás. Helyezzük P-t egy 3 dimenziós G1 gömbbe úgy, hogy az O1 gömb középpont P egy belső pontja legyen, továbbá P minden pontja G1 belső pontja legyen! Vetítsük P-t O1-ból G1 felszínére úgy, hogy ha Q pont P egy élének egy pontja, akkor Q' pont az O1Q egyenes és G1 felszínének metszete! Ekkor egy gömbre rajzolt P' gráfot kapunk.
Válasszuk ki P' minden lapjának egy belső pontját, (azaz a P' gömbre rajzolt gráf körei által határolt gömbfelszín tartományok egy belső pontját), majd kössük össze ezeket, ha két szomszédos lap, (azaz közös éllel rendelkező lapok) belső pontjai! Ekkor egy H gráfot kapunk. Legyen F H egy feszítő fája!
Sztereografikus projekciót alkalmazva képezzük P'-t és F-et az S síkra! S párhuzamos P egy lapjával, T pontban érinti érinti G1-et, ugyanitt érinti G2-t, az inverzió gömbjét, melynek O2 középpontja T átellenes pontja G1-en, továbbá O2 nem csúcsa P'-nek és F-nek, és nem illeszkedik P' és F egyik élére sem. Ekkor egy síkba rajzolt P'' gráfot és egy F' fát kapunk.
Legyen az R pont P, az S síkkal párhuzamos, L1 lapja és az O1T egyenes metszete! Toljuk el P-t az 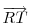 vektorral! Ekkor L1 eltolt képe illeszkedik S-re. vektorral! Ekkor L1 eltolt képe illeszkedik S-re.
Gondoljunk S-re úgy, mint vastagság nélküli rugalmas, vágható anyagból álló felületre! Vágjuk át S-t azon élek mentén, melyeket nem metsz F' egyik éle sem!
Legyen az L1 lap egy csúcsa V1, húzzuk bele V1''-t V1-be! Ismételjük ezt L1'' minden csúcsával! Az "összehúzás" transzformáció után L1'' képe egybevágó lesz L1-gyel, hisz fedik egymást.
Gördítsük át az eltolt P-t az egyik élén az S síkon az F' fa egy éle mentén, vagyis P egy olyan élén, mely metszi F' egy élét. Ekkor az L2 lap illeszkedik S-re, úgy, hogy az L1,L2 lapok közös éle fedi az összehúzott L1'' és a félig összehúzott L2'' lapok közös élét, továbbá L2 része L2''-nek. Legyen V2 az L2 lap egy csúcsa! Húzzuk bele V2''-t V2-be! Ismételjük ezt L2'' minden csúcsával! Az összehúzás után L2'' képe fedi L-2-t, így azok egybevágók. Az összehúzott L1'',L2'' lapok nem fedik át egymást. Az összehúzott L2'' nem fedi át egyik vele szomszédos másik lapot sem, hiszen vagy át van vágva az S sík a közös él mentén, így inkább távolodott szomszédjától, mivel az helyben maradt, vagy a közös élt metszi F'-et, ekkor nem keletkezik átfedés.
Gördítsük végig P-t F' minden útján az utak valamilyen sorrendjében! Egy út végére érve gördítsük visszafelé az úton P-t, míg az L1 lap nem illeszkedik újra S-re! Minden gördítés során alkalmazzuk az összehúzás transzformációt!
F' minden útját végigjárva egy összefüggő sokszöget kapunk, mely sokszög P lapjaival egybevágó sokszögekből áll, így a sokszög területe és P felszíne egyenlő, vagyis eleve kizárt, hogy a gördítések során átfedés keletkezett. Az S sík átvágása miatt az összehúzás során megkettőződött éleket újból fedésbe hozva P-vel egybevágó poliédert kapunk (a sokszögből visszahajtogathatjuk P-t), vagyis a feladatot sikerült megoldanunk.
P tetszőleges volt, ezért a feladatot megoldva egyúttal konstruktív bizonyítást adtunk Dürer sejtésére abban az esetben, ha a poliéder konvex.
Boldog Világvégét! :)
|
|
| [1615] w | 2012-12-12 17:59:04 |
 Ez is szép megoldás.
A feladat bemutatja, hogy több ismerettel sokkal bonyolultabban oldanánk meg egy nem nyilvánvaló általános iskolás feladatot, mint egy korlátos ismerettel rendelkező nyolcadikos. (Persze az más kérdés, hogy egy általános iskolás mit tesz, ha egy trigonometrikus egyenletet kellene fejtegetni.) Akinek elemi geometriával van dolga, annak állandó gyakorlásra van szüksége, hogy ezekhez való érzékét fenntartsa. (Megjegyzendő, hogy mindenhol van kivétel.)
A feladat megoldása:
Célszerű az egyenlő szárúságot kihasználni. Rajzoljuk be a háromszög szimmetriatengelyét, ez messe CP-t Q-ban, ekkor QAC<=ACQ<=30°. Vegyük észre, hogy AP felezi a BAQ<-et, ráadásul PQ az AQB< felezője. Így P az AQB háromszög beírt körének középpontja, azaz BP felezi ABQ<-et. BPC<=180°-(80°/2+80°/4)-(50°-30°)=100°.
Ez egyszerű volt. Kis túlzással annyi kellett hozzá, hogy észrevesszük, hogy az egyenlő szárú háromszög szimmetrikus. Aki erre rákényszerítené a szabályos 18-szöget, az azért teszi, mert a feladatot ennél összetettebbnek képzeli, és jogosan. Tehát ajánlom a feladatok egyszerű megközelítését (aki elolvasta a bemutatkozásomat, az el is várhatja a könnyebb példákat :).
Megint más kérdés, hogy milyen a feladat általánosítása...
|
 |
| Előzmény: [1614] HoA, 2012-12-11 13:07:32 |
|
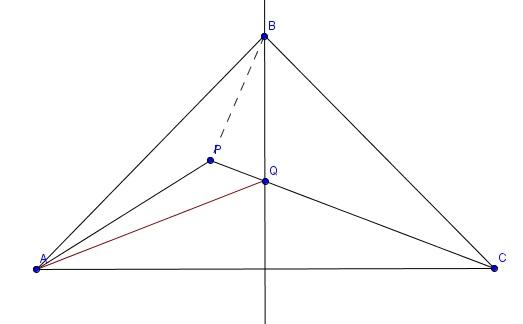
| [1614] HoA | 2012-12-11 13:07:32 |
 Hogy mennyire tömény és elegáns, azt ítélje meg más, minden esetre "nyolcadikosabb" , mint az előző.
Építsük fel a mellékelt ábrát az ABC háromszög csúcsaiból, a körülírt kör O középpontjából és a CA oldallal 30 fokos szöget bezáró CE egyenesből kiindulva. CO felező merőlegesének és CE -nek a metszéspontja Q. Az állandó QC hosszúságú piros szakaszok ismételt felméregetésével kialakul az ábra. A 10, 20, 40 ill. 60 fokos szögeket kékkel, rózsaszínnel, lilával ill. zölddel jelöltem. Látható - és persze bizonyítható - , hogy P a feladatban definiált pont.
A BPC háromszöget O körül pozitív irányban 100 fokkal elforgatva P Q-ba , B C-be kerül, A BP szakasz képe tehát a PC-vel egy egyenesbe eső CQ, ezért BPC szög 100 fok.
|
 |
| Előzmény: [1611] w, 2012-12-10 16:46:48 |
|
| [1613] w | 2012-12-10 22:22:18 |
 Jogos a hozzászólásod. Én arra gondoltam, hogy a feladatot úgy is meg lehet oldani, hogy csak a következőket használhatjuk: háromszög belsőszög-összege, nevezetes vonalai, beírt kör, szög/szakasz/pont felvétele.
A Fálesz-HoA-megoldás sokkal hasznosabb, mint az, amire gondolok. Mindenesetre hamarosan - amint lesz időm az ábrát elkészíteni - közlöm a megoldásomat.
******
Mutassuk meg, hogy ha egy háromszög két belső szögfelezője azonos hosszú, akkor és csak akkor a háromszög egyenlő szárú.
|
| Előzmény: [1612] Lóczi Lajos, 2012-12-10 18:30:06 |
|
|
| [1611] w | 2012-12-10 16:46:48 |
 Köszönöm szépen, a megoldásotok nagyon szép, és igen sok feladatra felhasználható.
A feladatot eredetileg nyolcadik osztályosoknak tűzték ki, talán 2007-ben (?), ezért nyilván van olyan megoldás, ami tömény, elegáns háromszöggeometria.
|
| Előzmény: [1610] HoA, 2012-12-10 11:26:43 |
|
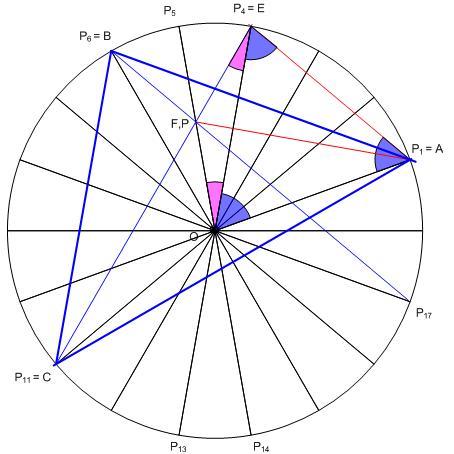
| [1610] HoA | 2012-12-10 11:26:43 |
 A [1609] –beli megközelítés egy konkrét megvalósítása, a szükséges nem triviális közös metszéspont bizonyításával: Válasszuk meg az A, B, C csúcsokat az ábra szerint, így ABC a feladatban szereplő háromszög. Mivel egy sokszög oldalhoz, ill. a körülírt körben a hozzá tartozó ívhez 10 fokos kerületi és 20 fokos középponti szög tartozik, AOC  = 160 fok , így CAO = 160 fok , így CAO  = 10 fok. A CA –val 30 fokos szöget bezáró P11P4 ( = CE ) , egyenes és a P5P14 átmérő metszéspontja legyen F. Az OEF háromszögben OEF = 10 fok. A CA –val 30 fokos szöget bezáró P11P4 ( = CE ) , egyenes és a P5P14 átmérő metszéspontja legyen F. Az OEF háromszögben OEF  = 20 fok, mint a P11P13 ívhez tartozó kerületi szög, FOE = 20 fok, mint a P11P13 ívhez tartozó kerületi szög, FOE  = 20 fok, mint a P4P5 –höz tartozó középponti szög, OEF háromszög egyenlőszárú. Az AOE egyenlőszárú háromszögben O-nál 60 fokos szög van, mint P1P4 –hez tartozó középponti szög, AOE háromszög szabályos. AEFO deltoid, AF átlója felezi a 60 fokos OAE szöget, FAO = 20 fok, mint a P4P5 –höz tartozó középponti szög, OEF háromszög egyenlőszárú. Az AOE egyenlőszárú háromszögben O-nál 60 fokos szög van, mint P1P4 –hez tartozó középponti szög, AOE háromszög szabályos. AEFO deltoid, AF átlója felezi a 60 fokos OAE szöget, FAO  = 30 fok, FAC = 30 fok, FAC  = 40 fok , F tehát feladatunk P pontja. Mivel P rajta van a P5P14 átmérőn és a P11P4 átlón, ezért az utóbbinak P5P14 –re vett tükörképén , a P6P17 átlón is rajta van. A BCP háromszögben BCP = 40 fok , F tehát feladatunk P pontja. Mivel P rajta van a P5P14 átmérőn és a P11P4 átlón, ezért az utóbbinak P5P14 –re vett tükörképén , a P6P17 átlón is rajta van. A BCP háromszögben BCP  = P6CP4 = P6CP4 = 20 fok, CBP = 20 fok, CBP  = P11BP17 = P11BP17 = 60 fok, így BPC = 60 fok, így BPC  = 100 fok. = 100 fok.
|
 |
| Előzmény: [1609] Fálesz Mihály, 2012-12-10 09:28:23 |
|
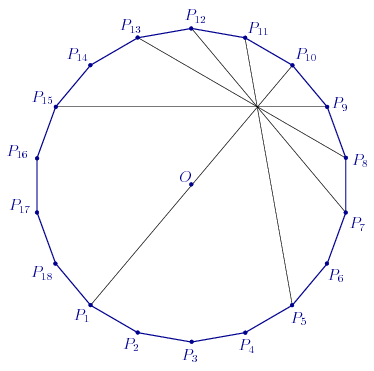
| [1609] Fálesz Mihály | 2012-12-10 09:28:23 |
 Az ilyenfajta feladatokhoz egy kiváló cikk: Csirmaz László: Egy geometriai feladatról
A lényeg röviden:
1. Egy szabályos 18-szögben az átlók közötti szögek mind a 10o többszörösei.
2. Vannak olyan átlók, amik nem teljesen triviálisan egy ponton mennek át. Például a O középpontú P1P2...P18 szabályos 18-szögben a P9P15 átló az OP12 sugár felező merőlegese, és ebből következik, hogy a P1P10 egyenes tükörképe a P9P15 átlóra éppen a P7P12 egyenes. Ha ezeket a P1P10 átmérőre is tükrözzük, láthatjuk, hogy a P1P10, P5P11, P7P12. P8P13 és P9P15 átlók egy ponton mennek át.
3. A feladat megoldása ezek után abból áll, hogy megkeressük a rengeteg oldal és átló között a feladat ábráját...
|
 |
| Előzmény: [1608] w, 2012-12-09 11:22:59 |
|
|
|
| [1606] w | 2012-12-08 21:34:35 |
 ABC háromszögben AB=AC, P belső pontra PAC<=40 fok, ACP<=30 fok. Mekkora a BPC<, ha ABC<=80 fok?
|
|
|
|
| [1603] Mordon | 2012-10-31 15:00:07 |
 P az ABC háromszög belső pontja. A CP egyenes az AB oldalt a D, az AP egyenes a BC oldalt az E, a BP egyenes a CA oldalt az F pontban metszi. Tudjuk, hogy PA+PB+PC=43 és PD=PE=PF=3. Határozzuk meg a PA.PB.PC szorzat értékét.
Ennek a tavalyi Szőkefalvi feladatnak a megoldását valaki le tudná írni?
Előre is köszönöm!
|
|
|
| [1601] HoA | 2012-10-24 13:02:31 |
 Gondolom mivel a szereplő betük közül N a B mellett van a billentyűzeten, a kérdező B-t gondolt. Ekkor a metszéspont Jónás T pontja, a keresett hosszúságok AT = 4/5 AC = 4/5 * 28 cm = 22.4 cm, BT = 3/5 BC = 3/5 * 21 cm = 12.6 cm , mint [1597]-ben.
|
| Előzmény: [1596] jonas, 2012-10-23 22:01:37 |
|
|
| [1599] Blinki Bill | 2012-10-24 06:57:11 |
 Mivel F felezi az ívet, ezért CF a C-nél levő szög szögfelezője és az AB oldalt a szomszédos oldalak arányában osztja a szögfelező-tétel miatt. Az arány 3:4, így a 35cm-t kell ilyen arányban bontani, adódik 20cm és 15cm.
|
| Előzmény: [1595] Kásás János, 2012-10-23 20:10:04 |
|
|
| [1597] jonas | 2012-10-23 22:26:48 |
 A feladat első részéhez vedd észre, hogy a háromszög derékszögű.
Tegyük fel, hogy a BC oldal hossza 21 cm, az AC oldalé pedig 28 cm. Koordinátázzuk úgy a síkot, hogy a háromszög körülírt körének a középpontja legyen az origó, az A pont legyen a (-17.5 cm, 0), a B legyen (17.5 cm, 0), a C második koordinátája pedig legyen pozitív.
Jelölje T a C-hoz tartozó magasság talppontját. A talppont az AB átfogón úgy helyezkedik el, hogy az AT távolság egyenlő az AC befogó négyzete osztva az átfogóval, vagyis 22.4 cm. Ebből a T koordinátái (4.9 cm, 0). A CT magasság hossza egyenlő a befogók szorzata osztva az átfogóval, vagyis 16.8 cm, így a C koorindátája (4.9 cm, 16.8 cm).
Mármost az F pont a feladat szerint annak az ívnek a felezőpontja, aminek az átmérője az A és a B pont, ezért az F koordinátái (0, -17.5 cm). Ebből a CF szakasz metszete az AB koordinátatengellyel, amit hívjunk R-nek, (4.9cm.17.5cm/(17.5cm+16.8cm),0) = (-2.5cm,0). Ebből pedig az AR szakasz hossza 20 cm, az RB szakasz hossza pedig 15 cm.
|
| Előzmény: [1595] Kásás János, 2012-10-23 20:10:04 |
|
|
| [1595] Kásás János | 2012-10-23 20:10:04 |
 Segítséget szeretnék kérni tőletek, mert nem tudom megoldani a gyermekem házi feladatát:
Az ABC háromszög oldalainak hossza 21, 28 és 35 cm. A háromszög köré írt kört a háromszög csúcsai három ívre bontják. Ezek közül a leghosszabb ív felezőpontja F. Kössük össze F-et a háromszög szemközti csúcsával (legyen ez a csúcs C). Mekkora részre bontja a CF szakasz az AB szakaszt? Tükrözzük a C pontot az AN szakasz egyenesére (C’). Mekkora részre bontja a CC’ szakasz az AB oldalt?
A szögfüggvényeket még nem tanulták, azokat nem lehet használni.
Fáradozásotokat előre is megköszönve.
Tisztelettel: Kásás János
|
|
|
| [1593] m2mm | 2012-08-14 10:50:14 |
 Projektív megoldást találtam én is, elemi engem is érdekelne.
Ma böngészve régebbi KöMaL-példák között találtam a B.3680. feladatra, ami tulajdonképpen a 181. feladat nemtriviális része, így egy újabb megoldást rakhatunk a feladathoz, a hivatkozásban láthatunk egy újabb bizonyítást.
B.3680
|
| Előzmény: [1570] Vonka Vilmos Úr, 2012-05-27 20:25:16 |
|
|
|
|
|
| [1588] Fálesz Mihály | 2012-08-13 09:07:23 |
 Állandó görbületű felületeken (terekben) is igaz, hogy ha AB egy kör (gömb) átmérője, C pedig egy harmadik pont a körvonalon (gömbfelületen), akkor az ABC háromszög C-nél levő szöge egyenlő a másik két csúcsnál levő szög összegével.
|
| Előzmény: [1587] Gézoo, 2012-08-13 08:23:50 |
|
| [1587] Gézoo | 2012-08-13 08:23:50 |
 Ez nyilvánvaló. Alapból a  szimbólum a kör kerületének és átmérőjének arányát jelöli. Az Eukledeszi geometria mint elvi felvetés, kizárólag olyan alakzatokra érvényes amelyek "közelében" ( azaz végtelen nagy távolságon belül) nincs anyag amely "deformálná" a téridőt. Vagyis a világmindenségben sehol sem érvényes, mert nincs olyan térrész ahol ne lenne téridő görbület. Ebből következően, a valós testek, "síkidomok" esetében a Pi értéke, még elvileg sem lehet állandó. szimbólum a kör kerületének és átmérőjének arányát jelöli. Az Eukledeszi geometria mint elvi felvetés, kizárólag olyan alakzatokra érvényes amelyek "közelében" ( azaz végtelen nagy távolságon belül) nincs anyag amely "deformálná" a téridőt. Vagyis a világmindenségben sehol sem érvényes, mert nincs olyan térrész ahol ne lenne téridő görbület. Ebből következően, a valós testek, "síkidomok" esetében a Pi értéke, még elvileg sem lehet állandó.
Egy példával: "Ha például az asztalon felállítunk három darab gúlát és a csúcsaikat összekötő síkról azt feltételezzük, hogy az valóban sík, akkor tévedünk, mert a téridő görbületet nem vettük figyelembe. Azaz mi a képzeletünkben hiába egy síkot ültetünk a három csúcsra, a csúcsokat érintő 2D-s felszín az domború. Egészen pontos legyek, a fel-le irány figyelembe vételével, akkor homorú. Mégpedig egy parabolikus forgásfelület. (Forgási paraboloid.)
Azaz ha ezen paraboloidon lenne egy kör átmérője (vagy egy gömb átmérőjén átmenő 2D-s felülete) akkor a kör alsó feléhez hajló átmérő hossza, nagyobb mint az alsó fél hossza/Pi/2 azaz ha a hosszok aránya (a definíció szerint ) adja a Pi értékét, akkor a Pi kizárólag csak a nem létező síkok esetében állandó értékű."
Viszont ez nem jelenti azt, hogy például Thales tételének általánosított formája ne lehetne érvényes a görbült terek alakzatai közül némelyekre.
Vagyis a kérdés, feltételezhető-e olyan alakzatok léte amelyekre érvényes Thales tétele.
|
| Előzmény: [1586] Lóczi Lajos, 2012-08-11 22:05:20 |
|
|
| [1585] Gézoo | 2012-08-11 17:59:04 |
 "Megkérlek, mondd ki Thálesz tételét abban az alakban, ami a szívedhez legközelebb áll. "
Továbbra sem érted a kérdést, felteszem más formában:
Olyan alakzatok közül amelyekben a  értéke eltér az elvi síkon érvényes 3,14... értéktől, akadhat-e olyan amelyre érvényes lehet Thales tétele? értéke eltér az elvi síkon érvényes 3,14... értéktől, akadhat-e olyan amelyre érvényes lehet Thales tétele?
|
| Előzmény: [1581] Kemény Legény, 2012-08-05 10:49:11 |
|
|
| [1583] Kemény Legény | 2012-08-05 13:29:31 |
 A kérdés általánosan megválaszolható gráfelméleti úton, Euler poliéder-tételének felhasználásával, de adható egyszerű megoldás szögszámolással is.
Legyen a "külső" sokszög k0 csúcsú, továbbá legyenek "kivágva" belőle k1,...kn csúcsú sokszögek, azaz n db "lyuka" legyen a "fánknak". Továbbá tekintsünk egy háromszögelését a "fánknak" N db háromszöggel.
Először is felhasználjuk, hogy egy "lyuk" nélküli k-szög belső szögeinek összege=(k-2)*180°. /Erre később visszatérünk./
Ezután adjuk össze az összes háromszögben megjelenő szöget és adjuk hozzá a "lyukakat" alkotó sokszögek szögeit is: N*180°+(k1-2)*180°+...+(kn-2)*180° lesz az összeg.
Ezt az összeget azonban másként is megkaphatjuk: minden belső pont (összesen k1+...+kn darab) körüli 360°-os szöget és a külső sokszög belső szögeit összeadva épp ezt kapjuk, azaz:
N*180°+(k1-2)*180°+...+(kn-2)*180°=(k1+...+kn)*360°+(k0-2)*180°
Azaz N=2n-2+k0+k1+...+kn háromszög szerepel a felbontásban minden esetben. Ez összhangban van a tapasztalataiddal, ugyanis csúcsok száma=k0+k1...+kn. Tehát háromszögek száma=csúcsok száma + 2*lyukak száma -2.
Visszatérve az elejére, még be kellene látni, hogy minden nem lyukas sokszög szögeinek összege (k-2)*180°. Ez nem egy triviális állítás, sőt impliciten feltételeztük, hogy mindig létezik egyáltalán háromszögelés. Ha belegondolsz, nem is olyan egyszerű belátni, hogy minden sokszög háromszögelhető. Ha ugyanis tudjuk, hogy van háromszögelés, akkor belátható (gondold végig, miért), hogy található olyan háromszög, aminek a csúcsait 3 szomszédos csúcs adja, a háromszöget elhagyva pedig alkalmazható a teljes indukció.
A vége kicsit vázlatosra sikerült, de érdemes végiggondolni, miért is igazak a fentiek és hogyan megy ez precízen.
|
| Előzmény: [1582] cocka, 2012-08-05 12:51:53 |
|
| [1582] cocka | 2012-08-05 12:51:53 |
 Sziasztok!
Nos nekem az lenne a kérdésem, hogy hogy lehet meghatározni hogy egy tetszőleges (pl. akár konkáv vagy fánkszerű) sokszög hány háromszögre bontható?
Rajzolgattam a Geogebrában és ilyenek jöttek ki:
geogebra példák
Annyit vettem észre, hogy ha fánkszerű az alakzat, akkor a kiindulási sokszög csúcsainak száma megegyezik azzal, ahány háromszögre az alakzat bontható.
Ha viszont nem fánkszerű, akkor a kiindulási sokszög csúcsainak száma -2 db háromszögre bontható.
Mitől függ ez? Van erre valami általános képlet amivel kiszámolható hogy egy-egy ilyen általános sokszög hány háromszögre bontható?
Másrészt nem vizsgáltam, de lehet akár egynél több üreg is a fánkszerű alakzatokban.
Köszönöm, ha válaszoltok.
|
|
| [1581] Kemény Legény | 2012-08-05 10:49:11 |
 Megkérlek, mondd ki Thálesz tételét abban az alakban, ami a szívedhez legközelebb áll. Miután megtetted, mondd meg, melyik, a tételben szereplő "alakzatot" szeretnéd általánosabbra cserélni.
Én megtettem. Kimondtam a tételt, majd utána annak egy általánosítását is. Az eredeti tételben levő "derékszög" és "körvonal" fogalmakat általánosabbra: "adott szög"-re és "két körív"-re cseréltem.
Tehát megismétlem a kérésem: mondd ki egy formájában a tételt, és jelezd, melyik pontján szeretnél általánosítani.
|
| Előzmény: [1580] Gézoo, 2012-08-05 10:21:59 |
|
| [1580] Gézoo | 2012-08-05 10:21:59 |
 "Mi lenne, ha a matematikai jellegű topikokban nem homályos kérdéseket tennél fel, hanem elmondanád, mire is gondolsz? "
Mi ezen ami számodra homályos?
"Thales tételét még milyen alakzatokra alkalmazhatnánk úgy, hogy érvényes maradjon?"
|
| Előzmény: [1579] Kemény Legény, 2012-08-04 18:41:49 |
|
| [1579] Kemény Legény | 2012-08-04 18:41:49 |
 Mi lenne, ha a matematikai jellegű topikokban nem homályos kérdéseket tennél fel, hanem elmondanád, mire is gondolsz?
Itt nincs helye mellébeszélésnek, mint az "Einstein tévedett"-jellegű parttalan vitáknak. Mondj ki egy állítást világosan, mit is szeretnél és hogyan általánosítani?
Hogy konstruktívabb legyek: Thálesz tétele (egyik megfogalmazásában) azt mondja ki, hogy azon pontok mértani helye, amelyekből egy adott szakasz derékszögben látszik, éppen a szakaszra mint átmérőre írt körvonal lesz.
Ennek általánosítása pl. a középponti-kerületi szögek tétele, ami (többek között) azt mondja, hogy azon pontok helye, amiből egy adott szakasz adott szögben látszik, két körív lesz, melyek a szakaszra szimmetrikusan helyezkednek el.
|
| Előzmény: [1578] Gézoo, 2012-08-04 18:05:51 |
|
|
| [1577] Hajba Károly | 2012-08-03 20:12:55 |
 Valószínűleg a Pitagorasz-tételre gondolsz. Elvileg minden síkbeli alakzatra igaz, ha nagyítással ill. elfogatással/eltolással egymásba transzformálhatóak. Pl. ezen tényből következik a Hippokratész holdacskáinak helyessége is.
|
| Előzmény: [1576] Gézoo, 2012-08-03 17:19:25 |
|
| [1576] Gézoo | 2012-08-03 17:19:25 |
 Bocs, hogy lustaságból hozzád fordulok a kérdéssel, de felmerült bennem az, hogy Thales tételét még milyen alakzatokra alkalmazhatnánk úgy, hogy érvényes maradjon?
Tudnál ebben segíteni?
Persze természetesen, mindenki más segítségét is megköszönöm!
Más is elmondhatja az érveit a kérdésről!
|
| Előzmény: [1574] Fálesz Mihály, 2012-07-14 15:57:42 |
|
|
| [1574] Fálesz Mihály | 2012-07-14 15:57:42 |
 182. feladat (az idei olimpia 5. feladata, javasolta: Josef Tkadlec, Csehország).
Legyen az ABC háromszögben BCA =90o, és legyen D a C-ből induló magasságvonal talppontja. Legyen X a CD szakasz belső pontja. Legyen K az AX szakasznak az a pontja, amire BK=BC. Hasonlóan, legyen L a BX szakasznak az a pontja, amire AL=AC. Legyen M az AL és BK egyenesek metszéspontja. =90o, és legyen D a C-ből induló magasságvonal talppontja. Legyen X a CD szakasz belső pontja. Legyen K az AX szakasznak az a pontja, amire BK=BC. Hasonlóan, legyen L a BX szakasznak az a pontja, amire AL=AC. Legyen M az AL és BK egyenesek metszéspontja.
Bizonyítsuk be, hogy MK=ML.
Szerintem ez volt az olimpia legviccesebb feladata.
|
|
|
| [1572] sakkmath | 2012-07-03 23:49:10 |
 A Grinberg-cikk 4. oldalának 4. ábrája alapján írjuk fel az általánosított Ptolemaiosz-tételt az egységsugarú kör köré írt ABCD érintőnégyszögre.
Ekkor a cikk 24. oldalának 14. tételében speciálisan  =1. Ezzel előáll az A.536. feladat kiindulási feltétele, s így e feladat érdekes geometriai megközelítését kapjuk. Erre utaltam a Lejárt határidejű KÖMAL feladatokról/[685]-ös hsz-ben. Az akkor említett "elakadáson" hamar túljutottam :-) =1. Ezzel előáll az A.536. feladat kiindulási feltétele, s így e feladat érdekes geometriai megközelítését kapjuk. Erre utaltam a Lejárt határidejű KÖMAL feladatokról/[685]-ös hsz-ben. Az akkor említett "elakadáson" hamar túljutottam :-)
|
| Előzmény: [1566] sakkmath, 2012-05-25 22:06:36 |
|
| [1571] HoA | 2012-05-27 20:42:54 |
 Az egyik irány elemi geometriai bizonyítása triviális. Mivel az átlók által bezárt szomszédos szögek összege 180o, a félszögek összege 90o, tehát ha az egyenesek felezik az átlók szögeit, akkor merőlegesek egymásra.
|
| Előzmény: [1570] Vonka Vilmos Úr, 2012-05-27 20:25:16 |
|
| [1570] Vonka Vilmos Úr | 2012-05-27 20:25:16 |
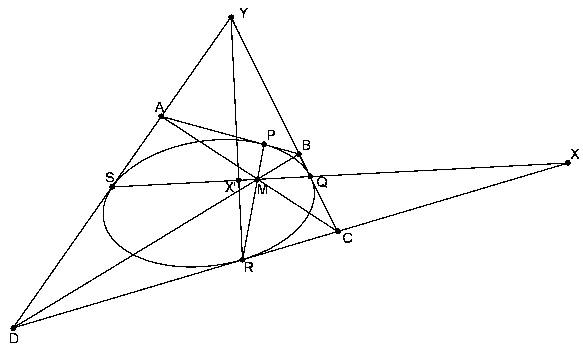
 A 181. feladat állításának belátásához elegendő azt ellenőrizni, hogy a szóban forgó négy egyenes harmonikus sugárnégyest alkot. Mivel ugyanis tetszőleges szöget tekintve a belső és külső szögfelezők harmonikusan választják el a szögszárakat (és a belső és a külső szögfelező pedig merőleges egymásra), az állítás mindkét oldala innen a harmonikus elválasztás tulajdonságait alkalmazva egyszerűen végiggondolható.
Azt, hogy a négy egyenes harmonikus sugárnégyest alkot, projektív geometriai módszerrel kicsit általánosabban, tetszőleges kúpszelet köré írt négyszögre fogom belátni. Az ábra jelöléseit használva, azt kell ellenőrizni, hogy (MC,MD,MR,MX) harmonikus sugárnégyes. Ez pontosan akkor teljesül, ha (CDRX) harmonikus pontnégyes, ami pedig a Pappos-Steiner tétel miatt ekvivalens azzal, hogy (QSX'X) harmonikus pontnégyes. Ez pontosan akkor teljesül, ha X és X' konjugáltak a négyszögbe írt kúpszeletre nézve. Mivel azonban látható, hogy Y polárisa QS, Y és X konjugáltak. Így X polárisa az RY=RX' egyenes, amiből következik, hogy X és X' valóban konjugáltak.
Természetesen érdekes lehet az eredeti állításra egy elemi geometriai bizonyítás is.
|
 |
| Előzmény: [1569] m2mm, 2012-05-27 18:19:14 |
|
| [1569] m2mm | 2012-05-27 18:19:14 |
 181. feladat: Bizonyítsuk be, hogy egy érintőnégyszög beírt körének szemközti érintési pontjait összekötő e1,e2 egyenesek pontosan akkor felezik az átlók által bezárt szöget, ha e1 és e2 merőlegesek egymásra.
|
| Előzmény: [1561] HoA, 2012-05-25 14:43:58 |
|
|
|
|
| [1565] m2mm | 2012-05-25 21:11:30 |
 "Egy érintőnégyszög beírt körének szemközti érintési pontjait összekötő egyenes áthalad az átlók metszéspontján."
Ez igaz. Legyen ABCD érintőnégyszög, AB és CD egyenesek metszéspontja a projektív síkon E, AD és BC-é F.
Gondold meg, hogy létezik vetítések egy szorzata(síkokra vetítünk), hogy a beírt kör körbe menjen, EF egyenes pedig ideálisba. Illeszkedéstartóság miatt az érintőnégyszög oldalegyeneseinek a képei érintik a kapott kört: ABCD A'B'C'D' képe érintőnégyszög. Mivel EF ideálisba ment, így A'B'||C'D' és A'D'||B'C', tehát A'B'C'D' paralelogramma és érintőnégyszög: rombusz. A rombusz szimmetriaközéppontján pedig nyilván átmegy az összes kérdéses egyenes. Az illeszkedés tartása miatt így az eredeti érintőnégyszögben is egy ponton mentek át a kérdéses egyenesek.
|
| Előzmény: [1561] HoA, 2012-05-25 14:43:58 |
|
|
|
|
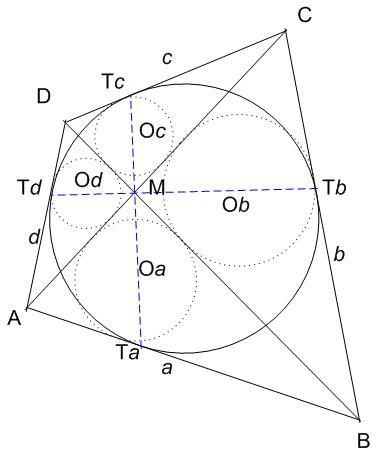
| [1561] HoA | 2012-05-25 14:43:58 |
 [1553] ábráját nézve bennem az merült fel: igaz-e, hogy pl. M, Oc és az érintőnégyszög beírt körének [1553] ábráján csak fekete pöttyel jelölt érintési pontja c-n (Tc) egy egyenesen van? Lehet, hogy ez közismert, de Vonka Vilmos úr hivatkozásaiban - és az onnan elérhető hivatkozásokban - nem láttam megemlítve. Vagy kicsit másképp fogalmazva, igaz-e a sejtés:
Egy érintőnégyszög beírt körének szemközti érintési pontjait összekötő egyenes áthalad az átlók metszéspontján és felezi az átlók által bezárt szöget.
|
 |
| Előzmény: [1553] BohnerGéza, 2012-05-22 09:26:24 |
|
| [1560] m2mm | 2012-05-23 15:23:10 |
 A feladat egy megoldása már fenn van a fórumon, a Lejárt határidejű KöMaL feladatokról [693] hozzászólásában. Ha jól látom a szintetikustól nem sokkal tér el (ő Desarguesozik én meg harmonikus pontnégyeseket használok az egyik lépésben).
|
| Előzmény: [1558] Vonka Vilmos Úr, 2012-05-23 07:00:15 |
|
| [1559] HoA | 2012-05-23 09:19:03 |
 A 179. feladat megoldása: Válasszuk úgy a betűzést, hogy Oc és Ob különböző távolságra legyen az AC átlótól, mint az ábrán is. ( Ha nincs ilyen lehetőség, akkor a négy kis háromszögbe írt kör sugara egyenlő és könnyen belátható, hogy érintőnégyszögünk rombusz, amelyre már szimmetria okokból is könnyen adódik A. 549 állítása ).
Érintőnégyszögünket az AC átlóra tükrözve és a betűzést az eredeti körüljárás szerint elvégezve az ObOcOd körre vonatkozó állítás most tkp. az eredeti ábra ObOcOa körére vonatkozik, tehát ha az első igaz, akkor a második is és viszont.
Az ObOcOd kör Ob és Oc –beli érintőinek metszéspontja legyen C1. Mivel ez rajta van MC-n és egyenlő távolságra van Ob-től és Oc-től, így MC és ObOc f felező merőlegesének metszéspontja. Ebből ObOcOd kör O1 középpontja is egyértelmű: mivel Ob és Oc rajta van az O1C1 átmérő Thálesz-körén, O1 az ObOcC1 kör és f másik metszéspontja.
A fentiekben Od-t nem használtuk fel, így ugyanerre az eredményre jutunk, ha az ObOcOa körből indulunk ki. A két kör középpontja tehát azonos és van a körvonalaknak közös pontja, pl. Ob, tehát a két kör egybeeseik, OaObOcOd egy körön vannak.
|
| Előzmény: [1553] BohnerGéza, 2012-05-22 09:26:24 |
|
| [1558] Vonka Vilmos Úr | 2012-05-23 07:00:15 |
 Egyébként az eredeti A. 549-es feladat "előéletével" és általánosításaival kapcsolatban itt van egy érdekes cikk, elsősorban a 4. fejezetet és a kapcsolódó hivatkozásokat érdemes megnézni. Ebben a folyóiratban a 243. oldalon az állítás a megfordításával együtt be van látva, de itt szintetikus bizonyítás is olvasható.
|
| Előzmény: [1557] BohnerGéza, 2012-05-23 03:50:33 |
|
|
|
|
| [1554] Lóczi Lajos | 2012-05-22 12:45:05 |
 180. feladat. Valamely p és q valós számok esetén tekintsük az f(x):=x2+px+q polinomot.
A (p,q) pont a síkon fussa be az origó középpontú egységsugarú körvonal peremét. Ekkor az f(x)=0 egyenlet gyökei a (komplex) síkon szintén körbejárnak.
Milyen alakzat áll elő így a gyökök mozgása során? Mutassuk meg, hogy
-- a (komplex) síkon az alakzatot magába foglaló, origó középpontú és minimális sugarú kör sugara 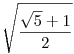 , ,
-- az alakzat területe pl. 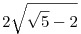 és és 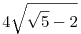 közé esik. közé esik.
|
|
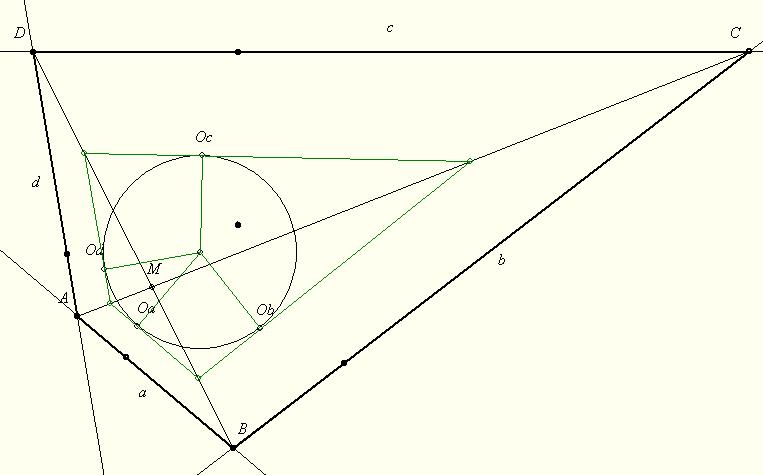
| [1553] BohnerGéza | 2012-05-22 09:26:24 |
 Az alábbi feladat megoldása nem jelent meg a KÖMAL-ban.
A. 549. Az ABCD érintőnégyszög átlói az M pontban metszik egymást. Mutassuk meg, hogy az ABM, BCM, CDM és DAM háromszögekbe írt körök középpontjai egy körön vannak.
A feladattal kapcsolatban a következő merült föl:
Legyenek a megfelelő középpontok Oa, Ob, Oc és Od. Az új állítás: Az ObOcOd körhöz az Ob-ben és Oc-ben húzott érintők az MC egyenesen metszik egymást. (Ennek bizonyítása valószínűleg az eredeti A. 549. feladattal egyforma nehézségű, vagy nehezebb.)
Viszont annak bizonyítása, hogy ebből az új állításból következik az eredeti, már emberi léptékű.
179. feladat: Bizonyítandó, hogy az új állításból következik az A. 549. feladat állítása.
|
 |
|
| [1552] BohnerGéza | 2012-05-09 11:13:00 |
 Maradok a nálam szokásos jelöléseknél, így kevesebb elírás várható.
Az oldalakon az érintési pontokat a szemközti csúcs nagybetűjével és indexekkel jelölöm: a beírt körhöz a 0, az érintőkörökhöz belül érintett oldal (a, b, c) az index.
Külső pontból a körhöz húzott két érintőszakasz hossza megegyezik:
ABo = ACo = x, BCo = BAo = y, CAo = CBo = z.
2(x+y+z)= k (kerület) x+y+z = s (félkerület), ahonnan pl.
x = s-(y+z) = s-a
Magyarul: Csúcstól a beírt körig tartó érintőszakaszt kapjuk, ha a félkerületből levonjuk a szemközti oldalt.
Mivel BCa = BAa, CAa = CBa és ABa = ACa, 2s = AaC+CA+AB+BCa = BaA+ACa.
Tehát ABa = ACa = s. Magyarul: Csúcstól a szemközti hozzáírt körig tartó érintőszakasz hossza a félkerület.
Ezeket tudva beláthatod, hogy kérdésedre a válasz PQ = |b-c|.
Érdekes eredményeket kapsz, ha meghatározod például a következő szakaszok hosszát:
CoCa, CbCa, BCa, BCo, ... (egy oldalegyenesen van két csúcs és 4 érintési pont, bármely kettő távolsága meghatározható.)
Ezek ismerete szerkesztési feladatokban is segíthetnek.
|
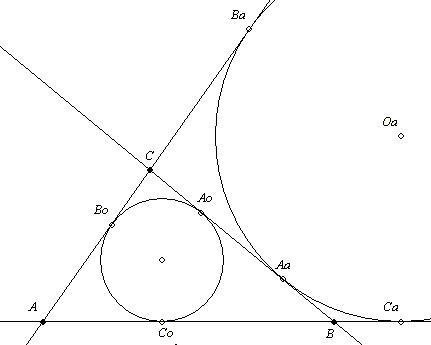 |
| Előzmény: [1550] matekpelducik, 2012-05-08 22:26:30 |
|
|
| [1550] matekpelducik | 2012-05-08 22:26:30 |
 Egy háromszög oldalainak hossza a, b és c.Érintse az a hosszúságú oldalt a beírt kör a P,a hozzáírt kör a Q pontban.Fejezzük ki a PQ szakasz hosszát b és c segítségével!
Ehez a feladathoz várnék megoldást :) Előre is köszi (Levezetve)
|
|
