| [636] BohnerGéza | 2007-02-12 22:00:07 |
 Egy aktuális, de egyáltalán nem közismert feladat:
B. 3970. Bizonyítsuk be, hogy egy egységnyi oldalú szabályos hétszög átlói hosszának harmonikus közepe 2.
|
| Előzmény: [632] Doom, 2007-02-11 11:15:38 |
|
| [635] Doom | 2007-02-11 13:35:31 |
 Ilyenekre gondoltam, köszi mindkettőtöknek!
|
|
|
| [633] V Laci | 2007-02-11 12:06:34 |
 Én most hirtelen két geometriai példát tudnék mondani:
1) Trapézban, a átlók metszéspontján át húzott, az alapokkal párhuzamos egyenes trapézon belüli része a két alap harmonikus közepe.
2) Háromszög egyik szögfelezőjére, a szemközti oldallal való metszéspontjából állított merőleges kimetsz egy szakaszt az egyik oldalból. Ez a szakasz a szögfelezővel szomszédos két oldal harmonikus közepe.
Ilyen "geometriai jelentésre" gondoltál?
|
| Előzmény: [632] Doom, 2007-02-11 11:15:38 |
|
| [632] Doom | 2007-02-11 11:15:38 |
 Nem tudjátok véletlenül, hogy a harmonikus középnek milyen geometriai jelentése van? Előre is kösz!
|
|
|
|
|
| [628] BohnerGéza | 2007-02-06 20:48:35 |
 Nem tudom, hogy képességvizsga feladatnak a 8. osztályosok számára jó-e a feladat. Talán nem. (HoA hozzászólása is ezt erősíti bennem) A lényege általánosabban is használható.
Nem kell, hogy a BAD szög derékszög legyen. Jelöljük ezt a szöget fí-vel, ekkor 180 fok - fí forgatással oldhatjuk meg a feladatot. Ennek speciális esete, ha fí 0 fok ( az e egyenes egy partján van A és B, jussunk el A-ból e-t érintve B-be a legrövidebb úton ).
Gondolkodhatunk így is: Használjunk egy AA'-t tartalmazó síktükröt! Állítsuk úgy, hogy B'-ből lássuk benne D-t! ...
Nehezítek kicsit a feladaton: 104. feladat: Jussunk el minnél rövidebb úton B'-ből AA'-t és DD'-t érintve C-be úgy, hogy AA' és DD' között adott irányt kell követnünk! ( Az irányt az AA'D'D síkkal párhuzamos egyenessel adhatjuk meg. )
|
| Előzmény: [626] Cckek, 2007-02-05 16:29:55 |
|
| [627] HoA | 2007-02-06 12:44:26 |
 Igen, a lényeg az, beugrik-e valakinek a síkba forgatás ötlete. Aki találkozott már a "pók legrövidebb útja a szoba falain a légyig" feladattípussal, annak persze nem nehéz.
|
| Előzmény: [626] Cckek, 2007-02-05 16:29:55 |
|
| [626] Cckek | 2007-02-05 16:29:55 |
 Szép megoldás. Amúgy ez a feladat képességvizsga feladat a 8. osztályosok számára, itt Romániában, és ha nem ismertem volna hasonló módszert nem tudom hogyan lehetett volna 8. osztályos szinten megoldani.
|
| Előzmény: [625] BohnerGéza, 2007-02-05 12:34:31 |
|
|
| [624] Cckek | 2007-02-05 05:20:14 |
 103.feladat Lehet hogy a forumozók elsiklottak a feladat fölött.:) Egy ABCDA'B'C'D' téglatest éleinek a hossza AB=a, BC=b, AA'=c. Legyen Q (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen
|
|
| [623] Cckek | 2007-02-05 05:19:01 |
 102. Lehet hogy a forumozók elsiklottak a feladat fölött.:) Egy ABCDA'B'C'D' téglatest éleinek a hossza AB=a, BC=b, AA'=c. Legyen Q (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen (AA'). Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen
|
|
| [622] Csimby | 2007-02-02 10:37:26 |
 Köszönöm a sok szép megoldást :-)
|
|
|
|
|
| [618] Cckek | 2007-01-31 22:22:35 |
 Jelölje ia,ib,ic a háromszog szögfelezőit a,b,c az oldalait, írhatjuk:
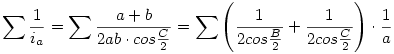 . .
Tehát csak annyit kell bizonyítani, hogy
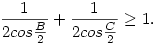 , ,
ami egyenértékű az
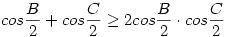 , ,
egyenlőtlenséggel. De a
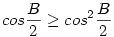
egyenlőtlenség miatt ez utóbbi fennáll.
|
| Előzmény: [617] Csimby, 2007-01-31 21:52:50 |
|
| [617] Csimby | 2007-01-31 21:52:50 |
 102.feladat Igaz-e és ha igen bizonyítsuk be, hogy tetszőleges háromszög szögfelezőinek a reciprokának az összege nagyobb az oldalai reciprokának az összegénél.
|
|
| [616] Cckek | 2007-01-31 21:43:36 |
 Nagyon érdekes feladat, főleg mivel általános iskolai színtű bizonyítást igényel. Egy ABCDA'B'C'D' téglatest éleinek a hossza a,b,c. Legyen Q AA'. Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen. AA'. Határozzuk meg a QA értéket, úgy hogy a B'QD háromszög kerülete minimális legyen.
|
|
|
| [614] HoA | 2007-01-30 10:46:31 |
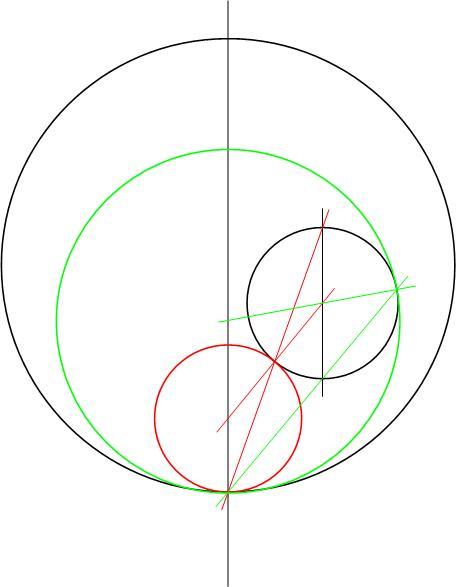
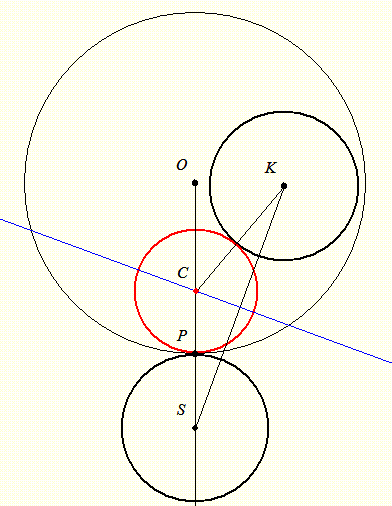
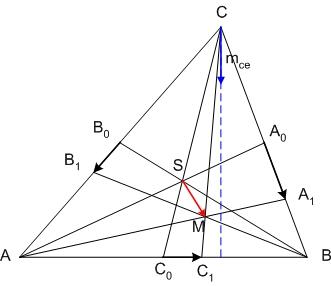
 A feladat a "Geometriai feladatok gyűjteményében" is szerepel. Az ottani megoldás sem bonyolult. Azon alapul, hogy a kis K2 kör és a szerkesztendő K3 kör T érintési pontja K2 és K3 hasonlósági pontja, és mivel C az OP egyenesen van, a hasonlóságban P megfelelője K2-n az OP-vel párhuzamos átmérő valamelyik végpontja (Q1, Q2). PQi kimetszi K2-ből T-t, TK és PO metszéspontja C. A választástól függően a K2-t kívülről illetve belülről érintő K3 kört kapjuk.
|
 |
| Előzmény: [613] lorantfy, 2007-01-30 09:13:35 |
|
| [613] lorantfy | 2007-01-30 09:13:35 |
 Szia Attila!
Kösz a megolgást! Végülis ilyen egyszerű az egész. Szemléletesebb talán azt mondani, hogy az S pontban vegyünk fel egy r sugarú kört. Így két egyenlő sugarú körhöz kell érintőkört szerkesztenünk, tehát a keresett C pont rajta van a szimmetria tengelyen, vagyis KS felező merőlegesén.
|
 |
| Előzmény: [612] jenei.attila, 2007-01-29 14:01:30 |
|
|
| [611] lorantfy | 2007-01-27 11:14:46 |
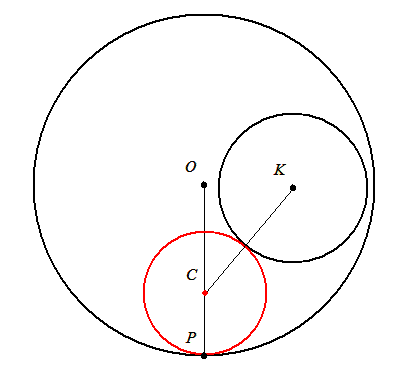
 102. feladat: Adott az O középpontú R sugarú kör és belsejében az O-tól különböző, K középpontú r sugarú kör. Szerkesszönk olyan kört, mely a nagy kört egy adott P pontban érinti és érinti a kisebb kört is!
|
 |
|
| [610] BohnerGéza | 2007-01-25 12:11:02 |
 101. feladat: ( Megpróbálom, hátha sikerül sorszámozni a további feladatokat. )
|
 |
|
|
| [608] epsilon | 2007-01-11 11:49:45 |
 Köszi, megnéztem, hát onnan látszik a feladat "fajsúlya" ;-)
|
|
|
| [606] epsilon | 2007-01-11 11:14:12 |
 Hmmmm....hát kellett nekem :-) valóban implicit, mégis valamivel barátságosabbra gondolta, ez is a körszeletekből származik? Mert Én úgy próbáltam, hogy 2 szembennálló körszelet összegeként fogtam fel, a 2 körben, ott egzenlőre a sugár ami ismeretlen, meg 2 középponti szög, persze lehet kifejezni...de gyökös összefüggések lettek :-( Ha jó hallottam, ezt a feladatot valamikor a Danubiusz rádióban adták fel, és azt szeretném megtudni, hogy vajon milyen megoldást vártak volna el, pontosabban milyen eredményt, a helyes megoldásként...vagy csak szívatás volt?
|
|
|
|
| [603] epsilon | 2007-01-11 10:15:43 |
 Helló Cckek! Az igazolása affixumokkal csak algebrai számolás. Az illető csúcs megfelelő kisbetűjével jelölve az illető affixumot, a bizonyítandó összefüggés: 4(o1-h)+ 4(o2-h)+ 4(o3-h)= 15(g-h) vagyis 4(o1+o2+o3)=15g-3h és legyen a köréírt kör középpontja éppen az O origó, ekkor g=(a+b+c)/3 és h=a+b+c, és így elegendő bizonyítani, hogy: 2(o1+o2+o3)=a+b+c (*). Az előző indoklás alapján PO vektor=2 RO1 vektor (a az indoklást lásd előbb) és ezt affixumokkal felírva 0-p=2(o1-r)továbbá p=(b+c)/2, r=(m+n)/2 és az m, n a felezőpontokra vonatkozó affixumokat is használva, o1=a/2 adódik és analógjai (ezt még másképpen is bizonyíthatjuk) és a (*) összefüggés így valóban teljesül. (a bizonyítandó kép a hszm alján van!)
|
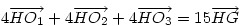 |
| Előzmény: [593] HoA, 2007-01-08 15:59:17 |
|
|
| [601] epsilon | 2007-01-10 22:07:38 |
 Kösz a megjegyzést, valóban ott van, most olvastam az ott leírt megjegyzéseket, ...de nem bíztatóak, valamilyen kifejezést szeretnék találni az R függvényében (nem megközelítő megoldást)de a körszeletekkel elindulva, két körszeletből összerakva egyenlőre semmi bíztató nem jött ki (még maradt kiküszöböletlen paraméter is :-(
|
|
| [600] psbalint | 2007-01-10 21:44:42 |
 azt hiszem éppen erről a feladatról volt szó az Érdekes matekfeladatok topikban
|
|
| [599] epsilon | 2007-01-10 20:48:52 |
 Helló! BÚÉK Mindenkinek! Létezik-e elemi megoldás a következő, ismertnek tűnő feladatra: Adott egy 1 egységsugarú körlap. Annak kerületén vegyünk fel egy tetszőleges M pontot, és az M középponttal, R sugárral rajzoljunk egy körívet, ami az adott körlapot két kükönböző pontban metszi. Mekkora kell legyen az R, hogy a "közrezárt" síkrész területe az 1 sugarú kör területének a fele legyen? Előre is kösz az esetleges támpontokat! Üdv: epsilon
|
|
| [598] HoA | 2007-01-10 15:51:57 |
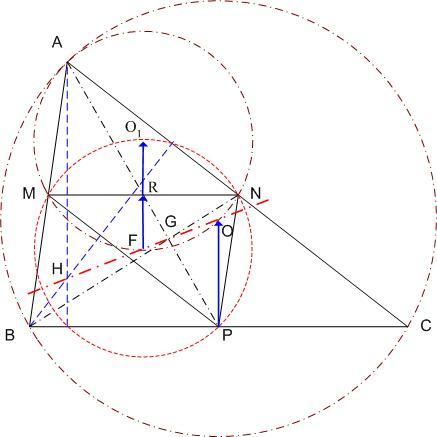
 A bizonyítás, ahol egy 3-as szorzóval elszámoltam magamat :-) : Cckek jelöléseivel ( ha már... ), legyen a körülírt kör középpontja O, a Feuerbach köré F, MN felezőpontja R. ABC  az AMN az AMN  A-ból vett kétszeres nagyítása, így A-ból vett kétszeres nagyítása, így 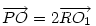 . AMN . AMN  és PNM és PNM  egymás tükörképei R-re, ezért egymás tükörképei R-re, ezért 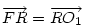 , vagyis , vagyis 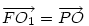 . .
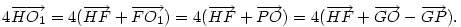 Hasonlóan Hasonlóan 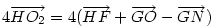 és és 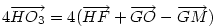 A hármat összeadva A hármat összeadva 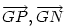 és és 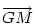 kiesik, mert egy kiesik, mert egy  súlyvonalainak harmadai, így vektorösszegük súlyvonalainak harmadai, így vektorösszegük  . Igazolandó : . Igazolandó : 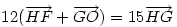 . Legyen az Euler-egyenesen . Legyen az Euler-egyenesen 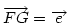 . Ekkor . Ekkor 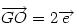 , ,  és és 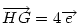 . Egyenlőségünk tehát . Egyenlőségünk tehát 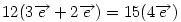 , amit már nem nehéz belátni. , amit már nem nehéz belátni.
|
 |
| Előzmény: [595] HoA, 2007-01-09 11:13:46 |
|
|
|
|
| [594] Cckek | 2007-01-08 21:12:11 |
 Legyen G az ABC háromszög súlypontja, H az ortocentruma, M, N, P az AB, AC, BC oldalak felezőpontjai, O1,O2,O3 az AMN, BMP illetve CNP háromszögek köré írt körök középpontjai. Bizonyítsuk be hogy : 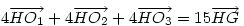
|
|
| [593] HoA | 2007-01-08 15:59:17 |
 Mivel két hete senki sem szólt hozzá, leírok egy megoldást. Nézzük meg, mi a mértani helye a síkban azoknak a pontoknak, melyekre az ABC  csúcsaitól mért távolságok négyzetösszege csúcsaitól mért távolságok négyzetösszege
adott konstans?
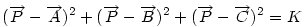
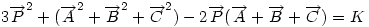 Ha origónak az ABC Ha origónak az ABC  S súlypontját választjuk, S súlypontját választjuk, 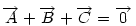 ; ;  , ami adataink által meghatározott konstans. A mértani hely tehát egy S középpontú kör, a sugár négyzete a jobboldali kifejezés, ami akkor nemnegatív, ha , ami adataink által meghatározott konstans. A mértani hely tehát egy S középpontú kör, a sugár négyzete a jobboldali kifejezés, ami akkor nemnegatív, ha 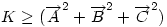 (1) baloldala tehát akkor a legkisebb, ha P a súlypont, értéke ekkor (1) baloldala tehát akkor a legkisebb, ha P a súlypont, értéke ekkor 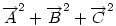 . Most már csak azt kell igazolni, hogy ez megegyezik a háromszög oldalai négyzetösszegének harmadával. De . Most már csak azt kell igazolni, hogy ez megegyezik a háromszög oldalai négyzetösszegének harmadával. De 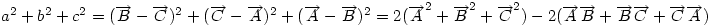 Origó választásunk miatt Origó választásunk miatt 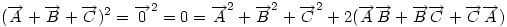 Innen Innen 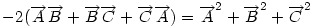 Tehát valóban Tehát valóban 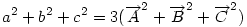
|
| Előzmény: [588] BohnerGéza, 2006-12-25 22:50:17 |
|
| [592] Sirpi | 2007-01-05 16:10:42 |
 Ezt hívják Euler-egyenesnek, és ráadásul az S pont harmadolja (O-hoz közelebb) az OM szakaszt.
Egybe akkor és csak akkor esnek, ha a háromszög szabályos.
|
| Előzmény: [591] Cckek, 2007-01-05 16:04:29 |
|
| [591] Cckek | 2007-01-05 16:04:29 |
 Igaz-e, hogy bármely háromszögben az ortocentrum, a súlypont és a háromszög köré írt kör középpontja kollineárisak? (vagy egybeesnek:)
|
|
|
| [589] HoA | 2006-12-27 10:11:54 |
 BohnerGéza ábrája alapján ha az  , , , , paraméterekkel kifejezett koordinátákra felírjuk az paraméterekkel kifejezett koordinátákra felírjuk az 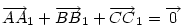 vektoregyenletet, rövid számolás után kapjuk, hogy vektoregyenletet, rövid számolás után kapjuk, hogy  = = = = , vagyis P (Cckek-nél M) = , vagyis P (Cckek-nél M) = 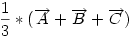 , vagyis M a súlypont. , vagyis M a súlypont.
Ha [582] "akkor" ágának bizonyítására elfogadjuk az [586] ábráját, a "csak akkor" ágra itt egy - talán kicsit szemléletesebb - bizonyítás. Legyenek a háromszög oldalfelező pontjai A0,B0,C0 , a súlypont S, továbbá M, A1,B1,C1 [582] szerint. A súlyvonalak a háromszöget hat kis háromszögre osztják. Az általánosság megszorítása nélkül feltehetjük, hogy M a C0BS háromszög belsejében vagy határán van. Mivel pl. 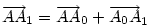 és tudjuk, hogy és tudjuk, hogy 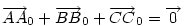 , , 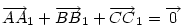 pontosan akkor teljesül, ha pontosan akkor teljesül, ha
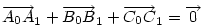 | (1) |
. Ha a három vektor összege 0, akkor tetszőleges irányú vetületüké is az. Tekintsük az mc magasságra vett vetületeket - az mce egységvektorral vett skaláris szorzatokat. Ez 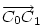 esetében nyilván 0. M választása miatt A1 nincs messzebb B-től, mint A0 és B1 nincs messzebb A-tól, mint B0 . Így esetében nyilván 0. M választása miatt A1 nincs messzebb B-től, mint A0 és B1 nincs messzebb A-tól, mint B0 . Így 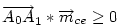 és és 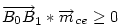 . Ezért (1) csak úgy teljesülhet, ha A0=A1 és B0=B1 , vagyis M=S. . Ezért (1) csak úgy teljesülhet, ha A0=A1 és B0=B1 , vagyis M=S.
|
 |
| Előzmény: [587] BohnerGéza, 2006-12-25 22:49:35 |
|
|
|
|
| [585] HoA | 2006-12-23 09:19:45 |
 Azt hiszem az ellentmondás feloldása az, hogy Ti szakaszokról beszéltek, a feladat pedig vektorokról szól: az AA1, BB1, CC1 vektorok pontosan akkor alkotnak vektorháromszöget , ha M a súlypont. Lehet, hogy Cckek ezt akarta a szögletes zárójelekkel jelezni.
|
| Előzmény: [584] Cckek, 2006-12-22 21:02:28 |
|
|
| [583] jenei.attila | 2006-12-22 20:21:22 |
 Ezt sajnos nem értem. Azt akarod mondani, hogy ha a súlyponttól csak egy "kicsit különböző" pontot veszünk, akkor a szóbanforgó szakaszokból nem szerkeszthető háromszög? Ezek a szakaszok az M pont megválasztásával nyilván folytonosan változnak, tehát a súlyponttól való kis eltérés a hosszukban is kis változást eredményez. A háromszög egyenlőtlenségbe pedig még biztos hogy belefér egy kis változás. Valamit nyilván félreértek, pontosítanád egy kicsit?
|
| Előzmény: [582] Cckek, 2006-12-22 16:56:49 |
|
| [582] Cckek | 2006-12-22 16:56:49 |
 Legyen M az ABC háromszög egy belső pontja. AM,BM,CM a szemközti oldalakat metsze rendre az A1,B1,C1 pontokban. Bizonyítsuk be, hogy [AA1],[BB1],[CC1] szakaszok akkor és csak akkor egy háromszög oldalai ha M az ABC háromszög súlypontja.
|
|
| [581] Hajba Károly | 2006-11-23 15:30:14 |
 Én sem.
Az [577]-es válaszom után még motoszkált valami a fejemben és elkezdtem firkálgatni (a pitagórászi ábrácskára a köröket, az ábra jobb felső sarkában) és belémcsapot az isteni szikra. :o)
|
| Előzmény: [580] AzO, 2006-11-23 15:06:26 |
|
|
|
| [578] Hajba Károly | 2006-11-22 08:47:12 |
 Csimby!
Nem számoltál még be, hogy mire jutottatok?
---
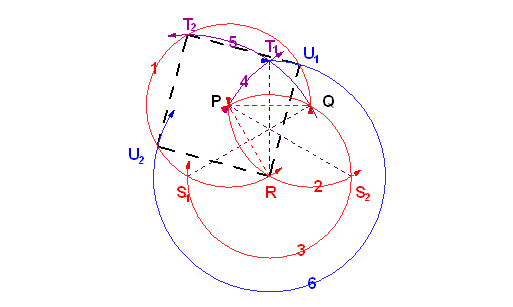
Én közben találtam egy "igaz" 6 körös megoldást, ebben nincs mérés miatti körzőmozgatás:
|
 |
|
| [577] Hajba Károly | 2006-11-22 00:07:35 |
 Én fenn a Gellért-hegyen egy csillagász szakkörön hallottam és főleg a középiskolásoknak adták föl, én ott csak vízhordó voltam. :o)
Szóval a szakkörvezető így kezdte: Már az ókori görögök is ...
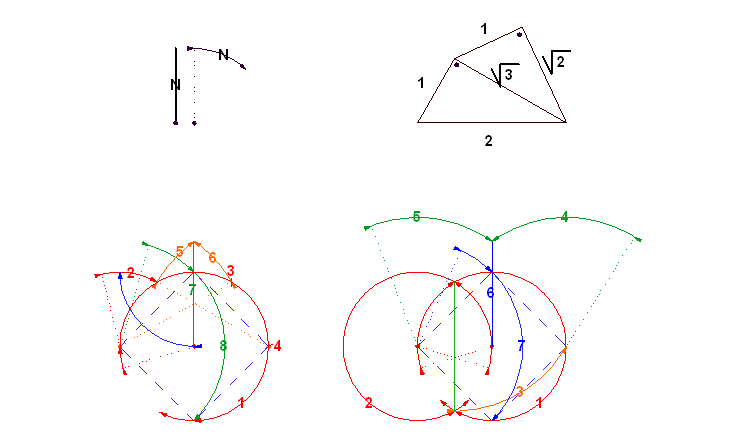
A definició, najó legyen csak "definició" szerint ScarMan megoldása valóban 7 körző-felemeléses, mert a 3. lépés távolságát használja fel a 4. és 5. lépésben. Lásd az ábrámat, melyen az én megoldásomat és az övét is felszerkesztettem.
Értelmező ábrácska a bal felső fekete, vastag vonal: mérés, nyilazott ív: körzőzés.
ScarMan-nak meg még egy grat.
|
 |
| Előzmény: [576] AzO, 2006-11-21 23:10:25 |
|
| [576] AzO | 2006-11-21 23:10:25 |
 Az 1977-es feladatot nem Napoleon-feladat-nak hivjak? Mintha olvastam volna valahol mostanaban. A definiciomert nem vallalok felelosseget, mert csak emlekezetbol mondtam, es akkor az en 7 lepeses megoldasom is mar 8 :)))
|
| Előzmény: [575] Hajba Károly, 2006-11-21 08:33:01 |
|
| [575] Hajba Károly | 2006-11-21 08:33:01 |
 Üdv a körösöknek! és grat ScarMan-ek is!
Nem kekeckedni szeretnék, de AzO definiciója szerint - körző felvétele a lépés vége - csak 8 lépésből lehet megszerkeszteni. Az alább közöltem megoldás 7 körzőzés és 1 mérés, ScarMan-nek 6 körzőzés és 2 mérés. S gyanítom, hogy a feladatban nem véletlen volt 8 lépés kitűzve, főleg ELTE matekon.
Mellesleg alább -habár gyanítom nem eléggé értelmezhető módon- az én megoldásom is ott van. Volt ez pár éve kérdés az "Éredekes matekfeladatok"-ban, akkor megoldottuk, ha jól emlékszem, Jenei Attila adta a másik megoldást. (4.1, ill. 4.2)
Az akkori megoldásomban a két adott pont a négyzet két sarokpontja, ehhez +1 körzőzés kell, de így szerintem más sem tudja rövidebben, míg az eddig megismert egyéb megoldásnál az egyik pont nem a négyzet sarokpontja, hanem a közepe. Ezt szerkesztette meg korábban J. A.
Én anno 1977-ben így hallottam a feladatot: Osszunk négy egyenlő részre egy körívet csak körző használatával! (Akkor 8-ikos koromban a feladat győzött. :o) Ez -a fenti definíció szerint- 7 lépésből megoldható, mivel adott volt már egy körív.
|
| Előzmény: [574] AzO, 2006-11-20 22:59:09 |
|
| [574] AzO | 2006-11-20 22:59:09 |
 Szerintem is 6 lepes. Grat! :)
|
|
|
| [572] ScarMan | 2006-11-20 20:18:42 |
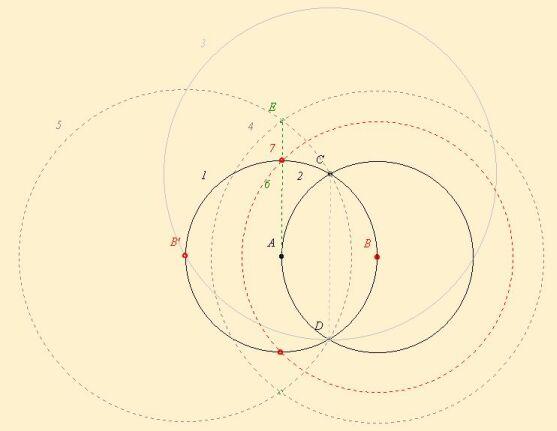
 Itt egy 7-lépéses megoldás: két adott pont: A, B, mindkét pontból AB sugarú köröket rajzolunk, ezek metszéspontja: C, D. C-ből D-n átmenő kört rajzolunk -> B'. B és B' középpontú, CD sugarú köröket rajzolunk. Egyik metszéspontjuk E. B-ből EA sugarú kört rajzolunk (itt külön lépésnek vettem, hogy körzőnyílásba vesszük EA-t), ez kimetsz két pontot az eredeti A középpontú körből. Ez a két pont B-vel és B'-vel négyzetet alkot.
|
 |
|
| [571] psbalint | 2006-11-20 17:45:50 |
 Tévedek akkor ha azt mondom hogy ezt a feladatot az egyik Gerőcs-féle Repeta matek kötetben is meg lehet találni?
|
|
| [570] Mumin | 2006-11-20 16:18:51 |
 Szabad a gazda. Az évfolyamból több embernek elég volt 7 körzőhasználat is, és ez a megoldás nem is túl bonyolult. A lényeg: a Pithagorasz-tétel.
|
| Előzmény: [560] AzO, 2006-11-14 22:54:59 |
|
| [569] The Student | 2006-11-18 12:26:13 |
 Ha megígéritek, hogy én is ilyen okos leszek, akkor lehet, hogy elmegyek matematikusnak! :) Na jó üdv mindenkinek! Én
|
|
| [568] Hajba Károly | 2006-11-17 20:17:57 |
 OK köszi, sejtem a dolgot. :o)
Ha bevetem a Pappos-tételét, akkor már egy tetszőleges P ponta tudok egy e egyenessel párhuzamost fektetni -egy körzővel-. De hogyan kell merőlegest? Ill. visszatérve a négyzetre: adott két pont, mely a négyzet két sarokpontja. Hogyan tudom a kétféle négyzetet megszerkeszteni?
|
| Előzmény: [566] jonas, 2006-11-17 17:56:10 |
|
|
| [566] jonas | 2006-11-17 17:56:10 |
 Rendben, mutatom hogy szerkesztek négyzetet egy körzővel. Valószínűleg ennél sokkal egyszerűbb módszer is van, de ez jutott eszembe elsőként.
Először is elmondom, hogy lehet csak vonalzóval két adott párhuzamos egyeneshez egy harmadik párhuzamos egyenest szerkeszteni adott ponton át. Ez a Desargues-tételen alapul. Legyen e és f a két párhuzamos egyenes, és G1 az adott pont. Vegyünk fel egy tetszőleges O pontot. Legyen az OG1 egyenes metszéspontja e-vel illetve f-fel E1 illetve F1. Egy másik, az O-n átmenő tetszőleges egyenes az e és f egyenest az E2 és F2 pontban metszi. Legyen E1F2 és E2F1 metszete P. A G1F2 és az OP metszete legyen Q. Ez után az F1Q és az OF2E2 egyenesek metszete legyen G2. Végül G1G2 lesz a keresett g párhuzamos egyenes. (Én matematikus vagyok, ezért ezt a szerkesztést csak elméletben tudom elvégezni, valódi vonalzóval nagyon pontatlan lesz, de mivel te mérnök vagy, talán el tudod helyezni úgy a pontokat, hogy ne legyen túl nagy eltérés.)
Ha már ezt tudjuk, akkor a négyzet sem okozhat nehézséget. Ugyanis legyen k egy K középpontú kör. Ha most AB a kör egy húrja, akkor összekötve őket K-val az átmérők másik végpontjai C és D, így kapunk egy ABCD téglalapot. Ezután a téglalap párhuzamos oldalegyenesihez szerkeszthetünk K-n át párhuzamost, így kapunk két merőleges átmérőt, amiknek a végpontjai egy négyzetet határoznak meg.
|
| Előzmény: [565] Hajba Károly, 2006-11-17 08:51:12 |
|
|
| [564] josie | 2006-11-16 13:31:42 |
 szabályos testekről és a gúláról kénne minden!!!
|
|
|
| [562] S.Ákos | 2006-11-15 18:47:30 |
 Egy kissé egyszerűbb kérdés: mennyi a minimális körzőhasználatok száma, ha vonalzót is használhatunk?
|
|
|
| [560] AzO | 2006-11-14 22:54:59 |
 Tenyleg ne aruld el hetfoig!!! Csak korzo hasznalata engedelyezett. Egy lepes addig tart, amig fel nem emeled a korzot. 2 pont adott a sikon, es kell 4 metszespont, ami negyzetet alkot. Legfeljebb 8 lepeses megoldas eseten +1 jegy a vizsgan.
|
| Előzmény: [556] Hajba Károly, 2006-11-14 20:55:26 |
|
|
|
|
| [556] Hajba Károly | 2006-11-14 20:55:26 |
 Nem mondok több infót, csak kérdezek. :o)
A feladat szerint egy üres papírra kell köríveket rajzolni úgy, hogy 4 darab metszéspont épp egy négyzetet adjon ki? és ehhez legfeljebb 8 körív rajzolható? A köríven egy tetszőleges pont bejelőlése az lépés?
Vagy adott két pont és erre kell négyzetet szerkeszteni?
|
| Előzmény: [552] Csimby, 2006-11-14 18:38:13 |
|
|
|
| [553] The Student | 2006-11-14 18:45:19 |
 Így lesz, remélem! Itt szerintem amúgy sem a feladatról van szó, hanem a 8 lépésről nem? Nekem csak az a lényeg, hogy a feladat menjen! És azt sem tudod még megszerkeszteni? Vagy csak a 8 lépéses dolog nem megy neked?
|
|
| [552] Csimby | 2006-11-14 18:38:13 |
 Pont azt kértem, hogy több infót itt NE közöljetek mert az egész évfolyam körzővel mászkál az egyetemen annyira lázba hozott mindenkit a téma és nem lenne jó ha itt lelőné valaki a poént amit egyenlőre még én sem tudok :-) Szóval Studenttel beszéljétek meg e-mailben...
|
| Előzmény: [549] Hajba Károly, 2006-11-14 08:30:05 |
|
| [551] The Student | 2006-11-14 16:43:44 |
 A megoldásodhoz fűznél egy kis magyarázatot, mert azért 10.es létemre nem annyira értem :)
|
|
| [550] The Student | 2006-11-14 16:24:19 |
 Köszi, aki segített, majd kibogarászom! És a Batthyány Kázmér gimibe :D csak nekünk ilyen jófej példákat kellene megoldani 10.-ben :D Hát nem vicces, de kapok érte ötöst... Üdv: Én
|
|
|
| [548] Csimby | 2006-11-14 01:43:26 |
 Ja és légyszi több infót ne közöljetek erről a példáról ugyanis ma adták fel az ELTE matematikus szakán és aki jövő hétig 8 lépésből megoldja +1 jegyet kap a geometria vizsgán.
|
| Előzmény: [547] Csimby, 2006-11-14 01:28:57 |
|
|
|
|
| [544] BohnerGéza | 2006-11-13 22:15:45 |
 Az [533]-ban lévő feladatra:
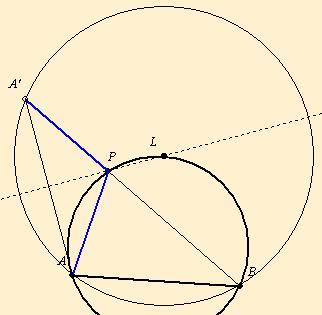
Az [537]-ben jenei.attila írt vázlatosan erről: A nem kisebbik ív nyilvánvaló. A két oldal összeadásához tükrözzük A-t az APB= gamma szög külső szögfelezőjére: A'. Ekkor BA' a keresett összeg. BA'A= gamma/2. A' az AB gamma/2 látókörén van, ennek középpontja L. BA' a leghosszabb, ha átmérője a látókörnek, azaz P=L.
|
 |
| Előzmény: [533] fermel, 2006-11-12 22:59:26 |
|
| [543] The Student | 2006-11-13 20:48:32 |
 Srácok fogy az idő (és lányok) valamit nem segítenétek, emrt én ehhez nem vagyok elég... Előre is köszi!
|
|
| [542] fermel | 2006-11-13 20:38:09 |
 Csimby és Attila! Nagyon köszönöm a segítségeteket.
Attila! Azt,hogy B' is rajta van azon a bizonyos körön, hogyan láttad be? Én szögekkel próbálkoztam, de még nem jött ki. Lehet, hogy túlbonyolítom? Segítenél? Köszönöm.
fermel
|
|
| [541] The Student | 2006-11-13 20:29:40 |
 Látom, ez is egy használható tanács volt! Köszi
|
|
|
|
| [538] The Student | 2006-11-13 18:49:08 |
 Sziasztok, új vagyok itt, de remélem sikerül érdekes témákat hoznom, illetve segítenem, bár eléggé tudtalan vagyok! Tudna nekem valaki segíteni, hogy hogy lehet megszerkeszteni csak körzővel egy négyzetet? Ha igen, akkor kérlek gyorsan írjatok, mert kell a házimba :) Köszi!
|
|
| [537] jenei.attila | 2006-11-13 11:12:11 |
 Ha jól emlékszek, ez nem rég kömal feladat volt. Vegyük a PA PB közül a hosszabbikat (pl. PA-t), ezt P felé meghosszabítva B'-t vegyük fel úgy, hogy PB'=PB legyen. Ekkor PA+PB=AB'. F legyen a z hosszabbik AB ív felezőpontja. Könnyű bizonyítani, hogy az F középpontú körön, amely átmegy A-n és B-n, rajta van B' is. Ezért a kérdéses összeg akkor maximális, ha AB' átmérője az F középpontú körnek.
|
| Előzmény: [533] fermel, 2006-11-12 22:59:26 |
|
