| [1447] Csimby | 2010-09-08 02:16:06 |
 Szóval mindenképpen ajánljuk, hogy megrendeld a lapot és csináld a pontversenyt - szerintem rengeteget lehet tanulni belőle - de itt a fórumon többnyire más feladatok kerülnek elő!
|
| Előzmény: [1446] BohnerGéza, 2010-09-08 00:59:23 |
|
| [1446] BohnerGéza | 2010-09-08 00:59:23 |
 Természetesen sok a lapban megjelenő feladat is előkerül itt, de a kettő nem fedi egymást.
A Lapban sok érdekes feladat van különböző nehézségűek csoportosításával. Az "A" jelűek nehezek, könnyebbek a "B"-k, kezdőknek a "C" jelűek valók, illetve kifejezetten kilencedikeseknek szólnak a "K" jelűek. Számítástechnikai és fizikai rovat is található sok érdekes feladattal.
A feladatok mellett nívós cikkek is vannak, sok kitűzött feladat megoldása is szerepel, valamint a pontverseny állása is félidőben, illetve a végeredménye.
|
| Előzmény: [1443] kuklic, 2010-09-06 18:16:49 |
|
| [1443] kuklic | 2010-09-06 18:16:49 |
 A feladatokat amiket itt megoldtok, a megrendelt komal lapból csináljátok? mert ha igen akkor megrendelem én is :)
|
|
| [1442] BohnerGéza | 2010-09-04 11:44:38 |
 Néhány megjegyzés a 171. feladathoz, és HoA szép megoldásához:
- Ha érintőkörökkel definiálunk valamit, érdemes lehet analóg feladatokat is megfogalmazni! ... (Valaki a 171. feladathoz?)
- A trapéz átlóinak metszéspontján átmenő, az alapokkal párhuzamos egyenesnek a trapézban lévő szakasza az alapok harmonikus közepe. (Ezt a szakaszt felezi az átlók metszéspontja, tehát a feladatban a magasság felezőpontja szerepel.) Ebből is folytatható a "volt egyszer..." helyett HoA megoldása.
Érdemes lehet tudni:
Ha a trapéz szárait az alapok arányában osztjuk, az osztópontokat összekötő szakasz az alapok mértani közepe. (Ha fordított arányban osztjuk, azt nem tudom, érdemes lehet kiszámolni!)
A trapéz szárainak felezőpontjait összekötő szakasz az alapok számtani közepe.
Ha a trapézt az alapokkal párhuzamosan úgy osztjuk ketté, hogy a területét felezzük, az osztóvonal az alapok négyzetes közepe lesz.
Ezekkel két számra igazolhatóak a szereplő közepekre az egyenlőtlenségek.
|
| Előzmény: [1441] HoA, 2010-08-19 13:19:44 |
|
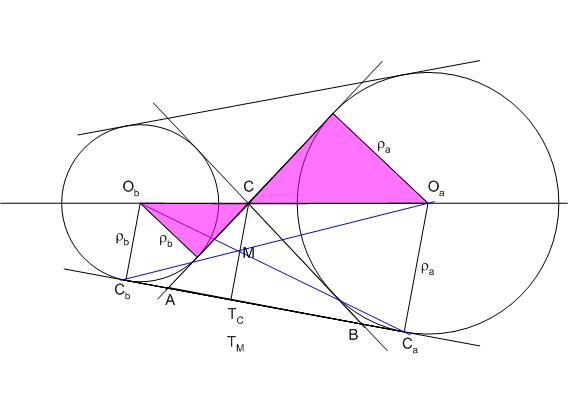
| [1441] HoA | 2010-08-19 13:19:44 |
 Egészítsük ki az ábrát a hozzáírt körökkel és közös érintőikkel. A lila háromszögek hasonlóságából és a párhuzamos szelők tételéből 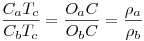 . Vagyis Tc a hozzáírt körök sugarainak arányában osztja a CaCb szakaszt. Az OaObCbCa derékszögű trapéz átlóinak M metszéspontjából CaCb -re bocsátott merőleges talppontja legyen TM Mivel CaTM és CbTM az OaCaM és ObCbM hasonló háromszögek megfelelő magasságai, ezek aránya is . Vagyis Tc a hozzáírt körök sugarainak arányában osztja a CaCb szakaszt. Az OaObCbCa derékszögű trapéz átlóinak M metszéspontjából CaCb -re bocsátott merőleges talppontja legyen TM Mivel CaTM és CbTM az OaCaM és ObCbM hasonló háromszögek megfelelő magasságai, ezek aránya is 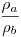 , TM és Tc egybeesik, M valóban rajta van CTc -n , TM és Tc egybeesik, M valóban rajta van CTc -n
Volt egyszer egy KöMaL feladat, amelyik azt kérdezte, megszerkeszthető-e a háromszög ha adott két hozzáírt kör sugara és a harmadik oldalhoz tartozó magasság. Eredményül persze kijött, hogy a három szakasz nem független, a magasság a két sugár harmonikus közepe, így vagy nincs megoldás vagy a feladat határozatlan. Ezt ismertnek feltételezve, a B 4276 annak bizonyítását kéri, hogy a harmonikus közép nem nagyobb a mértani középnél, ami e fórum látógatói számára érdektelen.
BohnerGéza ábrája viszont úgy is értelmezhető, hogyan szerkeszthetjük meg egyszerűen két szakasz harmonikus közepét. Hirtelenjében erre nem látok jobb megoldást.
|
 |
| Előzmény: [1440] BohnerGéza, 2010-08-04 02:02:39 |
|
| [1440] BohnerGéza | 2010-08-04 02:02:39 |
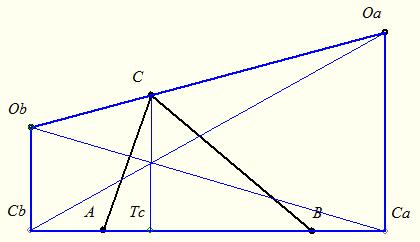
 171. feladat: A B.4276 feladattal kapcsolatban:
Az ABC háromszög két hozzáírt körének középpontja Oa és Ob, ezek érintési pontja az AB oldalon Ca és Cb A C-ből induló magasság CTc. Bizonyítandó, hogy OaCb és ObCa a CTc szakaszon metszik egymást.
|
 |
|
| [1439] gida1 | 2010-07-22 11:47:36 |
 Nagyon köszönöm, Jonas!
|
|
|
| [1437] gida1 | 2010-07-22 01:27:14 |
 Sziasztok! A segítségeteket kérném. Mi a magyar megfelelője az angol PERMUTOHEDRON-nak? Milyen éder? Segítségül egy link: http://en.wikipedia.org/wiki/Permutohedron
És mi az a BIPARITE GRAPH / BIGRAPH? http://en.wikipedia.org/wiki/Bipartite
Segítségeteket előre is köszönöm!
|
|
|
| [1435] S.Ákos | 2010-07-10 21:13:54 |
 170./a: k körre vonatkozó inverzióval, vázlatosan
AB képe az AOBFE kör, az O-n átmenő 3 kör (AEO, CDO, FBO képe 1-1 egyenes, rendre AE, CD, FB, AOB, AOC, COD, DOB egyenlőszárú háromszögek. Az állítás az, hogy EA és BF azonos szöget zár be CD-vel. Innét szögszámolással adódik, hogy tényleg egyenlő a két szög, (mondjuk legyen BAO =ABO =ABO = = és AOE és AOE = = 1, COD 1, COD = = 1, DOB 1, DOB = = 3). 3).
|
 |
| Előzmény: [1431] HoA, 2010-06-24 12:43:03 |
|
| [1434] sakkmath | 2010-07-10 20:46:09 |
 Túlbonyolítottam. Rájöttem, hogy nem kell az inverzió. Elég azt látni, hogy mivel a k3 körben N1 N2 húr, ezért őt merőlegesen felezi MO. Ezért az N1 N2 O háromszög egyenlő szárú, stb. (Elnézést.)
|
| Előzmény: [1433] sakkmath, 2010-07-10 18:59:21 |
|
|
|
| [1431] HoA | 2010-06-24 12:43:03 |
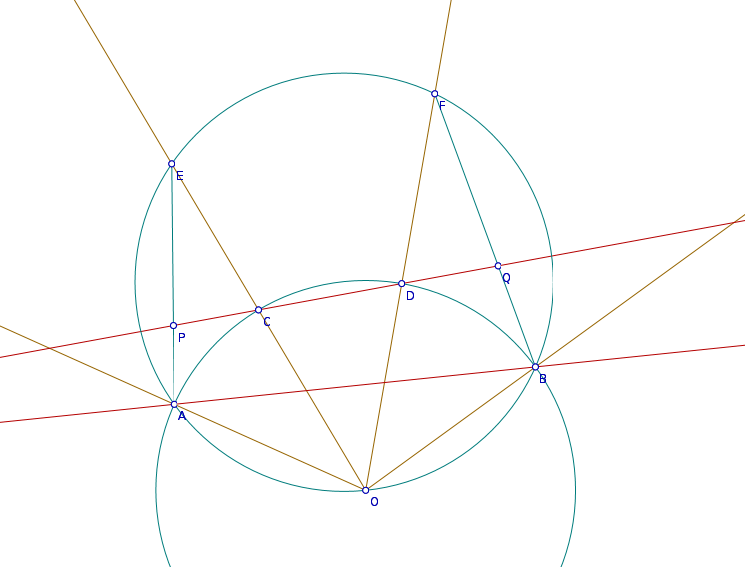
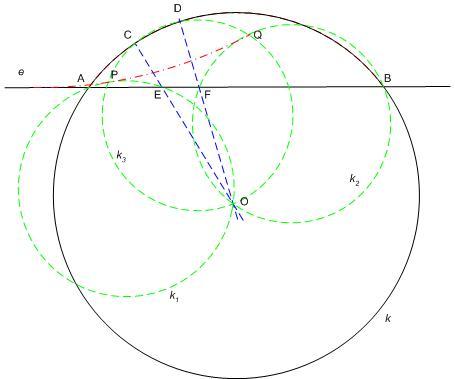
 170. feladat Az O középpontú k kört az e szelő az A és B pontokban metszi.Az AB ív C és D pontjába húzott sugár metszéspontja e-vel E és F.
a)Igazoljuk, hogy az AEO pontok k1 köre és a BFO pontok k2 köre azonos szögben metszi az OCD pontok k3 körét. Az O-tól különböző metszéspontok P és Q.
b)Bizonyítsuk be, hogy a k1-et P-ben és k2-t Q-ban érintő kör e-t is érinti.
|
 |
|
| [1430] HoA | 2010-06-16 12:25:39 |
 A 165. [1422] feladat megoldása. E fórum olvasóinak, feladatmegoldóinak sokkal tömörebben is elég lenne, de szerintem tanításban jól használható, így kicsit részletesebben írok.
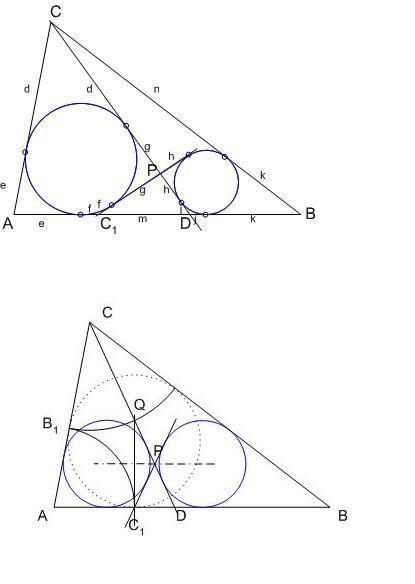
a) Legyen egyelőre ABC beírt körének érintési pontja AB-n C* . C* az az AB szakaszon lévő pont, melyre az A-tól és B-től mért távolságok különbsége ugyanakkora, mint C-re. Ennek igazolásához elég a csúcsokból a beírt körhöz húzható érintőszakaszok s-a és s-b kifejezéseire hivatkozni. Megmutatjuk, hogy ez C1-re is igaz, tehát C*=C1. Igazoljuk, hogy BC1–AC1=BC-AC , vagyis [BC1–AC1]–[BC-AC]=0 . Az ábrán a kisbetükkel jelölt egyenlő érintőszakaszokkal, valamint n=d+g+h és j+m=f+g+h felhasználásával [(k+j+m)–(e+f)]–[(k+n)-(d+e)]=[j+m-f]-[n-d]=[g+h]-[g+h]=0
b) Ennek alapján megállapíthatjuk, hogy van olyan A és B fókuszú hiperbola, mely C-n és C1-en is áthalad. A fenti képletet átrendezve [BC-BC1]–[AC–AC1]=0 , ami viszont azt jelenti, hogy van olyan C és C1 fókuszú hiperbola, mely A-n és B-n is áthalad. Erről kell belátni, hogy P-n is áthalad, vagyis [PC-PC1]–[AC–AC1]=0 . Az ábra érintőszakaszaival [(d+g)-(g+f)]–[(d+e)–(e+f)]=[d-f]–[d–f]=0 . A háromszögbe eső parabolaív minden P’ pontja kiadódik P-nek, ha D-t CP’ és AB metszéspontjának választjuk.
c) A két kör közös belső érintői szimmetrikusak a két kör centrálisára, a centrális felezi a CPC1 szöget, tehát érintője a hiperbolának. Egyenlő sugarak esetén a centrális párhuzamos AB-vel.
d) Visszavezettük a feladatot adott hiperbola adott irányú érintőjének és a P érintési pontnak a szerkesztésére. Tekintsük a hiperbolát mint az F1 középpontú vezérkört érintő és F2-n áthaladó körök középpontjának mértani helyét. F2-nek a P-beli érintőre vett F2’ tükörképe a vezérkör és a PF1 egyenes metszéspontja, F2F2’ merőleges az érintőre. A szerkesztés: Húzzunk F2-n át merőlegest egy érintőirányú egyenesre, ennek a vezérkörrel alkotott (egyik) metszéspontja F2’ , F2F2’ felező merőlegese az e érintő, e és F1F2’ metszéspontja a P érintési pont. Feladatunkban A a hiperbola pontja, az A körüli, C1-en áthaladó kör és az AC szakasz B1 metszéspontja rajta van a C körüli vezérkörön. Az ABre C1-ben emelt merőleges és a C körüli CB1 sugarú kör (egyik) metszéspontja legyen Q . A D pont CQ és AB metszéspontjaként adódik.
Ehhez a szerkesztéshez most már a hiperbola felhasználása nélkül is eljuthatunk. Ha a két kör sugara egyenlő, akkor közös belső érintőik tükrösek az AB -val párhuzamos centrálisra. Legyen Q a PC szakasznak az a pontja, melyre PQ=PC1. PQC1 egyenlőszárú háromszög C1Q alapja merőleges AB-re, Q rajta van az AB -re C1-ben emelt merőlegesen. Másrészt CQ=PC–PC1=AC–AC1 . Az AC szakaszra ráforgatva az AC1 távolságot a végpont legyen B1 . CB1=AC–AC1 . Q rajta van a C körüli CB1 sugarú körön, innen a szerkesztés a fenti.
|
 |
| Előzmény: [1422] BohnerGéza, 2010-06-03 16:31:30 |
|
|
| [1428] BohnerGéza | 2010-06-05 13:01:10 |
 Felhasználandó a 168. feladatban:
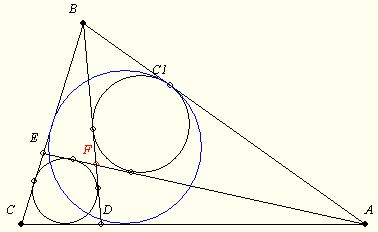
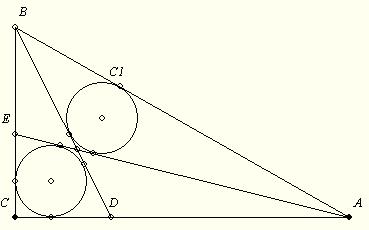
169. feladat: Az ABC háromszög AC illetve BC oldalán vegyük föl a D illetve E pontot úgy, hogy az AEC és BCD beírt köre azonos legyen: k1. Az AE és BD metszéspontja legyen F. Jelölje k2 az ABF beírt körét, érintse ez C1-ben AB-t. Igazoljuk, ha a CA-n mozgatjuk D-t (E és F megfelelően mozog), akkor C1 nem mozog. (Az ABC beírt körének pontja.)
|
 |
| Előzmény: [1427] BohnerGéza, 2010-06-05 12:53:18 |
|
| [1427] BohnerGéza | 2010-06-05 12:53:18 |
 Valóban! Pontosítva az [1406]-ban említett AD-feladatot:
168. feladat: Az ABC C-nél derékszögű háromszög AC illetve BC oldalán vegyük föl a D illetve E pontot úgy, hogy az AEC és BCD beírt köre azonos legyen: k1. Az AE és BD metszéspontja legyen F. Jelölje k2 az ABF beírt körét.
Fejezzük ki az ABC oldalai segítségével k1 sugarát, ha egyenlő a k2-ével!
|
 |
| Előzmény: [1424] HoA, 2010-06-05 09:01:13 |
|
|
| [1425] BohnerGéza | 2010-06-05 11:26:21 |
 167. feladat: Tekintsük az AFG háromszög k körülírt és C középpontú beírt körét. Legyen B a k tetszőleges pontja, a B-ből a beírt körhöz húzott érintők messék k-t még D-ben illetve E-ben. Igazoljuk, hogy DE érinti a beírt kört, azaz AFG és BDE beírt köre azonos.
Az [1409]- ben lévő 165. feladat bizonyításához elég megmutatni: Ha B-t k és AC másik metszéspontjának vesszük, szimmetria miatt elég belátni, hogy B egyenlő távol van F-től és C-től.
|
| Előzmény: [1409] HoA, 2010-04-23 17:24:22 |
|
|
|
| [1422] BohnerGéza | 2010-06-03 16:31:30 |
 A B.4269 feladattal kapcsolatban keletkezett a hozzászólás. Érdemes a "Lejárt határidejű KÖMAL feladatokról" című téma 552. hozzászólását is megnézni.
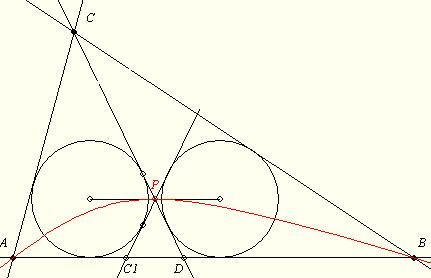
Az ABC háromszög AB oldalán mozgatjuk a D pontot. Az ADC és DBC beírt körének másik (nem CD) közös belső érintője AB-t a C1-ben metszi. A két belső érintő metszéspontja P. Mutassuk meg a következőket:
165. feladat: a.) Igazoljuk, hogy C1 nem függ D-től! (ABC beírt körének pontja)
b.) Igazoljuk, hogy a P pontok halmaza a C és C1 fókuszú és A-n átmenő hiperbola A-n (és B-n) átmenő ágának a háromszögbe eső része!
c.) Igazoljuk, hogy a két kör sugara akkor egyforma, ha a hiperbola P-ben húzott érintője párhuzamos AB-vel!
d.) A fentiek alapján szerkesztendő az a D, melyre a két kör sugara egyenlő!
|
 |
|
| [1421] kuklic | 2010-06-01 22:03:10 |
 Nagyon szépen köszönöm :) Elég jó vagy :D ezt magamtól nem biztos, hogy megláttam volna :)
|
|
| [1420] HoA | 2010-06-01 17:01:37 |
 A négy hasonló derékszögű háromszögből is szépen kijön, de talán a legegyszerűbb, ha észrevesszük, hogy az A1 -nél és B1 -nél lévő derékszögek miatt A1 és B1 rajta van AB Thálesz-körén, így ABA1B1 húrnégyszög, a szelőtétel éppen a kívánt egyenlőséget adja.
|
| Előzmény: [1419] kuklic, 2010-06-01 16:38:56 |
|
| [1419] kuklic | 2010-06-01 16:38:56 |
 Hello mindenki Egy kis segítséget kérnék. Ezzel a feladattal elakadtam:
Az ABC hegyesszögű háromszög A-ból induló magasságvonalának BC-vel való metszéspontja A1, B-ből induló magasságvonalának AC-vel való metszéspontja B1, magasságpontja M. Igazolja, hogy AM*MA1=BM*MB1!
|
|
| [1418] Hajba Károly | 2010-04-29 00:24:00 |
 Én egy kicsit másképpen oldottam meg, de HoA ábráját felhasználva már könnyebben megérthető.
A belső ötszög belső szögei: 5*180-360 = 540. Azaz az ötszögön belül kijelölsz egy pontot és 5 háromszöget képezel az öt pontból 2-2 szomszédos pont ill. a központi pont segítségével. Ez az öt háromszög teljesen kitölti a belső ötszöget. Az öt háromszög belső szögeinek összegéből levonod a központi ponthoz tartozó 360 fokot és így kapod az ötszög belső szögeinek összegét. Eddig talán nem is volt újdonság.
A külső szögeinek összegét úgy kapjuk, hogy az öt pont teljes szögeiből levonjuk a belső szögeket. 5*360-540 = 1260.
Most a belső ötszög külső oldalára 5 háromszöget illesztünk úgy, hogy épp a kívánt csillagötszöget adja ki. Itt a háromszögek belső 2-2 szögei részei az ötszög külső szögei tartományának. S közöttük épp a csúcsszög miatt épp a belső szög a különbség. Azaz, ha az ötszög külső szögeinek összegéből levonom a belső szögeinek összegét, akkor a háromszögek a belső ötszöggel érintkező 2-2 szög összegét kapjuk.
Vagyis ha az 5 háromszög szögösszegéből levonjuk a belső ötszög külső szögeit és hozzáadjuk a belső szögeit, akkor épp a csúcsszögek összegét kapjuk.
5*180 - 1260 + 540 = 180
Ha lesett a tantusz vagy kisült az isteni szikra, akkor már egyszerűbb, mint ahogy most leírtam.
|
| Előzmény: [1415] Cseri, 2010-04-27 23:46:12 |
|
|
| [1416] HoA | 2010-04-28 13:36:46 |
 Megoldásod annyiban vázlat, hogy abból, hogy a két háromszög beírt körének C a középpontja, még nem következik, hogy a hatszögbe kör írható, csak akkor, ha azt is igazoljuk, hogy a háromszögek beírt köreinek egyenlő a sugara - a beírt körök egybeesnek.
|
| Előzmény: [1414] lorantfy, 2010-04-27 21:33:10 |
|
| [1415] Cseri | 2010-04-27 23:46:12 |
 Üdvözlök mindenkit!
En egy uj vendeg vagyok ezen a weboldalon. Es lenne egy kerdesem. Esetleg valaki tudna nekem segiteni??!! Egy nem szabalyos csillagötszögröl ( pentagramma ) van szo. Be kell bizonyitani, hogy az öt csillagcsucsban levö szögeinek összege 180 fok. Ezt a szabalyos csillagötszögben be tudom bizonyitani,de a nem szabalyosban nem. Van esetleg valakinek ötlete?? Segitsegeteket elöre is köszönöm. Cseri Nemetorszagbol
|
|
| [1414] lorantfy | 2010-04-27 21:33:10 |
 Megoldásvázlat a 165.höz: A k körben AD és AE ívek valamint a BG és BF ívek egyenlők, mert a k1 illetve a k2 kör vágja ki őket. Így az AB húr az AFG és BDE háromszögben is szögfelező. FAC szög=GAC szög és AB a k2 körnek is szimmetria tengelye, így azonos íveket vág ki a k2 körből. Ez már bizonyítja, hogy GC is szöfelező, így C lesz az AFG háromszög beírt körének középpontja. Hasonlóan a másik, BDE háromszögre is, vagyis az említett hatszögnek is beírt köre. Ahogy lesz időm rajzolok egy ábrát. Jó példa! Köszönet érte!
|
| Előzmény: [1409] HoA, 2010-04-23 17:24:22 |
|
| [1413] Rozali | 2010-04-26 08:25:08 |
 Szia! Nagyon szépen köszönöm a segítséget !! Így már menni fog remélem!
|
|
| [1412] Tauthorne | 2010-04-25 16:18:50 |
 Bocsi, előző üzenetben véletlenül elírtam a legvégét: 7x+5y=-13 az egyenlete
|
|
| [1411] Tauthorne | 2010-04-25 16:14:57 |
 Szia! Mivel merőleges az adott egyenesre, ezért annak normálvektora (5,-7) az pont jó lesz a keresett egyenes irányvektorának. Az irányvektoros egyenlet pedig: v2x0-v1y0=v2x-v1y ,beirva a számokat: (-7)*(-4)-5*3=-7x-5y tehát:7x+5y=43
|
|
| [1410] Rozali | 2010-04-25 13:46:24 |
 Sziasztok! Megcsinálná ezt valaki nekem? Adjuk meg annak az egyenesnek az egyenletét, amely merőleges az 5x-7y=-17 egyenletű egyenesre,és átmegy a P(-4;3) ponton!
és ha kérhetem magyarázza is el mert lemaradtam és nem értem!!!!!!
Előre is nagyon köszi holnapra kellene!
|
|
| [1409] HoA | 2010-04-23 17:24:22 |
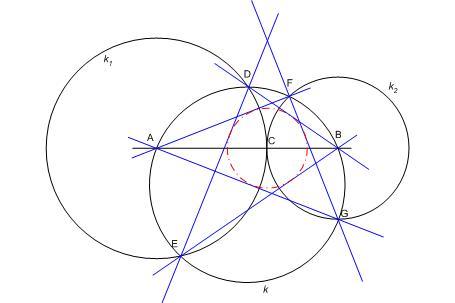
 Javaslat a 165. feladatra:
A k kör AB húrjának belső ponja C . Az A középpontú, C-n áthaladó k1 kör és k metszésponjai D és E, a B középpontú, C-n áthaladó k2 kör és k metszésponjai F és G . Bizonyítsuk be, hogy az AF , AG, BD , BE , DE és FG egyenesek által határolt hatszögbe C középpontú kör írható.
|
 |
|
|
| [1407] HoA | 2010-04-23 14:47:56 |
 1) Ha F a BC oldal belső pontja, akkor AF és BC metszéspontja F. Nem AF és BE metszéspontjáról van szó?
2) Ekkor viszont CFME nem lehet húrnégyszög, hiszen C-nél derékszögű, tehát M-nél is derékszögűnek kéne lennie, de a definíció szerint M a háromszög belső pontja és így az AB feletti Thálesz-körnek is belső ponja, vagyis FME szög = AMB szög > 90 fok. Mivel belé írható körről írsz, nem inkább érintőnégyszög?
|
| Előzmény: [1406] m2mm, 2010-04-23 14:29:17 |
|
| [1406] m2mm | 2010-04-23 14:29:17 |
 Tegnap volt kitűzve Arany Dánielen a következő(nem szó szerint ez volt a szöveg): Egy ABC C-ben derékszögű háromszög AC oldalának E, BC oldalának F belső pontja, AF és BC metszéspontja M. CFME húrnégyszög, a belé írható körének sugarának nagysága megegyezik AMB háromszög beírt körének sugaráéval. Fejezzük ki a háromszög oldalaiból a körök sugarának nagyságát.
|
|
|
| [1404] m2mm | 2010-04-06 18:47:47 |
 Üdv!
Egy egységsugarú körbe írt szabályos n-szög egyik csúcsát összekötjük az összes többivel. Bizonyítsuk be, hogy e szakaszok hosszainak szorzata éppen n.
|
|
| [1403] HoA | 2010-03-30 16:50:55 |
 Két megjegyzés:
1) Jogos az észrevétel, a kitűzés így lett volna korrekt: Adott két szakasz, a és b , b>0 , 0 a a b ... b ...
2) Vegyük észre, hogy a jobboldalt  függvényének q=f( függvényének q=f( ) tekintve az szimmetrikus a ) tekintve az szimmetrikus a  =22,5o;q=1/2 pontra, vagyis f(45o- =22,5o;q=1/2 pontra, vagyis f(45o- )=1-f( )=1-f( ) , ami BohnerGéza megoldásában is tükröződik. ) , ami BohnerGéza megoldásában is tükröződik.
Ez és a nevezőben szereplő 1+tg( ) talán indokolják, hogy a kifejezést tg( ) talán indokolják, hogy a kifejezést tg( ) és tg(45o- ) és tg(45o- ) szerepeltetésével alakítsuk át. ) szerepeltetésével alakítsuk át.
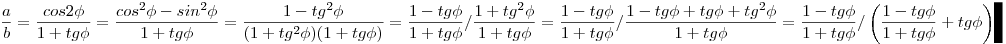
, amiből a.tg =(b-a).tg(45o- =(b-a).tg(45o- ) . Ennek alapján a szerkesztés: Vegyük fel a b hosszúságú AB szakaszt, A-ból B felé mérjük rá az a hosszúságú AT szakaszt. T-ben emeljünk m merőlegest AB-re, ennek T-től különböző pontja legyen C. Az ABC ) . Ennek alapján a szerkesztés: Vegyük fel a b hosszúságú AB szakaszt, A-ból B felé mérjük rá az a hosszúságú AT szakaszt. T-ben emeljünk m merőlegest AB-re, ennek T-től különböző pontja legyen C. Az ABC A-nál lévő szöge megfelel A-nál lévő szöge megfelel  -nek, ha a B-nél lévő szög 45o- -nek, ha a B-nél lévő szög 45o- , vagyis ha C-nél 135o-os szög van. C tehát m és az AB szakasz 135o-os látószögű körívének metszéspontja. , vagyis ha C-nél 135o-os szög van. C tehát m és az AB szakasz 135o-os látószögű körívének metszéspontja.
Hogyan kapcsolódik a fenti átalakítás a B. 4244 feladathoz?
|
| Előzmény: [1390] BohnerGéza, 2010-03-16 13:03:46 |
|
|
| [1401] Hajba Károly | 2010-03-21 22:04:33 |
 A könyvet a Typotex 2001-ben újra kiadta, de már elfogyott. Egy részét e-könyv formájában be lehet szerezni vagy antikváriumban kutakodni.
Ha küldtök címet, beszkennelem a feladatot és a megoldást.
|
|
| [1400] Róbert Gida | 2010-03-21 17:58:54 |
 A körös és a félsíkos példa a 40. Körre az optimális d, félsíkra 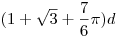 , ez utóbbi bizonyítás nélkül. (d a kör átmérője, illetve másiknál a félsík és a turista távolsága legfeljebb d). , ez utóbbi bizonyítás nélkül. (d a kör átmérője, illetve másiknál a félsík és a turista távolsága legfeljebb d).
|
| Előzmény: [1398] HoA, 2010-03-21 09:36:06 |
|
|
| [1398] HoA | 2010-03-21 09:36:06 |
 A téma iránt érdeklődőknek javaslok két magyar nyelvű anyagot:
Tóth Gábor: Bellman feladata KÖMAL 1982. 7. szám 53. oldal
és az ebben hivatkozott
Skljarszkij-Csenov-Jaglom: Válogatott feladatok és tételek ... 2/2 Geometriai egyenlőtlenségek ... 40. feladat
Remélem, a fórum olvasói számára hozzáférhetőek. ( Nekem a könyvet nem sikerült megszereznem, ha egy bemásolás erejéig valakitől kölcsönkaphatnám, megköszönném )
|
| Előzmény: [1396] jonas, 2010-03-17 09:53:10 |
|
| [1397] HoA | 2010-03-17 16:27:31 |
 Igen, a probléma különböző alakú erdőkre ismert. Én azzal a változattal találkoztam először, ahol az erdő egy félsík és azt tudom, hogy a szélétől max. R méterre vagyok, de a határegyenes irányát nem tudom. Mi az a legrövidebb útvonal, amit követve ( tetszőleges kezdőirányban indulva ) biztosan kijutok az erdőből? Mint a hivatkozott cikk elejéből látható, a másik kivesézett eset a két, adott távolságú párhuzamos közötti erdősáv.
http://www.jstor.org/pss/4145038
|
| Előzmény: [1396] jonas, 2010-03-17 09:53:10 |
|
| [1396] jonas | 2010-03-17 09:53:10 |
 Ezt nem értem. Ha az erdő kör alakú, akkor elég 2R hosszan egyenesen előre mennik, és kijutsz. Érdekesebb lenne, ha mondjuk az erdő egy félsík, és felteszed, hogy a kezdeti állapotban legfeljebb R mélységig vagy benne.
|
| Előzmény: [1392] psbalint, 2010-03-16 22:51:13 |
|
| [1395] psbalint | 2010-03-16 23:58:07 |
 a körvonalon elindulás nekem nem jutott eszembe. ha jól számoltam, akkor a négyzetes esetre R(1+2gyök2), a szabályos háromszögesre pedig R(1+2gyök3) jön ki, szóval mindegyiknél jobb az R*pi. egyébként ez az R*pi csak egy (jó) ötlet, vagy bizonyított, hogy ez az optimális?
|
| Előzmény: [1394] BohnerGéza, 2010-03-16 23:32:35 |
|
| [1394] BohnerGéza | 2010-03-16 23:32:35 |
 [1392]: Jó lett volna, ha támpontként a szükséges utat a felvetett esetekhez megadtad volna. Egy egyszerű tipp: helyünkön átmenő R sugarú körön elindulva R-szer pí út alatt biztosan kiérünk.
|
| Előzmény: [1392] psbalint, 2010-03-16 22:51:13 |
|
|
| [1392] psbalint | 2010-03-16 22:51:13 |
 meg még eszembe jutott valami, amit valószínűleg itt olvastam, de nem találom. adott egy R sugarú erdő, amiben el vagyunk veszve. milyen útvonalat járjunk be, hogy bárhol is vagyunk az erdőben, kijussunk belőle (a legrövidebb út)? valaki tudja, hol lett ez a feladat tárgyalva? vagy a megoldást? én most utánagondolva csak addig jutottam, hogy berajzoltam a körbe egy négyzetet meg egy szabályos háromszöget, melyeknek 3 ill. 2 csúcsát érintve (a középpontjukból indulva) egy-egy jó úthoz jutunk, ahogy látom, és amelyek közül a négyzetes tűnik rövidebbnek. ez lenne a jó megoldás? miért? miért nem? hilfe!
|
|
| [1391] psbalint | 2010-03-16 21:53:51 |
 Egy feladat, kérdés, vagy valaki mondjon rá valamit: Rajzoljunk egy lapra egy S betűt, de úgy, hogy szép függőleges legyen, és két félkörből tevődjön össze, melyeknek az átmérője legyen 1 egység. Kössük össze az S betű legmagasabban fekvő pontját a szimmetriaközéppontjával, és ennek a szakasznak a felezőpontja legyen F. Elkezd lefelé csúszni a szakasz az S betűn úgy, hogy a fölső végpontja szép lassan a szimmetriaközéppontba halad, míg a másik végpont is végig az S betűn marad (a hossza végig 1 egység) és végül eléri az S betű alját. Milyen utat jár be az F?
|
|
|
| [1389] HoA | 2010-03-14 10:17:54 |
 A "Majd tökölgetek milliméter-papírral és egy körzővel" mondatból arra következtetek, hogy barátunk nem abban tévedett, hogy a kör legtávolabbi pontja van 22 cm-re, hanem abban, hogy a húr hossza 395 cm. Nem hinném, hogy 4 méteres milliméterpapíron dolgozna. Ezért inkább azt hiszem, a húr csak 395 mm és akkor a legtávolabbi kör-pont lehet 22 cm = 220 mm-re, hiszen az több, mint 197,5 mm. Az általad leírt megoldás menete természetesen ekkor is helyes, csak a számszerű eredmények lesznek mások.
|
| Előzmény: [1386] SmallPotato, 2010-03-07 23:37:22 |
|
|
| [1387] Tudorabb | 2010-03-08 03:23:07 |
 Ez igen! Egy valóban kapkodó kérdésből kibogarászni a tényleges kérdést is tudást igényel. A 22 cm jelentőségét valamilyen oknál fogva figyelmen kívül hagytam, így az Attilát is félrevezettem, amit nagyon sajnálok. Válaszod tökéletesen érthető és nagyon köszönöm.
Üdv. Péter
|
| Előzmény: [1386] SmallPotato, 2010-03-07 23:37:22 |
|
| [1386] SmallPotato | 2010-03-07 23:37:22 |
 Ha jól értelek, van egy kör, amelynek egy húrja 395 cm hosszú. Ez, mint Attila is írta, természetesen önmagában kevés a húrhoz tartozó középponti szög meghatározásához. (Ha belegondolsz, a kör átmérője lehetne épp 395 cm, ekkor a szög 180°, vagy mondjuk 2*395 cm, ekkor a szög 60° stb.)
Ha jól értelmezem a mondatodat, akkor a jelzett húr és a hozzá tartozó rövidebb körív felezőpontja közötti távolság 22 cm. Ekkor először kiszámíthatod a kör sugarát, abból szögfüggvénnyel a húrhoz tartozó középponti szöget és abból az ív hosszát. (Amit írsz, hogy a kör legtávolabbi pontja lenne 22 cm-re, az lehetetlen, hisz a legtávolabbi pont a kör középpontjának túloldalán van, de a kör sugara már önmagában minimum 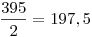 cm kell hogy legyen.) cm kell hogy legyen.)
A húr felére, a húr felezőpontját a körközépponttal összekötő szakaszra és a húr végpontjából induló sugárra felírt Pitagorasz-tétellel 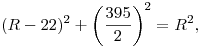 ahonnan R=897,51 cm; innen a középponti szög ahonnan R=897,51 cm; innen a középponti szög 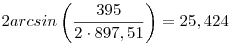 fok, amivel az ív fok, amivel az ív 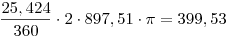 cm. cm.
|
| Előzmény: [1385] Tudorabb, 2010-03-07 17:42:32 |
|
| [1385] Tudorabb | 2010-03-07 17:42:32 |
 Kedves Attila! Amennyiben az 1383-as kérdésre válaszoltál is köszönöm szépen a segíteni akarásodat. Majd tökölgetek milliméter-papírral és egy körzővel. Apropó. Ha ez még segítene. A két pontot összekötő egyenes és a kör legtávolabbi pontja közti távolság ca. 22cm.
Minden jót kívánok, Péter
|
|
|
| [1383] Tudorabb | 2010-03-07 16:09:52 |
 Üdvözöllek Benneteket! Harmincöt éve érettségiztem és a jelek szerint sokat felejtettem. Kérdéseiteket és az arra adott válaszokat olvasgatva arra következtettem, hogy a legjobb helyen járok - Nálatok. Kérdés: A körből kivágok egy cikket. A sugarak és a kör metszéspontjainak egy egyenessel összekötött távolsága adott.( 395 cm )Milyen hosszú az ív, ill. a sugár? A számításotok menete érdekelne.
Segítségeteket előre is köszönöm, Péter
|
|
| [1382] HoA | 2010-02-27 23:06:29 |
 Felhasználjuk, hogy ha P az ABC háromszög belsejében vagy AB oldalán ( P != A ) fekszik, akkor AP + PB < AC + CB . Legyen ugyanis az AP és BC egyenesek metszéspontja Q. Ez a BC oldal belső pontja vagy B maga. Ekkor AP + PB <= AP + PQ + QB = AQ + QB < AC + CQ + QB = AC + CB.
A feladat szerint az AC és DE húrok és ívek egyenlőek, így a hozzájuk tartozó középponti szögek is. Legyen a kör középpontja O, D tükörképe az AB átmérőre D'. D'OB =DOB =DOB >=DOE >=DOE =COA =COA Így O a CD'B háromszög belsejében vagy ( ha E = B ) CD' oldalán fekszik, a fentiek szerint tehát CB + DB = CB + BD' > CO + OD' = 1 + 1 = 2 Így O a CD'B háromszög belsejében vagy ( ha E = B ) CD' oldalán fekszik, a fentiek szerint tehát CB + DB = CB + BD' > CO + OD' = 1 + 1 = 2
- Vegyük észre, hogy EB nélkül is teljesül az egyenlőtlenség!
- Egyenlőséget abban az elfajuló esetben kapunk, ha C = A és D = E = B
|
| Előzmény: [1375] m.atekoos, 2010-02-27 11:21:57 |
|
|
|
|
|
| [1377] Radián | 2010-02-27 19:10:36 |
 PC szakasszal mesd el az AB-t a kapott pont legyen Q. A CQ nem lehet egyszerre nagyobb AC és BC szakasznál is, mivel ha nem így lenne (felhasználva, hogy nagyobb oldallal szemben nagyobb szög van), akkor CAB szög> AQC szög és CBA>CQB szög egyszerre teljesülne,így CAB szög+CBAszög>AQC szög+CBQ szög=180 fok ez lehetetlen. Így kaptuk: PC<QC<CA v. CB <AB<PA+PB
|
| Előzmény: [1376] m.atekoos, 2010-02-27 15:23:16 |
|
| [1376] m.atekoos | 2010-02-27 15:23:16 |
 Itt egy feladat ami egy eszméletlen egyszerű de nekem sehogy se sikerült Segítene vki?
Tetszőleges 3szög belsejében felvesszük tetszőleges p pontot. Biz be, h a 3szög összes belső pontjára teljesül: AP+PB>PC Ilyenkor AB a leghosszabb oldal(ak egyike).
Előre is köszi a segítséget.
|
|
| [1375] m.atekoos | 2010-02-27 11:21:57 |
 Tudnátok segíteni?
Itt a feladat: egy egységnyi sugarú kör kerületére felvesszük ilyen sorrendben: A C D E B úgy hogy AB átmérő, tehát C,D,E egy félköríven helyezkedik el. Tudjuk hogy AC=DE. Biz be hogy CB+DB+EB>=2.
|
|
| [1374] sakkmath | 2010-02-25 10:40:53 |
 Kiegészítés a 162. feladathoz:
Nincs szükség számítógépes programra akkor, ha csak t1 = t2 bebizonyítására szorítkozunk és lemondunk a bonyolult területarány-képlet igazolásáról. Legyen ez a leszűkítés a 162/a feladat.
|
| Előzmény: [1355] sakkmath, 2010-01-06 16:51:48 |
|
| [1373] BohnerGéza | 2010-02-20 19:06:11 |
 Egy kicsit bővebb segítség:
A feladat a szerkesztések egyik alapgondolatát tartalmazza:
Adott két pont számára egy-egy vonal (egyenes vagy kör esetleg kúpszelet) és ismerünk egy geometriai leképezést, mely az első pontot a másodikba viszi.
Ekkor az első pont számára meglévő vonalra alkalmazva a leképezést, annak képe újabb vonal a második pont számára. A második már ismert pontra a leképezés inverzét alkalmazva, megkapjuk az első pontot.
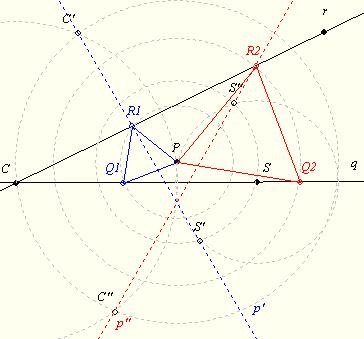
A mostani feladat szerkesztésénél figyelni kell, hogy két irányba forgathatunk! Az ábrán a q egyenes képeit a C és az S pontforgatásával kaptuk. A q'=C'S' a -60, a r"=C"S" a +60 fokos forgatás eredménye.
Amennyiben a qr szög 60 fok, ahogy a feladat feltétele mondja, akkor a q" párhuzamos lesz r-rel és csak egy megoldást kapunk. (A szerkesztés szempontjából mindegy, hogy P a szögfelezőn van vagy sem.)
|
 |
| Előzmény: [1369] laci777, 2010-02-20 14:00:57 |
|
|
| [1371] laci777 | 2010-02-20 14:53:13 |
 Köszönöm szépen - így leírva egyszerűnek tűnik. De nem állítanám, hogy térlátás nélkül evidens számomra a szögszár P pont körül elforgatása:(
Még egyszer köszönöm, kellemes hétvégét, szia: Laci
|
| Előzmény: [1370] jenei.attila, 2010-02-20 14:38:03 |
|
| [1370] jenei.attila | 2010-02-20 14:38:03 |
 Legyen A és B a háromszög másik két csúcsa, amelyek az egyik illetve másik szögszárra esnek. Mivel a háromszög szabályos, ezért az A-t a B-be egy 60 fokos P középpontú forgatás viszi. Tehát forgasd el P körül az egyik szögszárat 60 fokkal, és ahol az elfogatott szögszár elmetszi a másik szögszárat, ott lesz az egyik keresett csúcs. Ezt visszaforgatva, megkapod a másik csúcsot.
|
| Előzmény: [1369] laci777, 2010-02-20 14:00:57 |
|
| [1369] laci777 | 2010-02-20 14:00:57 |
 Sziasztok!
Tudna valaki segíteni?
Egy geometria szorgalmi feladattal gyűlt meg a bajom:
Vegyünk egy 60 fokos szöget, és a szögszáron belül egy tetszőleges P pontot, ahogy a P nem illeszkedik a 60 fokos szöget felező félegyenesre.
A feladat: szerkesszünk olyan szabályos 3-szöget, amelynek a P pont az egyik csúcsa, a másik két csúcs pedig a 2 szögszáron található (száranként 1-1).
Bármilyen segítséget előre is köszönök szépen.
Kellemes hétvégét kívánok mindenkinek!
Sziasztok: Laci
|
|
| [1368] HoA | 2010-01-14 11:45:29 |
 Elnézést, én sem gondoltam egészen végig. A 3 adott kör közül kettőnek az érintési pontjára vonatkozó inverzió igen egyszerű megoldást ad: két párhuzamos egyenest és egy kört érintő kört kell szerkeszteni. A gyakorlati kivitelezés különösen egyszerű, ha a k1 és k2 érintési pontja mint középpont körül az inverzió alapkörét úgy vesszük fel, hogy merőlegesen metssze k3-at. Ekkor k3 képe önmaga, és így a k3-at és az őt érintő két párhuzamost érintő kört kell szerkeszteni.
|
| Előzmény: [1363] S.Ákos, 2010-01-13 11:47:39 |
|
|
|
|
| [1364] HoA | 2010-01-13 12:06:17 |
 Az apró trükk ott van, hogy a legegyszerűbb megoldás nem használja ki, hogy a körök érintik egymást: Csökkentsük a körök sugarát a legkisebbik - legyen k3 - sugarával, ekkor a szerkesztendő k4 körrel koncentrikus k5 kört kell szerkeszteni, ami a csökkentett sugarú k1' és k2' köröket érinti és átmegy az O3 ponton. Az O3 középpontú inverzióval ez két kör közös érintőjének szerkesztésébe megy át. A Geometriai feladatok gyűjteményében a két kört kívülről érintő, adott P ponton áthaladó kör szerkesztésére szerepel egy inverziót nem használó módszer. Ott a körök külső hasonlósági pontját P-vel összekötő egyenesnek azt a Q pontját határozzuk meg először, amely szintén rajta van a szerkesztendő körön és így visszavezetjük a feladatot a két ponton átmenő, adott kört érintő kör szerkesztésére.
|
| Előzmény: [1362] Bosnyak, 2010-01-13 09:55:25 |
|
|
| [1362] Bosnyak | 2010-01-13 09:55:25 |
 Üdv mindenkinek! Volna egy problémám: Van három különböző tetszőleges sugarú kör ami érinti egymást. Annak a körnek a középpontját szeretném megszerkeszteni amely mind a három másik kört érinti,(belülről, a három kör által határolt területen) Remélem tud vki segíteni!
|
|
|
|
|
| [1358] BohnerGéza | 2010-01-10 15:27:53 |
 Az alábbi feladat felhasználható az OKTV - 2009-9010. II. kategória 3. feladatánál, de önmagában is jó feladat.
Használjuk ki a tg fv. tulajdonságait!
|
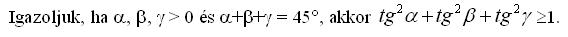 |
|
|
|
| [1355] sakkmath | 2010-01-06 16:51:48 |
 A következő feladatomat ajánlom megoldásra. (A megoldás végén valószínűleg elkerülhetetlen lesz számítógépes program használata. Ha ezért kissé kilógna e topicból, elnézést ... .)
(Kb.) 162. feladat: Egy hegyesszögű, nem egyenlő szárú háromszög területe T, oldalainak hossza a, b és c. A háromszög valamennyi magassági talppontján át húzzunk párhuzamost a talpponti oldallal szemközti csúcs szögfelezőjével. Tekintsük az így kapott egyeneseknek a szögfelező egyenesekkel alkotott metszéspontjait. Bizonyítsuk be, hogy e pontok két egyenlő területű háromszöget határoznak meg, melyek t1, illetve t2 nagyságú területére:
|
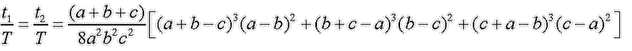 |
|
|
| [1353] laci777 | 2010-01-05 22:59:40 |
 Hát igen... Nekem meg épp ez a feladat volt elsőre (meg másodikra is...:P) megoldhatatlan.
Azért szerintem a túlzott szerénységre nincs okod:)
Köszönöm és további szép estét: Laci
|
| Előzmény: [1352] SmallPotato, 2010-01-05 22:47:32 |
|
|
|
| [1350] laci777 | 2010-01-05 22:43:06 |
 Kedves SmallPotato!
Nagyon szépen köszönöm az elegáns megoldást - bár lehet, itt ez a példa nem lehetett komolyabb kihívás.
Nem vettem észre a hasonló háromszögeket (sem)...
Még egyszer köszönöm!
További szép estét, szia: Laci
|
| Előzmény: [1348] SmallPotato, 2010-01-05 22:15:41 |
|
| [1349] HoA | 2010-01-05 22:31:51 |
 Ja, az más. Ha biztosra akarsz menni, használd [1343] lépéseit. Vagy kérdezd meg [1341] szerzőjét, ő hogy jutott erre az eredményre.
|
| Előzmény: [1346] Tym0, 2010-01-05 21:17:10 |
|
|
| [1347] SmallPotato | 2010-01-05 22:09:51 |
 Rajzold fel az elrendezésnek a kúp tengelyén átmenő síkmetszetét. Rajzold be a gömb két sugarát: a kúp alapkörének középpontjába irányulót és az alkotóra merőlegest. Az ábrádon két hasonló derékszögű háromszög lesz: az egyiknek a befogói a kúp alapkörének sugara és a kúp magassága, a másiknak a befogói az alkotóra merőlegesen berajzolt gömbsugár és az alkotónak a kúp csúcsa felé eső szelete. Írd fel a befogók arányát mindkét háromszögben.
|
| Előzmény: [1342] laci777, 2010-01-05 19:41:20 |
|
| [1346] Tym0 | 2010-01-05 21:17:10 |
 Bocs de nekem nincs se időm se türelmem bizonyítani. Én biztosra akarok menni. Elkezdtem csinálni. egyébként mástól kaptam. Remélem jó lesz.
|
| Előzmény: [1345] HoA, 2010-01-05 21:15:15 |
|
