| [435] jonas | 2006-06-09 22:53:35 |
 Indulj ki abból, hogy a négy sarokhoz négy különböző négyzetnek kell tartoznia, és azon kívül csak egy négyzeted van. Innentől három lehetőség van:
Az első kettőnél a nagy téglalap nem lehet négyzet, a harmadiknál a kis téglalapok. Persze ez nem precíz bizonyítás.
|
| Előzmény: [434] epsilon, 2006-06-09 22:21:08 |
|
| [434] epsilon | 2006-06-09 22:21:08 |
 Igen, ismerem a könyvet, nagyon kedves,és tanulságos! Sok helyen kerestem az 5-re egy szimpatikus bizonyítást, most meg az is felbuzdított, hogy a Kengurú egyik selejtezőjén feltették a kérdést, hogy hány darabra nem darabolható egy négyzet, és persze ott volt az 5 is, ez azt a gyanút keltette bennem, hogy ha ilyen helyen tippelés formájában adták föl, akkor csak kell lennie valamilyen egyszerű bizonyításnak! Hátha valaki találkozott ilyennel?!
|
|
| [433] jonas | 2006-06-09 21:42:58 |
 Igen, akárhány négyzetre feldarabolható. A bizonyítás megtalálható Reiman István könyvének 15. fejezetében. Ez azon áll, hogy bármely darabolásból kaphatsz egy 3-mal több négyzetté darabolást, ha az egyik kis négyzetet négy felé osztod, így elég megmutatni, hogy a négyzetet 4, 6, és 8 felé lehet vágni. Az 5 négyzetes esetre nem ad egyszerű bizonyítást.
|
| Előzmény: [432] epsilon, 2006-06-09 19:41:05 |
|
| [432] epsilon | 2006-06-09 19:41:05 |
 Helló! Nagyon szimpatikus feladat a négyzetnek az akárhány négyzetre darabolása, ez az "akárhány" természetesen 4 vagy több mint 5. Régóta felmerült bennem a kérdés, hogy van-e egyszerű bizonyítás arra, hogy egy négyzet nem darabolható fel 5 darab négyzetre? Ha van véleményetek, bizonyításotok szívesen várom! Üdv: epsilon
|
|
| [431] Csimby | 2006-06-05 01:23:39 |
 Szabó László: Konvex Geometria (Egyetemi jegyzet) Az ELTE TTK Déli épületében a 4. emeleten a geometria tanszék titkárságán lehet kapni, ha jól emlékszem kb. 500 ft.
|
| Előzmény: [430] tyuki, 2006-06-03 17:18:03 |
|
| [430] tyuki | 2006-06-03 17:18:03 |
 Szeretnélek bennetek megkérni arra, ha tudtok valami jó web-címet, amin találhatok összefüggő (hosszú) szöveget az affi-geometriáról, küldjétek el légyszi az e-mail címemre: nytuki@orangeportal.sk. Ha valami jó könyvet is tudtok ajánlani, azt is megköszönném. Köszi
|
|
|
|
| [426] Csimby | 2006-05-08 23:32:51 |
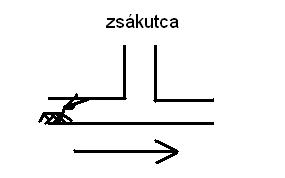
 Vagy inkább annyiféleképpen, ahányféle sorrendben n-2 db. hangya ki tud jönni egy járatból, ha a járat közepén található egy zsákutca (amiben tetszőlegesen sok hangya elfér de nem fér el egyszerre kettő menetiránnyal szemben) :-)
(Mind az n-2 db. hangyának ki kell jönni)
|
 |
| Előzmény: [425] jonas, 2006-05-08 23:05:06 |
|
| [425] jonas | 2006-05-08 23:05:06 |
 Hát igen, ehhez készült az ábra eredetileg.
Ugyanannyiféleképpen, mint ahány n-2 darab egyesből és n-2 darab mínusz egyesből álló sorozat van, aminek minden részletösszege pozitív. A bizonyítás levezethető az eredeti ábra postscript forrásából.
Ezzel, remélem, még nem árulok el sokat.
Elmondom majd a bizonyítást, ha érdekel valakit.
|
| Előzmény: [423] Csimby, 2006-05-08 21:49:32 |
|
|
| [423] Csimby | 2006-05-08 21:49:32 |
 75. feladat Egy szabályos n-szöget átlóival n-2 db. háromszögre daraboltunk. Hányféleképpen tehetjük ezt meg?
|
|
| [422] jonas | 2006-05-08 21:15:22 |
 Lehet, hogy sokan ismerik a következő feladatot.
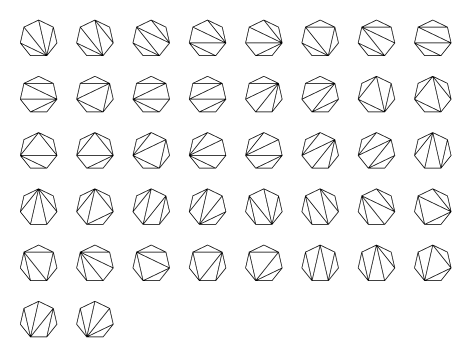
73. feladat. Ha egy 2n+1 oldalú szabályos sokszöget 2n-2 átlóval háromszögekre bontunk, akkor milyen határok között változhat a keletkező háromszögek közül a hegyesszögűek száma?
Segítségül itt egy ábra.
|
 |
|
| [421] Vonka Vilmos Úr | 2006-05-02 09:43:54 |
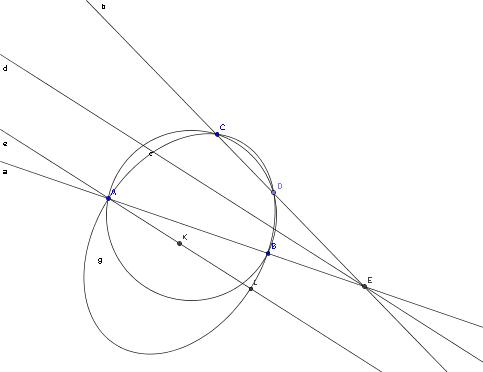
 Ez egy érdekes probléma. Nekem az a gyanúm, hogy ezen a projektív geometria nem tud segíteni. Ha ugyanis megadjuk pl az A, B, C, D pontokat, akkor ahogy kísérletezgettem GeoGebrában, úgy látom, előfordulhat, hogy akár 3 olyan ellipszis is van, aminek ezek pontjai, és A valamelyik tengely végpontja. Ha pedig 3 vagy több megoldás van, akkor hiába is keresünk jó szerkesztési eljárást. Persze az, hogy A a nagytengely, és nem a kistengely végpontja, az egy további szűkítés - ezt azonban projektív módon megfogni nehézkes, legfeljebb úgy tudom elképzelni, hogy valahogyan azt próbáljuk meg kihasználni, hogy a valós fókuszok egyenesén van rajta. Nekem ez sajnos nem sikerült.
Érdekes azonban, hogy ha A, B, C, D egy körön van, akkor már létezik nagyon egyszerű szerkesztési eljárás a tengelyek irányára: projektív eszközökkel ugyanis meg lehet mutatni, hogy akkor az AB, CD egyenesek szögfelezői párhuzamosak lesznek a keresett ellipszis tengelyeivel.
|
 |
| Előzmény: [418] Morci, 2006-04-26 12:00:31 |
|
| [420] Vonka Vilmos Úr | 2006-05-02 09:34:08 |
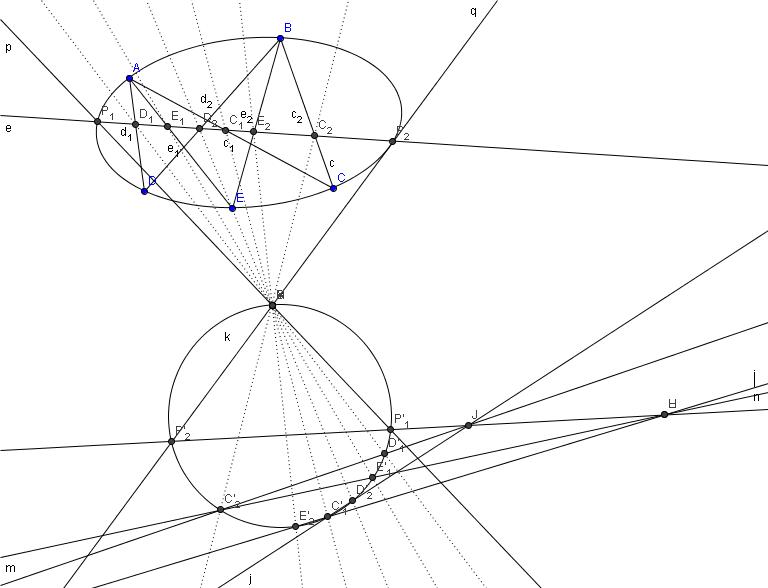
 Ha az ellipszis 5 pontját ismerjük, akkor projektív módon projektív sugársorok metszési alakzataként tudjuk előállítani. A sugársorok közötti projektív leképezést három megfelelő elempár határozza meg, így ha kiválasztjuk az adott A és B pontokat, mint tartópontokat, akkor az AC, AD, AE egyeneseknek megfelelő BC, BD, BE egyenesekkel megadtunk egy, a kúpszeletet meghatározó projektivitást. Ha a sugársorokat metszük az adott (e) egyenessel, akkor az e egyenesen projektív pontosorokat kapunk. Ebben a projektivitásban az önmagának megfelelő pont adja az egyenes és a kúpszelet metszéspontját. Így erre a projektivitásra a Steiner-féle kettőselem-szerkesztést alkalmazva kapjuk meg a keresett metszéspontokat. A Steiner-féle kettőselem-szerkesztésnél a síkon felvett tetszőleges körre annak egy tetszőleges pontjából rávetítjük a projektivitás megfelelő pontpárjait. Kiválasztva (az ábrán például) a C1' és C2' pontokat, rendre a C2', D2', E3' és C1', D1', E1' pontokat vetítve belőlük, perspektív sugársorokat kapunk. Ezen perspektivitás tengelye a kört a P1', P2' pontokban metszi, ezeket visszavetítve az (e) egyenesre, megkapjuk a keresett kettőspontokat.
|
 |
| Előzmény: [419] HoA, 2006-05-02 08:55:07 |
|
|
| [418] Morci | 2006-04-26 12:00:31 |
 Köszönöm a segítséget.
Átgondolom, kipróbálom, lehet lesz még kérdésem... nem ismerem mindegyik dolgot amit leírt, de rákeresgetek. (Nem matematikával-geometriával foglalkozom alapvetően.)
A probléma abban módosult, hogy kiderült nem 5 pont, hanem négy pont alapján kellene előállítani az ellipszist. A pontok közül 1 db az speciális azaz a nagytengely egyik végpontja. a többi 3 darab teljesen általános. Ebben kérnék segítséget. Próbáltam már kérdezgetni több felé, elvileg ez csak számítással oldható meg?
Üdv. Morci
|
| Előzmény: [407] Vonka Vilmos Úr, 2006-04-07 11:25:57 |
|
|
| [416] kenez | 2006-04-16 00:46:57 |
 Az informatikus kollégáktól kérnék segítséget. A probléma a következő. Van egy kockám, és szeretném azt megforgatni egy programmal. 1. kérdés : hogyan számítom ki a 8 csúcspont koordinátáit, ha elforgatom őket x,y,z tengely körül, és mi ennek a matematikai alapja(csak hogy értsem is hogy megy!), 2. kérdés : 3D - 2D leképezés módszere érdekelne nagyon részletesen. Ja és még valami. Van még ingyen letölthető szerkesztőprogi az Euklidesen kívül? Köszi mindenkinek! Kenéz
|
|
| [415] kenez | 2006-04-16 00:20:28 |
 Kösz, HoA, látod, néha még egy mondat is csodákra képes.... A helyzet az, hogy ebbe valóban nem gondoltam bele, mivel a szerkesztésnél annyira evidens volt, és látható, hogy nem gondoltam, hogy bizonyítani kéne. Mivel látványos volt a dolog, abba se gondoltam bele, csak akkor lehet trapéz, ha van egy párhuzamos oldalpárja. Hát nincs is neki. Ennyit erről. Kicsit jobban figyelni(Ezt magamnak mondom!).
|
|
| [414] HoA | 2006-04-15 22:45:14 |
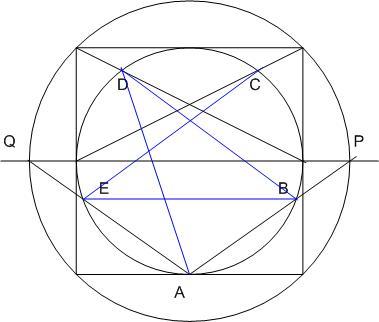
 Ábra (igaz, fejjel lefelé) mellékelve. Segítség: Miből gondolod, hogy pl. ABED húrtrapéz? AE és BD párhuzamosságát bizonyítani kellene.
|
 |
| Előzmény: [412] kenez, 2006-04-15 18:20:50 |
|
| [413] kenez | 2006-04-15 18:27:05 |
 Az ábrát elfelejtettem feltenni!
|
|
| [412] kenez | 2006-04-15 18:20:50 |
 Hello mindenkinek! Megoldottam egy feladatot, mindjárt le is írom a szövegét, a megoldásom viszont nem volt jó, nagyon szeretném, ha valaki megcáfolná az én megoldásomat, megmondaná, miért nem helyes. Köszönettel: Kenéz A feladat: Középkori építészek használták a következő szerkesztést a szabályos ötszög előállítására: Rajzoltak egy négyzetet, aztán megrajzolták a négyzet oldalaival párhuzamos szimmetriatengelyeket, majd a négyzet bele- és köréírt körét. A négyzet A oldalfelező pontját összekötötték a körülírt kör PQ átmérőjének végpontjaival. A négyzet beírt körét az AP és PQ szakaszok a B és E pontokban, a négyzet alsó felét adó KLMN téglalap átlói pedig a C és a D pontokban metszik. Az ABCDE pontok alkotják az ötszöget. Valóban szabályos ez az ötszög?
Az én megoldásom: Behúzva az AD BE CE BD szakaszokat, húrtrapézokat kapunk. Az ABED húrtrapézból : AB = ED. CEAB húrtrapézból : CB = AE. DABC húrtrapézból : AB = CD Eddig : AB = ED = CD EBCD húrtrapézból : CB = ED Tehát : AB = ED = CD = CB = AE Tehát ez egy olyan ötszög, amelynek minden oldala egyenlő, vagyis szabályos. Hol van a hiba a logikámban?
|
|
| [411] HoA | 2006-04-15 15:52:08 |
 [409] után a 68. - 70. - 71. feladatok tkp. a [388] -ban felvetett egyenlőtlenség szemléletes bizonyításai. Adjuk fel 72. feladat-ként az egyenlőtlenség trigonometriai - ábrát nem igénylő - bizonyítását.
Érdekességképpen megemlítem, hogy a tételre a Matematikai Versenytételek 1897(!!)-i egyik feladataként is rátaláltam. Igaz, ott az állítás nem ilyen éles, csak a
sin( /2) * sin( /2) * sin( /2) * sin( /2) * sin( /2) /2)  1/4 1/4
igazolását tűzték ki. A megoldás 1/8 -ra is szerepel.
|
| Előzmény: [409] BohnerGéza, 2006-04-12 00:44:01 |
|
| [410] Hajba Károly | 2006-04-12 07:38:44 |
 Kedves Géza!
Ha jól vettem az adást, akkor gyakorlatilag a szögek és térszögek közötti összefüggést, hasonlóságot az érintő ill. érintősík elfordulás, elmozdulás mértékében kell, lehet keresni.
Mégegyszer köszi a tájékoztatód.
|
| Előzmény: [405] Kós Géza, 2006-04-05 13:21:05 |
|
|
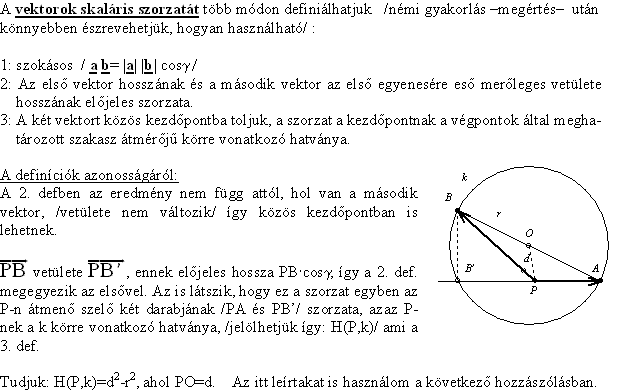
| [408] BohnerGéza | 2006-04-12 00:42:11 |
 A következő hozzászólásban használom az alábbiakat:
|
 |
|
| [407] Vonka Vilmos Úr | 2006-04-07 11:25:57 |
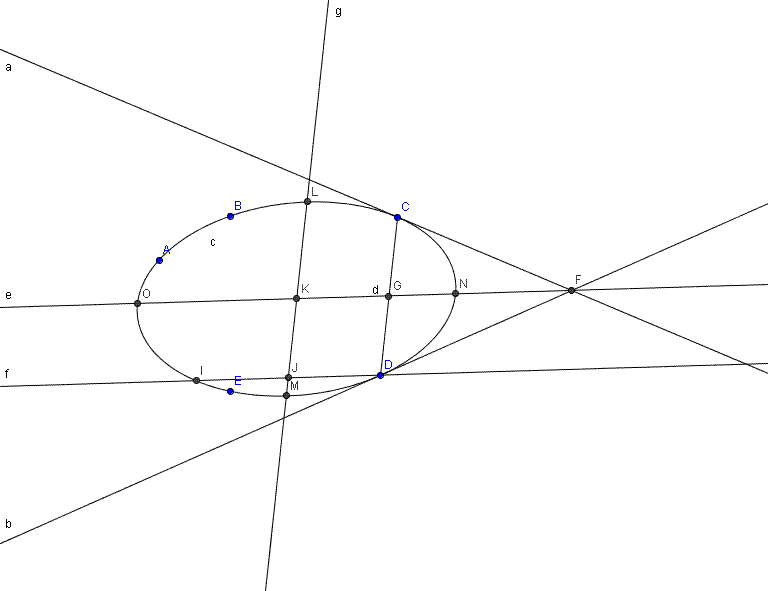
 Legyenek az ellipszis adott pontjai A, B, C, D, E!
1. A Pascal-tétel segítségével szerkeszthető pl. a C és D pontbeli érintő, ezek metszéspontját jelölje F!
2. Mivel F polárisa a CD egyenes, a CD irányához konjugált irányú átmérő áthalad az F ponton, valamint CD felezőpontján (G) is. Tehát FG (e) az ellipszis egy átmérő egyenese.
3. Legyen a D-n keresztül e-vel húzott párhuzamos egyenes f! A Pascal-tétel segítségével szerkeszthető f és az ellipszis másik metszéspontja (I). Az e-hez konjugált átmérő áthalad DI felezőpontján (J) és párhuzamos CD-vel: legyen ez a g egyenes.
4. A Steiner-szerkesztés segítségével megszerkeszthetőek e és g metszéspontjai az ellipszissel (LM, NO). Így megkaptuk az ellipszis egy konjugált átmérőpárját.
5. Egy konjugált átmérőpár ismeretében pl. Rytz-szerkesztéssel szerkeszthetőek az ellipszis tengelyei.
|
 |
| Előzmény: [406] Morci, 2006-04-06 21:59:18 |
|
| [406] Morci | 2006-04-06 21:59:18 |
 Üdv!
Segítséget szeretnék kérni. Netes keresőben itt dobott ki Pascal tétellel kapcsolatban infót, így gondoltam itt próbálok segítséget kérni.
Az a problémám, hogy egy ellipszis pontjai adottak, s nekem meg kell szekesztenem az ellipszist. A Pascal tétel alapján pontszámot tudok "bővíteni", illetve az itt talált ábra alapján még a nagytengely irányát is meg tudom határozni, viszont az ellipszis és a kör affin aránya ismeretlen, ezért nem lehet ezzel tovább lépni az ellipszis felől...
Van valamilyen módszer ellipszis szerkesztésére ha pár alkotó pontja adott csak?
Előre is köszönöm a segítséget!
|
|
|
| [405] Kós Géza | 2006-04-05 13:21:05 |
 Kedves Károly,
Már régóta tervezgetem, hogy egyszer majd kimerítőbben válaszolok a kérdésedre, de eddig nem jutottam hozzá. Lehet, hogy most is csak egy részét írom le.
A térben egy csomó dolog nem igaz úgy, mint a síkon, egyes dolgok pedig teljesen elvesznek. Pl. a síkon egy üres rácsháromszög, aminem a csúcsai rácspontok, de sem a kerületén, sem a belsejében nincsenek további rácspontok, mindig 1/2 területű. A térben a megfelelő állítás nem igaz, egy üres rácstetraéder térfogata akármilyen nagy lehet.
A szögek összegének létezik a térben megfelelője, de nincs szoros kapcsolata a csúcsoknál előforduló térszögek összegével. Ha például egy tetraédert kilapítasz úgy, hogy konvex négyszöggé fajul, a térszögek mindegyike 0-hoz fog tartani.
Ami a szögek összegének megfelel, az a görbület integrálja. A síkban egy egyszerű zárt töröttvonal esetén a külső szögek összege 2 , illetve egy kétszer folytonosan differenciálható egyszerű görbén a görbület ívhossz szerinti integrálja 2 , illetve egy kétszer folytonosan differenciálható egyszerű görbén a görbület ívhossz szerinti integrálja 2 . Ha a görbe/töröttvonal nem egyszerű, akkor az eredmény 2 . Ha a görbe/töröttvonal nem egyszerű, akkor az eredmény 2 -szer az irány körülfordulásainak száma. -szer az irány körülfordulásainak száma.
A térben egy elég sima, egyszerű zárt felületen a Gauss-görbület felszín szerinti integrálja mindig 4 . .
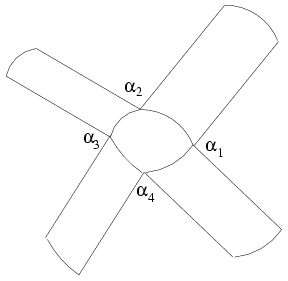
A poliédereket tekinthetjük sima felületek limeszének. pl. Minden élt lekerekítünk egy hengerpalásttal, a csúcsokat pedig gömbfelületekkel. (Most tekintsünk el attól, hogy ez nem mindig lehetséges, mondjuk szorítkozzunk a konvex poliéderekre.) A síklapokon és a hengerpalástokon a Gauss-görbület 0. A csúcsoknál a görbület integrálja a megfelelő gömbsokszög területe. A gömbsokszögeket összetolhatjuk egyetlen gömbbé, aminek a felszíne 4 . .
A gömbsokszögecskék területét másképp is kiszámolhatjuk.
Számoljuk össze egy csúcsnál a lapok szögeit. (Nem a lapsíkok közötti szögeket, hanem mindegyik lapnak az adott csúcsnál levő szögét.) Ha a szögek  1,..., 1,..., n, akkor a gömbsokszög szögei n, akkor a gömbsokszög szögei  - - 1,..., 1,..., - - n, a területe pedig 2 n, a területe pedig 2 -( -( 1+...+ 1+...+ n). Ha ezt az összes csúcsra kiszámoljuk és összeadjuk, akkor a csúcsok számát meg kell szoroznunk 2 n). Ha ezt az összes csúcsra kiszámoljuk és összeadjuk, akkor a csúcsok számát meg kell szoroznunk 2 -vel és ki kell vonnunk az összes lap összes szögének összegét. -vel és ki kell vonnunk az összes lap összes szögének összegét.
Legyen a csúcsok, élek, lapok száma C, E és L. Az egyes lapok éleinek száma legyen e1,...,eL. Ekkor persze e1+...+eL=2E, mert minden él két laphoz tartozik. Az i-edik lapon a szögek összege (ei-2) , az összes lap összes szögének összege tehát (e1-2) , az összes lap összes szögének összege tehát (e1-2) +...+(eL-2) +...+(eL-2) =(e1+...+eL-2L) =(e1+...+eL-2L) =(E-L)2 =(E-L)2 . .
A görbület integrálja a teljes felületen C.2 -(E-L)2 -(E-L)2 =(C-E+L)2 =(C-E+L)2 =4 =4 . .
A dolog egyrészt vicces, mert megjelenik a poliédertétel (C-E+L=2), ugyanakkor mindezt Gauss-görbület integrálása nélkül is tudtuk, és sem lap, sem térszögek nem jelentek meg...
|
 |
| Előzmény: [402] Hajba Károly, 2006-04-03 23:35:54 |
|
| [403] HoA | 2006-04-04 13:56:15 |
 A [388] egyenlőtlenség és a 68. feladat közötti kapcsolatról:
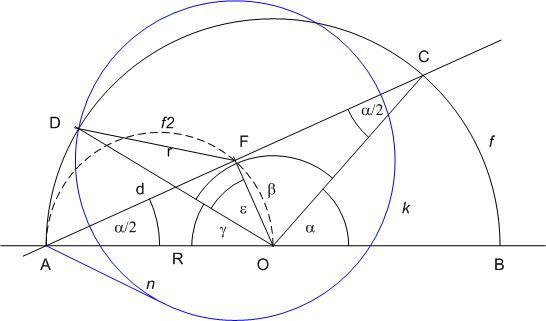
Legyen BOC  = = , COD , COD  = = , DOA , DOA  = = , , + + + + = = . Ekkor OAF . Ekkor OAF  = = /2 , DO = R ; FO = m = R*sin( /2 , DO = R ; FO = m = R*sin( /2), FA = d = R*cos( /2), FA = d = R*cos( /2), FOD /2), FOD  = = = = -( -( /2- /2- /2)= /2)= + + /2- /2- /2 /2
FD2=r2=DO2+FO2-2*DO*FO*cos =R2*(1+sin2( =R2*(1+sin2( /2)-2*sin( /2)-2*sin( /2)*cos /2)*cos ) )
n2=d2-r2=R2*(cos2( /2)-1-sin2( /2)-1-sin2( /2)+2*sin( /2)+2*sin( /2)*cos /2)*cos )=R2*(-2*sin2( )=R2*(-2*sin2( /2)+2*sin( /2)+2*sin( /2)*cos /2)*cos )= )=
2R2*sin( /2)*(cos /2)*(cos -sin( -sin( /2)) . /2)) .
A [388] egyenlőtlenségben válasszuk úgy a betűzést, hogy    teljesüljön és ennek megfelelően legyen D közelebb A-hoz mint C-hez. Ekkor teljesüljön és ennek megfelelően legyen D közelebb A-hoz mint C-hez. Ekkor  = = + + /2- /2- /2 /2  /2+ /2+ /2+ /2+ /2- /2- /2=0 , cos /2=0 , cos =sin( =sin( + + /2) , n2=2R2*sin( /2) , n2=2R2*sin( /2)*(sin( /2)*(sin( + + /2)-sin( /2)-sin( /2)) /2))
Felhasználva a sin(u+v) - sin(u-v) = 2*cos(u)*sin(v) azonosságot
n2=4R2*sin( /2)*cos(( /2)*cos(( + + )/2)*sin( )/2)*sin( /2)=4R2*sin( /2)=4R2*sin( /2)*sin( /2)*sin( /2)*sin( /2)*sin( /2) /2)
|
 |
| Előzmény: [388] BohnerGéza, 2006-03-14 12:02:36 |
|
| [402] Hajba Károly | 2006-04-03 23:35:54 |
 Üdv!
A Wolfram-on kicsit kutakodva ill. az SH Atlaszban találtam még néhány dolgot, de egy kicsit elgondolkoztam én is a témán. (Magad uram, ha szolgád nincsen.:o)
Ismert, hogy egy gömbháromszög területe 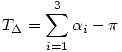 . Ezen minimális gömbi sokszöghöz adott szomszédos pontpárjukat egyesítve újabb háromszög illeszthető. Így tetszőleges n-sokszög állítható elő, akár konkáv is. Ezen sokszög területe, melyet nem nehéz belátni, . Ezen minimális gömbi sokszöghöz adott szomszédos pontpárjukat egyesítve újabb háromszög illeszthető. Így tetszőleges n-sokszög állítható elő, akár konkáv is. Ezen sokszög területe, melyet nem nehéz belátni, 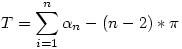
Ezen gömb középpontjából kiinduló és a sokszög pontjaira illesztett félegyenesek a pontok sorrendje szerint a félegyenesek közötti síkok által meghatározott térrész a T-vel arányos térszöget határoz meg.
A gömbi sokszög adott csúcspontjára illesztett és a gömböt érintő sík a csúcsba befutó két gömbi egyenes és gömbközéppont által meghatározott két síklapra merőleges. Ezért a két síklap által bezárt szög azonos a csúcsponti szöggel.
Fentiekből következik, hogy egy síkidom adott csúcspontjához tartozó szomszédos lapok által meghatározott szögek összege és a lapok által meghatározott térszög mértéke között szoros összefüggés áll fenn a fenti képlet szerint.
Újabb érdekes összefüggések adódnak egy idom lapszögeinek és térszögeinek összegei között, de erről később, ha addig valaki nem tesz be egy ezirányú összefoglaló linket. Mert biztos van erről irodalom, legfeljebb még nem bukkantam rá.
|
| Előzmény: [398] Lóczi Lajos, 2006-03-29 22:21:15 |
|
|
| [400] Hajba Károly | 2006-03-30 14:21:40 |
 Köszi. Amit nyelvtudás nélkül ki lehet belőle hámozni, azt eddig is sejtettem.
Gyakorlatilag az érdekelne, hogy a síklapú testek csúcsaihoz tartozó térszögek összege milyen szabályosságot mutat. Mennyire analóg ill. milyen módon analóg a 2D-s szabályokkal. 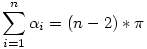 Egy-egy csúcshoz tartozó síkszögek és térszög között milyen összefüggések állnak fenn. Egy-egy csúcshoz tartozó síkszögek és térszög között milyen összefüggések állnak fenn.
Azt gyanítom, hogy azonos csúcsszámú testekhez nem feltétlenül azonos nagyságú térszög összeg tartozik. Talán a csúcshoz tartozó síkszögek valamiféle összesítése állandó, vagy esetleg a síklapok által közrezárt szögek összege?
|
| Előzmény: [398] Lóczi Lajos, 2006-03-29 22:21:15 |
|
| [399] BohnerGéza | 2006-03-30 08:02:53 |
 Köszönöm HoA-nak és Jenei Attilának a 68. ill. 70. feladatra adott megoldásait! Még eggyel bővítem a kapcsolódó feladatokat:
71. feladat: Az adott AB átmérőjű félkörön a 68. feladat ábrájának megfelelő sorrendben ([385] hozzászólás) helyezkedik el a C és D pont. Hol vannak ezek, ha a BC*CD*DA maximális?
|
|
|
| [397] Hajba Károly | 2006-03-27 13:21:05 |
 Üdv!
Egy kis elméleti fejtágításra lenne szükségem a térszögek terén. Az alapfogalmak (térszög, szteradián) meghatározásán kivül nem sok mindent ad ki a Kugli.
Előre is köszönök minden segítséget ill. magyarnyelvű linket.
|
|
| [396] HoA | 2006-03-24 14:34:56 |
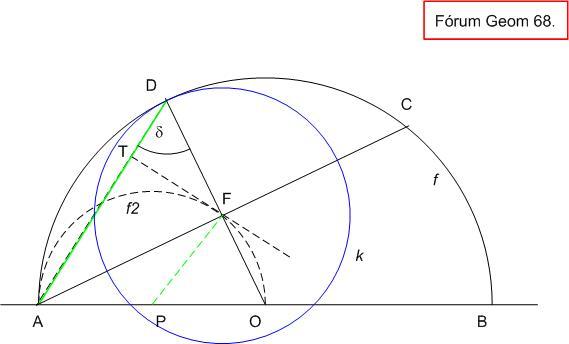
 Kedvet kapva Jenei Attilától egy cosinus tételes megoldásra, mégegyszer a 68. feladatról : Odáig, hogy k belülről érinti f-et ld. a 386-os hozzászólást. Legyen az f2 félkörív középpontja P. AD-t rögzítve n2=AF2-FD2=AD2-2*AD*FD*cos =AD(AD-2*FD*cos =AD(AD-2*FD*cos ) . Mivel D az f2 köríven kívül van, ) . Mivel D az f2 köríven kívül van,  hegyesszög, a kifejezés akkor a legnagyobb, ha DT=FD*cos hegyesszög, a kifejezés akkor a legnagyobb, ha DT=FD*cos , FD merőleges vetülete AD-re a legkisebb. Ez pedig akkor áll elő, ha FT az f2 körív AD-re merőleges érintője. De ekkor PF || AD, POF és AOD , FD merőleges vetülete AD-re a legkisebb. Ez pedig akkor áll elő, ha FT az f2 körív AD-re merőleges érintője. De ekkor PF || AD, POF és AOD  -ek hasonlóak, PF = PO -> AD = AO, vagyis AD az f félkörben sugár hosszúságú húr. -ek hasonlóak, PF = PO -> AD = AO, vagyis AD az f félkörben sugár hosszúságú húr.
|
 |
| Előzmény: [395] jenei.attila, 2006-03-22 11:48:06 |
|
| [395] jenei.attila | 2006-03-22 11:48:06 |
 A szóbanforgó érintési pont legyen E.
BE2=BD2-DE2=BD2-DC2=AB2-AD2-DC2
Ezért BE akkor maximális, ha AD2+DC2 minimális.
AD2+DC2=AC2+2*AD*DC*cos 
. Mivel AC állandó és cos  állandó és negatív AD*DC-nek kell maximálisnak lenni. Vagyis mivel sin állandó és negatív AD*DC-nek kell maximálisnak lenni. Vagyis mivel sin  állandó és pozitív az ADC háromszög területének kell maximálisnak lenni. Ez pedig akkor maximális, ha D az AC ív felezőpontja. Nem használtuk ki, hogy C az AB ív felezőpontja. állandó és pozitív az ADC háromszög területének kell maximálisnak lenni. Ez pedig akkor maximális, ha D az AC ív felezőpontja. Nem használtuk ki, hogy C az AB ív felezőpontja.
|
| Előzmény: [389] BohnerGéza, 2006-03-17 07:55:20 |
|
|
| [393] HoA | 2006-03-21 09:55:50 |
 A 70. feladat-ra van egy, a 68-ashoz hasonló trigonometriai megoldásom, ha nem lesz jobb, beírom. De szívesen látnék erre is meg a 68-asra is egy nem trigonometriait.
|
| Előzmény: [389] BohnerGéza, 2006-03-17 07:55:20 |
|
| [392] HoA | 2006-03-21 09:50:54 |
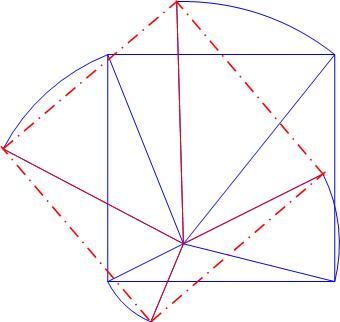
 Ha arra gondolsz, hogyan kell elforgatni egy négyzetet a síkjában fekvő adott pont körül adott szöggel - és ekkor mindegy, a pont a négyzeten belül vagy kívül van - egy megoldás az ábra szerinti: az adott pontból a négyzet csúcsaiba húzott szakaszok mindegyikét elforgatjuk az adott szöggel. Az új végpontok az elforgatott négyzet csúcsai.
|
 |
| Előzmény: [391] tothszivike, 2006-03-20 19:00:39 |
|
| [391] tothszivike | 2006-03-20 19:00:39 |
 Segítséget szeretnék kérni! Hogyan kell elforgatni egy négyzetet egy azon belüli ponton keresztül mert nekük az osztályban mindenkinek trapéz jött ki a tanárnő meg nem hajlandó megmutatni!
|
|
| [389] BohnerGéza | 2006-03-17 07:55:20 |
 A 384. hozzászólásban HoA által felvetett kérdés miatt alakult ki a következő feladat:
70. feladat: Az AB átmérőjű félkörív felezőpontja C. D az AC íven mozoghat. Mikor lesz leghosszabb a B-ből a D középpontú, C-n átmenő körhöz húzott érintőszakasz?
|
|
|
| [387] axbx | 2006-03-13 20:48:33 |
 Nem megy nékem az geometria..
|
|
| [386] HoA | 2006-03-10 16:17:31 |
 Köszönöm az ábrát.
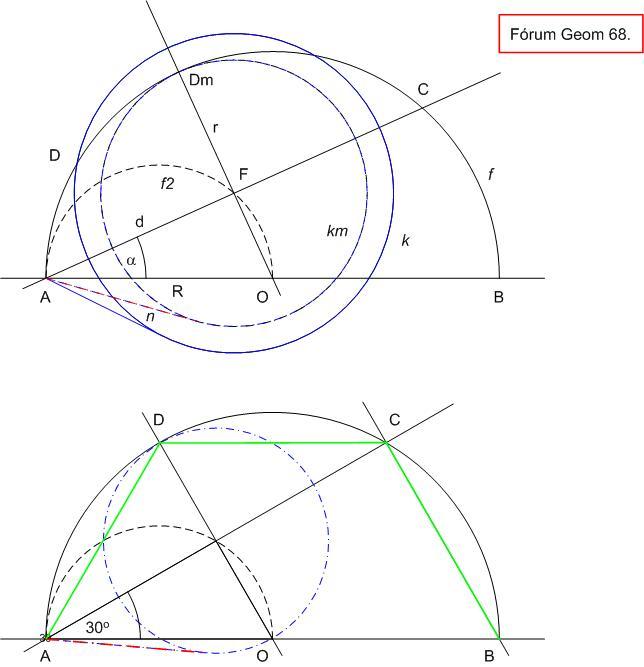
Legyen az AB átmérőjű f félkör középpontja O, sugara R. F rajta van f A-ból vett 1/2 arányú kicsinyítésén vagyis az AO átmérőjű f2 félkörön. n hossza A pont k-ra vonatkozó hatványának négyzetgyöke. Az AF távolságot d-vel, k sugarát r-rel jelölve n2=(d+r)(d-r)=d2-r2 . C-t - és ezzel F-et és d-t - rögzítve ez akkor a legnagyobb amikor r a legkisebb, vagyis amikor k belülről érinti f-et. Ekkor D az OF egyenes és f metszéspontja, jelöljük Dm-mel.
C-t az f félkörön mozgatva, C és F helyzetét a 0 és 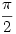 közé eső BAC = OAF = közé eső BAC = OAF =  szöggel jellemezve, mivel F rajta van OA Thalesz-körén szöggel jellemezve, mivel F rajta van OA Thalesz-körén
d=Rcos ,r=R(1-sin ,r=R(1-sin ) )
n2=R2(cos2 -(1-sin -(1-sin )2)=R2(cos2 )2)=R2(cos2 -1-sin2 -1-sin2 +2sin +2sin )=R2(cos2 )=R2(cos2 -cos2 -cos2 -sin2 -sin2 -sin2 -sin2 +2sin +2sin )= )=
=2R2(sin -sin2 -sin2 )=2R2(sin )=2R2(sin )(1-sin )(1-sin ) )
Ez pedig a számtani és mértani közép egyenlőtlenség miatt akkor a legnagyobb, ha sin =1-sin =1-sin =1/2 Ez a vizsgált tartományban =1/2 Ez a vizsgált tartományban  =30o -nál következik be. Így DOA szög = CBA szög = 60o , A, D, C és B pontok egy szabályos hatszög egymás utáni csúcsai. sin =30o -nál következik be. Így DOA szög = CBA szög = 60o , A, D, C és B pontok egy szabályos hatszög egymás utáni csúcsai. sin =1/2 -t helyettessítve =1/2 -t helyettessítve 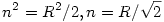
|
 |
| Előzmény: [385] BohnerGéza, 2006-03-09 20:26:52 |
|
|
| [384] HoA | 2006-03-09 17:53:28 |
 - Az én értelmezésemben a rögzített AB átmérőjű félköríven C és D csak ACDB vagy ADCB sorrendben lehetnek.
- F az AC szakasz vagy az AC ív felezőpontja?
|
| Előzmény: [382] BohnerGéza, 2006-03-09 12:15:40 |
|
|
| [382] BohnerGéza | 2006-03-09 12:15:40 |
 68. feladat: C és D a rögzített AB átmérőjű félköríven vannak ABCD sorrendben. Legyen F az AC felezőpontja, k az F középpontú, D-n átmenő kör és n az A-ból k-ig húzott érintőszakasz. Hol van C és D, ha n a lehető leghosszabb? Mekkora ekkor n? (AB-hez képest.)
|
|
| [381] hobbymatekos | 2006-03-08 14:48:24 |
 Sziasztok. Én úgy gondolom: a szabályos háromszög oldallapok súlypontjaiba a lapok területével azonos skalárok (mint tömeg pontrendszer) tömegközéppontjában lesz a tetraéder súlypontja. (Vagyis a statikai nyomatékok vektorainak bármely geometriai pontra számitott eredő nyomaték vektorának a súlypontba redukáltja nullvektor.)
|
| Előzmény: [378] BohnerGéza, 2006-02-23 23:30:05 |
|
| [379] axbx | 2006-02-27 16:34:28 |
 Már a véleményemet se mondhatom el.. (Fődmívelö) Azért nem vót szép, hogy bannoltak.
Na csak Az lenne a kérdésem, hogy hogyan kell bizonyítani a kör egyenletét?
|
|
| [378] BohnerGéza | 2006-02-23 23:30:05 |
 Azt hiszem, az előző feladat után természetesen adódik, az érdeklődés miatt is, ha a térbeli analóg feladatot is kitűzöm.
67. feladat: Hol van a homogén vékony lemezből álló ABCD tetraéderhéj fizikai értelemben vett súlypontja.
|
|
|
|
|
|
|
| [372] jonas | 2006-02-23 22:45:46 |
 Akkor a keresett pontot úgy is megkaphatjuk, hogy az eredeti háromszög beírt körének középpontját -1/2-szeresére nagyítjuk az eredeti háromszög súlypontjából, vagy úgy is, hogy az eredeti háromszög csúcsait b+c,c+a,a+b arányban súlyozzuk. (Hol is van az a háromszög-nevezetes-pont-katalógus?)
|
| Előzmény: [369] jonas, 2006-02-23 22:34:34 |
|
| [371] lorantfy | 2006-02-23 22:41:25 |
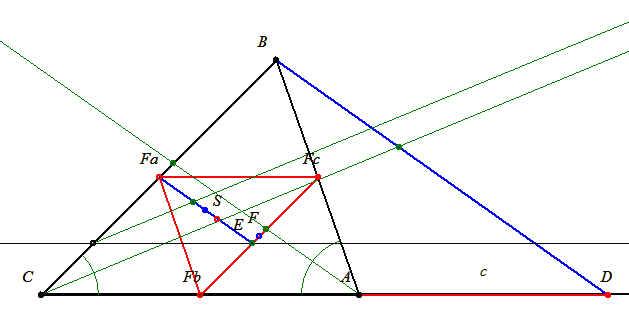
 Az FcEFa háromszög hasonló CDB háromszöghöz, így az Fc-ból induló szögfelező a szemközti oldalt éppen (b+c)/a arányban osztja. Tehát S pont az FaFbFc háromszög szögfelezőinek metszéspontja, vagyis a beírt körének középpontja.
|
 |
| Előzmény: [369] jonas, 2006-02-23 22:34:34 |
|
|
| [369] jonas | 2006-02-23 22:34:34 |
 Azzal hogy az egyes oldalakat drótból készítenénk el, egyenértékű, ha az oldalak felezőpontjába rakunk az oldalhosszal arányos súlyokat, és ezeknek a súlypontját keressük. Na de a középvonal-háromszög oldalai fele olyan hosszúak, mint az eredeti háromszög megfelelő oldalai. Ezért a középvonal-háromszög csúcsait kell súlyozni a szemközti oldalakkal, így pedig a beírt körét kapjuk.
|
| Előzmény: [368] jonas, 2006-02-23 22:29:56 |
|
|
| [367] jonas | 2006-02-23 22:26:52 |
 Nézzük csak. Nevezetes pont. Egy nagyon hosszú egyenlőszárú háromszögnek a felénél van, tehát nem lehet a magasságpont, a beírt kör középpontja, a súlypont vagy a Feuerbach kör középpontja, csak a körülírt kör középpontja lehetne. Az viszont nyilván nem lehet, mert az a háromszögön kívül is lehet, a drót súlypontja viszont nem. Akkor kevésbé nevezetes pont lesz.
|
| Előzmény: [362] BohnerGéza, 2006-02-23 08:15:11 |
|
| [366] lorantfy | 2006-02-23 22:22:21 |
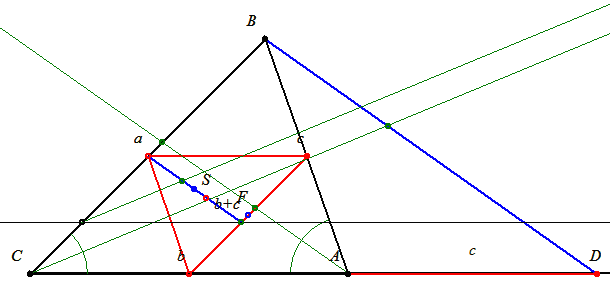
 Szerkesszük meg ezt a speciális súlypontot!
Az oldalfelező pontokba helyezzünk az oldalak hosszának megfelelő tömegpontokat.
A 'bc' szakaszt c/b arányban kell osztanunk. A szögfelező b/c arányban osztja. Tükrözzük ezt a pontot a szakasz felezőpontjára és helyezzünk ebbe a pontba b+c tömegpontot.
Már csak az 'a b+c' szakaszt kell (b+c)/a arányban felosztani. A C-ből induló szögfelező BD szakaszt a/(b+c). Ehhez hasonló kisháromszöget alakítunk ki és ebben a szögfelező azonos arányban osztja a szemközti oldalt.
Már csak tükröznünk kell ezt a pontot a felezőpontra. Ez lesz az S súlypont. Remélem idáig jó!
|
 |
| Előzmény: [362] BohnerGéza, 2006-02-23 08:15:11 |
|
|
|
|
| [362] BohnerGéza | 2006-02-23 08:15:11 |
 66. feladat: Hol van egy homogén, vékony drótból készült ABC háromszögnek a fizikai értelemben vett súlypontja? ( ABC-hez kapcsolható nevezetes pont lesz.)
|
|
|
| [360] qer | 2006-02-17 18:55:53 |
 Megoldás a 65. feladatra: leírva nincs szögfüggvény, de végülis ott van...
Legyen AB az n-szög egyik oldala, a kör sugara egységnyi. Ekkor AOB szög 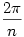 , AB-t jelöljük a-val, OF-t m-mel. , AB-t jelöljük a-val, OF-t m-mel.
Nyílván 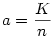 , , 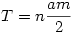 . Az . Az 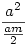 hányadost átalakíthatjuk a következő alakra: hányadost átalakíthatjuk a következő alakra: 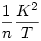 . Tehát a bizonyítandó egyenlőtlenséget így is írhatjuk: . Tehát a bizonyítandó egyenlőtlenséget így is írhatjuk: 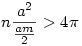 . .
Kis átalakítások után a következő alakra hozható az egyenlőtlenség: 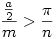 . .
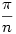 az AOF (vagy A'OF') szöggel egyenlő. Mivel az AOF (vagy A'OF') szöggel egyenlő. Mivel 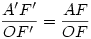 , ebből következik (OF'=1), hogy , ebből következik (OF'=1), hogy  . .
Mivel n>2 egész szám ezért, az AOF szög kisebb mint derékszög. Ezért már csak azt kell bebizonyítani, hogy AF' ív kisebb mint A'F'. Mivel AOF' körcikk benne van az A'OF' háromszögben, ezért a területe is kisebb. A körcikk területe 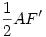 (az AF' ívmérték), a háromszögé pedig (az AF' ívmérték), a háromszögé pedig 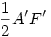 , azaz igaz az A'F' > AF' egyenlőtlenség. Mivel az átalakítások ekvivalensek voltak ezért igaz a kiinduló egyenlőtlenség is. , azaz igaz az A'F' > AF' egyenlőtlenség. Mivel az átalakítások ekvivalensek voltak ezért igaz a kiinduló egyenlőtlenség is.
|
 |
| Előzmény: [349] nadorp, 2006-02-06 17:30:46 |
|
| [359] BohnerGéza | 2006-02-16 00:11:44 |
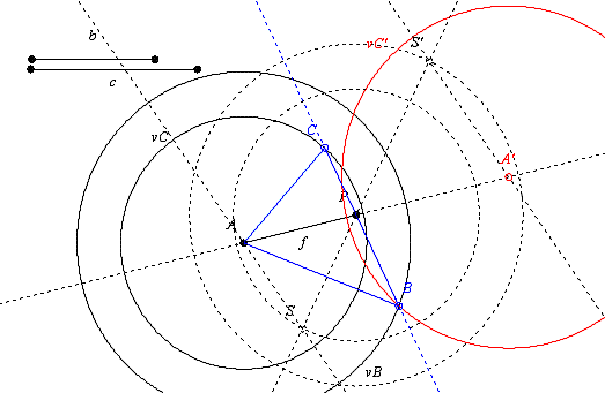
 A 64. feladat megoldásához: Vegyük fel például az AP=f szakaszt, az A kp-ú c sugarú kör vonal a B pont számára ( vB ) és a b sugarú pedig a C számára ( vC ). A szögfelező tételtből tudjuk: ha a vC-re alkalmazzuk a P kp-ú lambda = -c/b arányú hasonlóságot, B számára kapunk egy második vonalat (vC'). ( A szerkesztéshez fölhasználunk egy P-től b-re lévő S segédpontot és képét ( S') P-től c-re, SPS' sorrendben. A vC' A' kp-ú c sugarú kör lesz. )
Megjegyzés: Például az AB szakaszból kiindulva B kp-ú lambda=(b+c)/c hasonlósággal is megoldható a feladat P képe lesz C.
|
 |
|
| [357] Hajba Károly | 2006-02-12 18:58:52 |
 Részemről jöhet az arányos szerkesztés nélküli megoldás. Talán a szögfelezők "tétele" C2 pontjának megszerkesztése a megolodás, de arra még nem jöttem rá, hogy tudom az ismert adatokból megszerkeszteni.
|
| Előzmény: [354] lorantfy, 2006-02-11 20:51:42 |
|
|
| [355] HoA | 2006-02-11 20:56:28 |
 Kedves László!
Megoldásod szép és egyszerű. Két megjegyzés:
- az utolsó előtti sorban "A c oldalt felosztjuk a:c arányban" helyett "A c oldalt felosztjuk b:c arányban" a helyes, és így az ábra legalsó "a" betűje helyett is "b" a jó.
- Az AQP  egyenlőszárú volta "ránézésre" is következik abból, hogy két szöge egyenlő, mert f szögfelező , PAC és APQ váltószögek egyenlőszárú volta "ránézésre" is következik abból, hogy két szöge egyenlő, mert f szögfelező , PAC és APQ váltószögek
|
| Előzmény: [352] lorantfy, 2006-02-11 13:12:31 |
|
|
| [353] Hajba Károly | 2006-02-11 19:49:37 |
 Kedves László!
Az arányosításnál egy kis magyarázatbeli bakit elkövettem, de a szerkesstés menete szabályos. Felszerkesztettem a Te ábrád szerint újra:
t illeszkedik B-re és merőleges f-re. P tükörképe t-re P'. Így az ACP ill. ABP' ill. ABP' hasonlók. AP' hasonlók. AP' f.'. f.'.
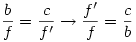 . .
S a szerkesztés menete:
Felveszem az f egyenest és felmérem rá AP szakaszt. Elkészítem a 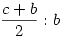 arányosítást f-re. Ez P". Erre a pontra merőlegesen felszerkesztem a t egyenest, majd A-ból rámérem c-t, ez adja a B pontot. Innen már megegyezik a tieddel és nyilvánvaló. arányosítást f-re. Ez P". Erre a pontra merőlegesen felszerkesztem a t egyenest, majd A-ból rámérem c-t, ez adja a B pontot. Innen már megegyezik a tieddel és nyilvánvaló.
|
 |
| Előzmény: [352] lorantfy, 2006-02-11 13:12:31 |
|
| [352] lorantfy | 2006-02-11 13:12:31 |
 Kedves Károly!
Lehet, hogy jó a megoldásod, de én nem értem a magyarázatot. Fölteszem az enyémet, ez is arányos szerkesztéssel megy.
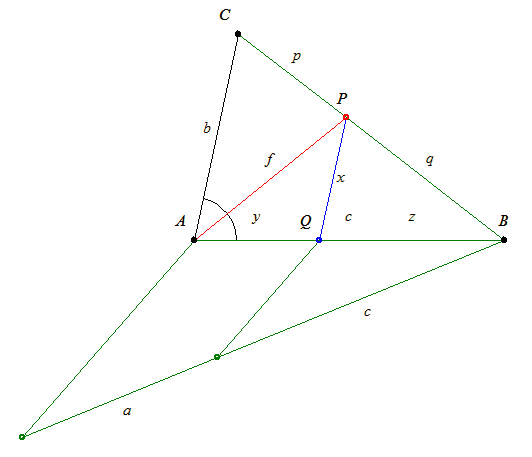
64. feladat megoldása: Adott az ABC háromszögben a b, c oldal és az f szögfelező. A szögfelező a BC oldalt P pontban metszi. Legyen CP=p és PB=q. A szögfelező tételből következik, hogy 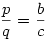 . .
Húzzunk párhuzamost a P pontból AC-vel, ez az AB oldalt Q pontban metszi. Legyen PQ=x, AQ=y és QB=z.
Ekkor a párhuzamos szelők tételéből: 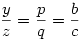 . Vagyis . Vagyis 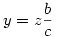
Másrészt a közbenső szakaszokra, QBP és ABC háromszögek hasonlóságából: 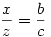 . Vagyis . Vagyis 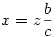
Tehát x=y. Az AQP  egyenlő szárú. A szerkesztés innen már egyszerű. A c oldalt felosztjuk a:c arányban. Q pontból AQ-val, A-ból f-el körözve kapjuk a P pontot. Majd A-ból b-vel körözve BP egyenesből kimetsszük C-t. egyenlő szárú. A szerkesztés innen már egyszerű. A c oldalt felosztjuk a:c arányban. Q pontból AQ-val, A-ból f-el körözve kapjuk a P pontot. Majd A-ból b-vel körözve BP egyenesből kimetsszük C-t.
|
 |
| Előzmény: [351] Hajba Károly, 2006-02-07 13:12:51 |
|
|
| [350] nadorp | 2006-02-06 17:32:00 |
 Természetesen 65. feladat
|
|
| [349] nadorp | 2006-02-06 17:30:46 |
 64.feladat. Egy szabályos n-szög területe T, kerülete K. Bizonyítsuk be szögfüggvények nélkül, hogy 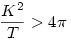
|
|
|
|
| [346] lorantfy | 2006-02-05 13:46:45 |
 64. feladat: Szerkesszünk háromszöget, ha adott az egyik csúcsából induló két oldal és a szögfelező hossza ( a szögfelező egyenesének a háromszögbe eső szakasza)!
|
|
| [345] Karácsony | 2006-01-18 10:05:49 |
 köszönöm!!! a dolgozat egész jól sikerűlt, és sikerűlt elkapnom a fonalat!! egyébként nincs bajom a matekkal, de a legegyszerűbb dolgok szoktak a legtöbb fejtörést okozni. örülök, hogy vannak még ilyen rendes fiúk, akik segítenek a bajbajutottakon!! mégegyszer köszi: Dorka
|
| Előzmény: [344] Sirpi, 2006-01-17 14:26:59 |
|
| [344] Sirpi | 2006-01-17 14:26:59 |
 A 2x-3y=7 attól egy egyenes egyenlete, hogy azok az (x;y) párok, melyekre teljesül ez az egyenlet, éppen egy egyenesen vannak. És ha erről az egyenesről kellenek pontok, könnyen tudunk generálni akárhányat. Pl. ha x=2, akkor ezt az egyenletbe beírva 4-3y=7, ahonnan y=-1, vagyis rögtön kaptuk, hogy a (2;-1) pont rajta van az egyenesen és ezzel a módszerrel újabb pontok is generálhatók.
***
Másik irány: például az A(1;4) és a B(-3;-2) pontokon áthaladó egyenest keressük.
Ahhoz, hogy egy egyenes átmenjen A-n, y=a(x-1)+4 alakúnak kell lennie valamilyen a paraméterrel, hiszen ekkor A koordinátáit behelyettesítve a bal oldal 4, a jobb pedig a(1-1)+4=4 a értékétől függetlenül. a pedig megkapható abból, hogy az egyenes átmegy B-n: -2=a(-3-1)+4, azaz -6=(-4)a, vagyis a=3/2, így az egyenes egyenlete: y=3/2(x-1)+4. Kettővel szorozva: 2y=3x-3+8, ezt pedig rendezve kapjuk, hogy 3x-2y=-5, könnyen utána lehet számolni. Remélem, ez segített valamennyit.
|
| Előzmény: [343] Karácsony, 2006-01-17 13:33:38 |
|
| [343] Karácsony | 2006-01-17 13:33:38 |
 előszőr is köszönöm és hálám örökké üldözni fog. igazából az a baj, hogy elég rossz matektanárunk van és mindig már az elején elvesztem a fonalat! a kérdés az, hogy: 2x-3y=7 egyenesnek adjam meg a két különböző pontját és számítsam ki ezek pontok távolságát. a távolságot már ki tudom számolni, de a pontokig nem jutok el. és azt sem tudom, hogyha két pont koordinátája van meg, akkor abból hogy lesy egzenlet!!
|
| Előzmény: [342] Sirpi, 2006-01-17 13:03:30 |
|
| [342] Sirpi | 2006-01-17 13:03:30 |
 Egy vektor hossza a koordinátái négyzetösszegének négyzetgyöke, azaz:
a(-2;7), b(10;2) esetén a-b=(-2-10;7-2)=(-12;5)
Ennek hossza 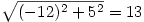
c(3;1) esetén 3c=(9;3)
Ennek hossza: 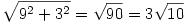 , nem meglepő módon épp háromszor akkora, mint c hossza. , nem meglepő módon épp háromszor akkora, mint c hossza.
***
Az egyenes egyenleténél pedig hogy érted, hogy hogy lesz? Pl. 2 ponton át akarsz egyenest húzni, és annak érdekel az egyenlete? Vagy egy ponton át adott vektorral párhuzamos egyenes egyenlete érdekel? Csak mert ezeket mind meg lehet mondani, a fő kérdés az, hogy Téged mi érdekel pontosan.
|
| Előzmény: [341] Karácsony, 2006-01-17 12:17:57 |
|
| [341] Karácsony | 2006-01-17 12:17:57 |
 KOOrdináta geometria a halálom! szeretnék még segítséget!!! a vektor(-2;7) b vektor (10;2) a kérdés a-b vektor hossza???
a másik: a vektor (3;1) kérdés 3a vektor hossza???
ja és még azt nem értem, hogy hogy lesz az egyenes egyenlete!!!
köszike: Dorka ui: bocsika, de meg fogok bukni, mert csak ebből irat a tanár!!
|
|
|
| [339] Sirpi | 2006-01-17 10:28:48 |
 Fogd fel úgy, mint kétismeretlenes lineáris egyenletrendszert. Törttelenítve:
e: 3x-2y=12
f: 3x-y=6
Másodikból kivonva az elsőt kapjuk, hogy y=-6, ezt pedig bármelyikbe behelyettesítve kijön, hogy x=0.
Tehát a metszéspont a (0;-6) pont.
|
| Előzmény: [338] Karácsony, 2006-01-17 09:44:29 |
|
| [338] Karácsony | 2006-01-17 09:44:29 |
 lenne egy kérdésem, remélem tudtok segíteni. a feladat úgy szól, hogy meg kell határoznbom az e és f egyenesek metszéspontját, ha e: 0,5x-(1/3)y=2 f: 3x-y=6 előre is köszönöm
|
|
|
| [336] philip | 2006-01-11 18:43:04 |
 Nagyon megköszönném,ha valaki tudna nekem segíteni Menelaosz-tételének és annak megfordításának bizonyításában.Vagy az érintő négyszögekre vonatkozó Newton-tétel bizonyításában.
|
|
|
|
| [333] jonas | 2006-01-08 12:08:01 |
 Igen, valóban kell egy abszolútérték bele.
Ha ez az egyenleted van, hogy
(x-u)2=r2-(y-v)2
akkor ebből így vonunk gyököt:
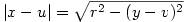
vagy kényelmesebben
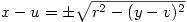
amiből
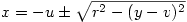
|
| Előzmény: [331] Chryst, 2006-01-08 10:59:05 |
|
| [332] Chryst | 2006-01-08 11:12:05 |
 Az a "-" a gyök előtt az ám "+" akar lenni, csak szerintem mellényúltam és nem vettem észre. Szóval így:
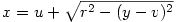
Viszotn most valami nagyon elgondolkodtatott: Ha gyököt vontam, akkor oda nem kellene valahova egy abszolútérték?
Lehet, hogy hülyeség, de suliban is mindig elfelejtkeztem hasonló esetekben az abszolútértékekről, most meg (már) nem tudom, hogy kell-e vagy sem.
|
|
