Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

Fórum: Fizikások válaszoljanak

  [1]    [2]    [3]    [4]    [5]    [6]    [7]    [8]    [9]    [10]    [11]    [12]    [13]    [14]    [15]    [16]    [17]    [18]    [19]    [20]    [21]    [22]    [23]    [24]    [25]    [26]    [27]    [28]    [29]    [30]    [31]    [32]    [33]    [34]    [35]    [36]    [37]    [38]    [39]    [40]    [41]    [42]    [43]    [44]    [45]    [46]    [47]    [48]    [49]    [50]    [51]    [52]    [53]    [54]    [55]    [56]  

Szeretnél hozzászólni? Jelentkezz be.
[1085] szekibarbi2012-05-28 12:43:52

köszönöm mindenkinek a segítséget, pénteken sikeresen 4-re vizsgáztam fizikából!

Nélkületek nem sikerült volna!

Köszönöm!

[1084] szekibarbi2012-05-21 17:15:57

UTOLSÓ FELADATOM! erre valaki tud választ adni?

Egy 0.46 méter sugarú szolenoidon 5.0 amper erősségű áram folyik. Menetsűrűsége 8510 1/m. Mekkora a mágneses indukcióvektor nagysága (mT-ban) a szolenoid közepétől mért 0.86 méter távolságban? (k'=10-7Tm/A)

[1083] Gézoo2012-05-21 16:11:58

Re=Rb+Rk=57*10-3+2,4=2,457 \Omega

I=U/Re=11,8/2,457=4,803 [A]

P=U*I=R*I*I=2,4*23,069=55,3656 [W]

Előzmény: [1082] szekibarbi, 2012-05-21 15:23:44
[1082] szekibarbi2012-05-21 15:23:44

Egy telep elektromotoros ereje 11.8 volt, belső ellenállása 57 m ohm. Egy 2.4 ohmos terhelő ellenállást kapcsolunk rá.Mekkora teljesítmény jut a terhelő ellenállásra (wattban)?

erre tud valaki vmit?

[1081] szekibarbi2012-05-21 14:30:49

megjöttek a Tanártól a válaszok...

Számítsuk ki a nyugalmi energiáját (joule-ban) egy a fény sebességének 90.6Nyugalmi energia = nyugalmi tömeg x fénysebesség négyzete. Azaz 9,109e-31*(3e8)e2=8.198e-14

Számítsuk ki a nyugalmi energiáját (joule-ban) egy a fény sebességének 95százalékával haladó elektronnak! (elektron tömege 9,109×10-31kg, fénysebesség 3×105 km/s) u.a., mint fentebb

Két 620 m/s sebességgel egymással szemben haladó 10 gramm tömegű puskagolyó ütközik és összeragadnak. Mekkora lesz az ütközés utáni és előtti összes nyugalmi tömeg különbsége (kg-ban)? (c = 3×10e5 km/s)

Lényegében az ütközés előtt mozognak a lövedékek, utána pedig állnak; a relativisztikus energia megmarad: 2m/gyök(1-u2/c2) = 2m(vessző)c2 , ahol m az ütközés előtti nyugalmi tömeg, m' az ütközés utáni. Ebből m(vessző)-m = 1/2 m u2/c2. Megjegyzés: az 1/gyök(1-u2/c2) közelítőleg = 1+1/2 u2/c2.

Azaz 1/2*1e-2*620e2/(3e8)e2 = 2.136e-14

[1080] szekibarbi2012-05-21 14:09:59

Egy telep elektromotoros ereje 11.8 volt, belső ellenállása 57 m ohm. Egy 2.4 ohmos terhelő ellenállást kapcsolunk rá.Mekkora teljesítmény jut a terhelő ellenállásra (wattban)?

[1079] szekibarbi2012-05-21 12:44:01

ugyanez köszönöm

Előzmény: [1078] Gézoo, 2012-05-21 12:42:12
[1078] Gézoo2012-05-21 12:42:12

Ha ugyanez a kapcsolás, akkor elegendő a főáram kiszámítása

Az eredő ellenállást ki kell számolni, abból megkapod a főáramot a kapocsfeszültséggel.

Előzmény: [1077] szekibarbi, 2012-05-21 12:39:17
[1077] szekibarbi2012-05-21 12:39:17

és ha ugyanaz a feladat, mint az előző az a soros és párhuzamos kapcsolású, csak nem R3-é kell, hanem R1-é, ami sorosan van bekötve ugyanígy kell számolni? vagy ott más a módszer?

Előzmény: [1076] szekibarbi, 2012-05-21 12:35:11
[1076] szekibarbi2012-05-21 12:35:11

igen, köszönöm, most vettem észre, ez is jó.

Előzmény: [1075] Gézoo, 2012-05-21 12:27:39
[1075] Gézoo2012-05-21 12:27:39

Az előbbit is nézd meg és gondold át! Hátha így már jó!

Előzmény: [1074] szekibarbi, 2012-05-21 12:22:33
[1074] szekibarbi2012-05-21 12:22:33

ez jó!

ma az első :(

Előzmény: [1073] Gézoo, 2012-05-21 12:15:39
[1073] Gézoo2012-05-21 12:15:39

"15.8 volt elektromotoros erejű, ideális telepet kapcsolunk."

Ez azt jelenti, hogy nincs Rb azaz belső ellenállása ezért nincs U=Rb*I feszültség esés sem.

( Rk pedig a k-azaz külső ellenállások eredője.)

Azaz a kérdésre a válasz:

I=U/R3= 15,8/3,9= 4,0513 [A]

Előzmény: [1071] szekibarbi, 2012-05-21 12:06:46
[1072] Gézoo2012-05-21 12:11:25

Húúú igaz! Köszi, hogy észrevetted!

Akkor csak el lehet rontani!

Na akkor nézzük a jó megoldást.

Az áramkörben folyó I=14,24862994 A áram

R1 és R2 ellenállások soros eredőjén

U=Re*I=5,8*14,24862994=82,64205365 [V]

feszültségesést okoz

azaz R3-ra kapcsolódó feszültség:

U=95-82,64205365= 12,35794635 [V]

Így az R3 ellenálláson folyó áram:

I=U/R3=12,35794635/1,1= 11,23449668 [A]

Előzmény: [1070] Kemény Legény, 2012-05-21 12:03:37
[1071] szekibarbi2012-05-21 12:06:46

Három párhuzamosan kötött ellenállásra 15.8 volt elektromotoros erejű, ideális telepet kapcsolunk. Mekkora az R3 ellenálláson átfolyó áram (amperben)? R1 = 6.5ohm , R2 = 2.7ohm , R3 = 3.9ohm?

azt tudom, hogy 15,8V az üresjárati feszültség. meg a könyv szerint

I=U0/Rk+Rb, ahol Rk a külső, Rb a belső ellenállás... de azok mik lesznek?

[1070] Kemény Legény2012-05-21 12:03:37

"Ezt el sem lehet rontani." Biztos, hogy a feladat kérdésére válaszoltál? Nevezetesen az R3 ellenálláson átfolyó áramot kérdezték.

Előzmény: [1065] Gézoo, 2012-05-21 11:42:44
[1069] szekibarbi2012-05-21 12:02:51

a lelkesedésről ne is beszéljünk...

Előzmény: [1068] Gézoo, 2012-05-21 12:01:45
[1068] Gézoo2012-05-21 12:01:45

:( Sajnálom.

Így eléggé érdekes a tanulás. Még a biztost is elbizonytalaníthatja a kapott hibás válaszok sora.

Előzmény: [1067] szekibarbi, 2012-05-21 11:56:49
[1067] szekibarbi2012-05-21 11:56:49

bár van egy teljesen ugyanolyan, más adatokkal, és azt is hibásnak veszi...

Előzmény: [1066] szekibarbi, 2012-05-21 11:49:58
[1066] szekibarbi2012-05-21 11:49:58

az lehet, de hibásnak jelzi... vagy megint rossz a feladat

Előzmény: [1065] Gézoo, 2012-05-21 11:42:44
[1065] Gézoo2012-05-21 11:42:44

Nem jó?

Oké, lépésenként:

1/Re34=1/R3+1/R4

1/Re34=1/1,1+1/4,1=1,152993348

a reciproka: Re34=1/1,152993348=0,867307692

Re=1,4+4,4+0,867307692=6,667307692 [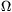\Omega]

I=U/R=95/6,667307692=14,24862994 [A]

Ezt el sem lehet rontani..

Előzmény: [1061] szekibarbi, 2012-05-21 11:06:09
[1064] szekibarbi2012-05-21 11:32:27

nem jó

Előzmény: [1063] Gézoo, 2012-05-21 11:24:50
[1063] Gézoo2012-05-21 11:24:50

Eredmény I=14,24863 [A]

Ugyanis I=U/R=95/6,667307692

Előzmény: [1061] szekibarbi, 2012-05-21 11:06:09
[1062] Gézoo2012-05-21 11:22:04

Barbi!

A megoldás menete R3 és R4 párhuzamos kapcsolás ezért eredőjét kiszámolod:

Re34=1/(1/R3+1/R4)

Majd a sorosokat összeadod

Re=Re34+R1+R2

Előzmény: [1061] szekibarbi, 2012-05-21 11:06:09
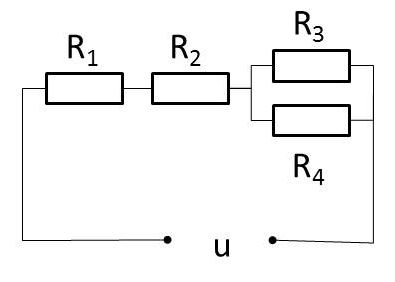
[1061] szekibarbi2012-05-21 11:06:09

Az ábrán látható kapcsolás esetén mekkora áram (amperben) folyik az R3 ellenálláson? R1 = 1.4ohm , R2 = 4.4ohm , R3 = 1.1ohm , R4 = 4.1 ohm, u = 95 V

erre valakinek van ötlete?

nekem kb 84 jött ki, de azt hibásnak írta

  [1]    [2]    [3]    [4]    [5]    [6]    [7]    [8]    [9]    [10]    [11]    [12]    [13]    [14]    [15]    [16]    [17]    [18]    [19]    [20]    [21]    [22]    [23]    [24]    [25]    [26]    [27]    [28]    [29]    [30]    [31]    [32]    [33]    [34]    [35]    [36]    [37]    [38]    [39]    [40]    [41]    [42]    [43]    [44]    [45]    [46]    [47]    [48]    [49]    [50]    [51]    [52]    [53]    [54]    [55]    [56]