| [685] Fálesz Mihály | 2012-04-18 16:33:55 |
 Amikor a fénysebességet 3.108 m/s-re kerekítjük, tudhatjuk, hogy a végeredményből legfeljebb csak 3-4 jegy lesz pontos.
(A számolás közben nem teljesen értelmetlen sok jegyig számolni, ha ennyire közeli számok különbsége a kérdés.)
|
| Előzmény: [684] Gézoo, 2012-04-17 07:57:56 |
|
| [684] Gézoo | 2012-04-17 07:57:56 |
 Egyszerű az ok, a kalkulátorból másoltam az eredményt, és így Barbi annyi jegyet használhatott fel amennyit jónak látott. (A feladat kiírást csak az ideírt mélységig ismerhettem, ezért nem tudom, hogy milyen formátumban kell továbbküldeni.)
|
| Előzmény: [683] Róbert Gida, 2012-04-16 14:35:23 |
|
|
| [682] Róbert Gida | 2012-04-16 14:31:35 |
 "mindegy, valszeg ez is hibásan van kiírva, normál alak ugyanis nem megengedett :D"
Amit Gézoo írt delta m-re az éppen nem normálalakban volt. Majd alkalomadtán nézz utána, hogy mi a normálalak. (normálalak és nem normál alak).
|
| Előzmény: [681] szekibarbi, 2012-04-16 13:52:53 |
|
|
| [680] Gézoo | 2012-04-16 13:51:46 |
 Jajj bocs.. a NÖVEKEDÉS..
Azaz m-m0=21,970136932028895713151119283013e-31 - 9,109e-31 =
delta m=12,86113693202889571315111928301e-31 [kg]
ennyivel növekedett a tömeg..
|
| Előzmény: [679] Gézoo, 2012-04-16 13:38:13 |
|
| [679] Gézoo | 2012-04-16 13:38:13 |
 Az elv jó m=m0*ß ahol ß =1/gyök(1-(0,91/1)2) Csak a számértékkel nekem más jön ki..
ß=2,411915350974738798238129243936 (gyökös)
ß=2,411915350974738798238129243936 (szögfüggvényes)
m=9,109e-31*2,411915350974738798238129243936=
m=2,1970136932028895713151119283013e-30 [kg]
Vagy csak rosszul látom?
|
| Előzmény: [678] szekibarbi, 2012-04-16 13:15:20 |
|
| [678] szekibarbi | 2012-04-16 13:15:20 |
 lemaradt a példa eleje :D
Számítsuk ki a tömegnövekedését (kg-ban) egy a fény sebességének 91.0 százalékával haladó elektronnak! (elektron tömege 9,109×10-31kg, fénysebesség 3×105 km/s)
|
| Előzmény: [677] szekibarbi, 2012-04-16 13:12:22 |
|
| [677] szekibarbi | 2012-04-16 13:12:22 |
 Számítsuk ki a tömegnövekedését (kg-ban) egy a fény sebességének 91.0
jól gondolom?
m= m0/gyök1-v2/c2
ami ugyebár 9,109×10-31kg/gyök1-0,91*0,91 ez egyenlő 2,17×10-30kg
jól gondolom?
|
|
| [676] Gézoo | 2012-04-16 12:50:37 |
 Lemaradt a végéről, ( a linken van, de itt nem látszik,) hogy ha valakinek bármi ellenvetése, kérdése, véleménye van, nyugodtan írja le.
|
| Előzmény: [675] Gézoo, 2012-04-16 12:26:48 |
|
| [675] Gézoo | 2012-04-16 12:26:48 |
 A fizika akkor a legérthetőbb ha eljátsszuk a folyamatokat.
Két részecske közötti hatás-ellenhatás létrejöttének a szimulálását végezzük el egy játékkal:
Modellezzük a részecskék közötti kölcsönhatásokat, amit a fotonok okoznak.
Jégpályán tegyünk a jégre egymás mellé két műanyag bobot és beléjük egy-egy gyereket akik egymásnak medicinlabdát dobálnak. A labda szimbolizálja a fotont és a bobos gyerekek a részecskéket.
A bobok eltávolodnak egymástól. Az időegységre eső eltávolodás függ a köztük lévő távolságtól, hiszen a labdának a sebessége közel állandó, de a távolság növekedésével egyre hosszabb utat kell befutnia.
Azaz a dobások időegységre jutó száma a távolsággal csökken. ezzel az átadott lendületek száma is csökken.
Ha pedig az egyik bobot a másik felé toljuk, "kényszerítjük", akkor ezzel a dobálás hatásaként a másik bobot is eltoljuk, mintha rugó lenne a két bob között.
A játék kedvéért próbáljuk meg az egyik bob mozgatásával körbetolni a pályán a másik bobot!
Közben érezni fogjuk a labda eldobásakor és a visszaérkezésekor fellépő impulzusokat, azaz az ellenhatás felét eldobáskor és másik felét a labda visszaérkezésekor, mint ahogyan itt leírtam.
Sőt! Ha a tolás-kényszerítés időegységre eső sebesség változását változtatjuk, akkor a labda lendületével tolt másik bob gyorsulása is változni fog.
Persze ehhez az időegységre eső dobások száma is növekedni fog. Mégpedig a gyorsulás mértékével egyenesen arányos módon.
Mint az "életben" amikor egyik test gyorsulásra kényszerít egy másik testet.
|
|
| [674] Gézoo | 2012-04-16 12:08:50 |
 Először is bocs, hogy az előbb a nevedbe belekerült egy "r"..
A felvetésedre pedig, igen. Természetesen a végeredményt transzformálva nem kaphatunk mást. Csupán azért merült fel bennem ez a lehetőség, mert nem tudhattam, hogy a feladatot kiíró kolléga esetleg nem azt fogalmazta-e meg, mint amilyen választ várt, hanem a másik oldalról értelmezte a feladatot.
|
| Előzmény: [673] Geg, 2012-04-16 12:04:14 |
|
| [673] Geg | 2012-04-16 12:04:14 |
 Nincs elteres, ez ugyanaz. Irj be x helyere vt -t (hiszen a nyugvo rendszerbol nezve pont ekkora a megtett tavolsag), es megkapod a szokasos kepletet.
|
| Előzmény: [668] Gézoo, 2012-04-16 11:19:38 |
|
|
|
| [670] Gézoo | 2012-04-16 11:36:25 |
 :D Részemről: Szívesen..
Nagy tanulságul szolgáljon emlékeidben a tegnapi nap.
Eszembe jut róla a fagyban didergő kis veréb.. Amikor rápottyant egy lepényt az arra járó tehén, majd jön egy macska, kihúzza a lepényből, megtisztogatja és felfalja.
Tanulság?
Akiről azt hinnéd, hogy magasról tesz a fejedre arról ha jobban meggondolod belátod, hogy sokkal többet segített, mint az aki kihúzott a lepényből..
|
| Előzmény: [669] szekibarbi, 2012-04-16 11:30:47 |
|
| [669] szekibarbi | 2012-04-16 11:30:47 |
 megelégeltem, és írtam a tanárnak! a válasz:
Kedves Barbara!
A megoldása jó, a feladatkiírásban szerepelt rosszul a kérdés. Ugyanis nem s-ben hanem ps-ben kell beírni a végeredményt. Köszönöm, hogy szólt. Javítottam a feladatot a moodle-ben is.
Üdvözlettel: Erdélyi Zoltán
ezúton is mindenkinek köszönöm a segítséget
|
| Előzmény: [668] Gézoo, 2012-04-16 11:19:38 |
|
| [668] Gézoo | 2012-04-16 11:19:38 |
 Nagy Sándor megoldása itt is jól jöhet..
Esetleg lehet egy pici elvi eltérés az általunk (Alma, Greg, és én általam) írt válasz és az elvárt válasz között.
Ugyanis a relatív idő függvénye szerint 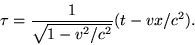
A beérkezés időpontjából számolt kezdő időpont a főnök rendszerében máskor van mint az autó rendszerében. És ugye tanultátok, hogy az időpontok közötti távolsággal számolunk. azaz
t=1,0000000000000037555555555555767*(5*3600-12168000/9e16) t=1,0000000000000037555555555555767*17999,9999999998648 t=17999,99999999993239999999999986 [sec]
Így a delta
t=6,7600000000000139751111111115375e-11 [sec]
Csak az a kérdés, hogy milyen mélységgel számoltok a gyakorlatokon.
|
| Előzmény: [666] szekibarbi, 2012-04-16 11:01:25 |
|
|
| [666] szekibarbi | 2012-04-16 11:01:25 |
 nincs megadva, vizsgán is ezt a felületet használjuk, így feltételezem sima egyszerű (illetve tudományos) számológép használatával kell az eredményt kiszámolni. normál alakban nem adható meg az eredmény, a beadandó tizedesek száma sincs meghatározva, őszintén ez egy elég nagy hibája az oldalnak, van ahol 2 is elég a helyes megoldás eléréséhez, van ahol 3-4 is kell (ez sajnos nincs jelölve) remélem, a vizsgán meg lesz adva. portál használatához nem találok kiírást.
a legnagyobb Gordiuszi csomó
|
| Előzmény: [663] Gézoo, 2012-04-16 10:58:14 |
|
|
|
| [663] Gézoo | 2012-04-16 10:58:14 |
 A hibát nem csak a számjegyek száma, hanem a használt számológép pontossága is okozhatja.
Nincs előírva az, hogy milyen eszközzel számolj? Vagy a beadandó tizedesek száma? Esetleg a normál alak jelölésének módja?
Karakteres vagy numerikus a bemeneti pont?
Nincs valami leírásod a portál használatához?
|
| Előzmény: [658] szekibarbi, 2012-04-16 10:50:59 |
|
|
|