KöMaL Problems in Mathematics, December 2018
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on January 10, 2019. |
K. 604. Find five appropriate distinct positive integers such that the sums of every possible selection of numbers out of those five is different. Find a set of five such numbers in which the largest number is as small as possible.
(6 pont)
solution (in Hungarian), statistics
K. 605. Define a cup as a figure formed by three small cubes pairwise sharing an edge in common (see the figure). We are building rectangular blocks out of small unit cubes.
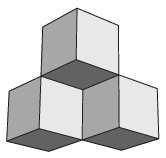
\(\displaystyle a)\) How many cups are there in a \(\displaystyle 4\times4\times2\) block?
\(\displaystyle b)\) How many cups are there in a \(\displaystyle 4\times4\times3\) block?
(6 pont)
solution (in Hungarian), statistics
K. 606. The length of sides \(\displaystyle AB\), \(\displaystyle BC\), \(\displaystyle CD\) and \(\displaystyle DE\) of a pentagon \(\displaystyle ABCDE\) is unity, \(\displaystyle \angle ABC\) and \(\displaystyle \angle CDE\) are both \(\displaystyle 90^{\circ}\). Show that the plane can be tiled with such pentagons without gaps or overlaps. Show it for both convex and concave pentagons.
(6 pont)
solution (in Hungarian), statistics
K. 607. Regular hexagons are constructed out of congruent regular triangles as shown in the figure. The first one consists of six triangles, the second one consists of twenty-four.

\(\displaystyle a)\) How many triangles does the sixth such hexagon consist of?
\(\displaystyle b)\) We have 2017 such regular triangles. If we use them to construct the largest possible hexagon of this kind, how many triangles are left over?
(6 pont)
solution (in Hungarian), statistics
K. 608. \(\displaystyle a)\) Show that there are infinitely many integers whose squares end in three digits of 4.
\(\displaystyle b)\) Is there a positive integer whose square ends in four digits of 4?
(6 pont)
 |
Problems with sign 'C'Deadline expired on January 10, 2019. |
C. 1511. \(\displaystyle B\) and \(\displaystyle C\) are interior points of a line segment \(\displaystyle AD\) such that \(\displaystyle AB=CD\). Prove that \(\displaystyle PA+PD\ge PB+PC\) for any point \(\displaystyle P\) of the plane.
(5 pont)
solution (in Hungarian), statistics
C. 1512. We are making 50-gram cubes out of three different mixtures of red, white and green play dough. In the first type of cube, the proportion of the colours is \(\displaystyle 3:2:0\), in the second type it is \(\displaystyle 1:3:1\), and in the third type it is \(\displaystyle 0:1:4\). How many of each type should we make if we want to use \(\displaystyle 1\) kg of each colour altogether?
(5 pont)
solution (in Hungarian), statistics
C. 1513. Show that every perfect cube can be expressed as a difference of two perfect squares.
(5 pont)
solution (in Hungarian), statistics
C. 1514. A unit square is divided into four isosceles triangles by connecting an interior point to the vertices. Find the minimum and maximum values of the product of the areas of the four triangles.
(5 pont)
solution (in Hungarian), statistics
C. 1515. Find the real solutions of the equation where \(\displaystyle k\) is an odd positive integer:
\(\displaystyle \big(1-x+x^2\big) \big(1-x+x^2-\ldots +x^{2k}\big)= \big(1-x+x^2-\ldots +x^{k+1}\big)^2. \)
(5 pont)
solution (in Hungarian), statistics
C. 1516. From point \(\displaystyle P(16,7)\) of the coordinate plane, a tangent is drawn to the circle of radius \(\displaystyle r=5\sqrt{3}\) centred at \(\displaystyle O(4,-2)\). Let \(\displaystyle P'\) denote the orthogonal projection of the point of tangency onto the line segment \(\displaystyle OP\). Find the coordinates of \(\displaystyle P'\).
(5 pont)
solution (in Hungarian), statistics
C. 1517. The fields of a chessboard are coloured in three colours as shown in the figure. A knight is placed on a random field of the chessboard, and a random (but correct) move is made with that knight. What is the probability that the knight will arrive on a field that has the same colour as the starting field?
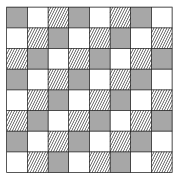
(5 pont)
 |
Problems with sign 'B'Deadline expired on January 10, 2019. |
B. 4990. Let \(\displaystyle n\) denote a natural number greater than one. Let \(\displaystyle d(n)\) denote the number of positive divisors of \(\displaystyle n\), and let the sum of the divisors be \(\displaystyle \sigma(n)\). Show that \(\displaystyle \sigma(n) > d(n)\sqrt n\,\).
Proposed by Zs. Sárosdi, Veresegyház
(3 pont)
solution (in Hungarian), statistics
B. 4991. Arthur and Belle take turns in colouring the edges of a cube red. In each step, they colour an edge that is skew to the previously coloured edge. Artur starts. The player who cannot do an appropriate coluring will lose the game. Which player has a winning strategy?
(3 pont)
solution (in Hungarian), statistics
B. 4992. To start, each of the numbers \(\displaystyle 1,2,\ldots, n\) is coloured either red or blue. In every move, three distinct numbers in arithmetic progression are selected, and the colour of each of the three numbers is changed. For what values of \(\displaystyle n\) is it true that however the numbers \(\displaystyle 1,2,\ldots, n\) are coloured initially, it is possible to turn all of them red by applying an appropriate sequence of such steps?
Proposed by S. Róka, Nyíregyháza
(4 pont)
solution (in Hungarian), statistics
B. 4993. A square is drawn over each of legs \(\displaystyle BC\) and \(\displaystyle CA\) of a right-angled triangle \(\displaystyle ABC\). Let \(\displaystyle D\) and \(\displaystyle E\) denote the vertices of the squares that lie opposite to \(\displaystyle C\). Show that the circumscribed circle of triangle \(\displaystyle ABC\) passes through the midpoint of line segment \(\displaystyle DE\).
(4 pont)
solution (in Hungarian), statistics
B. 4994. Prove that if the cubic equation \(\displaystyle x^3+Ax^2+Bx+C=0\) has three distinct positive roots for some values of the real parameters \(\displaystyle A\), \(\displaystyle B\) and \(\displaystyle C\), then \(\displaystyle A^2+B^2+18C>0\).
(German problem)
(4 pont)
solution (in Hungarian), statistics
B. 4995. Let \(\displaystyle D\), \(\displaystyle E\) and \(\displaystyle F\), respectively, denote the midpoints of sides \(\displaystyle BC\), \(\displaystyle CA\) and \(\displaystyle AB\) of a right-angled but not isosceles triangle \(\displaystyle ABC\), let \(\displaystyle O\) be the centre of the circumscribed circle of the triangle, and let \(\displaystyle M\) be the orthocentre. The tangent drawn to the circumscribed circle at \(\displaystyle A\) intersects line \(\displaystyle EF\) at \(\displaystyle P\), and the tangent drawn at point \(\displaystyle B\) intersects line \(\displaystyle FD\) at \(\displaystyle Q\). Show that lines \(\displaystyle PQ\) and \(\displaystyle OM\) are perpendicular.
Proposed by B. Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
B. 4996. Given a line segment and one point that divides it \(\displaystyle 1:2\), construct the other point dividing the line segment \(\displaystyle 1:2\) by only using a straight edge.
(6 pont)
solution (in Hungarian), statistics
B. 4997. Consider the following sequence \(\displaystyle p_n(x)\) of polynomials with integer coefficients: let \(\displaystyle p_0(x)=0\), \(\displaystyle p_1(x)=1\), and for all \(\displaystyle n\ge 2\) let
\(\displaystyle p_n(x)=p_{n-1}(x)+x\cdot p_{n-2}(x). \)
Prove that if a polynomial \(\displaystyle f(x)\) divides the polynomials \(\displaystyle p_n(x)\) and \(\displaystyle p_m(x)\) for some positive integers \(\displaystyle n\), \(\displaystyle m\) then it also divides the polynomial \(\displaystyle p_{(m,n)}(x)\).
(\(\displaystyle (n,m)\) denotes the greatest common divisor of \(\displaystyle n\) and \(\displaystyle m\). A polynomial \(\displaystyle P(x)\) divides a polynomial \(\displaystyle Q(x)\) if there exists a polynomial \(\displaystyle R(x)\) of real coefficients for which \(\displaystyle Q(x)=P(x)R(x)\).)
(6 pont)
 |
Problems with sign 'A'Deadline expired on January 10, 2019. |
A. 737. \(\displaystyle 100\) points are given in space such that no four of them lie in the same plane. Consider those convex polyhedra with five vertices that have all vertices from the given set. Prove that the number of such polyhedra is even.
Proposed by: Gyula Károlyi, Budajenő
(7 pont)
A. 738. (Our original problem in December was wrong. Here we post a new one. You can submit it together with the three problems in January.)
Consider the following sequence: \(\displaystyle a_1=1\), \(\displaystyle a_2=2\), \(\displaystyle a_3=3\), and
\(\displaystyle a_{n+3}=\frac{a_{n+1}^2+a_{n+2}^2-2}{a_n}\)
for all integers \(\displaystyle n\ge 1\). Prove that every term of the sequence is a positive integer.
(7 pont)
solution (in Hungarian), statistics
A. 739. Let \(\displaystyle a_1,a_2,\ldots\) be a sequence of real numbers from the interval \(\displaystyle [0,1]\). Prove that there is a sequence \(\displaystyle 1\le n_1<n_2<\ldots\) of positive integers such that
\(\displaystyle A=\lim_{\substack{i, j\to \infty\\i\ne j}} a_{n_i+n_j} \)
exists, i.e., for every real number \(\displaystyle \varepsilon>0\) there is a \(\displaystyle N_\varepsilon\) such that \(\displaystyle \big|a_{n_i+n_j}-A\big| < \varepsilon\) is satisfied for any pair of distinct indices \(\displaystyle i,j>N_\varepsilon\).
CIIM 10, Colombia
(7 pont)
Upload your solutions above.
