KöMaL Problems in Mathematics, March 2023
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on April 11, 2023. |
K. 759. Each member of a group of nine people knows exactly four others. (Acquaintances are mutual.)
\(\displaystyle a)\) Is it possible that every pair of people have an acquaintance in common?
\(\displaystyle b)\) Is it true that any pair of people either know each other directly or have an acquaintance in common?
(5 pont)
solution (in Hungarian), statistics
K. 760. Triangle \(\displaystyle A(2;4)\), \(\displaystyle B(6;4)\), \(\displaystyle C(4;10)\) is reflected (in succession) in the line \(\displaystyle x = a\), and then in the line \(\displaystyle y = 2\).
\(\displaystyle a)\) What is the sum of the second coordinates of the vertices obtained by the second reflection?
\(\displaystyle b)\) What is the value of \(\displaystyle a\) if the sum of the first coordinates of the vertices obtained by the second reflection is 36?
(5 pont)
solution (in Hungarian), statistics
K. 761. John is making new fractions out of the fraction 3/5 by writing the same digit in both the numerator and the denominator—either in front of or behind the existing digit—to obtain two-digit numbers. What is the largest difference between the numbers that can be formed in this way?
(5 pont)
 |
Problems with sign 'K/C'Deadline expired on April 11, 2023. |
K/C. 762. Each field of a \(\displaystyle 5\times5\) table is selected in some order, and a number is written in it. The number written in a particular field is the number of fields sharing a common edge with this field and already containing some numbers.
(For example, the fields of the table may have been filled in in the following order: a5, b5, c5, d5, e5, e4, e3, e2, a4, a3, a2, a1, b1, c1, d1, e1, \(\displaystyle \ldots\,\).)
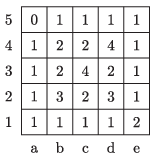
Fill in the table in two other possible ways. Add the numbers in all the fields.
Prove that the sum of the numbers will always be 40, no matter how the table is filled in according to the rule.
(5 pont)
solution (in Hungarian), statistics
K/C. 763. Two squares are drawn in a semicircle of unit radius such that they both lie along the diameter, they have another side along a common line, and each has a vertex on the arc of the semicircle (see the figure).

Given that the radii drawn from the centre of the circle to the vertices lying on the circular arc are perpendicular, prove that the sum of the areas of two squares drawn in this way is constant.
(5 pont)
 |
Problems with sign 'C'Deadline expired on April 11, 2023. |
C. 1758. Adam found a magic square in a magazine. (A magic square is a \(\displaystyle 3\times3\) table of numbers in which the sum of the numbers is the same in all rows, columns and diagonals, see the figure.) He filled in the square correctly, and then selected a row or column at random. He wrote down the three numbers in the order as they appeared left to right or top down. These are the numbers \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) in the equation \(\displaystyle ax^2 + bx + c = 0\). Adam was happy to observe that the resulting equation had two distinct real roots, and calculated the sum of the squares of the roots. What numbers may he have got as a result?
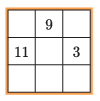
Proposed by O. Teleki, Tököl
(5 pont)
solution (in Hungarian), statistics
C. 1759. Two right-angled triangles \(\displaystyle ABC\) and \(\displaystyle EDC\) are drawn next to each other, as shown in the figure.
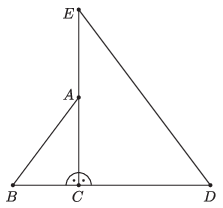
In triangle \(\displaystyle ABC\), \(\displaystyle BC=3\), \(\displaystyle CA=4\), and in triangle \(\displaystyle EDC\), \(\displaystyle DC=6\), \(\displaystyle CE=8\). The circumscribed circle of triangle \(\displaystyle ABE\) intersects line \(\displaystyle DE\) again at \(\displaystyle P\), and line \(\displaystyle DB\) at \(\displaystyle Q\). Find the exact value of the ratio of the area of quadrilateral \(\displaystyle ABDE\) to the area of pentagon \(\displaystyle AEPQB\).
Proposed by B. Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
C. 1760. Find all positive integers for which the sum of the number and its factorial equals the cube of the number.
(5 pont)
solution (in Hungarian), statistics
C. 1761. An equilateral triangle is cut with a line parallel to one of the sides. The circumscribed circles of the resulting triangle and trapezium are drawn. Is it possible that the ratio of the circumradius of the trapezium to that of the triangle is \(\displaystyle \frac{\sqrt{3}}{3}\)?
Proposed by Zs.\(\displaystyle \,\)M. Tatár, Esztergom
(5 pont)
solution (in Hungarian), statistics
C. 1762. Is there a positive prime number \(\displaystyle p\) for which
\(\displaystyle \log_{p-2}(4p-11)=m, \)
where the parameter \(\displaystyle m\) denotes one of the digits of \(\displaystyle 2023\)?
Proposed by B. Bíró, Eger
(5 pont)
 |
Problems with sign 'B'Deadline expired on April 11, 2023. |
B. 5302. Either \(\displaystyle +1\) or \(\displaystyle -1\) is written in every field of an \(\displaystyle 8 \times 8\) table so that the sum of all entries is 0. The sum of the numbers is calculated for each row and column. What is the maximum possible number of positive sums out of the 16 sums obtained in this way?
Based on the idea of M.\(\displaystyle \,\)E. Gáspár, Budapest
(3 pont)
solution (in Hungarian), statistics
B. 5303. The isosceles right-angled triangle \(\displaystyle ABC\) has its right angle at \(\displaystyle C\). \(\displaystyle D\) is an interior point of side \(\displaystyle BC\) such that the angle \(\displaystyle CDA\) is \(\displaystyle 75^\circ\). Given that triangle \(\displaystyle ADC\) has unit area, prove that \(\displaystyle BD = 2\).
Proposed by M. Hujter, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 5304. \(\displaystyle a)\) Are there positive integers \(\displaystyle a\) and \(\displaystyle b\) such that
\(\displaystyle a+b \mid a^2+b^2, \quad\text{but}\quad a+b \nmid a^4 + b^4? \)
\(\displaystyle b)\) Are there positive integers \(\displaystyle a\) and \(\displaystyle b\) such that
\(\displaystyle a+b \mid a^4+b^4, \quad\text{but}\quad a+b \nmid a^2+b^2? \)
Proposed by B. Hujter, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 5305. Let \(\displaystyle A_1\) and \(\displaystyle A_2\), respectively, denote the points lying closer to \(\displaystyle B\) and closer to \(\displaystyle C\) that divide side \(\displaystyle BC\) of a triangle \(\displaystyle ABC\) in a 1:2 ratio. Define points \(\displaystyle B_1\) and \(\displaystyle B_2\) on side \(\displaystyle CA\), and points \(\displaystyle C_1\) and \(\displaystyle C_2\) on side \(\displaystyle AB\) in an analogous way. Prove that the centroid of triangle \(\displaystyle ABC\) lies on the line joining the common points of the circumscribed circles of triangles \(\displaystyle A_1B_1C_1\) and \(\displaystyle A_2B_2C_2\).
Proposed by B. Bíró, Eger
(4 pont)
solution (in Hungarian), statistics
B. 5306. We have a weighted (six-sided) die and a weighted coin. On one side of the coin there is one dot, and on the other side there are two dots. The expected value of the number of dots appearing on top is the same for the die and the coin. Show that if the die and the coin are thrown simultaneously then the probability of getting more dots on the coin than on the die is greater than the probability of getting more dots on the die than on the coin.
Proposed by V. Vígh, Sándorfalva
(5 pont)
solution (in Hungarian), statistics
B. 5307. The area of an acute-angled triangle is \(\displaystyle T\), its inradius is \(\displaystyle r\), and its circumradius is \(\displaystyle R\). Show that
\(\displaystyle \sqrt{3}T \le {(r+R)}^2. \)
Proposed by L.\(\displaystyle \,\)B. Simon, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 5308. Let \(\displaystyle a_n\) denote the least common multiple of the positive integers \(\displaystyle n+1,n+2,\ldots,n+10\). Find the greatest real number \(\displaystyle \lambda\) for which \(\displaystyle \lambda a_{n}\le a_{n+1}\) is always true.
Proposed by P.\(\displaystyle \,\)P. Pach, Budapest
(6 pont)
solution (in Hungarian), statistics
B. 5309. Given the axis and two points of a parabola, construct its focus and directrix.
Proposed by G. Holló, Budapest
(6 pont)
 |
Problems with sign 'A'Deadline expired on April 11, 2023. |
A. 848. Let \(\displaystyle G\) be a planar graph, which is also bipartite. Is it always possible to assign a vertex to each face of the graph such that no two faces have the same vertex assigned to them?
Submitted by Dávid Matolcsi, Budapest
(7 pont)
A. 849. For real number \(\displaystyle r\) let \(\displaystyle f(r)\) denote the integer that is the closest to \(\displaystyle r\) (if the fractional part of \(\displaystyle r\) is 1/2, let \(\displaystyle f(r)\) be \(\displaystyle r-1/2\)). Let \(\displaystyle a>b>c\) rational numbers such that for all integers \(\displaystyle n\) the following is true: \(\displaystyle f(na)+f(nb)+f(nc)=n\). What can be the values of \(\displaystyle a\), \(\displaystyle b\) and \(\displaystyle c\)?
Submitted by Gábor Damásdi, Budapest
(7 pont)
A. 850. Prove that there exists a positive real number \(\displaystyle N\) such that for arbitrary real numbers \(\displaystyle a,b>N\) it is possible to cover the perimeter of a rectangle with side lengths \(\displaystyle a\) and \(\displaystyle b\) using non-overlapping unit disks (the unit disks can be tangent to each other).
Submitted by Benedek Váli, Budapest
(7 pont)
Upload your solutions above.
