|
| [719] juantheron | 2012-05-17 08:49:02 |
 Thanks Nadorp got it
task:: find positive Integer value of x and y for which x2+3y and y2+3x is an perfect square
My solution::
Let x2+3y=l2 and y2+3x=m2
Where l,m Z Z
Then (x2-y2)-3(x-y)=l2-m2
(x-y).(x+y-3)=(l+m).(l-m)
means either x+y-3=l+m and x-y=l-m
2x=3+2l or 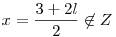
similarly 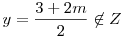
but when i put rendomly put values like (1,1) and (11,16) and (16,11)
but how can i calculate it
Thanks
|
|
|
| [717] juantheron | 2012-05-16 20:17:02 |
 Nwe task::
The number of ordered pairs of positive integers x,y such that x2+3y and y2+3x are both perfect squares
|
|
| [716] juantheron | 2012-05-16 19:46:00 |
 Yes Friends your answer is Right
I have solved like that way
x2=4+[x]
here R.H.S(right hand side) is an Integer that means L.H.S(Left hand side must be an Integer)
So x2 Z Z
So Let x2=k, where k>0
So 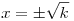
So our equation convert into ![k=4+[\pm \sqrt{k}]](keplet.cgi?k=35D7CCA2B1205F53)
Now after checking certain value of k like k=1,2,3,4,5,6
We Get only k=2 and k=6 satisfy the given equation
and after k 7, we get L.H.S # R.H.S 7, we get L.H.S # R.H.S
But Not sure about k 7 has no value for which satisfy the given equation 7 has no value for which satisfy the given equation
can anyone clear last line explanation
Thanks
|
|
| [715] juantheron | 2012-05-16 19:35:38 |
 Thanks Nadorp and Small Potato
for Integration I have solve it after yours work
I have solved it like in that way
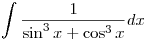
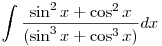
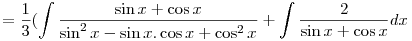
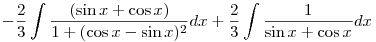
Put (cos x-sin x)=tand (sin x+cos x)dx=-dt
and 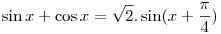
after that we can calculate easily
|
|
|
|
|
|
| [710] nadorp | 2012-05-16 13:00:34 |
 Igazad van, de azért beírom, mert nem nehéz
sin3x+cos3x=(sin x+cos x)(1-sin xcos x)
Végezzük el az integrálban a
cos x-sin x=s helyettesítést
Ekkor 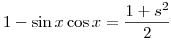 és és
(sin x+cos x)2+(cos x-sin x)2=2 és
-(sin x+cos x)dx=ds miatt
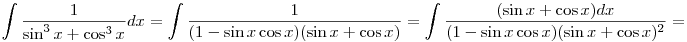
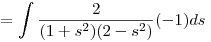
Innen már könnyű...
|
| Előzmény: [709] SmallPotato, 2012-05-16 11:51:16 |
|
|
| [708] logarlécész | 2012-05-16 11:05:44 |
 Ha jól értem, a megoldás kellene.
A legegyszerűbb grafikusan. A felrajzolásból látszik, hogy megoldás lesz a +2; -2 és lesz még egy megoldás -3 és -2 között. Ennek a pontos értékét én sem tudom meghatározni, nagyjából -2,19258, ha nem tévedek.
|
| Előzmény: [707] juantheron, 2012-05-16 10:10:27 |
|
|
|
|
| [704] Lóczi Lajos | 2012-05-15 20:21:56 |
 Fejezzük ki valamelyik változót a másik segítségével az
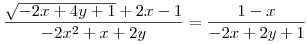
egyenletből.
|
|
|
|
| [701] Kemény Legény | 2011-12-29 01:30:08 |
 Erről a maradékosztályos témáról eszembe jutott egy viszonylag nehéz feladat (nem saját). Azt hiszem, a fórumon még nem szerepelt:
Legyen p>2 prímszám, és tekintsük a
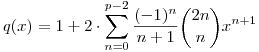
egész együtthatós polinomot. Bizonyítsuk be, hogy q-nak van gyöke modulo p, azaz létezik olyan x egész, hogy q(x) osztható p-vel.
Példa: p=7 esetén a polinom:
q(x)=1+2x-2x2+4x3-10x4+28x5-84x6.
Ennek az értéke pl. x=5 esetén q(5)=-1230789 osztható 7-tel, azaz p=7-re az állítás teljesül.
Továbbá megkönnyítendő az ellenőrzést, elárulom, hogy p=3, 5, 7, 11, 13, 17, 19 esetén az alább x-ek rendre jó választást adnak: x=2, 1, 5, 8, 3, 4, 14.
|
|
| [700] vogel | 2011-12-28 22:36:27 |
 Ha az 1-et tekinti egységnek, akkor 2 inverze 4 mod 7, ha a szorzás a művelet.
|
|
| [699] Kemény Legény | 2011-12-28 22:14:29 |
 Azért az nem kellene elfelejteni, hogy testben lehet osztani 0-tól különböző elemmel, és a 7 szerencsés módon egy prím, ezért a mod 7 maradékosztályok testet alkotnak.
|
| Előzmény: [697] HoA, 2011-12-28 21:31:30 |
|
| [698] Füge | 2011-12-28 21:50:22 |
 Kongruenciát úgy oszthatsz, ha a mod-ot is leosztod a mod és az osztó legnagyobb közös osztójával. Tehát a 2 kongruens 8 (mod 6)-ból következik, hogy 1 kongruens 4 (mod 3).
|
| Előzmény: [697] HoA, 2011-12-28 21:31:30 |
|
| [697] HoA | 2011-12-28 21:31:30 |
 De ezt ugye butaságnak tartjuk? Még egészekre sem igaz ilyesmi. Pl. 2 kongruens 8 ( mod 6 ) -ból nem következik 1 kongruens 4 ( mod 6 )
|
| Előzmény: [695] Hölder, 2011-12-27 00:03:56 |
|
|



 6 and 3
6 and 3 Z
Z  4+x
4+x  7, we get L.H.S # R.H.S
7, we get L.H.S # R.H.S 




