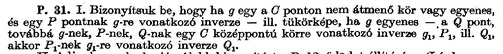| [1148] BD | 2021-10-17 12:55:18 |
 Üdv! Két kérdésem lenne a szeptemberi fizikafeladatok megoldásával kapcsolatban. Egyrészt a P. 5340-ben az ábra szerint végig vöröseltolódik a hullám a 45 perces periódusokban, amikor nem takarja a bolygó. Tehát a hullámforrás végig távolodik tőlünk. De a megoldás szerint körpályán kering a műhold a bolygója körül. Ebben nincs ellentmondás? Mármint akkor egy ideig közelednie kéne, nem? Javítsatok ki, ha tévedek.
A másik ,hogy a P. 5344.-ben ez: "amiből készült hasábot a prizma másik oldalához illesztve a törési szög az ábra szerint α/2" áll a feladat szövegében. De a megoldás így számol: "Ha a prizmából kilépő fény törési szöge 16,6∘"... A feladat szövege alapján az
üvegből kilépő fény törési szöge α/2, legalábbis szerintem. És akkor a törésmutatója az üvegnek a sinus(béta) és a sinus (α/2 ) hányadosa.
|
|
| [1147] Tashi | 2021-08-17 19:03:14 |
 Part 2.
We prove that \(\displaystyle 1\leqslant r\leqslant p-2\Rightarrow
P(1)\equiv 0\).
We note that
\(\displaystyle
\widehat{x}_1,..., \widehat{x}_n \text{ are roots (in \(\displaystyle \mathbb{Z}_p\)) of the polynomial } P\tag{4}
\)
First, we prove the following proposition by induction on \(\displaystyle k\in
\mathbb{Z}, k\geqslant 1\):
\(\displaystyle \mathcal{P}(k): \;\; k\binom{r}{k}=r\sum_{j=0}^{k-1}
(-1)^{k-j+1}\binom{r}{j}.\)
Induction Base. \(\displaystyle k=1: \; \binom{r}{1}=r\cdot (-1)^2\binom{r}{0}\).
Induction Step. \(\displaystyle k\mapsto (k+1)\). Using induction hypothesis, we compute
\(\displaystyle
(k+1)\binom{r}{k+1}
=(k+1)\frac{r-k}{k+1}\binom{r}{k}=
r\binom{r}{k}-k\binom{r}{k}\)
\(\displaystyle =r\binom{r}{k}-r\sum_{j=0}^{k-1}(-1)^{k-j+1}\binom{r}{j}
=r\sum_{j=0}^k(-1)^{k-j+2}\binom{r}{j}.
\)
Induction finished.
Secondly, we prove that \(\displaystyle e_k\equiv\binom{r}{k}\) by induction on \(\displaystyle k, 1\leqslant k\leqslant p-2\).
Induction Base is trivial.
Induction Step. \(\displaystyle k\mapsto (k+1)\). Because \(\displaystyle k+1\leqslant p-2\) and hypothesis it follows that for each \(\displaystyle 1\leqslant i\leqslant k+1\) we have \(\displaystyle s_i\equiv r\). From this and \(\displaystyle (3)\) it follows that
\(\displaystyle
(k+1)e_{k+1}\equiv r\sum_{i=1}^{k+1}(-1)^{i-1}e_{k+1-i}\equiv r
\sum_{I=1}^{k+1}(-1)^{i-1}\binom{r}{k+1-i}\)
\(\displaystyle \equiv
r\sum_{j=0}^{k}(-1)^{k-j+1}\binom{r}{j}\stackrel{\mathcal{P}}{=}(k+1)
\binom{r}{k+1},\)
which implies \(\displaystyle e_{k+1}\equiv\binom{r}{k+1}\). Induction finished. Hence
\(\displaystyle
\forall k, \; 1\leqslant k\leqslant p-2\Rightarrow e_k\equiv\binom{r}{k}\tag{5}
\)
By \(\displaystyle (5)\) for \(\displaystyle k=r+1\leqslant p-2\) it follows that
\(\displaystyle
e_{r+1}\equiv 0\tag{6}
\)
From the Newton-Girard identities in second case it follows that
\(\displaystyle
\sum_{I=1}^{p+r}(-1)^{i-1}e_{p+r-i}s_i=0\tag{7}
\)
By the hypothesis \(\displaystyle \forall 1\leqslant k\leqslant p-2:\; s_k\equiv r\) and Fermat's Little Theorem it follows that for each \(\displaystyle 1\leqslant k\leqslant p-2\):
\(\displaystyle s_{p+k-1}=\sum_{j=1}^nx_j^{p+k-1}=\sum_{j=1}^nx_j^{p-1}\cdot
x_j^k\equiv \sum_{j=1}^n
x_j^k=s_k\equiv r \Rightarrow\)
\(\displaystyle
s_1\equiv s_2\equiv \ldots \equiv s_{p-2}\equiv s_p\equiv\ldots\equiv
s_{2p-3}\equiv r\tag{8}
\)
From \(\displaystyle (6)\) it follows that \(\displaystyle e_{r+1}=0\), which implies \(\displaystyle e_{p+r-(p-1)}s_{p-1}=e_{r+1}s_{p-1}=0\). From this, \(\displaystyle p+r\leqslant
2p-3\) and \(\displaystyle (7)\) and \(\displaystyle (8)\) it follows that \(\displaystyle 0\equiv
r\sum_{i=1}^{p+r}(-1)^{i-1}e_{p+r-i}\). Because \(\displaystyle r\neq 0\) it follows that
\(\displaystyle 0\equiv
\sum_{i=1}^{p+r}(-1)^{i-1}e_{p+r-i}=e_0-e_1+e_2-\ldots+(-1)^{p+r-1}e_{p+r-1}=P(1).\)
Hence \(\displaystyle P(1)\equiv 0\).
Now, we prove by induction on \(\displaystyle r\in \{0,1,\ldots,p-3\}\) that the solutions to the problem are \(\displaystyle (\underbrace{1,1,\ldots,1}_{\times r},\underbrace{0,0,\ldots,0}_{\times
(p-1)}) \text{ and } (\underbrace{1,1,\ldots,1}_{\times
r},1,2,\ldots,p-1)\).
Induction Base is the case \(\displaystyle r=0\).
Induction Step. \(\displaystyle r\mapsto (r+1)\). Because \(\displaystyle \widehat{x}_1,...,\widehat{x}_{p+r}\) are the roots (in \(\displaystyle \mathbb{Z}_p\)) of the polinomial \(\displaystyle P\) and \(\displaystyle P(1)\equiv 0\) it follows that \(\displaystyle \widehat{1}\in
\{\widehat{x}_1,\ldots, \widehat{x}_{p+(r+1)-1}\}\).
WLOG we can assume that \(\displaystyle x_{p+r}\equiv 1\). From this and the hypothesis it follows that \(\displaystyle \forall 1\leqslant k\leqslant p-2\):
\(\displaystyle r+1 \equiv \sum_{j=1}^{p+r}x_j^k\equiv 1+\sum_{j=1}^{p+r-1}x_j^k\pmod
p.\)
From this and the induction hypothesis it follows that the solutions are
\(\displaystyle (\underbrace{1,1,...,1}_{\times
r},\underbrace{0,0,...,0}_{\times(p-1)},1)
\text{ and } (\underbrace{1,1,\ldots,1}_{\times
r},1,2,\ldots,p-1,1),\)
which finished the induction. The problem is solved!
|
| Előzmény: [1146] Tashi, 2021-08-17 19:01:47 |
|
| [1146] Tashi | 2021-08-17 19:01:47 |
 This is an alternative proof for the problem A. 792., which is based on an idea found in January (to use the Newton's identities), which I could not complete at that time.
(Because I'm authorized to post up to 5120 characters I post the solution in two parts).
Part 1. Let \(\displaystyle n=p+r-1\). Let
\(\displaystyle e_0=1,\;e_1=\sum_{i=1}^n x_i,\; e_2=\sum_{1\leqslant i<j\leqslant n}
x_ix_j,... ,\; e_n=\prod_{i=1}^ne_i.\)
Let (in \(\displaystyle \mathbb{Z}_p\)) be the polynomial \(\displaystyle P(x)=\prod_{i=1}^n(x-x_i)=\sum_{k=0}^n(-1)^{n-k}x^{k}e_{n-k}
\in \mathbb{Z}_p[x]\) (we use \(\displaystyle \mathbb{Z}_p\) instead of \(\displaystyle \mathbb{F}_p\)).
For each positive integer \(\displaystyle k\) let \(\displaystyle s_k=\sum_{j=1}^n x_j^k\). Let \(\displaystyle \mathbb{Z}_p^*=\mathbb{Z}_p\setminus \{\widehat{0}\}\). We abreviatte \(\displaystyle a\equiv b\;(\mathrm{mod} \; p)\) by \(\displaystyle a\equiv b\).
First we solve the problem in
The Case \(\displaystyle r=0\). From Newton-Girard identities it follows that
\(\displaystyle
\forall k\in \mathbb{Z}, 1\leqslant k\leqslant p-1: \; \; ke_k=
\sum_{i=1}^k (-1)^{i-1}e_{k-i}s_i \tag{1}
\)
By the hypothesis
\(\displaystyle
s_1\equiv s_2\equiv ...\equiv s_{p-2}\equiv 0 \tag{2}
\)
We prove by induction on \(\displaystyle k \in \{1,2,...,p-2\}\) that \(\displaystyle e_k\equiv 0\).
Induction Base. \(\displaystyle e_1=s_1 \equiv 0 \Rightarrow e_1\equiv 0\).
Induction Step. \(\displaystyle k \mapsto (k+1)\). From \(\displaystyle (1)\) it follows that
\(\displaystyle
(k+1)e_{k+1}=\sum_{i=1}^{k+1} (-1)^{i-1}e_{k+1-i}s_i\tag{3}
\)
Because for each \(\displaystyle 1\leqslant i\leqslant k+1\): \(\displaystyle {k+1-i}\in
\{0,1,...,k\}\), \(\displaystyle (2)\), \(\displaystyle (3)\) and because \(\displaystyle k+1\leqslant p-2\) it follows that
\(\displaystyle (k+1)e_{k+1}\equiv 0.\)
Hence \(\displaystyle e_{k+1}\equiv 0\). Induction finished.
Hence \(\displaystyle \widehat{x}_1,..., \widehat{x}_{p-1}\) are roots of the polynomial \(\displaystyle P(x)=x^{p-1}-\widehat{e}_{p-1}\) in \(\displaystyle \mathbb{Z}_p\). We have 2 sub-cases:
1. \(\displaystyle e_{p-1}\equiv 0 \Rightarrow \widehat{x}_1,...,
\widehat{x}_{p-1}\) are roots of the polynomial \(\displaystyle x^{p-1}\) in \(\displaystyle \mathbb{Z}_p\), which implies \(\displaystyle x_1\equiv x_2\equiv
...\equiv x_{p-1}\equiv 0\).
2. \(\displaystyle e_{p-1}\not\equiv 0\). Then \(\displaystyle x_i\not\equiv 0\) for each \(\displaystyle 1\leqslant i\leqslant p-1\).
By Fermat's Little Theorem \(\displaystyle \forall t\in \mathbb{Z}_p^*\): \(\displaystyle t^{p-1}\equiv 1\) it follows that \(\displaystyle P(x)=x^{p-1}-\widehat{e}_{p-1}\) have roots in \(\displaystyle \mathbb{Z}_p\) if and only if \(\displaystyle e_{p-1}\equiv 1\). Hence
\(\displaystyle x^{p-1}-\widehat{e}_{p-1}=x^{p-1}-\widehat{1}=
(x-\widehat{1})(x-\widehat{2})...(x-\widehat{p-1}),\)
which implies \(\displaystyle \{\widehat{x}_1,\ldots,
\widehat{x}_{p-1}\}=\mathbb{Z}_p^*\).
Case \(\displaystyle r=0\) finished.
|
|
|
|
|
|
|
| [1140] Róbert Gida | 2021-08-15 20:38:05 |
 Ha \(\displaystyle x=0\) vagy \(\displaystyle y=0\) akkor az állítás trivi. Egyébként feltehető, hogy \(\displaystyle x*y=1\) vagy \(\displaystyle x*y=-1\) ez is trivi. Tehát egy változótól meg tudnánk szabadulni, még nehéz marad a probléma, nem?
|
| Előzmény: [1138] sakkmath, 2021-08-14 20:01:50 |
|
| [1139] Varga Boldizsár | 2021-08-15 16:35:59 |
 Kicsit késve, de én is felteszek egy megoldás(vázlato)t az A.796. feladatra.
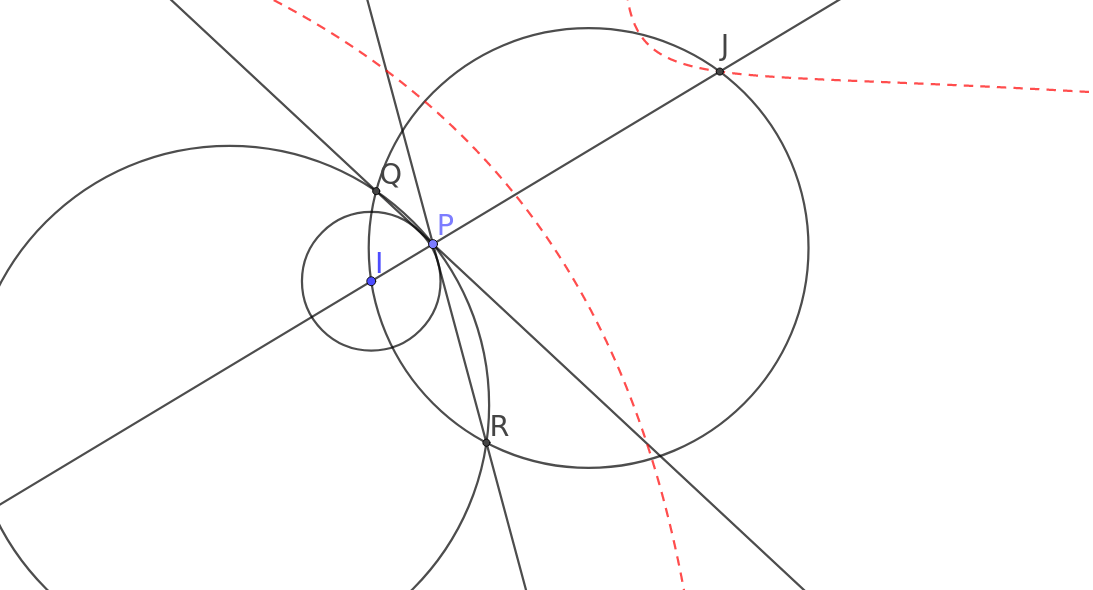
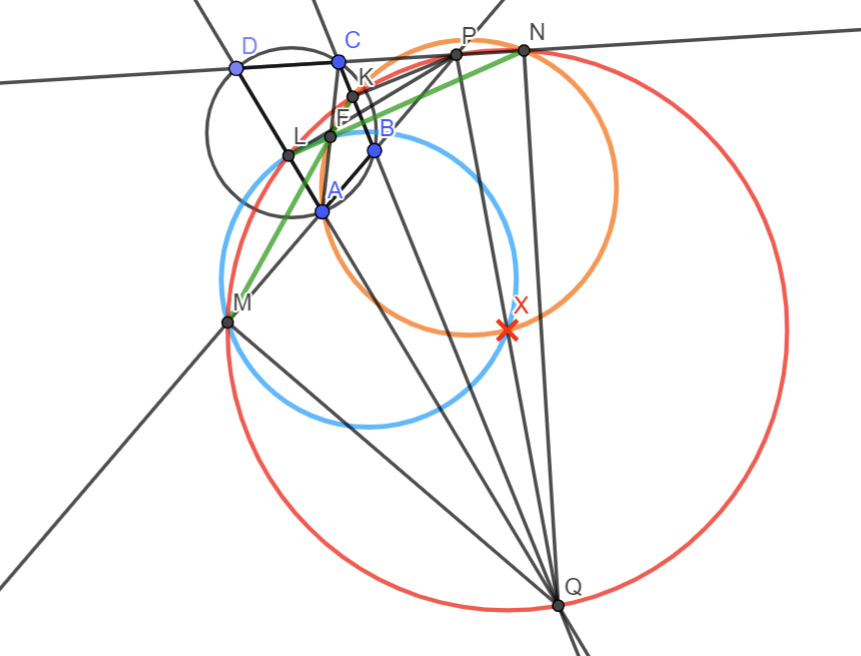
Megoldás(vázlat). Az ábrának számtalan különböző példánya lehet, ezért a diszkusszió elkerülése érdekében végig irányított szögeket fogunk használni. (Tehát az \(\displaystyle XYZ\sphericalangle\) jelölés azt fogja jelenteni, hogy mekkora szöggel kell az \(\displaystyle XY\) egyenest elforgatni pozitív irányba, hogy az \(\displaystyle YZ\) egyenest kapjuk.) Jelölje \(\displaystyle X\) a \(\displaystyle PQ\) szakasz felezőpontját, megmutatjuk, hogy \(\displaystyle X\) az \(\displaystyle FKN\) és \(\displaystyle FLM\) körök második metszéspontja. Először is megjegyezzük, hogy a Thalesz-tétel miatt \(\displaystyle K,L,M,N\) a \(\displaystyle PQ\) szakasz fölé emelt Thalesz-körön vannak, és ennek a középpontja \(\displaystyle X.\) Két lemma adja a megoldás kulcsát.
Első lemma. A \(\displaystyle KMF,\) illetve \(\displaystyle LFN\) ponthármasok kollineárisok.
Bizonyítás. A szimmetriára szorítkozva elég belátnunk, hogy \(\displaystyle KMF\) egy egyenesre esnek. Irányított szögekkel: \(\displaystyle PBK\sphericalangle=-QBM\sphericalangle,\) illetve \(\displaystyle KCP\sphericalangle=BCP\sphericalangle=BCD\sphericalangle=BAD\sphericalangle=MAQ\sphericalangle.\) Így tehát \(\displaystyle PKB\triangle\sim{QMB}\triangle,\) és ezek ellentétetes körüljárási irányúak, illetve \(\displaystyle PKC\triangle\sim{QMA}\triangle,\) és ezek azonos körüljárási irányúak. Ebből adódik, hogy -előjeles szakaszokkal- \(\displaystyle \frac{BK}{KC}=-\frac{BM}{MA}.\) Tehát \(\displaystyle \frac{AF}{FC}\cdot{\frac{CK}{KB}}\cdot{\frac{BM}{MA}}=-1,\) amiből a Menelaosz-tétel megfordítása miatt az következik, hogy \(\displaystyle K,M\) és \(\displaystyle F\) egy egyenesre esnek. Hasonlóképp látható be ez az \(\displaystyle LFN\) pnthármasról is. \(\displaystyle \square\)
Második lemma. \(\displaystyle KL\parallel{MN}.\)
Bizonyítás. Ha sikerülne belátni, hogy \(\displaystyle MNP\sphericalangle+NPK\sphericalangle=LKP\sphericalangle,\) akkor teljesülne a bizonyítandó, hiszen \(\displaystyle LKP\sphericalangle=-PKL\sphericalangle,\) így \(\displaystyle MNP\sphericalangle+NPK\sphericalangle+PKL\sphericalangle=0°,\) azaz \(\displaystyle MN\) és \(\displaystyle KL\) párhuzamosak. Mivel (a kerületi szögek irányított szögekre vonatkozó tétele alapján) \(\displaystyle MNP\sphericalangle=MQP\sphericalangle\) és \(\displaystyle LKP\sphericalangle=LQP\sphericalangle,\) ezért \(\displaystyle LKP\sphericalangle-MNP\sphericalangle=LQP\sphericalangle-MQP\sphericalangle=LQM\sphericalangle.\) Így elég azt bizonyítani, hogy \(\displaystyle LQM\sphericalangle=NPK\sphericalangle.\) Legyen \(\displaystyle I=PK\cap{QN}.\) Ekkor \(\displaystyle N\) és \(\displaystyle K\) a \(\displaystyle CI\) fölé rajzolt Thalesz-körön vannak, azaz \(\displaystyle N,K,C,I\) egy körön vannak. Innen \(\displaystyle LQM\sphericalangle=90°-MAQ\sphericalangle=90°-BAD\sphericalangle=90°-BCD\sphericalangle=\) \(\displaystyle =90°-KCN\sphericalangle=90°-KIN\sphericalangle=NPK\sphericalangle.\) Ezzel a fentiek szerint beláttuk a második lemmát. \(\displaystyle \square\)
A két lemma alapján \(\displaystyle KLMN\) (nem feltétlen ilyen sorrendben a csúcsokkal) húrtrapéz, \(\displaystyle F\) a szárai vagy az átlói metszéspontja. A lemmák alapján \(\displaystyle KMN\sphericalangle=KQN\sphericalangle\) és \(\displaystyle MNL\sphericalangle=MQL\sphericalangle,\) így \(\displaystyle NFM\sphericalangle=-KQN\sphericalangle-MQL\sphericalangle.\) Mivel a szimmetria miatt a \(\displaystyle KQN\sphericalangle\) és \(\displaystyle MQN\sphericalangle\) nagysága azonos (azonos nagyságú íven -a húrtrapéz oldala vagy átlója- nyugszanak), és irányításuk is azonos, ezért \(\displaystyle NFM\sphericalangle=NFK\sphericalangle=LFM\sphericalangle=-2KQN\sphericalangle=-2MQL\sphericalangle.\) Innen \(\displaystyle NFK\sphericalangle=2NQK\sphericalangle,\) illetve \(\displaystyle LFM\sphericalangle=2LQM\sphericalangle,\) amiből a kerületi és középponti szögek tételének megfordítása miatt az \(\displaystyle FKN\) és \(\displaystyle FLM\) körök is áthaladnak a \(\displaystyle KLMNPQ\) kör középpontján, ami az \(\displaystyle X\) pont. Ezzel az állítást beláttuk.
|
 |
| Előzmény: [1136] Lpont, 2021-08-13 19:19:18 |
|
| [1138] sakkmath | 2021-08-14 20:01:50 |
 Van-e valakinek megoldása, ötlete a 2014. áprilisi számban megjelent A. 616. feladatra?
|
|
| [1137] Tashi | 2021-08-14 08:57:52 |
 Proof for the problem A. 796.
For each triangle \(\displaystyle XYZ\) let \(\displaystyle \mathcal{C}_{XYZ}\) be the circumcircle of the triangle \(\displaystyle XYZ\).
Let \(\displaystyle A',\, Q',\) and \(\displaystyle P'\) be the midpoints of the segments \(\displaystyle [PQ],\,
[AP],\) and \(\displaystyle [AQ]\), respectively. Let \(\displaystyle \{H\}=PL \cap QM\) and \(\displaystyle \{H'\}=PK\cap QN\) be the orthocenters of the triangles \(\displaystyle APQ\) and \(\displaystyle CPQ\), respectively.
Let \(\displaystyle \mathcal{H}_1\) be the homothety with center \(\displaystyle A\) and ratio \(\displaystyle 1/2\). Let \(\displaystyle E_a\) be the midpoint of the segment \(\displaystyle [AH]\).
Because \(\displaystyle \{H\}=PL \cap QM\) and \(\displaystyle AL\perp LH,\, AM\perp MH\) it follows that the quadrilateral \(\displaystyle HLAM\) is cyclic. From this and \(\displaystyle ABCD\) is a cyclic quadrilateral it follows that
\(\displaystyle \measuredangle QHP=\measuredangle MHL=180^\circ-\measuredangle MAL=
180^\circ-\measuredangle BAD=\measuredangle BCD=\measuredangle QCP,\)
which implies that
\(\displaystyle
\text{the quadrilateral } HCPQ\text{ is cyclic} \tag{1}
\)
We note that \(\displaystyle \mathcal{H}_1(C)=F,\,
\mathcal{H}_1(H)=E_a,\,\mathcal{H}_1(Q)=P',\,\mathcal{H}_1(P)=Q'.\) From this and \(\displaystyle (1)\) it follows that \(\displaystyle \mathcal{H}_1(HCPQ)=E_aFQ'P'\) is a cyclic quadrilateral, which implies that \(\displaystyle F\) lies on the Euler circle (nine-point circle) \(\displaystyle \mathcal{E}_1\) if the triangle \(\displaystyle APQ\).
Because \(\displaystyle M\in \mathcal{E}_1\) and \(\displaystyle L\in \mathcal{E}_1\) it follows that
\(\displaystyle \mathcal{C}_{FLM}=\mathcal{E}_1 \tag{2}\)
Similarly to \(\displaystyle (2)\), using the homothety \(\displaystyle \mathcal{H}_2\) with center \(\displaystyle C\) and ratio \(\displaystyle 1/2\) we obtain that
\(\displaystyle
\mathcal{C}_{FKN}=\mathcal{E}_2 \tag{3}
\)
when \(\displaystyle \mathcal{E}_2\) is the Euler circle in the triangle \(\displaystyle CPQ\). Because \(\displaystyle A'\in \mathcal{E}_1\cap\mathcal{E}_2\) and \(\displaystyle A'\in PQ\), from \(\displaystyle (2)\) and \(\displaystyle (3)\) it follows that \(\displaystyle A'\in \mathcal{C}_{FLM}\cap\mathcal{C}_{FKN}\cap PQ,\) which implies the circumcircles of triangles \(\displaystyle FKN\) and \(\displaystyle FLM\), and the line \(\displaystyle PQ\) are concurrent.
|
| Előzmény: [1136] Lpont, 2021-08-13 19:19:18 |
|
| [1136] Lpont | 2021-08-13 19:19:18 |
 A 2021. márciusi A.796. feladatra van megoldása/ötlete valakinek?
|
|
| [1135] Berko Erzsebet | 2021-08-11 15:13:10 |
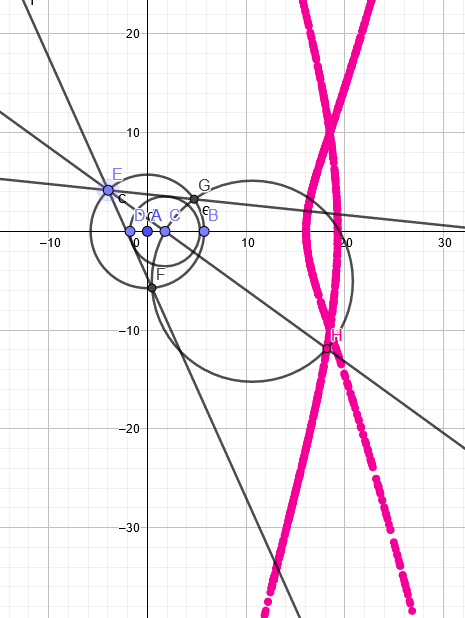
 A.779.-hez. Szemre a J pont (nálam H pont) kúpszeleten mozog. Nem ijedtem meg, hogy van olyan, hogy 2 hiperbola (?) 1-1 ága, illetve attól sem, hogy ezek metszhetik is egymást, de nem mindig metszik. Kúpszeletek származtatása? Vagy mégsem? Van köröm, csodálatos ellipszisem...
|
 |
|
| [1134] Tashi | 2021-08-09 18:43:14 |
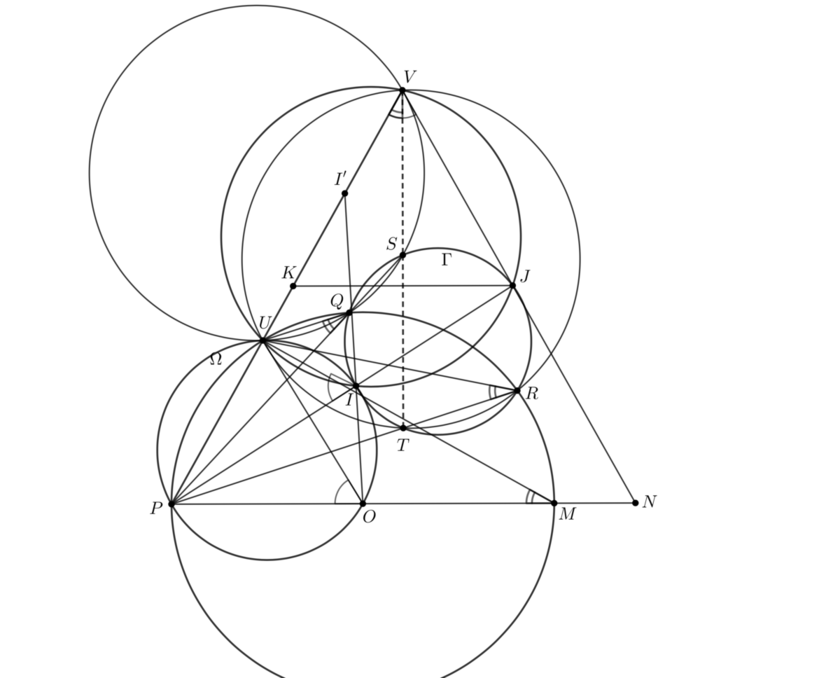
 Proof for the problem A. 779.
For a triangle \(\displaystyle XYZ\) let \(\displaystyle \mathcal{C}_{XYZ}\) be its circumcircle.
Let \(\displaystyle O\) be the center of \(\displaystyle \Omega\), \(\displaystyle \mathcal{C}_{IPO}\cap\Omega=\{P,U\}\), \(\displaystyle \mathcal{C}_{UIJ}\cap PU=\{U,V\}\), \(\displaystyle PO\cap \Omega=\{P,M\}\), \(\displaystyle VJ\cap PO=\{N\}\). Let \(\displaystyle \Gamma=\mathcal{C}_{IQR}\).
Because \(\displaystyle P\) lie on \(\displaystyle IJ\), which is the radical axis of \(\displaystyle \Gamma\) and \(\displaystyle \mathcal{C}_{UIJ}\) it follows that
\(\displaystyle PU\cdot PV= PQ\cdot PS= PT \cdot PR.\)
By Converse to power of the point it follows that
\(\displaystyle \text{ the quadrilaterals }UQSV \text{ and } UVTR \text{ are cyclic}\tag{1} \)
Because the quadrilaterals \(\displaystyle UIJV\) and \(\displaystyle POIU\) are cyclic, it follows that
\(\displaystyle \measuredangle PVN=\measuredangle UVJ=\measuredangle UIP=\measuredangle UOP.\)
From this and \(\displaystyle \measuredangle UPO=\measuredangle NPV\Rightarrow \Delta UPO\sim\Delta NPV\). From this and \(\displaystyle OP=OU\) it follows that
\(\displaystyle VP=VN\tag{2}\)
\(\displaystyle (1)\Rightarrow \measuredangle UVS=\measuredangle UQP=\measuredangle URP=\measuredangle URT=\measuredangle UVT\Rightarrow \)
\(\displaystyle V,T,S\text{ are collinear} \tag{3}\)
\(\displaystyle (1)\Rightarrow \measuredangle UVT=\measuredangle URT=\measuredangle URP=\measuredangle UMP=90^\circ-\measuredangle UPM=90^\circ-\measuredangle VPN\) \(\displaystyle \Rightarrow VT\perp PN\). From this, \(\displaystyle (1)\) and \(\displaystyle (2)\) it follows that the line \(\displaystyle V-T-S\) is \(\displaystyle V\)-height in the isosceles triangle \(\displaystyle VPN\), which implies
\(\displaystyle K\in VP\tag{4}\)
Let \(\displaystyle \psi\) be the inversion respect to the circle \(\displaystyle \Omega\) and \(\displaystyle I'=\psi(I)\). Because \(\displaystyle U, P\in \Omega\Rightarrow \psi(U)=U, \psi (P)=P\) \(\displaystyle \Rightarrow\) \(\displaystyle \psi
\left(\mathcal{C}_{UPO}\right)={PU}={PV}\) (as lines). From this and \(\displaystyle I'=\psi(I)\in
\psi\left(\mathcal{C}_{UPO}\right)\) it follows that \(\displaystyle I'\in PV\). From this and \(\displaystyle (4)\) it follows that \(\displaystyle I'\in PK\). Because \(\displaystyle I'\) is a fixed point, the problem is solved!
Remark. If I'm not mistaken, the condition that \(\displaystyle PQ\) and \(\displaystyle PR\) are tangent to \(\displaystyle \omega\) is superfluous.
|
 |
|
| [1133] HoA | 2021-08-09 01:00:14 |
 Lényegében ugyanez a megoldás adódik csak más logikai sorrendben, ha a feladatot az 1969/4 számban megjelent P. 31. problémában bizonyítandó tétel egy alkalmazásának tekintjük. Ide másolom, hogy ne kelljen keresgélni.
Ha az ottani \(\displaystyle g\) egyenesnek a mi \(\displaystyle ST\) egyenesünket, \(\displaystyle P\)-nek és \(\displaystyle Q\) -nak \(\displaystyle J\)-t illetve \(\displaystyle K\)-t, az inverzió alapkörének a \(\displaystyle P\) középpontú, \(\displaystyle IQR\) kört helyben hagyó kört feleltetjük meg, akkor \(\displaystyle g_1\) -nek \(\displaystyle \Omega\), \(\displaystyle P_1\) -nek \(\displaystyle J\) inverze, \(\displaystyle I\) , \(\displaystyle Q_1\)-nek \(\displaystyle K\) inverze, - a \(\displaystyle PK\) egyenes \(\displaystyle K'\) pontja - felel meg és a tétel éppen azt mondja ki, hogy ekkor \(\displaystyle I\) nek \(\displaystyle \Omega\)-ra vonatkozó inverze \(\displaystyle K'\).
|
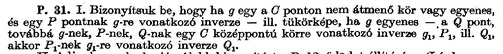 |
| Előzmény: [1125] Sinobi, 2021-08-07 22:54:33 |
|
|
|
| [1130] Berko Erzsebet | 2021-08-08 10:51:33 |
 Csináltam. Elég sok órám, napon van már ezen görbék vizsgálatában. Nemcsak ezeket a talán kúpszeletnek kinéző görbéket vizsgáltam. A nyomvonalon 5 pont kiválasztása elég bizonytalan. Most beteszem fiókba példát, de nincs elfelejtve.
|
| Előzmény: [1129] Sinobi, 2021-08-08 08:42:33 |
|
|
|
|
| [1126] Berko Erzsebet | 2021-08-08 07:00:54 |
 A kicsi kör és a körérintők helyett 3 fixpontot is felvehetünk, akár nagy körön kívül is. Tehát azt vettem észre, hogy a feladatnál maradva (tehát kicsi kör a körérintőkkel) a J pontok kúpszeletet írnak le. Kúpszeleteknek van ilyen származtatása? Tehát ez a kúpszelet téma érdekelne.
|
|
| [1125] Sinobi | 2021-08-07 22:54:33 |
 Azt állítom, hogy a keresett pont az az I pont I' inverze az Ω körre, azaz P K I' mindig egy egyenesre esnek.
Bizonyítás: Vegyük fel P-ből azt az i inverziót, az IQR kört helyben hagyja, ez Ω-t ST-be viszi, I-t J-be.
Mivel I és I' tükrösek Ω-ra, ezért a képeik tükrösek ST-re, azaz I' képe i-nél K, ami azt jelenti, hogy P, K, I' egy egyenesre esik.
Megjegyzés: sehol nem használtam ki, hogy PQ és PR érintenek egy ω kört, tetszőleges szelők lehetnek.
|
| Előzmény: [1114] sakkmath, 2021-07-19 22:51:45 |
|
| [1124] Berko Erzsebet | 2021-08-07 19:10:00 |
 Előző hozzászólásom utolsó mondata. Eredetileg nem ezt akartam írni. Kiderítettem az okát, hogy amit korábban láttam, azt utána miért nem. I mellett is nézhetünk pontot. Nekem a nagy kör középpontja az origó, a kicsi kör középpontja az x tengelyen van. Ha I mellett úgy veszem fel a három fix pont közül az egyiket, hogy az nincs a centrálison, akkor nem a tengelyen kell várnom azt a bizonyos pontot:) Elsőre valószínű a centrálison vettem fel egy fixpontot I környezetében, utána az ellenőrzéskor, meg nem.
|
|