| [94] Hardre | 2005-08-24 19:03:14 |
 Ha valaki meg tudta rendesen csinálni a P. 3811. feladatot, írja le pls hogy, mert én elakadtam.
Mégpedig ott, hogy a mágneses térbe ér a részecske. Felírtam a rá ható erőket, felbontottam komponensekre, de csak az éppen megtett út/sebesség/idő függvényében. Ha a megtett utat veszem változónak, akkor az a baj, hogy y(x) függvény általános ívhosszára olyan képlet van, amit itt sztem nem érdemes felhasználni. Akárhogy írom fel; a gond mindig a pálya függvényének meghatározása. Hiába tudom a 2 komponensének 2. deriváltját, abból túl bonyolult dolgok jönnek ki, mert sztem van vmi amire nem jöttem eddig rá.
|
|
|
|
| [90] Szabó Dani | 2005-03-10 14:44:53 |
 Valaki tegye fel a P. 3754. feladat megoldását!
|
|
| [89] rizs | 2005-03-09 14:46:40 |
 hát,a 2 egyenlet összegét rendezve csupa teljes négyzet jön ki, és onnan x=2, y=3.
|
|
| [88] jenei.attila | 2005-03-09 13:51:09 |
 Oldjuk meg a Lórántfy által kitűzött B.3790 feladatot. Nekem van egy megoldásom, kíváncsi vagyok, ti hogy oldjátok meg.
|
|
| [87] Káli gúla | 2005-03-06 19:08:40 |
 Kedves Balázs!
Elküldtem mailben azokat az oldalakat a Matematikai Lapokból, amik a feladathoz kapcsolódnak. A téglás pakolásokról az interneten is találhatsz cikkeket:
http://www-math.mit.edu/~rstan/transparencies/tilings.pdf
http://www.math.uni-bielefeld.de/~sillke/POLYCUBE/PROOF/deBruijn/filling-boxes-with-bricks.pdf
http://www.mrlonline.org/mrl/1994-001-005/1994-001-005-003.pdf
http://www.combinatorics.org/Volume_4/PDF/v4i2r12.pdf
|
| Előzmény: [86] Strenner Balázs, 2005-03-05 21:14:06 |
|
| [86] Strenner Balázs | 2005-03-05 21:14:06 |
 Hello!
Nagyon szép a megoldás, sokkal általánosabb, mint a feladat. Én is hasonló dolgokkal próbálkoztam: vetületekkel, csak nem tudtam elszakadni a kockától, de ez a szétszeletelés nagyon leleményes. Érdekelne az a Kömal-cikk, amiben ezzel foglalkoznak, de nem találtam meg. Biztos, hogy jó az év?
|
| Előzmény: [85] Káli gúla, 2005-02-27 21:48:19 |
|
| [85] Káli gúla | 2005-02-27 21:48:19 |
 Hello!
Legyen a1,...,an N. Tegyünk az n-dimenziós rács pontjaiba egy-egy lámpát. Az i-edik tengellyel párhuzamosan lépésenként ai db szomszédos lámpa állapotát megváltoztathatjuk. Ha kezdetben minden lámpa 0, és véges sok lépés után egy b1,...,bn élű B téglában (és csak ott) minden lámpa ég, akkor van olyan i N. Tegyünk az n-dimenziós rács pontjaiba egy-egy lámpát. Az i-edik tengellyel párhuzamosan lépésenként ai db szomszédos lámpa állapotát megváltoztathatjuk. Ha kezdetben minden lámpa 0, és véges sok lépés után egy b1,...,bn élű B téglában (és csak ott) minden lámpa ég, akkor van olyan i n, amire ai|bi. n, amire ai|bi.
Bizonyítás indukcióval. n=1-re az állítás igaz. Tegyük fel, hogy an nem osztója bn-nek. Legyen L a B téglának az n-edik tengelyre merőleges alsó lapja, ez tehát egy b1,...,bn-1 élhosszúságú, n-1 dimenziós tégla. Elég belátni, hogy L-ben maradva is minden lámpát át lehet állítani, ekkor ugyanis az indukciós feltevés szerint ai|bi-nek kell teljesülni valamilyen i n-1-re. Tekintsük B-ben az L-lel párhuzamos bn db réteg közül azokat, amiknek a távolsága L-től n-1-re. Tekintsük B-ben az L-lel párhuzamos bn db réteg közül azokat, amiknek a távolsága L-től  0 (mod an) vagy 0 (mod an) vagy  -1 (mod an). Szorítkozzunk a B kivilágításánál használt csíkok közül azokra, amiket ezek a rétegek tartalmaznak, és vegyük ezeknek a csíkoknak az L-re eső vetületeit (eltoltjait). Belátjuk, hogy minden x -1 (mod an). Szorítkozzunk a B kivilágításánál használt csíkok közül azokra, amiket ezek a rétegek tartalmaznak, és vegyük ezeknek a csíkoknak az L-re eső vetületeit (eltoltjait). Belátjuk, hogy minden x L-beli pontot páratlan sok vetületi csík fog fedni. an nem osztja bn miatt a 0 maradékosztályban eggyel több réteg van, mint a (-1) maradékosztályban, azaz a tekintett rétegek száma páratlan, az ide eső, x feletti pontok B-beli multiplicitása is páratlan volt, így ezen pontok multiplicitásainak összege páratlan. Az összegből el kell hagyni az L-re merőleges, an hosszúságú csíkokat, de ezek mind pontosan két x feletti pontot tartalmaznak, ezért a paritás továbbra is páratlan marad. L-beli pontot páratlan sok vetületi csík fog fedni. an nem osztja bn miatt a 0 maradékosztályban eggyel több réteg van, mint a (-1) maradékosztályban, azaz a tekintett rétegek száma páratlan, az ide eső, x feletti pontok B-beli multiplicitása is páratlan volt, így ezen pontok multiplicitásainak összege páratlan. Az összegből el kell hagyni az L-re merőleges, an hosszúságú csíkokat, de ezek mind pontosan két x feletti pontot tartalmaznak, ezért a paritás továbbra is páratlan marad.
(1) A feladatra a nemleges válasz egyszerűen következik, mert a 2x2x2-es kockákat az x1, a 3x3x3-asakat a x2, a 7x7x7-eseket az x3 tengellyel párhuzamos csíkokra bonthatnánk, és a 2005 egyik hosszal sem osztható.
(2) A feladathoz ugyan nem kell, de a csíkok nemcsak B részhalmazai lehetnek. A bizonyításban semmi újat nem kell mondani.
(3) Ehhez hasonló feladat jelent meg a Matematikai Lapok Feladatrovatában (1962/3-4, pp 314-317.), a fenti gondolatmenet is az ottani egyik megoldás mintájára készült. A kérdéskör állítólag úgy jött elő, hogy N. G. De Bruijn 7 éves kisfia megfigyelte, hogy 1x2x4-es téglákkal nem lehet egy 6x6x6-os ládát kitölteni.
|
| Előzmény: [84] SAMBUCA, 2005-02-22 03:32:47 |
|
| [84] SAMBUCA | 2005-02-22 03:32:47 |
 Na hell!
Ha vakinek van megoldása az A.363.-ra akkor beírhatná. Nagyon kiváncsi lennék...
SAMBUCA
|
|
| [83] Szabó Dániel | 2005-02-19 20:00:21 |
 Visszatérve a P. 3722. feladatra, melynek megoldása most jelent meg a KöMal-ban: az itt és Pecu által említett megoldásnál van egy egyszerűbb is. A tömegek és a tömegközépponttól való távolságok fordítottan arányosak.
|
|
|
| [81] SAMBUCA | 2005-02-18 15:17:54 |
 Helló!
Szerintem a feladat simán általánosítható n dimenzióra úgy, hogy a megfelelő méretű n-dimenziós kockát megfelelő méretű (n-1) dimenziós kockákkal fedjük le.
Ui. Kiváncsi lennék, hogy a megoldók hogyan oldották meg, de ezzel szerintem még várjunk 1-2 napot.
SAMBUCA (vajon ki???   ) )
|
| Előzmény: [80] Strenner Balázs, 2005-02-18 10:58:28 |
|
| [80] Strenner Balázs | 2005-02-18 10:58:28 |
 Nekem nagyon tetszett. Viszont érdekes, hogy általánosítható-e a feladat magasabb dimenziókra több kockával. Pl. n-dimnezióban n+1 kockával. Az érzésem az, hogy igen, de nem tudom biztosan. Aki tudja, megírhatja.
|
| Előzmény: [79] SAMBUCA, 2005-02-16 21:34:37 |
|
| [79] SAMBUCA | 2005-02-16 21:34:37 |
 Sziasztok!
Hogy tetszett az A pontversenyben a januári 2. feladat? :)
SAMBUCA
|
|
| [78] rizs | 2005-01-22 11:16:30 |
 a P.3735.-re godoltam :)
|
|
| [77] Pecu | 2005-01-14 14:26:57 |
 Sziasztok!
Az Iron által elkezdett hagyományt folytatva felírnám a P.3722. feladat eredményét. Ha jól emlékeszem közel 350 dolgozat érkezett, a fele lett három pontos, a másik fele pedig 0 pontos (szerintem ez lehet a másik feladat, aminek a statisztikája "megdöbbentő"), elvétve akadt csak 1 vagy 2 pontos. A baj az volt, hogy sokan azt írták, akkor lesz az A pont a súlypont, ha a háromszög és a négyzet területe megegyezik, mások pedig azt, ha a háromszög és a négyzet súlypontja egyenlő távolságra van az A ponttól. Ez pedig nem igaz, hiszen ha a két terület egyenlő, akkor a súlypontjuk nem egyenlő távolságra lesz A-tól, vagyis nem lesz 0 a forgatónyomaték, ugyanez a helyzet a másik esetben is. Szóval ezek a megoldások elvi hibásak, ezért a 0 pont. 1 vagy két pontot annak megfelelően adtam, hogy csak kisebb vagy komolyabb számolási hibák voltak a dolgozatban. A helyes megoldás az, ha a háromszög és a négyzet által az A pontra kifejtett forgatónyomatékok egyenlőségét vizsgáljuk, és a helyes b/a arány  . Remélem ez így megfelel. . Remélem ez így megfelel.
Üdv, Pecu
|
|
| [76] rizs | 2005-01-12 23:48:42 |
 hasonlóan az említett p feladathoz, a k.11. statisztikája is elég megrázó. 6 pontos dolgozat lett? :)
|
|
| [75] eron | 2005-01-12 13:52:06 |
 Sziasztok! Ironnak sikerült olyan hosszú téli álmot aludnia, hogy elfelejtette a jelszavát, így eron néven született újjá.. Néhány lelkes kritikus jelezte, hogy jó lenne, ha a javítók közül, akinek van rá lehetősége, a dolgozatok lepontozása után az általa javított megoldások típushibáiról, és a jó megoldásról szólna néhány szót. El is kezdeném :) A P. 3725.-ös feladatra több mint 400-an küldtek megoldást, ebből 10 4-pontos, >200 3, >100 2, a többi 1 és 0, ez engem is feldühítene első ránézésre :). Az történt ugyanis, hogy az emberek elég nagy többsége a víz hőtágulását a megadott tartományban állandónak tekintette, ami a sűrűségértékeket megnézve nem teljesen igaz. Ha emellett minden jó, akkor kapott vki 3 pontot. Pontos eredmény úgy adódna, ha azt is beleszámolnánk, hogy a kifolyó víz sűrűsége, hőmérséklete, stb. nem állandó, ha a kifolyás folyamatával számolunk, akkor ez elég hosszadalmas; egészen egyszerűen fel lehet azt írni, hogy a 20 fokos vízsűrűséggel mekkora tömegű víz fér el az eredeti térfogatú bojlerbe, majd 80fokon, a már kitágult bojlerben (hiszen az is tágul, különben minek mondták volna meg, hogy acél?) mekkora tömegű a víz. A maradék tömeg nyilván kifolyik, ennek a térfogatát pedig lehet becsülgetni, de nem változtat sokat a végeredményen, hogy változik a hőmérséklete. Annak ellenére, hogy a víz hőtágulási együtthatójának a változása a megadott tartományban aránylag nem túl nagy, a fél literrel összehasonlítva számottevő különbség adódik: a "3 pontos" módszer a víz új térfogatára 0,68l körüli értéket ad, a valódi érték pedig (emlékeim szerint) 2,2l körül van, vagyis arányaiban nagy az eltérés. További pontlevonás: ha a tartály tágulásával nem foglalkozik vki, elszámolja, vagy elvi hiba.
Remélem, ez korrekt. Üdv: Áron
|
|
|
| [73] Strenner Balázs | 2004-11-11 09:30:40 |
 Kedves Géza!
Sokat gondolkoztam az A.344. feladaton, de végre sikerült találnom egy megolást. Remélem jó.
Tegyük fel, hogy van egy zárt hurok. A 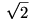 hosszú oldalakat figyelmen kívül hagyva egy kígyószerű képződményt kapunk, aminek van egy belső határvonala (az ábrán piros), ami gráfos nyelven szólva nem tartalmazhat kört(mivel a hurok lyukmentes), tehát "fa". Ezért a fán haladva egyszer elérünk egy olyan rácspontba, amiből 3 irányba legfeljebb 1-1 ág indul, de összesen legalább 1. Vizsgáljuk ezeket a végződéseket. Az ábrán feltüntettem a szóba jövőket, ezek közül csak a bekarikázott lehetséges. Ekkor viszont a 3 csempét ki lehet cserélni 1-re, amivel rövidebb hurkot kapunk. És kész a végtelen leszállás. hosszú oldalakat figyelmen kívül hagyva egy kígyószerű képződményt kapunk, aminek van egy belső határvonala (az ábrán piros), ami gráfos nyelven szólva nem tartalmazhat kört(mivel a hurok lyukmentes), tehát "fa". Ezért a fán haladva egyszer elérünk egy olyan rácspontba, amiből 3 irányba legfeljebb 1-1 ág indul, de összesen legalább 1. Vizsgáljuk ezeket a végződéseket. Az ábrán feltüntettem a szóba jövőket, ezek közül csak a bekarikázott lehetséges. Ekkor viszont a 3 csempét ki lehet cserélni 1-re, amivel rövidebb hurkot kapunk. És kész a végtelen leszállás.
|
 |
| Előzmény: [60] Kós Géza, 2004-06-04 10:25:03 |
|
| [72] jenei.attila | 2004-08-17 14:24:27 |
 Én is a rekurzió karakterisztikus egyenletéből kaptam a zárt alakot, amelynek komplex gyökei vannak, és a komplex számok hatványozására vonatkozó Moivre képletből (azt hiszem így hívják) adódik a zárt alak. Közvetlenül felismerni pedig szerintem nagyon nehéz lenne. A Csebisev polinomokkal való összefüggést esetleg észre lehet venni, de azok koszinuszos előállítását is ismerni kell.
|
| Előzmény: [71] Kós Géza, 2004-08-17 14:13:35 |
|
| [71] Kós Géza | 2004-08-17 14:13:35 |
 A nevezőből az következik, hogy an értéke sohasem lesz pontosan 1, mert soha sem lesz egész szám.
A koszinuszos alak nem igazán kerülhető ki. El lehet mondani persze a megoldást úgy, hogy csak titokban tudjuk, hogy koszinuszokról van szó, de az ugyanaz.
A kérdés inkább az, hogy mennyire lehet kitalálni a koszinuszos alakot. Aki nem ismeri fel közvetlenül, az még kezelheti a sorozatot lineáris rekurzív sorozatként is, abból is kiderül. De erről inkább valaki olyan nyilatkozzon, aki meg is oldotta a feladatot. :-)
|
| Előzmény: [70] jenei.attila, 2004-08-17 13:39:49 |
|
| [70] jenei.attila | 2004-08-17 13:39:49 |
 Igaz. Ezek szerint az an=cos(n*arccos(1/3)) összefüggésből azonnal következik a feladat állítása. Az igaz, hogy a rekurzióból kiolvasható hogy an nevezője 3n, de ebből hogyan következik a feladat állítása? Van -e olyan megoldás, ami nem használja fel a koszinuszos zárt alakot?
|
| Előzmény: [69] Kós Géza, 2004-08-17 12:57:07 |
|
| [69] Kós Géza | 2004-08-17 12:57:07 |
 Szia Attila,
A feladat megoldásához nem szükséges bebizonyítani, hogy 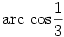 irracionális. Ha racionális lenne, akkor az (an) sorozatban végtelen sokszor szerepelne az 1, és az állítás akkor is igaz volna. irracionális. Ha racionális lenne, akkor az (an) sorozatban végtelen sokszor szerepelne az 1, és az állítás akkor is igaz volna.
Abban igazad van, hogy a Csebisev-polinomok egy kis kerülőt jelentenek. A rekurzióból --- ami a feladat szövegében is szerepelt --- közvetlenül kiolvasható, hogy an nevezője 3n.
|
| Előzmény: [68] jenei.attila, 2004-08-17 11:00:07 |
|





 N. Tegyünk az n-dimenziós rács pontjaiba egy-egy lámpát. Az i-edik tengellyel párhuzamosan lépésenként ai db szomszédos lámpa állapotát megváltoztathatjuk. Ha kezdetben minden lámpa 0, és véges sok lépés után egy b1,...,bn élű B téglában (és csak ott) minden lámpa ég, akkor van olyan i
N. Tegyünk az n-dimenziós rács pontjaiba egy-egy lámpát. Az i-edik tengellyel párhuzamosan lépésenként ai db szomszédos lámpa állapotát megváltoztathatjuk. Ha kezdetben minden lámpa 0, és véges sok lépés után egy b1,...,bn élű B téglában (és csak ott) minden lámpa ég, akkor van olyan i n, amire ai|bi.
n, amire ai|bi.  0 (mod an) vagy
0 (mod an) vagy 

 )
)

