| [902] nadorp | 2014-06-25 13:31:29 |
 A Fálesz Mihály által [900]-ban leírt egyenlőtlenséget bizonyítjuk, ebből c=1 esetén következik A616.
| &tex;\displaystyle a^{x^2} b^{y^2} c^{z^2} \left(\frac{a+b}2\right)^{2xy} \left(\frac{a+c}2\right)^{2xz} \left(\frac{b+c}2\right)^{2yz} \le 1 &xet; | (1) |
Mivel x+y+z=0, ezért x,y,z közt van kettő olyan, melyek szorzata nemnegatív. Tegyük fel, hogy &tex;\displaystyle xy\geq0&xet;. (1)-et átrendezve és felhasználva, hogy z=-x-y
&tex;\displaystyle \left(\frac{4ac}{(a+c)^2}\right)^{x^2}\left(\frac{2(a+b)c}{(a+c)(b+c)}\right)^{2xy}\left(\frac{4bc}{(b+c)^2}\right)^{y^2}\leq1&xet;
Ha x+y=0, akkor nyilván teljesül az egyenlőtlenség, ellenkező esetben a fentivel ekvivalens
&tex;\displaystyle \left(\frac{4ac}{(a+c)^2}\right)^{\frac{x^2}{(x+y)^2}}\left(\frac{2(a+b)c}{(a+c)(b+c)}\right)^{\frac{2xy}{(x+y)^2}}\left(\frac{4bc}{(b+c)^2}\right)^{\frac{y^2}{(x+y)^2}}\leq1&xet;
A bal oldalra alkalmazva a súlyozott számtani és mértani közép közti összefüggést, elég belátnunk, hogy
&tex;\displaystyle \frac{4ac}{(a+c)^2}\frac{x^2}{(x+y)^2}+\frac{2(a+b)c}{(a+c)(b+c)}\frac{2xy}{(x+y)^2}+\frac{4bc}{(b+c)^2}\frac{y^2}{(x+y)^2}\leq1&xet;
&tex;\displaystyle \frac{(c-a)^2}{(a+c)^2}x^2+\frac{(c-a)(c-b)}{(a+c)(b+c)}2xy+\frac{(c-b)^2}{(b+c)^2}y^2\geq0&xet;
Ez pedig nyilvánvaló, mert a bal oldal teljes négyzet
|
| Előzmény: [901] w, 2014-06-25 09:47:16 |
|
|
|
| [899] Fálesz Mihály | 2014-06-24 22:39:53 |
 Kedves Péter,
A feladatnak van egy szimmetrikus változata: Ha &tex;\displaystyle a,b,c>0&xet; és &tex;\displaystyle x+y+z=0&xet;, akkor
&tex;\displaystyle
a^{x^2} b^{y^2} c^{z^2}
\left(\frac{a+b}2\right)^{2xy}
\left(\frac{a+c}2\right)^{2xz}
\left(\frac{b+c}2\right)^{2yz}
\le 1.
&xet;
Ha tehát van egy elemi megoldásod az &tex;\displaystyle x,y\ge0&xet; esetre, akkor az megoldja a többi esetet is.
|
| Előzmény: [898] nadorp, 2014-06-22 19:28:36 |
|
| [898] nadorp | 2014-06-22 19:28:36 |
 Az A616-ra nem érkezett jó megoldás és még nincs fenn a hivatalos verzió. Itt egy megoldásvázlat, hibája, hogy kicsit "durva", nem középiskolás anyagot használ. Érdekelne egy elemibb megoldás, mely például a súlyozott számtani és mértani közép közti egyenlőtlenséget használja. Ebben eljutottam valameddig, de az xy<0, (1-a)(1-b)>0 esetben elakadtam.
&tex;\displaystyle \left(\frac{1+a}2\right)^{2x(x+y)}\left(\frac{1+b}2\right)^{2y(x+y)}\geq a^{x^2}b^{y^2}\left(\frac{a+b}2\right)^{2xy}&xet;, a,b >0 és x,y tetszőleges valós számok
A bizonyításban az alábbi ismert analízis fogalmakat fogjuk felhasználni:
1. Ha p és q pozitív valós számok, akkor
| &tex;\displaystyle \int_0^1\frac{dx}{\sqrt{(x+p)(x+q)}}=2\ln{\frac{\sqrt{p+1}+\sqrt{q+1}}{\sqrt p+\sqrt q}} &xet; | (1) |
2. Schwarz egyenlőtlenség. Ha f és g az [a,b] intervallumon négyzetesen integrálható függvények, akkor
| &tex;\displaystyle \left(\int_a^bf(x)g(x)dx\right)^2\leq\int_a^bf^2(x)dx\int_a^bg^2(x)dx &xet; | (2) |
Az eredeti egyenlőtlenség a=1 vagy b=1 esetén könnyen láthatóan teljesül, ezért a továbbiakban feltesszük, hogy &tex;\displaystyle a,b ~\neq1&xet;. Véve az egyenlőtlenség mindkét oldalának természetes alapú logaritmusát, majd átrendezve, az eredetivel ekvivalens
| &tex;\displaystyle x^2\ln{\frac{(1+a)^2}{4a}}+2xy\ln{\frac{(1+a)(1+b)}{2(a+b)}}+y^2\ln{\frac{(1+b)^2}{4b}}\geq0 &xet; | (3) |
Mivel
&tex;\displaystyle \ln{\frac{(1+a)^2}{4a}}>0&xet; és &tex;\displaystyle \ln{\frac{(1+b)^2}{4b}}>0&xet;, ezért (3) bizonyításához elég belátni, hogy a diszkriminánsa nempozitív, azaz
| &tex;\displaystyle \ln{\frac{(1+a)^2}{4a}}\ln{\frac{(1+b)^2}{4b}}\geq\left(\ln{\frac{(1+a)(1+b)}{2(a+b)}}\right)^2 &xet; | (4) |
Tetszőleges p>1 számra
&tex;\displaystyle \ln{p}=\int_1^p\frac{dx}x=\int_0^1\frac{p-1}{(p-1)x+1}dx=\int_0^1\frac{dx}{x+\frac1{p-1}}&xet;
ezért felhasználva a (2)-t
&tex;\displaystyle \ln{\frac{(1+a)^2}{4a}}\ln{\frac{(1+b)^2}{4b}}=\int_0^1\frac{dx}{x+\frac{4a}{(a-1)^2}}\int_0^1\frac{dx}{x+\frac{4b}{(b-1)^2}}\geq\left(\int_0^1\frac{dx}{\sqrt{\left(x+\frac{4a}{(a-1)^2}\right)\left(x+\frac{4b}{(b-1)^2}\right)}}\right)^2&xet;
A számolást nem részletezve, felhasználva (1)-et kapjuk
&tex;\displaystyle \ln{\frac{(1+a)^2}{4a}}\ln{\frac{(1+b)^2}{4b}}\geq\left(2\ln{\frac{(1+a)|b-1|+(1+b)|a-1|}{2\sqrt a|b-1|+2\sqrt b|a-1|}}\right)^2&xet;
De
&tex;\displaystyle \frac{(1+a)|b-1|+(1+b)|a-1|}{2\sqrt a|b-1|+2\sqrt b|a-1|}=\left\{\matrix{\frac{1+\sqrt{ab}}{\sqrt a+\sqrt b} & ha & (a-1)(b-1)>0 \cr \frac{\sqrt a+\sqrt b}{1+\sqrt{ab}} & ha & (a-1)(b-1)<0}\right.&xet;
Tehát
| &tex;\displaystyle \ln{\frac{(1+a)^2}{4a}}\ln{\frac{(1+b)^2}{4b}}\geq\left(\ln{\frac{1+ab+2\sqrt{ab}}{a+b+2\sqrt{ab}}}\right)^2=\left(\ln{\frac{a+b+2\sqrt{ab}}{1+ab+2\sqrt{ab}}}\right)^2 &xet; | (5) |
Most már csak az kell észrevenni, hogy tetszőleges &tex;\displaystyle p\geq q>0&xet; és &tex;\displaystyle 0<x\leq y&xet; valós számokra
| &tex;\displaystyle \frac{p+x}{q+x}\geq\frac{p+y}{q+y} &xet; | (6) |
(5) és (6) valamint &tex;\displaystyle 2\sqrt{ab}\leq a+b&xet; alapján azonnal adódik (4).
A bizonyítás alapján látszik, hogy egyenlőség az alábbi esetekben van:
1. x=0 b=1 , a és y tetszőleges
2. y=0 a=1 , b és x tetszőleges
3. a=b=1, x és y tetszőleges
4. &tex;\displaystyle a=b\neq1&xet; és x+y=0
|
|
|
| [896] Sinobi | 2014-06-12 21:14:11 |
 Ez haromszogre hogy nezne ki? Hol eles a hatar? Beirt kor atmerojenel kevesebbel nem lehet, legkisebb magassagvonal hosszara van konstrukciom. (ahol a sav euklideszi szelesseget ertjuk)
|
| Előzmény: [882] w, 2014-06-07 16:10:35 |
|
| [895] Fálesz Mihály | 2014-06-11 15:29:32 |
 "Jól félreolvastam" Mindenkivel előfordul. ;-)
Nekem úgy tűnik, hogy a feladat nem oldható meg egyetlen mérték megoldásával.
A [891]-beli példában a két sáv két különböző szélességű is lehet, emiatt a kétszer lefedett rész bárhol lehet a négyzet belsejében. Így hát a négyzet belsejének a mértéke &tex;\displaystyle 0&xet; kellene, hogy legyen. Ugyanakkor a négyzet határát akármilyen kicsi szélességű sávokkal le lehet fedni, tehát a határ is nulla mértékű...
A feladat egy általánosabb tétel speciális esete.
|
| Előzmény: [893] w, 2014-06-10 23:24:41 |
|
| [894] w | 2014-06-10 23:26:40 |
 Jogos. Ha &tex;\displaystyle i^3\equiv j^3\mod p&xet;, akkor &tex;\displaystyle 2k+1&xet;-edik hatványra emelve, a Kis-Fermat-tétel szerint &tex;\displaystyle i\equiv j\mod p&xet; adódik.
|
| Előzmény: [891] Fálesz Mihály, 2014-06-09 23:02:53 |
|
| [893] w | 2014-06-10 23:24:41 |
 Jól félreolvastam, bocsánat. Legalább nem az indoklásban van a hiba. :-)
A feladat ennek ellenére nagyon érdekesnek tűnik. Ennél a változatnál is lehet "mértéket" adni a lefedő sávoknak, vagy csak más módszerek működnek?
Arra gondolok, hogy adok egy olyan &tex;\displaystyle f(x,y)&xet; térbeli függvénygörbét, melyre tetszőleges sáv és &tex;\displaystyle f(x,y)&xet; görbe által közrefogott térfogat (integrál) a sáv szélességével egyenesen arányos. Ahhoz, hogy ezzel a négyzet lefedéséből kiindulva tudjak becsülni, még szükségem van arra, hogy megkeressem, hogy a lefedések során mely területek lehetnek kétszer lefedve, mert azokra &tex;\displaystyle f(x,y)=0&xet; kell teljesüljön. Ha van olyan &tex;\displaystyle (x,y)&xet; pont, melyre &tex;\displaystyle f(x,y)\neq 0&xet; lehetséges, akkor még van remény a mérték megkonstruálására.
|
| Előzmény: [890] Fálesz Mihály, 2014-06-09 22:55:04 |
|
| [892] Sinobi | 2014-06-09 23:33:37 |
 "Egy sáv szélessége legyen a beleírható, a tengelyekkel párhuzamos oldalú négyzetek oldalhossza. "
Rogzitve van egy x-y koordinatarendszer, annak iranyaban a legnagyobb beleirhato negyzet a sav szelessege, es nem a ket szelso egyenes tavolsaga.
|
| Előzmény: [890] Fálesz Mihály, 2014-06-09 22:55:04 |
|
| [891] Fálesz Mihály | 2014-06-09 23:02:53 |
 A &tex;\displaystyle 3k+2&xet; esetet primitív gyök használata nélkül is meg tudod oldani.
Mi az &tex;\displaystyle x\mapsto x^3&xet; (modulo &tex;\displaystyle p&xet;) függvény inverze?
|
| Előzmény: [889] w, 2014-06-09 14:51:35 |
|
| [890] Fálesz Mihály | 2014-06-09 22:55:04 |
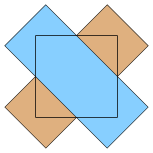
 A sáv euklideszi értelemben vett szélessége és a feladat szerinti "szélessége" átcsúszott egymásba. Egy sáv "szélessége" -- tehát a beleírható négyzet oldalhossza -- nem ugyanakkora, mint a sáv fölé emelt gömböv euklideszi értelemben vett vastagsága.
Egy &tex;\displaystyle 2r&xet; sugarú kört le lehet fedni egy &tex;\displaystyle 45^\circ&xet; irányú, euklideszi értelemben &tex;\displaystyle 2r&xet; széles sávval, de a feladatban definiált szélessége ennek a sávnak csupán &tex;\displaystyle \sqrt2r&xet;.
Az ábrán két &tex;\displaystyle 1/2&xet; "szélességű" sáv fedi le az egységnégyzetet.
|
 |
| Előzmény: [888] w, 2014-06-09 09:39:24 |
|
| [889] w | 2014-06-09 14:51:35 |
 Ja értem. Szép gondolat, köszönöm.
Könnyen belátható, hogy &tex;\displaystyle S_k=\sum_{x=1}^p x^k&xet; osztható &tex;\displaystyle p&xet;-vel, ha &tex;\displaystyle 0\le k<p-1&xet; egész szám. (Indukcióval, a &tex;\displaystyle \sum_{n=1}^p\binom n k=\binom{p+1}{k+1}&xet; azonosság segítségével.) A Kis-Fermat-tétel szerint azonban &tex;\displaystyle S_{p-1}&xet; már nem osztható &tex;\displaystyle p&xet;-vel. Ez ellentmondást jelent, hisz egyfelől &tex;\displaystyle f(x)^{\frac{p-1}3}&xet; &tex;\displaystyle (p-1)&xet;-edfokú polinom &tex;\displaystyle Z_p[x]&xet;-ben, másfelől a feltétel szerint &tex;\displaystyle \sum_{x=1}^{p}f(x)^{\frac{p-1}3}\equiv \sum_{x=1}^px^{\frac{p-1}3}\equiv 0\mod p&xet;.
|
| Előzmény: [885] Fálesz Mihály, 2014-06-08 21:00:46 |
|
| [888] w | 2014-06-09 09:39:24 |
 Tudom, hogy egy ilyen nehéz feladat megoldása nem szokott ilyen simán kijönni, de a becslés iránya szerintem rendben van. Ha én egy &tex;\displaystyle d&xet; széles sávot veszek, lecseréltem őt a körlap fedésében résztvevő &tex;\displaystyle d'\le d&xet; széles részsávjára, ami pontosan egy &tex;\displaystyle \pi r d'&xet; széles félgömbövet jelent. A gömböv lefedéséből pedig &tex;\displaystyle \sum \pi r d'=lefedett+tobbszorlefedett\ge lefedett=2\pi r^2&xet;, ahonnan &tex;\displaystyle \sum d \ge \sum d'\ge 2r&xet; adódik. (Zavaró módon írtam le azt a részt, hogy "minden &tex;\displaystyle i&xet;-re a &tex;\displaystyle d_i&xet; széles sáv legfeljebb &tex;\displaystyle \pi rd_i&xet; felszínű gömbövnek felel meg".)
Ha mutatsz egy olyan lefedést, ahol a sávok szélességeinek összege egyenlő a négyzet oldalával, és van olyan körön belüli rész, amit kétszer fedtünk le, akkor (is) biztos hibás a "megoldásom", csak látni szeretném benne a hibát.
|
| Előzmény: [886] Fálesz Mihály, 2014-06-08 21:16:32 |
|
|
| [886] Fálesz Mihály | 2014-06-08 21:16:32 |
 Nem. A gömbövök vastagságárára és felszínére felső helyett alsó becslésed van.
Btw a négyzetnek olyan fedése is van, ahol a sávok szélességeinek összege egyenlő a négyzet oldalával, és van olyan része a négyzetnek, amit készeresen fedünk le.
|
| Előzmény: [883] w, 2014-06-07 16:14:27 |
|
|
| [884] w | 2014-06-07 23:23:01 |
 A.513. Milyen &tex;\displaystyle p&xet; prímekre van olyan harmadfokú, egész együtthatós &tex;\displaystyle f&xet; polinom, amelynek főegyütthatója nem osztható &tex;\displaystyle p&xet;-vel, és amelyre az &tex;\displaystyle f(1),f(2),...,f(p)&xet; számok páronként különböző maradékot adnak &tex;\displaystyle p&xet;-vel osztva?
Egy lehetséges megközelítés (kíváncsi vagyok, hogy van-e benne hiba, illetve hogy a kitűző erre számított-e):
Megmutatjuk, hogy ezek a prímek éppen a &tex;\displaystyle 3k+2&xet; alakúak és a &tex;\displaystyle 3&xet;.
Ha &tex;\displaystyle (p-1,3)=1&xet;, akkor az &tex;\displaystyle f(x)=x^3&xet; polinom megfelelő. Valóban, ha &tex;\displaystyle g&xet; primitív gyök modulo &tex;\displaystyle p&xet;, akkor &tex;\displaystyle g^1,\dots,g^{p-1}&xet; redukált maradékrendszer modulo &tex;\displaystyle p&xet;, ahonnan &tex;\displaystyle (p-1,3)=1&xet; miatt &tex;\displaystyle g^3,\dots,g^{3(p-1)}&xet; is redukált maradékrendszer lesz modulo &tex;\displaystyle p&xet;. Vagyis a redukált maradékrendszer köbe, így &tex;\displaystyle \{1^3,\dots,(p-1)^3\}&xet; is redukált maradékrendszer modulo &tex;\displaystyle p&xet;. Ez még a &tex;\displaystyle p^3\equiv 0&xet; maradékkal kiegészülve teljes maradékrendszert hoz létre.
Most tegyük fel, hogy van olyan &tex;\displaystyle p=3k+1&xet; prímszám és &tex;\displaystyle f(x)=ax^3+bx^2+cx+d&xet; polinom, melyre &tex;\displaystyle \{f(1),\dots,f(p)\}&xet; és &tex;\displaystyle \{1,\dots,p\}&xet; megegyezik modulo &tex;\displaystyle p&xet;, és &tex;\displaystyle (a,p)=1&xet;. Feltehető, hogy &tex;\displaystyle b&xet; és &tex;\displaystyle c&xet; sem osztható &tex;\displaystyle p&xet;-vel.*
Legyen &tex;\displaystyle g&xet; primitív gyök modulo &tex;\displaystyle p&xet;, és legyen &tex;\displaystyle r=g^k&xet;. Ekkor &tex;\displaystyle r^3=g^{3k}=g^{p-1}\equiv 1\mod p&xet; a Kis-Fermat-tétel szerint. Tekintsük azt az &tex;\displaystyle s&xet; maradékosztályt mod &tex;\displaystyle p&xet;, melyre &tex;\displaystyle b(r+1)s\equiv -c\mod p&xet;. (Ilyen létezik, hisz &tex;\displaystyle r\neq -1&xet; és &tex;\displaystyle b\neq 0&xet; mod &tex;\displaystyle p&xet;, és nem nulla, hisz &tex;\displaystyle c\neq 0&xet; mod &tex;\displaystyle p&xet;.) Ekkor
&tex;\displaystyle f(sr)-f(s)=a(s^3r^3-s^3)+b(s^2r^2-s^2)+c(sr-s)\equiv 0+bs^2(r-1)(r+1)+cs(r-1)\equiv -cs(r-1)+cs(r-1)\equiv 0\mod p,&xet;
bár &tex;\displaystyle sr\neq s&xet; mod &tex;\displaystyle p&xet;, ez tehát ellentmond a páronként inkongruens &tex;\displaystyle f&xet;-értékeknek. Így &tex;\displaystyle p=3k+1&xet; esetben nem létezik megfelelő &tex;\displaystyle f&xet; polinom. []
*Ez azért tehető fel, mert ha az &tex;\displaystyle f&xet; polinom megfelelő, akkor az
&tex;\displaystyle f(x+1)=a(x^3+3x^2+3x+1)+b(x^2+2x+1)+c(x+1)+d=ax^3+(3a+b)x^2+(3a+2b+c)x+(a+b+c+d),&xet;
&tex;\displaystyle f(x+2)=a(x^3+6x^2+12x+8)+b(x^2+4x+4)+c(x+2)+d=ax^3+(6a+b)x^2+(12a+4b+c)x+(8a+4b+2c+d)&xet;
polinomok is megfelelnek a feltételnek. Ha &tex;\displaystyle p|b&xet; volt, akkor ezekben &tex;\displaystyle x^2&xet; együtthatója relatív prím &tex;\displaystyle p&xet;-hez, és nem lehet mindkettőben &tex;\displaystyle x&xet; együtthatója &tex;\displaystyle p&xet;-vel osztható. Ha &tex;\displaystyle p|c&xet;, akkor pedig legalább egyik eltolt polinomban &tex;\displaystyle x&xet; együtthatója nem osztható &tex;\displaystyle p&xet;-vel, így ha abban &tex;\displaystyle x^2&xet; együtthatója nem osztható &tex;\displaystyle p&xet;-vel, kész, ha pedig &tex;\displaystyle p&xet;-vel osztható, akkor újra alkalmazhatjuk előbbi gondolatmenetet.
|
| Előzmény: [577] Maga Péter, 2010-10-13 09:36:25 |
|
|
| [882] w | 2014-06-07 16:10:35 |
 A.526. A síkbeli koordináta-rendszerben nevezzük sávnak az olyan tartományokat, amelyeket két párhuzamos egyenes határol. Egy sáv szélessége legyen a beleírható, a tengelyekkel párhuzamos oldalú négyzetek oldalhossza. Igazoljuk, hogy ha a &tex;\displaystyle 0\le x,y\le1&xet; egységnégyzetet lefedjük véges sok sávval, akkor ezek szélességének összege legalább 1.
Belátjuk, hogy a négyzet &tex;\displaystyle r&xet; sugarú &tex;\displaystyle k&xet; beírt körlapjának lefedéséhez is legalább &tex;\displaystyle 2r&xet; szélességösszegű sávokra van szükség.
Tekintsünk a &tex;\displaystyle k&xet; fölé írható &tex;\displaystyle G&xet; félgömböt, és feleltessük meg &tex;\displaystyle k&xet; minden &tex;\displaystyle P&xet; pontját &tex;\displaystyle G&xet; azon pontjával, aminek vetülete &tex;\displaystyle k&xet; síkján &tex;\displaystyle P&xet;. Tekintsünk tetszőleges &tex;\displaystyle d&xet; széles sávot, messük el &tex;\displaystyle k&xet;-val, és tekintsük a &tex;\displaystyle k&xet;-val közös pontjainak &tex;\displaystyle G&xet;-re eső megfeleltetettjeit. A megfeleltetett pontok egy félgömbréteget alkotnak, amelynek szélessége &tex;\displaystyle \le d&xet;. Ezen félgömbréteg felszíne tehát &tex;\displaystyle \le \pi r d&xet;.
Amennyiben a &tex;\displaystyle d_1,\dots,d_n&xet; széles sávok lefedik a teljes &tex;\displaystyle k&xet; körlapot, a sávok &tex;\displaystyle G&xet;-n lévő megfeleltetettjei lefedik a teljes &tex;\displaystyle G&xet;-t. Viszont minden &tex;\displaystyle i&xet;-re a &tex;\displaystyle d_i&xet; széles sáv legfeljebb &tex;\displaystyle \pi r d_i&xet; felszínű gömbövnek felel meg, amiért &tex;\displaystyle \sum_{i=1}^n \pi r d_i\ge A_G=2\pi r^2&xet;, leosztva &tex;\displaystyle d_1+\dots+d_n\ge 2r&xet;. Ezt akartuk belátni.
|
|
| [881] Fálesz Mihály | 2014-05-13 17:28:51 |
 Adott az &tex;\displaystyle (n+3)&xet;-dimenziós térben három vektor:
&tex;\displaystyle {\bf a}=\bigg((-1)^n\binom{n}{0};(-1)^{n-1}\binom{n}{1};
(-1)^{n-2}\binom{n}{2};
\dots;\binom{n}{n}; 0; 0 \bigg), &xet;
&tex;\displaystyle {\bf b}=\bigg(0; (-1)^n\binom{n}{0};(-1)^{n-1}\binom{n}{1};
(-1)^{n-2}\binom{n}{2};
\dots;\binom{n}{n}; 0 \bigg), &xet;
és
&tex;\displaystyle {\bf c}=\bigg(0;0; (-1)^n\binom{n}{0};(-1)^{n-1}\binom{n}{1};
(-1)^{n-2}\binom{n}{2};
\dots;\binom{n}{n} \bigg). &xet;
Határozzuk meg a &tex;\displaystyle {\bf v}&xet; vektor minimális hosszát, ha
&tex;\displaystyle {\bf a}\cdot{\bf v} = {\bf b}\cdot {\bf v} = {\bf c}\cdot {\bf v} = n!&xet;
teljesül.
|
| Előzmény: [880] w, 2014-05-13 16:30:27 |
|
| [880] w | 2014-05-13 16:30:27 |
 Köszi, ez az alapkoncepció nálam is megvolt, de nem töltöttem a feladattal elég időt, hogy kijöhessen. A két hatvány különbsége résznél megjelenő becslés már nem volt meg, az már érdekes volt.
Az A611.-re is volt néhány gondolatom. Nevezetesen ha &tex;\displaystyle \sum_{k=0}^n \binom nk p(x+k)=n!&xet;-t már tudjuk, meg még efféle azonosságokat, akkor már alkalmasan súlyozott négyzetes-számtani közepek közötti becsléssel elvileg kijön. Az első benyomás persze Csebisev-polinomok volt, de utána azok nem látszottak alkalmasnak. Előbbi sorokat viszont semmi értelme sincs beírni, mert nem vezettek megoldásra.
Úgy általában, meg voltam az ez évi pontversenyben lepve, hogy (február előtt) minden egyes A-feladatra megjelent hivatalos megoldás. Ezzel együtt furcsállom, hogy már egy ideje alig írnak ki megoldásokat a B-jelű feladatokra, a korábbi sok évvel ellentétben.
|
| Előzmény: [876] Róbert Gida, 2014-04-30 20:01:27 |
|
|
| [878] Fálesz Mihály | 2014-05-07 18:55:35 |
 Ha nem volt odaírva semmi, akkor a polinom valós együtthatós. Az abszolútérték-jelekre tényleg nincs szükség.
Btw komplex együtthatós polinomokra triviálisan ugyanaz a válasz. (Csak akkor más betűt használnánk az &tex;\displaystyle i&xet; helyett.)
|
| Előzmény: [877] Róbert Gida, 2014-05-06 19:39:15 |
|







