Fórum: "ujjgyakorlatok"

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39]

Szeretnél hozzászólni? Jelentkezz be.

[451] Lóczi Lajos

2005-11-16 20:37:51

Hogy értve pozitív?

Pl. 2x2-esnél: (ad-bc)-ben "ad" és "bc" is pozitív számok, vagy "ad" és "-bc" pozitívak?

Előzmény: [450] Róbert Gida, 2005-11-16 19:42:03

[450] Róbert Gida	2005-11-16 19:42:03
87. feladat Egy nxn-es mátrix determinánsának a kifejtésénél azt a meglepő dolgot tapasztaltuk, hogy mind az n! darab tag pozítiv, milyen n-re lehetségez ez?

[449] Lóczi Lajos	2005-11-16 12:12:26
86. feladat. Legyen n pozitív egész. Az 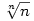$\root n \of{n}$ alakú számok között melyik a legnagyobb?

[448] Lóczi Lajos

2005-11-16 10:48:32

Az 5 az több, mint a "pár", tehát tényleg komolyabb az eszköz :)

(Leibniz nevében inkább ne legyen "t" betű.)

Előzmény: [447] Róbert Gida, 2005-11-16 00:58:20

[447] Róbert Gida

2005-11-16 00:58:20

Azért nem kellenek komoly eszközök ehhez.

Tovább számolva: legyen n>1 ekkor

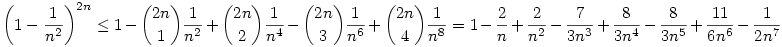
${\bigg(1-\frac 1{n^2}\bigg)}^{2n}\leq 1-\binom {2n}{1}\frac 1{n^2}+\binom {2n}{2}\frac 1{n^4}-\binom{2n}{3}\frac 1{n^6}+\binom{2n}{4}\frac 1{n^8}=1-\frac {2}{n}+\frac {2}{n^2}-\frac {7}{3n^3}+\frac {8}{3n^4}-\frac {8}{3n^5}+\frac {11}{6n^6}-\frac {1}{2n^7}$

teljesül, hiszen könnyen bizonyíthatóan Leibnitz sor a binomiális sor részletösszegeinek sorozata, így most az első 5 tag egy felső becslést ad. Az egyenlőtlenség jobb oldalára pedig alsó becslést adva: 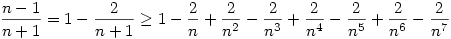$\frac {n-1}{n+1}=1-\frac {2}{n+1}\geq 1-\frac {2}{n}+\frac {2}{n^2}-\frac {2}{n^3}+\frac {2}{n^4}-\frac {2}{n^5}+\frac {2}{n^6}-\frac {2}{n^7}$ , ( ha nagy n-re akarnám belátni akkor elég lenne 4 tagot venni ) azaz elég belátni:

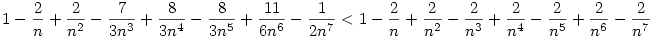
$1-\frac {2}{n}+\frac {2}{n^2}-\frac {7}{3n^3}+\frac {8}{3n^4}-\frac {8}{3n^5}+\frac {11}{6n^6}-\frac {1}{2n^7}<1-\frac {2}{n}+\frac {2}{n^2}-\frac {2}{n^3}+\frac {2}{n^4}-\frac {2}{n^5}+\frac {2}{n^6}-\frac {2}{n^7}$

Rendezve és 6n⁷-tel szorozva kell: 2n⁴-4n³+4n²+n-9>0 kell, ami n>1-re triviálisan teljesül. Így beláttuk a feladatot.

Kétségtelen kicsit számolós, de ezt szerencsére a Maple végezte el.

Előzmény: [446] Lóczi Lajos, 2005-11-15 21:53:28

[446] Lóczi Lajos

2005-11-15 21:53:28

Azért szerintem ide kicsit komolyabb eszközök kellenek, mint az első pár tag. Egy standard módszer: (n-nek semmi jelentősége, hogy egész, ezért x-et írva)

vegyünk logaritmust és rendezgessünk egy kicsit, elegendő belátni, hogy x>1 esetén

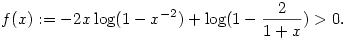
$f(x):=-2x\log (1 - x^{-2}) + \log (1 - \frac{2}{1 + x})>0.$

Könnyen látható, hogy f limesze 1-ben jobbról + $\infty$ , a végtelenben pedig 0. Továbbá

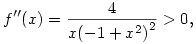
$f''(x)=\frac{4}{x{\left( -1 + x^2 \right) }^2}>0,$

tehát f konvex. Ezek miatt f pozitív és az egyenlőtlenséget beláttuk.

Előzmény: [444] Ali, 2005-11-15 14:40:53

[445] jonas

2005-11-15 20:59:39

Szép feladat.

Próbáltam a bal oldalt becsülni az első három taggal:

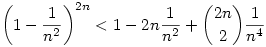
$\left(1 - \frac1{n^2}\right)^{2n} < 1 - 2n\frac1{n^2} + \binom{2n}2\frac1{n^4}$

(ha n elég nagy ), de ez már nagyobb a jobb oldalnál. Gondolkozom még rajta.

Előzmény: [444] Ali, 2005-11-15 14:40:53

[444] Ali

2005-11-15 14:40:53

Lehet, hogy nem ujjgyakorlat ?

85. feladat.

Biz.be, hogy n>1 egész esetén

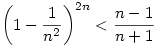
$\left(1 - \frac{1}{n^{2}}\right)^{2n} < \frac{n-1}{n+1}$

[443] Lóczi Lajos	2005-11-14 18:55:14
Valóban így van.
Előzmény: [442] Ali, 2005-11-14 16:00:17

[442] Ali	2005-11-14 16:00:17
$\alpha$ $\in$ [1/2;1] esetén monoton csökken, $\alpha$ $\in$ [0;1/2) esetén n>N( $\alpha$ )-ra monoton nő.
Előzmény: [401] Lóczi Lajos, 2005-10-30 21:36:47

[441] ágica	2005-11-12 18:58:49
Igen, ezt tényleg elfelejtettem, de szerencsére benne van :)
Előzmény: [440] Lóczi Lajos, 2005-11-12 18:41:40

[440] Lóczi Lajos	2005-11-12 18:41:40
Szép, de annyi kiegészítés még kell hozzá, hogy ellenőrizni kell: $(\sqrt{5}-1)a$ vajon benne van-e az arcsin értelmezési tartományában, azaz [-1,1]-ben.
Előzmény: [439] ágica, 2005-11-12 18:24:54

[439] ágica

2005-11-12 18:24:54

A feladatban szereplő kifejezés ekvivalens a következővel:

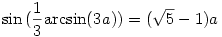
$\sin{(\frac{1}{3}\rm{arcsin}(3\it{a}))}=(\sqrt{5}-1)a$

ahol 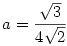$a=\frac{\sqrt{3}}{4\sqrt{2}}$ , tehát ha bebizonyítjuk, hogy ez az egyenlőség igaz, azzal az állítást is belátjuk.

A kifejezést még tovább alakíthatjuk:

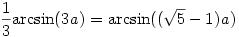
$\frac{1}{3}\rm{arcsin}(3\it{a})=\rm{arcsin}((\sqrt{5}-1)\it{a})$

Ebből pedig kapjuk, hogy

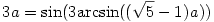
$3a=\sin({3\rm{arcsin}((\sqrt{5}-1)\it{a})})$

Trigonometrikus összefüggéseket felhasználva:

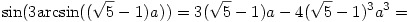
$\sin({3\rm{arcsin}((\sqrt{5}-1)\it{a})})=3(\sqrt{5}-1)a-4(\sqrt{5}-1)^{3}a^{3}=$

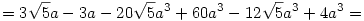
$=3\sqrt{5}a-3a-20\sqrt{5}a^{3}+60a^{3}-12\sqrt{5}a^{3}+4a^{3}=$

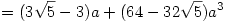
$=(3\sqrt{5}-3)a+(64-32\sqrt{5})a^{3}$

Így az előző egyenletből átrendezés és a-val való leosztás után kapjuk:

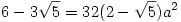
$6-3\sqrt{5}=32(2-\sqrt{5})a^{2}$

Ebbe a-t visszahelyettesítve látjuk, hogy az egyenlőség igaz, és mivel végig ekvivalens átalakításokat végeztünk, ezért az eredeti állítás is igaz volt.

Előzmény: [438] Lóczi Lajos, 2005-11-12 01:21:06

[438] Lóczi Lajos

2005-11-12 01:21:06

84. feladat. Azt állítom, hogy az aranymetszés arányszáma felírható az alábbi alakban is:

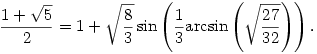
$\frac{1+\sqrt{5}}{2}=1+\sqrt{\frac{8}{3}} \sin \left(\frac{1}{3} \rm{arcsin} \left( \sqrt{\frac{27}{32}}\right)\right).$

Bizonyítsuk be vagy cáfoljuk meg az állítást.

[437] jonas	2005-11-09 22:35:59
Ezt már hallottam, de nem pont így. Ennek egy változata a 41. feladat a tesztversenyben.
Előzmény: [428] Gubbubu, 2005-11-09 13:46:47

[436] ágica	2005-11-09 18:09:50
Hát be kell vallanom hogy ennek a bizonyításáról fogalmam sincs, de majd megpróbálok utánanézni :)
Előzmény: [427] Lóczi Lajos, 2005-11-09 11:26:20

[435] Káli gúla	2005-11-09 16:00:42
A konvergenciához valahogy be kell látni (ld. 424), hogy a szomszédos törtek különbségében a számláló 1. Ebből --csak a kacifántosság kedvéért-- egyszerűen belátható, hogy a limesz, azaz 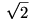$\sqrt2$ irracionális.
Előzmény: [432] Ali, 2005-11-09 15:10:08

[434] nadorp	2005-11-09 15:36:07
Bocs,nem láttam az előző négy hozzászólást (éppen TeX-eltem). Ennek tudtában nem részletezek ennyit.

[433] nadorp

2005-11-09 15:29:46

Ez a megoldás csak egy adalék, hiszen a példát már megoldottátok. Úgy rémlik, hogy általános esetben is valami hasonló módszerrel kezelik a lánctörteket.

Könnyű látni, hogy igaz az alábbi két állítás:

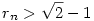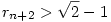
1. Ha $r_n>\sqrt2-1$ , akkor r_n>r_n+2 és $r_{n+2}>\sqrt2-1$

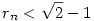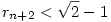
2. Ha $r_n<\sqrt2-1$ , akkor r_n<r_n+2 és $r_{n+2}<\sqrt2-1$

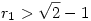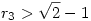Mivel $r_1>\sqrt2-1$ , ezért r₁>r₃ és $r_3>\sqrt2-1$ is teljül. Innen indukcióval nyerjük, hogy

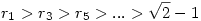$r_1>r_3>r_5>...>\sqrt2-1$ Teljesen hasonlóan

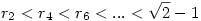
$r_2<r_4<r_6<...<\sqrt2-1$

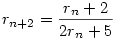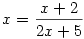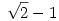A páratlan és páros indexű tagokból álló két sorozat külön külün szigorúan monoton és korlátos, tehát konvergens. Mivel $r_{n+2}=\frac{r_n+2}{2r_n+5}$ , ezért a hátérték mindkét esetben kielégíti az $x=\frac{x+2}{2x+5}$ egyenletet, aminek egyetlen pozitív megoldása a $\sqrt2-1$ . 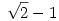Ha most "összefűzzük" a két sorozatot, akkor elég nagy n-től kezdve a páros és páratlan indexű elemek mindegyike elég közel lesz $\sqrt2-1$ -hez ( ez most nem precíz megfogalmazás!!), azaz az eredeti sorozatnak is ez a határértéke.

Előzmény: [427] Lóczi Lajos, 2005-11-09 11:26:20

[432] Ali	2005-11-09 15:10:08
Fordítva.
Előzmény: [431] Ali, 2005-11-09 15:08:33

[431] Ali	2005-11-09 15:08:33
Úgy van :-) A páratlan indexű szigorúan monoton növekvő, a páros indexű szigorúan monoton csökkenő. Találkoznak $\sqrt2-1$ -nél.
Előzmény: [430] Káli gúla, 2005-11-09 14:54:54

[430] Káli gúla	2005-11-09 14:54:54
"Melyik sorozat monoton?" Mind a kettő :)
Előzmény: [429] Ali, 2005-11-09 14:46:56

[429] Ali

2005-11-09 14:46:56

Melyik sorozat monoton ? Csak nem az r_n ?

$r_{2k-1} > \sqrt 2-1$ ; $r_{2k} < \sqrt 2-1$ , ahol k>0 egész.

Érdekelne az egyszerűbb megoldásod.

Előzmény: [425] Lóczi Lajos, 2005-11-09 02:28:48

[428] Gubbubu

2005-11-09 13:46:47

Egy tényleg egyszerűke kis feladat, kisebbeknek (a "szultán és rabok" néven is ismert fa. egy variációja):

Gilgames, Uruk város pateszije (uralkodója), a Legyőzhetetlen Bika, Az Istenek Ereje, Istár Istenasszony Kegyeltje, Győzedelmes Minden Égtájak Seregei Fölött, Kedves Az Égiek Előtt. etc. etc. trónra kerülése után az ilyen alkalmakkor szokásos közkegyelemben részesíti a Borzalmak Háza (az uruki börtön) nyomorult lakóit. Megbízza száz hű emberét, hogy az első mindegyik ajtót nyissa ki, a második minden másodikat zárja be, a harmadik minden harmadikat nyissson ki, a negyedik minden negyediket zárja be ... és így tovább. Mely sorszámú cellák rabjai szabadulnak?

[427] Lóczi Lajos	2005-11-09 11:26:20
Jó, nyilván arra vonatkozott a kérdés, hogy minél kisebb apparátussal hogyan bizonyítható az állítás; vagy hol nézhet utána az érdeklődő az idézett tételnek :)
Előzmény: [426] ágica, 2005-11-09 06:18:00

[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39]

Már regisztráltál?
Új vendég vagy?