| [661] Róbert Gida | 2011-09-24 19:14:02 |
 Aha, akkor q=2 (azaz 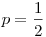 ) a megoldás. Hiszen először legyen ) a megoldás. Hiszen először legyen 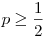 , vagy nem marad sárkányfiú egy hadjárat után, így nincs születés, és a kolónia kihal egy mértani sor szerint. Ha van sárkányfiú, akkor a hadjárat után legfeljebb , vagy nem marad sárkányfiú egy hadjárat után, így nincs születés, és a kolónia kihal egy mértani sor szerint. Ha van sárkányfiú, akkor a hadjárat után legfeljebb 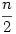 sárkány marad, (legalább) egyikük sárkányfiú, így legfeljebb sárkány marad, (legalább) egyikük sárkányfiú, így legfeljebb 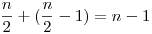 -en lesznek a hadjárat és a szülések után. Így n év alatt kihalnak. -en lesznek a hadjárat és a szülések után. Így n év alatt kihalnak.
Ha 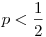 , akkor adható olyan n, amelyre a kolónia létszáma egy r>1 kvóciensű mértani sorozattal becsülhető alulról, így nem hal ki. (kezdetben egy sárkányfiú legyen a kolóniában, őt egy hadjárat során se öljék meg, és mindig sárkánylány szülessen.) , akkor adható olyan n, amelyre a kolónia létszáma egy r>1 kvóciensű mértani sorozattal becsülhető alulról, így nem hal ki. (kezdetben egy sárkányfiú legyen a kolóniában, őt egy hadjárat során se öljék meg, és mindig sárkánylány szülessen.)
|
| Előzmény: [660] Csimby, 2011-09-24 17:03:01 |
|
| [660] Csimby | 2011-09-24 17:03:01 |
 n-sárkányból legfeljebb 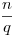 felsőegészrésznyit tud megölni. És a legnagyobb olyan q-t keressük amivel végezni tud velük. (Örök élet = végelgyengülésben nem hal meg. De ha levágják a fejét, akkor persze igen.) felsőegészrésznyit tud megölni. És a legnagyobb olyan q-t keressük amivel végezni tud velük. (Örök élet = végelgyengülésben nem hal meg. De ha levágják a fejét, akkor persze igen.)
|
| Előzmény: [658] Róbert Gida, 2011-09-24 10:56:30 |
|
|
| [658] Róbert Gida | 2011-09-24 10:56:30 |
 "Nyilván olyan p kell ami a "legrosszabb esetben" is működik." Nem nyilvánvaló.
"Példádban, ha örök életűek a sárkányfiúk akkor nem jó a p=0, mert Artúr egyet se öl meg, ők meg nem döglenek meg maguktól" De, akkor p>0 esetben egy örök életű sárkányt hogyan lehet megölni? Mert akkor az a sárkány nem örök életű.
Feladatodnak akkor viszont nincs megoldása: tegyük fel n>1 a kolónia létszáma kezdetben. Ha ennek p-ed részét ölik meg, akkor 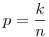 (0 (0 k k n egész), mivel ennek minden n>1-re müködnie kell így csak p=0 és p=1 lehet. De az előbbi nem megoldás szerinted. Míg p=1 sem lehet, mert: "p-ed részét sikerül legyilkolnia mielőtt felébrednek és elkergetik.", de akkor egy sárkány sem marad, így nem kergethette el őket senki. n egész), mivel ennek minden n>1-re müködnie kell így csak p=0 és p=1 lehet. De az előbbi nem megoldás szerinted. Míg p=1 sem lehet, mert: "p-ed részét sikerül legyilkolnia mielőtt felébrednek és elkergetik.", de akkor egy sárkány sem marad, így nem kergethette el őket senki.
|
|
| [657] Csimby | 2011-09-24 00:02:38 |
 Példádban, ha örök életűek a sárkányfiúk akkor nem jó a p=0, mert Artúr egyet se öl meg, ők meg nem döglenek meg maguktól. Nyilván olyan p kell ami a "legrosszabb esetben" is működik.
|
| Előzmény: [656] Róbert Gida, 2011-09-23 20:26:08 |
|
|
| [655] Csimby | 2011-09-23 18:52:48 |
 Artúr király minden télen hadjáratot indít a hegyekben élő sárkányok ellen, akik ilyenkor téli álmunkat alusszák barlangjukban. A barlangban talált jószágok p-ed részét sikerül legyilkolnia mielőtt felébrednek és elkergetik. Párzási időszak után minden sárkánylány kis sárkánynak ad életet (egészen addig amíg a kolóniában van fiú sárkány). A kis sárkányok, hála a mágikus környezetnek, már a következő párzási időszakra nemzőképesek lesznek. Mi a legkisebb p, amilyen hatékonysággal Artúr ki tudja irtani a sárkány kolóniát?
|
|
| [654] jonas | 2011-09-06 21:09:49 |
 A következő feladatot sokat ismerhetitek. Nem emlékszem, szerepelt-e már a fórumon.
Lássuk be, hogy a következő sorozat tagjai páronként relatív prímek.
3,5,17,257,65537,4294967297,...,22n+1,...
|
|
| [653] Valezius | 2011-04-12 14:38:15 |
 Egy 2nx2n méretű négyzetrácsos ábrába hurkot rajzolunk olyan módon, hogy a hurok minden négyzeten átmegy, és mindig oldalasan szomszédos mezők középpontjait köti össze. (Egyszerűbben mondva csak vízszintesen és függőlegesen mehetünk)
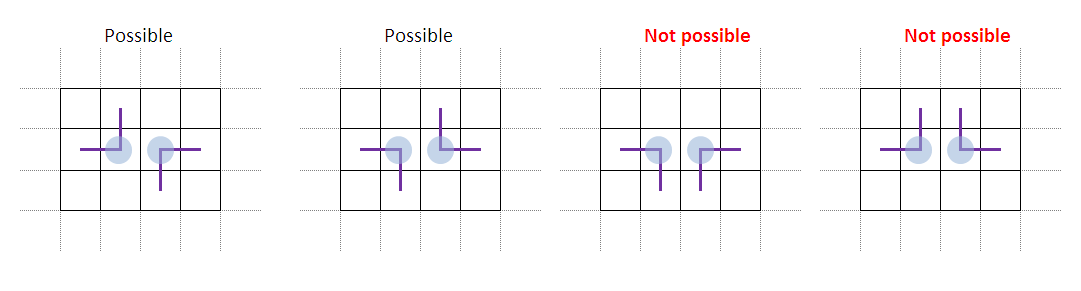
Az egyik helyre, ahol a hurok irányt vált (például az egyik sarokba) rajzolunk egy kört, majd a hurkon végighaladva minden második töréspontra (és csak azokra) újabb kört rajzolunk.
1. Lássuk be, hogy a 4 sarok közül pontosan két szemben lévőben lesz kör.
2. Ha két kör egymás mellett van, akkor a képen látható négy lehetőség közül csak az első kettő valósulhat meg.
Mindkét bizonyítást elég egyszerűnek gondolom, úgyhogy remélem jó helyen van az ujjgyakorlatok között.
A könnyebb érthetőség kedvéért itt van néhány logikai feladvány, ahol minden kör meg van adva, és a feladat a hurok megrajzolása. www.logikairejtveny.5mp.eu
|
 |
|
|
|
| [650] bily71 | 2010-09-01 21:36:23 |
 Legyen a=b+c !
Ekkor:
5a=5b+5c
4b+4c=4a
Adjuk össze a két egyenletet!
5a+4b+4c=5b+5c+4a
Mindkét oldalból vonjunk ki 9a-t!
4b+4c-4a=5b+5c-5a
Ebből:
4(b+c-a)=5(b+c-a)
Vagyis 4=5. Hol a hiba?
|
|
|
| [648] jenei.attila | 2010-08-31 16:00:59 |
 Ne haragudj Bily, de a kérdést nem átfogalmaztad, hanem egyszerűen mást kérdezel. A négyzetmentes számokra igaz, hogy nem hatványszámok, de fordídva nem. A kezdőtagok nevezőiben pedig as szerepel, akármi is az a. Tehát az eredeti kérdésedben, ahol azt mondtad hogy az a négyzetmentes, nem fog szerepelni a 12s, mivel a 12 nem négyzetmentes. Ha most azt mondod, hogy az a mégis inkább legyen nem hatványszám, akkor szerepelni fog benne, mivel a 12 valóban nem hatványszám. Előbb döntsd el hogy mit kérdezel, és ne tegyél úgy mintha én lennék értetlen hülye! Legalább annyit írhattál volna, hogy bocsi, rosszul tettem fel a kérdést. Még hogy átfogalmaztad... Most felbosszantottál.
|
| Előzmény: [646] bily71, 2010-08-31 14:23:52 |
|
| [647] SAMBUCA | 2010-08-31 15:24:20 |
 Egyszerűen megválaszolható, ujjgyakorlat :) két dolgot kell ellenőrízni:
a, minden 1/ns szerepel a jobboldalon
b, egyik sem szerepel kétszer.
Sambuca
|
| Előzmény: [646] bily71, 2010-08-31 14:23:52 |
|
| [646] bily71 | 2010-08-31 14:23:52 |
 Szerintem meg a kezdőtagok nevezőiben az a számok azok a pozitiv egészek, amelyek nem állnak elő a=br alakban, ahol b és r pozitiv egészek és r>1, azaz bármely 1-nél nagyobb r esetén a r-edik gyöke nem egész szám.
Az 1/12s úgy lesz kezdőtag, hogy nem szerepel egyik előző sorban sem, vagyis igy:
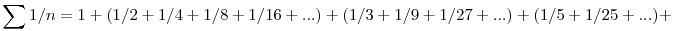
+(1/6+1/36+...)+(1/7+1/49+...)+(1/10+1/100+...)+(1/11+1/121+...)+(1/12+1/144+...)+...
Tehát a kérdésem átfogalmazva:
Igaz-e, hogy
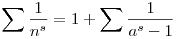
ahol a befutja a nem hatványszámokat, n pedig a pozitiv egészeket?
|
| Előzmény: [645] jenei.attila, 2010-08-31 08:53:06 |
|
| [645] jenei.attila | 2010-08-31 08:53:06 |
 Sajnos nem értem mire gondolsz: "csakhogy a kezdőtagok nevezőjében lévő a-k, mint ahogy az ellenpéldád is mutatja (az 1/12s is kezdőtag), nem azonosak a négyzetmentes számokkal"
Szerintem a kezdőtagok nevezői éppen a négyzetmentes számok. Továbbra sem találom az 1/12s-ent. Ez szerinted hogyan lesz kezdőtag? A következő hozzászólásodban az r mit jelent? Mi az, hogy az r-edik gyök nem egész szám? Létezik ilyen r, vagy minden r-re? Légyszíves próbáld ezt világosabban kifejteni. Köszi.
|
| Előzmény: [643] bily71, 2010-08-30 22:33:35 |
|
|
| [643] bily71 | 2010-08-30 22:33:35 |
 s=1 esetén:
1/1+1/2+1/3+...=1+(1/2+1/4+1/8...)+(1/3+1/9+1/27+...)+(1/5+1/25+1/125+)+...
s=2 esetén:
1/1+1/4+1/9+...=1+(1/4+1/16+1/64+...)+(1/9+1/81+1/729+...)+(1/25+1/625+1/15625+...)+...
...
A zárójelekben olyan mértani sorok vannak, melyek kezdőtagjai nem szerepeltek egyik elöző zárójelben sem és a kezdőtag egyenlő a kvócienssel, csakhogy a kezdőtagok nevezőjében lévő a-k, mint ahogy az ellenpéldád is mutatja (az 1/12s is kezdőtag), nem azonosak a négyzetmentes számokkal, ezen számok halmaza bővebb.
|
| Előzmény: [641] jenei.attila, 2010-08-30 12:23:13 |
|
|
|
|
|
|
| [637] bily71 | 2010-08-29 15:54:31 |
 Igaz-e, hogy
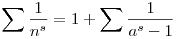
ahol s N, n végigfut a természetes számokon, a pedig az 1-nél nagyobb négyzetmentes számokon ? N, n végigfut a természetes számokon, a pedig az 1-nél nagyobb négyzetmentes számokon ?
|
|





 k
k






 N és r>1 esetén nem egész szám.
N és r>1 esetén nem egész szám.