| [110] Máté2 | 2004-02-22 21:59:03 |
 Megtudnátok oldani nekem ezt a feladatot Egy háromszög két kisebbik oldalát, a-t és b-t érintő hozzáírt körök sugarai ra és rb. A háromszög területe t=ra*rb. Mekkora a háromszög legnagyobb szöge?
|
|
| [109] lorantfy | 2004-02-10 08:18:20 |
 32. feladat: Oldjuk meg a valós számok halmazán:
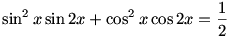
|
|
| [108] lorantfy | 2004-02-09 18:35:38 |
 Kedves Zormac!
Kösz a megoldást. A GEOMETRIA témában volt az említett feladat. Ha többet elárulok az ábráról akkor túl egyszerű lett volna, de Te jól értelmezted. Gratula!
|
 |
| Előzmény: [107] Zormac, 2004-02-09 17:04:03 |
|
| [107] Zormac | 2004-02-09 17:04:03 |
 (egyébként gondolom, ez a feladat valahogy abból a - szintén valahol errefelé előfordult - feladatból született, hogy feldarabolható-e egy kör olyan egybevágó alakzatokra, melyek között van olyan, amely nem tartalmazza a középpontot még a határán sem - de önmagában is szép :-)
|
| Előzmény: [106] Zormac, 2004-02-09 17:00:18 |
|
| [106] Zormac | 2004-02-09 17:00:18 |
 31. megoldás
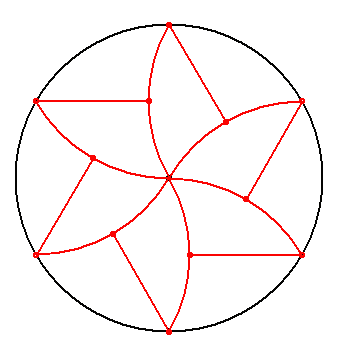
Remélem, jól értem az ábra szerkezetét...
Legyen a külső hat csúcs pozitív körüljárás szerint A, B, C, D, E, F. Akkor ABCDEF egy egységoldalú szabályos hatszög, amelynek területe legyen T6 (egyébként 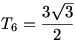 , de ez lényegtelen). A hatszög középpontja legyen O. , de ez lényegtelen). A hatszög középpontja legyen O.
Legyen mondjuk a B pontból induló kis körív másik végpontja B1 (amely rajta van az AC egyenesen, mégpedig C-hez közelebb). BB1C egy afféle "amorf konkáv" háromszög :-), amelynek t területére
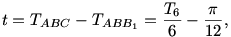
hiszen 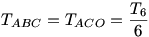 , másfelől TABB1 az egységsugarú kör 30 fokos cikke, tehát területe valóban , másfelől TABB1 az egységsugarú kör 30 fokos cikke, tehát területe valóban 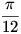 . Innen a keresett T területre . Innen a keresett T területre
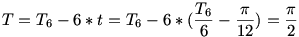
adódik. Jééé!
Ilyenkor szokott az ember gyanút fogni, hogy nem bonyolított-e el egy elegáns geometriafeladatot randa számolással? És tessék, hát dehogynem!
(Sajnos nincs a kezem ügyében egy rajzoló tool, így csak szövegesen mondom, mit kell látni :-)
Hosszabbítsuk meg az alakzat határát alkotó köríveket "befelé", egészen a középpontig (mert ugye az látható, hogy ott találkoznak). A fenti jelölésekkel élve ekkor BB1C és OB1C egybevágó síkidomok, melyeknek B1C oldala közös egyenes szakasz, másik két oldaluk pedig egységsugarú körív. E két egybevágó síkidom elforgatottjai együttesen a teljes kört kiadják s egy-egy egybevágó pár egyike "kint", másika "bent" van, tehát a kérdéses síkidom területe az egységsugarú kör területének fele, azaz valóban 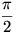 . .
z.
|
| Előzmény: [105] lorantfy, 2004-02-01 22:31:20 |
|
| [105] lorantfy | 2004-02-01 22:31:20 |
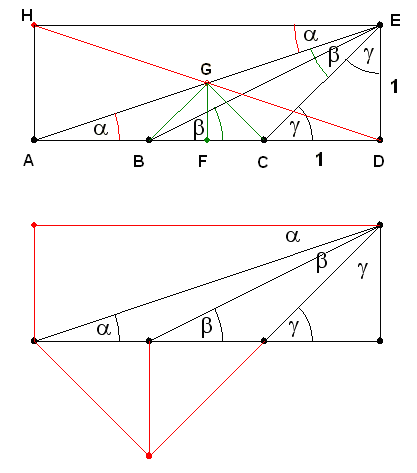
 31. feladat: Mekkora az alábbi egyenes szakaszokból és egységnyi sugarú körívekből álló síkidom területe?
|
 |
|
| [104] Gubbubu | 2004-01-29 21:47:43 |
 Kedves Csimby!
Mit is modnhatnék? Úgy látszik, a matematikának megvannak a maga Dr. Watsonai, akik ostoba és elhamarkodott kérdéseik és következtetéseik ellenére (esetleg) segítik ama Sherlock Holmesokat, akik éles elméjük és megfigyelőkészségük segítségével kibogozzák a rejtelmes ügyeket! Te pedig ez utóbbiak közé tartozol!
Az előbbi gondolatmenet nem jutott az eszembe annak ellenére, hogy Suhanc másik feladatát hasonló gondolatmenettel lehet megoldani (mentségemre szolgáljon, hogy még nem is nagyon volt időm gondolkozni a feladaton, csak kitűztem - az utóbbi időben nem matematikával, hanem különféle érdekes vírusprogramok, mint pl. a "Shimgapi-Mydoom.A", az "MSBLAST" és hasonlók blokkolásával és kiirtásával kell foglalatoskodnom, tegnap szinte egész délután és éjjel ezt csináltam, és csak közben írtam "unalmamban" egy-két hozzászólást ...)
Ám ha már megemlítettem, következzen itt a másik oszthatósági feladat megoldása:
"Suhanc 5." fa. megoldása:
Lássuk be, hogy 512 egész szám között van néhány darab, amelyek összege osztható 512-vel!
Ehelyett én belátom, hogy tetszőleges m pozitív egész számot választva ezek között van néhány, amelyek összege osztható m-mel (m=512 esetén adódik "Suhanc 5").
Legyenek számaink a1,a2,...,am  Z! Lehetnek köztük azonosak is, akár mind is azonosak. Tehát 512 db. nem feltétlenül különböző egész számról van szó. Z! Lehetnek köztük azonosak is, akár mind is azonosak. Tehát 512 db. nem feltétlenül különböző egész számról van szó.
Felírunk legalább m db., az ai elemekből mint tagokból álló összeget úgy, hogy az ilyen összegek különbsége is összeg legyen. A legegyszerűbb ilyen lehetőség m db. ilyen összeg felírására:
a1:=S1
a1+a2:=S2
a1+a2+a3:=S3
...
a1+a2+...+am:=Sm.
Két ilyen összeg különbsége is az ai tagokból álló összeg, Sj-Si=ai+1+ai+2+...+aj (j>i) Ha van olyan Si összeg, amelynek m osztója, készen vagyunk. Ellenben az m db. Si összeg maximum m-1-féle maradékot adhat mod(m). Ez az a szituáció és gondolatmenet, amellyel megoldottad az előző feladatot. A skatulya-elv alapján tehát valamely két összeg ugyanolyan maradékot ad mod(m), ami azt jelenti, hogy különbségük - ami maga is az ai számok valamely összege - 0 maradékot ad mod(m). Ismét csak kész vagyunk.
Adalék: Mindkét feladatban arról volt szó, hogy adott néhány (n) szám, ezek közül kiválasztható k db. (0<k<n+1), amely osztható valamely m számmal.
Érdekes lehet a következő "additív számelméleti" függvény: M(n,m) legyen az a legkisebb szám, melyre igaz, hogy ha n db. tetszőlegesen választott egész szám közül kiválasztunk ennyi, azaz M=k(n,m) darabot, akkor ezek összege (a megadott és a kiválasztott számok konkrét értékétől függetlenül, biztosan) osztható legyen m-mel.
Egy másik érdekes függvény, k(n,m) legyen az a legkisebb szám, amelyre igaz, hogy ennyi darab, egyéb tekintetben tetszőlegesen választott egész szám között biztosan legyen n db., melyek összege osztható m-mel (ez egyfajta Ramsey-szám, csak nem gráfokra, hanem számokra).
Egy nevezetes állítás az Erdős-Ginzburg-Ziv-tétel, amely szerint k(m,m)=2m-1. Azaz 2m-1 db. tetszőlegesen választott egész szám között már biztosan van m db., melyek összege osztható m-mel (de 2m-2 db. szám között már nem biztosan).
Üdv mindenkinek:G.
|
| Előzmény: [103] Csimby, 2004-01-29 13:35:52 |
|
| [103] Csimby | 2004-01-29 13:35:52 |
 Kedves Gubbubu!
Nem csak prímekre van végtelen sok megoldás. Legyen az osztó: q tetszőleges poz. egész, ekkor az f(n),f(n+1),f(n+2),...,f(n+q) számok között biztosan lesz legalább 2 amely q-val osztva ugyan annyi maradékot ad, hiszen q-val osztva q féle különböző maradékot kaphatunk ez viszont q+1 db. szám (skatulya elv). Ekkor azonban nem tudjuk pontosan megmondani, hogy melyik kettő ad ugyan annyi maradékot, csak azt tudjuk, hogy biztosan lesz 2 amely ugyanannyi maradékot ad.
|
|
| [102] Gubbubu | 2004-01-29 01:37:28 |
 Kedves Csimby!
Gratulálok! Ezt gyorsan összehoztad!
Ennek alapján tetszőleges p>5 prímre is létezik végtelen sok különböző n,k természetes szám úgy, hogy p|f(n)-f(k) legyen.
Sőt, ha A>1 tetszőleges szám, akkor bármely p>A prímhez (ekkor biztosan (A,p)=(d,p)=1 , A minden d osztójára), létezik végtelen sok olyan különböző n,k természetes szám, hogy
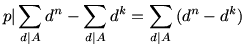
teljesüljön. Szerintem ezt már nem lenne olyan egyszerű belátni, ha valaki nem ismerné az előzményeket....
|
| Előzmény: [101] Csimby, 2004-01-28 22:58:26 |
|
| [101] Csimby | 2004-01-28 22:58:26 |
 30.feladat
1237prím a1236 a1236 1 1
f(n+1236)=2n+1236+3n+1236+5n+1236 2n+3n+5n=f(n). 2n+3n+5n=f(n).
Tehát f(n) és f(n+1236) ugyan annyi maradékot ad 1237-tel osztva, tehát tényleg végtelen sok megoldás van!
|
|
| [100] Csimby | 2004-01-28 22:20:18 |
 A 30. feladathoz Ha n,k <100 akkor a következő n,k számpárok jók: (94,12) (63,25) (96,27)
1000-ig 419 db megfelelő számpár van, 2000-ig 2377 db, 3000-ig 5966 db, 4000-ig 11153 db, A sejtés tehát az, hogy végtelen sok megoldás van.
|
|
| [99] Gubbubu | 2004-01-28 21:47:45 |
 Kedves Csimby!
Közben rájöttem én is, hogy szokásom szerint elhamarkodtam a dolgot! Rossz az egész! Hiába, öregszem... bocs!
Rajzolgattam egy pár grafikont, és rájöttem, hogy a feladat nehezebb, mint gondoltam!
Tehát, bár a "Suhanc 4." feladat megoldott, de adott helyette a a következő (amit most nem tudok, hogy ujjgyakorlat-e):
30. feladat:
Igazoljuk, hogy f(n):=2n+3n+5n esetén nincsenek olyan különböző n,k N számok, melyekre 1237|f(n)-f(k) (vagy igazoljuk az ellenkezőjét...)! N számok, melyekre 1237|f(n)-f(k) (vagy igazoljuk az ellenkezőjét...)!
Azt hiszem, egyébként az általam készített táblázat nem is igen fog segíteni a megoldásban. De nem baj, olyan szépen mutat, és ez az első TeX-ben készített táblázatom...
Üdv mindenkinek: G. Most pedig megyek, napolajat teszek a képemre...
|
| Előzmény: [98] Csimby, 2004-01-28 21:15:41 |
|
| [98] Csimby | 2004-01-28 21:15:41 |
 Kedves Gubbubu: Nem csak a 7-re végződő számok oszthatóak 1237-tel, te is írtad az n=k esetet ahol a különbség 0 (nem 7-re végződik, de megfelel).
"Vagyis 1237 csak úgy lehet f(n)-f(k), ha f(k)=3. " Nem csak 1237 lehet a különbség, hanem k*1237.
De az is lehet, hogy valamit félreértettem...
|
|
| [97] Gubbubu | 2004-01-28 19:07:29 |
 Kedves Fórum!
Megoldást küldöm Suhanc első "elfeledett" feladataira:
"Suhanc 4." fa. megoldása:
Természetesen 1237|(2n+3n+5n)-(2k+3k+5k)=0 bármely n,k N,n=k-ra. Lehet pl. n=2. N,n=k-ra. Lehet pl. n=2.
Na jó, ez így túl könnyű volt. Kössük ki, hogy n>k (ez az általánosság megszorítása nélkül kiköthető, az n<k esetben ugyanis a hatványösszegek különbségei egymás ellentettjei lesznek, így az n>k párra ennek épp akkor osztója bármi, még az 1237 is, ha az n<k osztója.
Legyen f(n):=2n+3n+5n, és tekintsük a következő táblázatot, mely oszlopai sorra n-t, 2n-t mod 10, 3n-t mod 10, 5n-t mod 10, végül f(n)-t mod 10 tartalmazzák (vagyis e mennyiségek utolsó számjegyét:
| n |
2n |
3n |
5n |
f(n) |
| 0 |
1 |
1 |
1 |
3 |
| 1 |
2 |
3 |
5 |
0 |
| 2 |
4 |
9 |
5 |
8 |
| 3 |
8 |
7 |
5 |
0 |
| 4 |
6 |
1 |
5 |
2 |
| 5 |
2 |
3 |
5 |
0 |
| 6 |
4 |
9 |
5 |
8 |
| ... |
... |
... |
... |
... |
|
Látható, de könnyen be is látható (akár kongruenciákkal számolva, akár a tízes számrendszerben számjegyeket szorozgatva), hogy a táblázat periodikus, az n=1-től kezdve a 4 legkisebb periódussal.
Tehát f(n)-f(k) mod(10) számolva a 3-0=3, 3-8=-5=5, 3-2=1, 0-3=7, 0-0=0, 0-8=2, 0-2=8, 8-3=5, 8-0=8, 8-8=0, 8-2=6, 2-3=9, 2-0=2, 2-8=4, 2-2=0 értékeket veheti fel. A fenti felsorolásból láthatóan nem sokszor kapunk 7-et, úgy lehet csak f(n)-f(k) 7 mod(10), ha k=1. Vagyis 1237 csak úgy lehet f(n)-f(k), ha f(k)=3.
1237=f(n)-3;
1240=f(n); Ez az egyenlet pedig nem megoldható. n=5 már túl sok (több mint 3000 f(n) értéke, mivel 55=3125, n=4 pedig túl kevés, f(n)=722. Vagyis ha n és k különbözőek, akkor nincs megoldás. Az egyetlen megoldás n=k.
Nemsokára felteszem a másik "elfeledett" feladat megoldását is. G.
|
| Előzmény: [92] Suhanc, 2004-01-24 10:05:31 |
|
|
|
|
| [93] lorantfy | 2004-01-24 11:11:26 |
 Kedves Fórumosok
Valóban Suhanc 4. és 5. feladata feledésbe merült. Ebben én is hibás vagyok, mert véletlenül felülszámoztam.
A megoldatlan feladatok listája ebben a témában:
4. 5. [6]
6. [18]
13. [48]
16 [53]
18.b [69]
22. [77]
24. [81]
27. [86]
29. [92]
Kérek minden feladatkitűzőt, hogy feladatát (lehetőleg félkövér kiemeléssel) számozza és a megoldókat pedig arra, hogy hivatkozzanak a feladatszámra! Köszönettel: L.
|
| Előzmény: [90] Gubbubu, 2004-01-24 09:04:36 |
|
| [92] Suhanc | 2004-01-24 10:05:31 |
 Kedves Gubbubu!
De, tényleg ez volt a feladat...odaírtam mellé, hogy ez villámkérdés...igazából annak is elég rövidke...:)
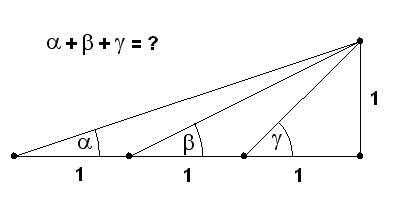
Ezen a szakörön legutóbb találkoztam egy egyszerű, de nagyon aranyos feladattal; "ohne nehézség" felkiáltással leírom:
29. feladat
Legyenek a;b;c egy háromszög oldalai! Igazoljuk, hogy
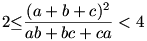
|
| Előzmény: [90] Gubbubu, 2004-01-24 09:04:36 |
|
| [91] Suhanc | 2004-01-24 09:42:13 |
 Kedves László!
Hát Igen! Ez valóban pár sorral rövidebb...;) Köszönöm!!:) Én általában szeretem az olyan geometriai feladatokat, amikről időközben kiderül, hgy lényegében nem is geometria... de azért túlzásokba nem szabad esni!!!;)
|
|
| [90] Gubbubu | 2004-01-24 09:04:36 |
 Kedves Suhanc!
[6] hozzászólásodban szerepel két, azóta "elfeledett", pedig elég érdekes feladat. A második főként trükkös és jópofa, de az elsőt nem egészen értem. "Tekintve 2,3,5 n-edik hatványainak összegét, van két szám, amelynek különbsége osztható 1237-tel". Gondolom, nem arról van szó, hogy keressünk olyan n,k számokat, melyekre 1237|(2n+3n+5n)-(2k+3k+5k), mivel ez még ujjgyakorlatnak is túl egyszerű lenne. Miről van szó pontosabban?
Üdv: G.
|
| Előzmény: [6] Suhanc, 2003-11-26 18:24:56 |
|
|
| [88] Suhanc | 2004-01-23 22:46:07 |
 Kedves Károly!
A feladatodra van egy megoldásom, de eléggé ronda (ágyúval galambra...) ha nem kerül föl más megoldás, feltennéd a tiédet? (azt is megköszönöm, ha mailben elküldöd).
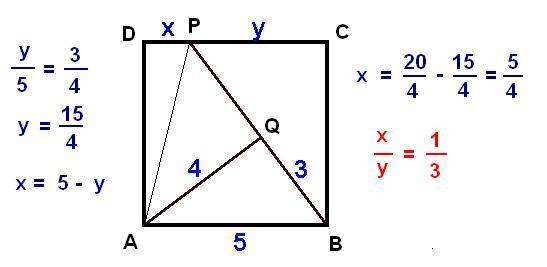
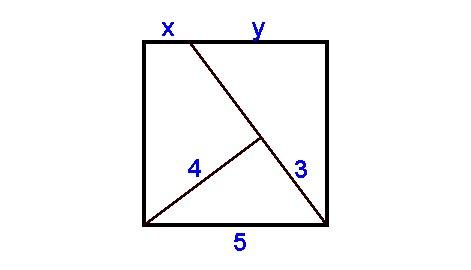
M: (sajnos, az ábraszerkesztéssel nem vagyok megbarátkozva) Legyenek a négyzet csúcsai A;B;C;D pontok, úgy, hogy A legyen az ábra bal alsó sarkában (óramutató járásaval ellentétesen betűzve). x és y szakaszok közös pontja legyen P, a 3 és 4 egységnyi szakaszok közös pontja legyen Q.
ADP és APQ háromszögek derékszögűek; a Pitagorasz-tétel szerint: 25+x2=z2+16
Ebből: 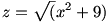
PBC derékszögű háromszögre felírva a Pitagorasz-tételt: 
Négyzetre emelve: 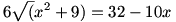
Tovább bontogatva a 16x2-160x+175=0 egyenletet kapjuk, melynek megoldásai X1=35/4;eznyilvánnemmegoldás,mertX<5;ésX2=5/4. Ekkor y=15/4 , tehát x/y=1/3 .
|
|
| [87] Hajba Károly | 2004-01-20 09:45:35 |
 Egy kis szösszenet
28. feladat:
Mennyi x:y aránya az 5*5 négyzet esetén?
|
 |
|
|








 Z! Lehetnek köztük azonosak is, akár mind is azonosak. Tehát 512 db. nem feltétlenül különböző egész számról van szó.
Z! Lehetnek köztük azonosak is, akár mind is azonosak. Tehát 512 db. nem feltétlenül különböző egész számról van szó. 
 a1236
a1236 1
1 -nek CGF
-nek CGF =
= .
. 

 +
+ a külsőszög-tétel miatt. Tehát a keresett öszzeg 2
a külsőszög-tétel miatt. Tehát a keresett öszzeg 2