|
| [1160] huu | 2013-03-11 05:54:09 |
 Üdv!
lenne egy feladatom. Kérlek segítsetek a megoldásában. Előre is köszönöm.
Egy vasúti kocsi belsejében, a tetőre függesztenek egy 0.8 kg tömegű testet egy nyújthatatlan és elhanyagolható tömegű kötélre. A vasúti kocsi állandó 2.2 m/s2 gyorsulással gyorsít. Mekkora szöget (fokban) zár be a kötél a függőlegessel?
|
|
|
| [1156] Sára88 | 2012-12-14 13:35:23 |
 Köszönöm szépen a segítséged! A hibaterjedési törvény képletének az alkalmazásával kell a hibát becsülni, ez a feladat lényege. de remélem el tudom kezdeni a segítségeddel! Köszi a válaszod még egyszer!
|
| Előzmény: [1155] Gézoo, 2012-12-14 13:05:48 |
|
| [1155] Gézoo | 2012-12-14 13:05:48 |
 I=4,5/3000=1,5 mA
A digi műszerek 4 jegy +- 1 digit Ez a feszültség méréskor +-10 mV hibát okoz, a 19,99V-os méréshatárnál, áram méréskor 1,999 mA méréshatárnál +-1uA hibát
Az analóg tükrös-nagyítós műszerek leolvashatósága +-0,5
neked +-3 Ohm pontosság kell, akkor a hiba nem lehet nagyobb mint +-0,1
Az eredményt hányados adja azaz a legnagyobb hiba nagysága határozza meg a mérés hibáját.
a 4500 mV-nak a 10 mV 1/450-ed része 0,2
Így, vagy etalonnal kalibrált híd kapcsolást kellene használni, vagy ami ezzel egyenértékű, etalonnal felépített kalibrált feszültség generátort és az 1,999 mA -es méréshatárt használva áramot mérni.
Persze lehet, hogy a feladatnak más a célja. Akkor teljesen más is lehet a megoldás.
|
| Előzmény: [1154] Sára88, 2012-12-14 12:26:13 |
|
| [1154] Sára88 | 2012-12-14 12:26:13 |
 Sziasztok! Valaki tudna nekem segíteni ebben a feladatban???
Egy termisztor ellenállását Ohm törvénye alapján, a rá eső feszültség (Ux) és a rajta folyó áram (Ix) mérésével akarjuk meghatározni: Rx=Ux/Ix A termisztorra kapcsolt feszültség kb. 4,5 V, a termisztor ellenállása a kérdéses tartományban kb. 3 kOhm. A méréshez egy digitális multimétert (méréshatárok feszültségmérésre 0.1999 V, 1.999 V és 19.99 V, árammérésre 1.999 mA, 19.99 mA, 199.9 mA és 1.999 A, a pontosság minden esetben ±1 digit) és egy analóg multimétert (méréshatárok feszültségmérésre 0.6 V, 1.2 V, 3 V, 12 V és 30 V, árammérésre 1.2 mA, 3 mA, 12 mA, 30 mA és 120 mA, a pontosság minden esetben a méréshatár ± 0.5 Milyen összeállításban érjük el a nagyobb pontosságot Rx meghatározásában, mekkora így Rx hibája? + Ha feszültségmérésre a fenti digitális multimétert használjuk, milyen pontosságú árammérővel lehetne elérni a ±3 Ohmos pontosságot?
|
|
| [1153] lorantfy | 2012-12-03 16:24:27 |
 Tartok tőle, hogy Robinak ez túl nagy ugrás. Első lépésként talán kilogikázhatnád Robi, hogy ha 10 N 20 cm-es megnyúlást okoz egy gumin, akkor 5 cm-es megnyújtáshoz mekkora erő kell két gumi esetén. Azután már kiszámolhatod, mekkora munkát végzünk a gumik megnyújtásakor. Ez pedig választ ad Mihály előző kérdésére. Abból pedig már megkapod a sebességet.
|
| Előzmény: [1152] Fálesz Mihály, 2012-12-03 11:36:57 |
|
|
| [1151] Robi01 | 2012-12-02 21:58:25 |
 Kérlek segítsen valaki! Lenne itt 1 feladat ami egy kicsit kifogott rajtam és ha valaki tudja a megoldást annak nagyon hálás lennék! :)
Tehát: Csúzlit készítünk két olyan hosszú gumiszalagból, amelyeket 10N erő külön-külön 20cm-rel nyújt meg. A csúzlit 5cm-rel kihúzva mekkora kezdősebességet adhatunk az 50g tömegű kavicsnak? ( A veszteségtől eltekintünk. )
előre is köszönöm a segítséget ;-)
|
|
| [1150] Syac | 2012-11-03 20:39:41 |
 Kedves Hozzászólók!
Köszönöm a véleményeket és a megoldásokat!
Üdv.!
|
|
|
| [1148] Geg | 2012-11-02 06:42:25 |
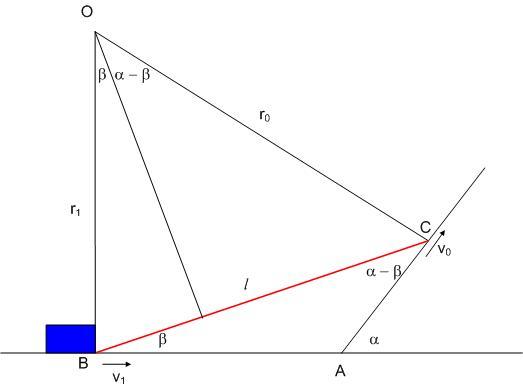
 Talan egy kicsit egyszerubb megoldas (bar izles dolga) nem pillanatnyi forgastengellyel szamolni, hanem kihasznalni, hogy a mozgas leirhato a tomegkozeppont halado es akoruli forgassal is.
A lenyeg az, hogy (hasznalva az elozo abra jeloleseit) ha mind a C, mind a B pontok sebessegebol kivonjuk a csak a forgasbol szarmazo sebessegjarulekot, akkor ugyanazt, nevezetesen a tkp. sebesseget kell, hogy megkapjuk.
A C es B pontok sebessege:
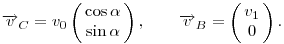
A csak a forgasbol szarmazo jarulekok a C es B pontokban:
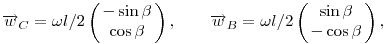
ahol  a szogsebesseg. A tkp. sebessege ketfelekepp kifejezve: a szogsebesseg. A tkp. sebessege ketfelekepp kifejezve:
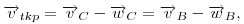
amely egyenlet x es y komponensebol kapjuk rendre, hogy:
v1=v0cos  + + lsin lsin  , ,
v0sin  = = lcos lcos  . .
A masodik egyenletbol kifejezve  -t, majd beirva az elsobe kapjuk, hogy: -t, majd beirva az elsobe kapjuk, hogy:
v1=v0cos  +v0sin +v0sin  tg tg  . .
Kihasznalva, hogy   / / t= t= , a B pont gyorsulasara kapjuk, hogy: , a B pont gyorsulasara kapjuk, hogy:
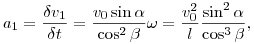
vagyis a keresett ero:
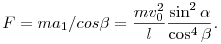
|
|
| [1147] HoA | 2012-11-01 09:01:13 |
 Megvan a hiányzó cos( ) ! Ugyanis a kötélerő és a szánkó gyorsulásának iránya nem azonos. A szánkó gyorsuéását a kötélerő vízszintes összetevője okozza. A gyorsulás ( a ) valóban a fenti. Viszont a kötélerőre ) ! Ugyanis a kötélerő és a szánkó gyorsulásának iránya nem azonos. A szánkó gyorsuéását a kötélerő vízszintes összetevője okozza. A gyorsulás ( a ) valóban a fenti. Viszont a kötélerőre
K.cos( )=m.a )=m.a
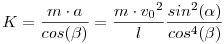
|
| Előzmény: [1146] HoA, 2012-10-31 21:29:39 |
|
|
| [1145] HoA | 2012-10-29 23:45:26 |
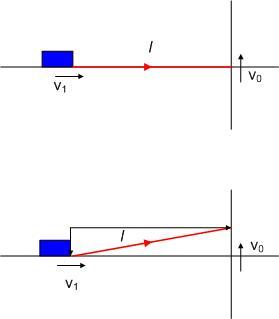
 A képlet elfogadhatóságának alátámasztására vizsgáljunk egy speciális esetet. Legyen  =90o, =90o, =0o , vagyis a kötél szabad végét húzzuk egy függőleges fal mentén és tekintsük azt a pillanatot , amikor a kötél éppen vizszintes. A kötél szabad végének sebessége v0 , a szánkóé v1=0 . =0o , vagyis a kötél szabad végét húzzuk egy függőleges fal mentén és tekintsük azt a pillanatot , amikor a kötél éppen vizszintes. A kötél szabad végének sebessége v0 , a szánkóé v1=0 .  t idő múltán a szabad vég elmozdulása v0 t idő múltán a szabad vég elmozdulása v0 t . A feszes kötél merev rúdnak tekinthető. A pillanatnyi forgástengelyt a végpontok sebességének irányára emelt merőlegesek metszéspontjaként szerkesztve a végpontok forgástengelytől mért távolságai: r0 l-nek vehető, r1=v0 t . A feszes kötél merev rúdnak tekinthető. A pillanatnyi forgástengelyt a végpontok sebességének irányára emelt merőlegesek metszéspontjaként szerkesztve a végpontok forgástengelytől mért távolságai: r0 l-nek vehető, r1=v0 t , v1= t , v1= v1 , a sebességek a forgástengelytől mért távolsággal arányosak : v1 , a sebességek a forgástengelytől mért távolsággal arányosak : 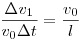 . A gyorsulás . A gyorsulás 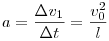 . A kötélerő ennek m-szerese, összhangban a képlettel , hiszen esetünkben a szereplő szögfüggvény hányados 1/1. . A kötélerő ennek m-szerese, összhangban a képlettel , hiszen esetünkben a szereplő szögfüggvény hányados 1/1.
A megközelítés általános  és és esetében is alkalmazható, csak a pillanatnyi forgástengelytől mért távolságok és ebből v1 változásának számítása bonyolultabb. esetében is alkalmazható, csak a pillanatnyi forgástengelytől mért távolságok és ebből v1 változásának számítása bonyolultabb.
|
 |
| Előzmény: [1144] Syac, 2012-10-29 20:45:14 |
|
| [1144] Syac | 2012-10-29 20:45:14 |
 Köszönöm az eddigi válaszokat. Egyetértek mindkét hozzászólóval. A feladat megoldása mégis:
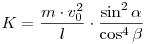
Várom a további ötleteket (lehet, hogy a feladat szövege hibás?).
Köszönöm!
|
|
|
|
| [1141] Syac | 2012-10-27 08:57:32 |
 Kedves Fizikások!
Az alábbi feladat megoldásához kérnék segítséget:
Egy ember az  hajlásszögű lejtőn állandó v0 sebességgel felfelé haladva elhanyagolható tömegű, l hosszúságú kötél segítségével m tömegű szánkót húz maga után úgy, hogy a szánkó még vízszintesen mozog. A kötél a vízszintessel hajlásszögű lejtőn állandó v0 sebességgel felfelé haladva elhanyagolható tömegű, l hosszúságú kötél segítségével m tömegű szánkót húz maga után úgy, hogy a szánkó még vízszintesen mozog. A kötél a vízszintessel  szöget zár be. Hogyan függ a fellépő kötélerő a szöget zár be. Hogyan függ a fellépő kötélerő a  szögtől? (A szánkó és a felület közötti súrlódás elhanyagolható.) szögtől? (A szánkó és a felület közötti súrlódás elhanyagolható.)
Köszönöm!
|
|
| [1140] gyg | 2012-10-25 20:06:04 |
 Mindegy, melyiket vesszük állónak. Ha a bal pedál áll, akkor a tengelye, ami balos csavarmenettel van rögzítve a hajtókarhoz, a hajtókar felől nézve óramutató járásával megegyező, tehát a menetet lazító irányba forog. Időközben utánanéztem és egy angol nyelvű forrás a precesszióval magyarázza azt, miért kell a bal pedálra balos menet, igaz, nem írja le precízen. Ha jól értem, a tengely apró mozgása, amennyit a csavarmenet enged, okoz forgatónyomatékot ami nagyobb, mint a csapágy súrlódása miatt keletkező oldó irányú forgatónyomaték és ezért nem tekeredik ki. Ha a csapágy súrlódása rendellenesen megnő, (nem forog a pedál) akkor a hajtástól az ki fog tekeredni.
|
| Előzmény: [1139] stony13, 2012-10-24 21:21:19 |
|
| [1139] stony13 | 2012-10-24 21:21:19 |
 Próbáld úgy elképzelni, hogy nem a pedált csavarod bele a hajtókarba, hanem fordítva, a hajtókart a rögzített pedálba (tulajdonképpen ez történik biciklizés közben is, mert a pedált a talpaddal megközelítőleg vízszintes helyzetben tartod folyamatosan). Milyen irányba kellene forgatni a hajtókart?
|
| Előzmény: [1138] gyg, 2012-10-24 20:14:26 |
|
| [1138] gyg | 2012-10-24 20:14:26 |
 Sziasztok. Meg tudná valaki közérthetően és pontosan magyarázni, miért van a kerékpár bal pedálján balmenet, a jobbon jobbmenet? Nyilván azért, mert így nem tekeredik ki üzem közben, de ha csak a pedál és a hajtókar közti tengelyt figyeljük, ahol az említett bal és jobbmenettel csatlakoznak, ott pont a kitekeredő irányba forognak egymáshoz képest. Hogy van ez?
|
|
| [1137] gildike | 2012-10-16 13:58:13 |
 köszönöm mindenkinek a segítséget remélem legalább a 2 est összetudom hozni.
|
|
| [1136] Gézoo | 2012-10-16 12:22:25 |
 1. Sajnos nem tudom, azt a mentősöktől kellene megtudni, hogy melyik frekvenciát használják.
2. A sok jelentés közül a kérdésed az autótranszformátor régi elnevezését idézi. Tilos olyan helyeken alkalmazni ahol teljes leválasztás az előírás. A leggyakoribb alkalmazási területe a gépjárművek gyújtótrafói.
3. Két módon juthat be. Az egyik a vezetékkel érintkező felületen, a másik a kapacitív csatolás, ahol a testfelszín mint kondenzátor fegyverzete vesz részt a folyamatban.
4. Több elterjed módszere van. Többek között a kapacitív-szaggatós (sokszorozós) elven és a piezo -"transzformátorok" alkalmazásával. Mindkét említett módszer egyenfeszültséget váltófesz képzése nélkül közvetlenül alakít más nagyságú egyenfesszé.
5. Első az, hogy szigetelő eszköz segítségével megszakítsuk az áramkört. Friss levegőn, nyugalomba kell helyezni a sérültet és mentőt kell hívni hozzá. TILOS! Folyadékot itatni vele! 6. U2/N2 = U1/N1 Azaz U2=400 V N2=1200 N1=600 akkor U1= N1*U2/N2
7. Mint 6-os feladatban, de a vasveszteséget célszerű hozzáadni.
|
| Előzmény: [1133] gildike, 2012-10-15 20:01:17 |
|
| [1135] gildike | 2012-10-16 12:13:38 |
 sajnos ez a főiskola, a tanár leadott egy bizonyos anyagot erre zh ban meg olyat kérdez ami benne sincs a diákba. számítást egyáltalán nem is vettünk.
|
|






 a szogsebesseg. A tkp. sebessege ketfelekepp kifejezve:
a szogsebesseg. A tkp. sebessege ketfelekepp kifejezve:  +
+ ,
,

 t idő múltán a szabad vég elmozdulása v0
t idő múltán a szabad vég elmozdulása v0


