| [294] jonas | 2010-02-23 11:17:15 |
 Hogyha az egyik huzal sokkal vékonyabb, mint a másik, akkor a vastag huzalban hengerszimmetrikus az áramsűrűség?
Ha igen, akkor mitől változna ez meg, ha a másik vezeték is vastagabb lesz? Hiszen ha az első vezeték vékonyról vastagra változik, de továbbra is hengerszimmetrikusan folyik benne az áram, ezért ugyanolyan elektromágneses teret csinál, mint ha vékony lenne, akkor a másik vezeték nem veheti észre, hogy az egyik vastag vagy vékony, tehát ha a másikat is vastagra változtatod, akkor abban is hengerszimmetrikusan folyik az áram, és ugyanolyan erővel kell vonzaniuk egymást, mint két vékony vezetéknek.
Ha viszont nem hengerszimmetrikus az áram, akkor miért lesz mégis ugyanaz a két vezeték közti erő függetlenül a vastag vezeték átmérőjétől?
|
| Előzmény: [293] Geg, 2010-02-23 10:47:13 |
|
| [293] Geg | 2010-02-23 10:47:13 |
 Valoban nem szukseges, hogy a huzal atmeroje elhanyagolhato legyen. Ugyanis Ampere torvenye szerint
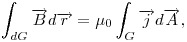
ahol a bal oldalon egy zart gorbe menten kell integralni a magneses indukcio vektorat, jobb oldalon pedig a gorbe altal kijelolt feluletre kell integralni az aramsuruseget. Legyen a szoban forgo gorbe egy kor, melynek kozeppontja atmegy a huzal kozeppontjan. Hengerszimmetriat feltetelezve a bal oldal B×2R , ahol R a korunk sugara. Szemmel lathatoan ekkor fuggetlenul attol, hogy a , ahol R a korunk sugara. Szemmel lathatoan ekkor fuggetlenul attol, hogy a 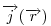 fuggveny konkret alakja milyen, ugyanakkora magneses teret kapunk, ha a jobb oldalon szereplo integral erteke (vagyis maga az aram) adott. Egyetlen megszoritas van csak: az aramsurusegnek is hengerszimmetriat kell mutatnia, vagyis csak a kozepponttol mert tavolsagtol fugghet, a szogtol nem. fuggveny konkret alakja milyen, ugyanakkora magneses teret kapunk, ha a jobb oldalon szereplo integral erteke (vagyis maga az aram) adott. Egyetlen megszoritas van csak: az aramsurusegnek is hengerszimmetriat kell mutatnia, vagyis csak a kozepponttol mert tavolsagtol fugghet, a szogtol nem.
A masik kerdesre nem a valasz: ket vastag vezetek kozott letrejovo ero nem egyezik meg ket vekony esetevel, ellenben ha az egyik atmeroje elhanyagolhato a masikehoz kepest, akkor a vegeredmeny nem fugg a vastagabb huzal atmerojetol (ld. a fenti ervet).
|
| Előzmény: [288] jonas, 2010-02-22 14:12:38 |
|
| [292] jonas | 2010-02-22 21:32:57 |
 Akkor remélem, valaki, aki fizikához jobban ért, meg tudja ezt válaszolni. Szerintem ez a két hosszú vastag huzal is ugyanannyi erőt fejt ki egymásra, mint a két vékony.
|
| Előzmény: [289] SmallPotato, 2010-02-22 14:23:37 |
|
|
|
| [289] SmallPotato | 2010-02-22 14:23:37 |
 Talán igen. De azért arra nem tenném a nyakamat, hogy két, végtelen hosszú, darabonként mondjuk 1 m átmérőjű és egy alkotó mentén összeérő (azaz tengelyében 1 m távolságra lévő) huzal folyóméterenként ugyanakkora erőt fejt ki egymásra, mint két mondjuk 1 mm átmérőjű, szintén 1 m-re lévő, ugyanakkora áramerősséggel terhelt huzal. Nem tudom eldönteni.
Az elemi áramszálak által adott elemi erők a távolság négyzetével arányosak, így vastag huzal esetében nem átlagolhatók a huzal középvonalába. Szerintem.
|
| Előzmény: [288] jonas, 2010-02-22 14:12:38 |
|
|
|
|
|
|
| [283] Janosov Milán | 2010-02-21 11:44:06 |
 Jóreggelt,
valaki tudna megoldást mutatni a P. 4211.-es feladatra? (Érdekes módon nem lett 3 pontosnál jobb megoldás)
előre is köszönöm, üdv
|
|
|
|
| [280] hbela | 2010-01-29 18:34:44 |
 jó napot kivánok!
örülök a segítségének ! a kérdés a fizikai 11 tk. szerepel a 26 oldal . 2 dik feladat ami a következő egy kötélre felkötött test 1 perc alatt 12 teljes lengést végez .Milyen hosszú kötélen függ a test? erre a válasz elvileg 6.22 m de a képlettel nem jőnn ki. ez az erdmény ugyan ebben tk-ben van megadva .
tiszt. hegedüs béla
|
|
|
| [278] hbela | 2010-01-28 17:21:22 |
 Hellóka segitség !!!! Hogy lehet kiszámolni a fonolinga számitásban a fonal hossszát segitség!!! kösz!
|
|
| [277] lgdt | 2010-01-11 20:31:57 |
 Ez nem teljesen idetartozó téma, de megpróbálok segíteni. Ha jól értem, egy négyszögjelet szeretnél változtatható frekvenciával, amplitúdóval, kitöltési tényezővel és ofszettel. Ezt bármelyik jelgenerátor tudja. Ha mégis te szeretnéd megépíteni az áramkört, akkor emailben tudok segíteni.
|
| Előzmény: [276] óriás, 2010-01-11 20:24:18 |
|
| [276] óriás | 2010-01-11 20:24:18 |
 Üdv!
Valaki tudna nekem segíteni abban, hogy hogyan kell olyan váltakozó áramot generálni, ami a periódus egy részében csak egy bizonyos értéket vesz fel, a többi részében egy más értéket vesz fel, pl.: 0.1s-ig 5V-ot azután meg 0.2s-ig -5V-ot?
|
|
| [275] leni536 | 2010-01-10 12:42:42 |
 Kösz szépen, ilyesmire gondoltam, bár szerintem az elmélet még mindig sumákolva van benne. Konkrétan szó szerint így adták le a gyakon, még a példa is ugyanez volt.
|
| Előzmény: [274] Willy, 2010-01-09 22:15:13 |
|
|
| [273] leni536 | 2010-01-09 18:23:02 |
 Szükségem lenne egy jó forrásra, ahol utána tudok nézni a kanonikus perturbációnak. Elméleti mechanikából tanultuk (pontosabban tétel), de csak gyakorlaton volt róla szó, ott meg eléggé elsumákolták a matekot belőle. Próbálkoztam a Budó, Nagy Károly és Landau mechanika könyvekkel, de egyikben sem találtam.
|
|
| [272] Anzelmus | 2009-10-26 21:02:59 |
 Üdvözlök Mindenkit!
Előszöris elnézést kérek az együgyű kérdésemért.
A minap (mihéten) a kezembe akadt a KöMaL 2007./05 (májusi) száma. Igen rendszertelenül szoktam problémákkal foglalkozni, de általában meg tudom őket oldani. A 315. oldalon lévő P.3988 és P.3990 feladatok azonban megoldatlanok maradtak, megoldásuk érdekelne. A kérdésem, hogy melyik számban található a megoldásuk (azt a lapszámot rendelném meg utólagosan). ((Úgy vettem észre, (néhány meglévő lapszámból levonva a következtetést), hogy durván fél év telik el a feladat kitűzése és a megoldás közlése közt.))
Egy autodidakta feladatmegoldó
|
|
| [271] Geg | 2009-10-25 23:43:02 |
 A normalmodus ismerete azt jelenti, hogy a birtokunkban van a mozgasegyenleteknek olyan megoldasa, melyet egyetlen frekvencia jellemez, vagyis az adott rezgo rendszer reszecskei idoben ugyanolyan utemben harmonikusan rezegnek.
Altalaban tobb fuggetlen, adott frekvenciaju rezgesre kepes egy sokreszecskes rendszer. A mozgasegyenletek linearitasa miatt ezek linearis kombinacioja is megvalosulhat, vagy forditva, egy altalanos rezgest mindig fel lehet bontani normalmodusok osszegere.
|
| Előzmény: [269] Higgs, 2009-10-24 12:40:08 |
|
| [270] SmallPotato | 2009-10-24 23:44:00 |
 Ha lefelé húzzuk, akkor (amennyiben más körülmény nem ismert) nyilván egyenértékű a két irány (hiszen ha átsétálsz a forgástengely másik végére, a jelenség nem változik, de a látott forgásirány igen).
Ami miatt a gyakorlatban nem ritkán mégsem mindegy a forgásirány, az pl. a papírtartó fedele lehet, amely az egyik irányban ráfeszülve a tekercsre, növeli a súrlódást. Ez abban az esetben áll elő, ha a fedél csapágyazása (billenésének tengelye) olyan, hogy a tekercs érintőjének irányába eső erő a tekercs forgástengelye felé ható (és ezáltal a súrlódóerőt fokozó) nyomatékhoz vezet.
|
| Előzmény: [268] psbalint, 2009-10-23 01:24:44 |
|




 , ahol R a korunk sugara. Szemmel lathatoan ekkor fuggetlenul attol, hogy a
, ahol R a korunk sugara. Szemmel lathatoan ekkor fuggetlenul attol, hogy a 


 középponti szögű, l hosszúságú elemére ható sugárirányú erő kifelé mutat és értéke
középponti szögű, l hosszúságú elemére ható sugárirányú erő kifelé mutat és értéke 



