| [301] Geg | 2010-02-28 11:53:17 |
 Az altalanos esetre vonatkozoan lehet latni azt is, hogy ha az integrandusban kicserelem az 1-es es 2-es huzalokat, akkor az eredmeny (-1)-szeresere valtozik? El tudom kepzelni, hogy igy van, csak ranezesre nem latszik (szerintem).
|
| Előzmény: [299] Alma, 2010-02-27 13:10:27 |
|
|
| [299] Alma | 2010-02-27 13:10:27 |
 Vegyünk két hengerszimmetrikus áramsűrűségű, hosszú, henger alakú huzalt, melyek középpontjai egymástól d0 távolságban vannak, sugaruk R1 és R2, áramuk I1 és I2! Ekkor a két huzal által egymásra kifejtett erő hosszegységenként:
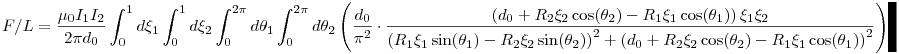
Belátható (Mathematicával kiszámoltam :P), hogy ha az egyik sugár elhanyagolható a másikhoz és d0-hoz képest, akkor a szép négyesintegrál értéke 1. Ez általában nem mondható ki. Egyébként szerintem nem olyan vészes belátni azt, hogy szélsőséges esetben 1 az integrál értéke, de nem lesz teljesen triviális az integrandus, és nem volt kedvem igazából számolgatni.
Végkövetkeztetés: két nem elhanyagolható sugarú henger alakú huzal nem ugyanakkora erővel vonzza egymást, mint két elhanyagolható sugarú, de ha az egyik huzal sugara elhanyagolható minden más mérethet képest, akkor ugyanakkora az erőhatás, mint két elhanyagolható sugarú huzalnál.
|
|
|
| [297] wernerm | 2010-02-24 07:29:01 |
 Szervusztok, Jó reggelt!
A feladatot én javítottam. Sajnos a megoldók többnyire az itt is olvasható megoldást csinálták, ami nem jó, ugyanis figyelembe kell venni, hogy a cső egyes szálai vonzzák egymást. Ezt kétféle módon tehetjük meg:
a.) Összegezni kell az egyes szálakra.
b.) amikor egy ívelemre ható erőt számolunk, figyelembe kell vennünk, hogy a falban a mágneses tér szépen 0-ra esik le, mire a szélére érünk.
Viszonylag egyszerűen kijön, hogy "B" helyett "B"/2-vel kell számolni.
üdv: Werner Miklós
|
| Előzmény: [283] Janosov Milán, 2010-02-21 11:44:06 |
|
|
| [295] Geg | 2010-02-23 23:52:23 |
 A korabban leirtak szerint egy huzal altal keltett magneses indukcio erteke a huzaltol adott tavolsagra nem fugg attol, hogy milyen annak vastagsaga (hengerszimmetrikus aramsuruseget felteve). Emiatt ha a vastag huzaltol adott tavolsagra levo (vele parhuzamos), elhanyagolhato vastagsagu huzalra hato erot akarjuk szamolni, akkor nyilvan ismet nem szamit az, hogy a masik milyen vastag, mivel a vekony huzal helyen a magneses indukcio nagyon jo kozelitessel nem valtozik.
Ellenben ha a ket huzal egymassal osszemerheto vastagsagu, akkor bar az egyik huzal altal letrehozott magneses indukcio ertekere vonatkozo allitas tovabbra is ervenyes, annak helyrol helyre valo valtozasa miatt az erohatas konkretan attol fog fuggni, hogy megis milyen vastag a masik huzal. A szamolas soran fel kell osztani az utobbi huzalt infinitezimalisan vekony darabkakra (az ezekre hato elemi erojarulekok szamitasa soran nem kell a magneses indukcio inhomogenitasaval foglalkozni), majd az elemi erodarabokat ossze kell adni (ki kell integralni) a teljes feluletre.
Ezzel nagyjabol analog a SmallPotato [289]-es hozzaszolasaban elhangzo erv.
|
| Előzmény: [294] jonas, 2010-02-23 11:17:15 |
|
| [294] jonas | 2010-02-23 11:17:15 |
 Hogyha az egyik huzal sokkal vékonyabb, mint a másik, akkor a vastag huzalban hengerszimmetrikus az áramsűrűség?
Ha igen, akkor mitől változna ez meg, ha a másik vezeték is vastagabb lesz? Hiszen ha az első vezeték vékonyról vastagra változik, de továbbra is hengerszimmetrikusan folyik benne az áram, ezért ugyanolyan elektromágneses teret csinál, mint ha vékony lenne, akkor a másik vezeték nem veheti észre, hogy az egyik vastag vagy vékony, tehát ha a másikat is vastagra változtatod, akkor abban is hengerszimmetrikusan folyik az áram, és ugyanolyan erővel kell vonzaniuk egymást, mint két vékony vezetéknek.
Ha viszont nem hengerszimmetrikus az áram, akkor miért lesz mégis ugyanaz a két vezeték közti erő függetlenül a vastag vezeték átmérőjétől?
|
| Előzmény: [293] Geg, 2010-02-23 10:47:13 |
|
| [293] Geg | 2010-02-23 10:47:13 |
 Valoban nem szukseges, hogy a huzal atmeroje elhanyagolhato legyen. Ugyanis Ampere torvenye szerint
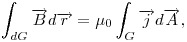
ahol a bal oldalon egy zart gorbe menten kell integralni a magneses indukcio vektorat, jobb oldalon pedig a gorbe altal kijelolt feluletre kell integralni az aramsuruseget. Legyen a szoban forgo gorbe egy kor, melynek kozeppontja atmegy a huzal kozeppontjan. Hengerszimmetriat feltetelezve a bal oldal B×2R , ahol R a korunk sugara. Szemmel lathatoan ekkor fuggetlenul attol, hogy a , ahol R a korunk sugara. Szemmel lathatoan ekkor fuggetlenul attol, hogy a 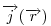 fuggveny konkret alakja milyen, ugyanakkora magneses teret kapunk, ha a jobb oldalon szereplo integral erteke (vagyis maga az aram) adott. Egyetlen megszoritas van csak: az aramsurusegnek is hengerszimmetriat kell mutatnia, vagyis csak a kozepponttol mert tavolsagtol fugghet, a szogtol nem. fuggveny konkret alakja milyen, ugyanakkora magneses teret kapunk, ha a jobb oldalon szereplo integral erteke (vagyis maga az aram) adott. Egyetlen megszoritas van csak: az aramsurusegnek is hengerszimmetriat kell mutatnia, vagyis csak a kozepponttol mert tavolsagtol fugghet, a szogtol nem.
A masik kerdesre nem a valasz: ket vastag vezetek kozott letrejovo ero nem egyezik meg ket vekony esetevel, ellenben ha az egyik atmeroje elhanyagolhato a masikehoz kepest, akkor a vegeredmeny nem fugg a vastagabb huzal atmerojetol (ld. a fenti ervet).
|
| Előzmény: [288] jonas, 2010-02-22 14:12:38 |
|
| [292] jonas | 2010-02-22 21:32:57 |
 Akkor remélem, valaki, aki fizikához jobban ért, meg tudja ezt válaszolni. Szerintem ez a két hosszú vastag huzal is ugyanannyi erőt fejt ki egymásra, mint a két vékony.
|
| Előzmény: [289] SmallPotato, 2010-02-22 14:23:37 |
|
|
|
| [289] SmallPotato | 2010-02-22 14:23:37 |
 Talán igen. De azért arra nem tenném a nyakamat, hogy két, végtelen hosszú, darabonként mondjuk 1 m átmérőjű és egy alkotó mentén összeérő (azaz tengelyében 1 m távolságra lévő) huzal folyóméterenként ugyanakkora erőt fejt ki egymásra, mint két mondjuk 1 mm átmérőjű, szintén 1 m-re lévő, ugyanakkora áramerősséggel terhelt huzal. Nem tudom eldönteni.
Az elemi áramszálak által adott elemi erők a távolság négyzetével arányosak, így vastag huzal esetében nem átlagolhatók a huzal középvonalába. Szerintem.
|
| Előzmény: [288] jonas, 2010-02-22 14:12:38 |
|
|
|
|
|
|
| [283] Janosov Milán | 2010-02-21 11:44:06 |
 Jóreggelt,
valaki tudna megoldást mutatni a P. 4211.-es feladatra? (Érdekes módon nem lett 3 pontosnál jobb megoldás)
előre is köszönöm, üdv
|
|
|
|
| [280] hbela | 2010-01-29 18:34:44 |
 jó napot kivánok!
örülök a segítségének ! a kérdés a fizikai 11 tk. szerepel a 26 oldal . 2 dik feladat ami a következő egy kötélre felkötött test 1 perc alatt 12 teljes lengést végez .Milyen hosszú kötélen függ a test? erre a válasz elvileg 6.22 m de a képlettel nem jőnn ki. ez az erdmény ugyan ebben tk-ben van megadva .
tiszt. hegedüs béla
|
|
|
| [278] hbela | 2010-01-28 17:21:22 |
 Hellóka segitség !!!! Hogy lehet kiszámolni a fonolinga számitásban a fonal hossszát segitség!!! kösz!
|
|
| [277] lgdt | 2010-01-11 20:31:57 |
 Ez nem teljesen idetartozó téma, de megpróbálok segíteni. Ha jól értem, egy négyszögjelet szeretnél változtatható frekvenciával, amplitúdóval, kitöltési tényezővel és ofszettel. Ezt bármelyik jelgenerátor tudja. Ha mégis te szeretnéd megépíteni az áramkört, akkor emailben tudok segíteni.
|
| Előzmény: [276] óriás, 2010-01-11 20:24:18 |
|





 , ahol R a korunk sugara. Szemmel lathatoan ekkor fuggetlenul attol, hogy a
, ahol R a korunk sugara. Szemmel lathatoan ekkor fuggetlenul attol, hogy a 

 középponti szögű, l hosszúságú elemére ható sugárirányú erő kifelé mutat és értéke
középponti szögű, l hosszúságú elemére ható sugárirányú erő kifelé mutat és értéke 
