| [69] lorantfy | 2005-05-01 12:00:24 |
 Ezután nézzük mi a hiba az energiákkal felírt megoldásban.
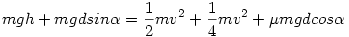
Az első szakaszon: 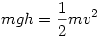 , ezt kihúzhatjuk. Nézzük mi marad, ha , ezt kihúzhatjuk. Nézzük mi marad, ha  =tg =tg -t beírjuk. -t beírjuk.
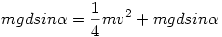
Ez nyilván nem igaz. Miért? Mert a súrlódási munka már tartalmazza a forgási energiát, így ez a jobb oldalon kétszer szerepel. Ha kihúzzuk, azonosság marad, ebből így nem lesz megoldás!
Továbbá hibás a 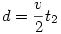 képlet. A sebesség a második szakaszon állandó, így d=v1.t2 képlet. A sebesség a második szakaszon állandó, így d=v1.t2
(A piros éa zöld hullámos aláhúzásokat a WORD-ben le lehet venni az Eszközök/Beállítások/Helyesírás/Helyesírási- ellenőrzés beíráskor ill. Nyelvhelyesség-ellenőrzés beíréskor pipák kivételével!)
|
| Előzmény: [66] riiaa, 2005-04-29 06:59:26 |
|
| [68] lorantfy | 2005-05-01 10:41:35 |
 Kedves Riiaa!
Mielőtt hibát keresek más megoldásában én először meg szoktam csinálni a példát, ahogy én gondolom.
A mozgás első szakasza, AB világos. a=g/2, s=3,6 m, 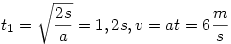 . .
A második szakaszon (BC) a súrlódási erő Fs= mgcos mgcos és mivel és mivel  =tg =tg , Fs=mgsin , Fs=mgsin , ami éppen megegyezik a gravitációs erő lejtővel párhuzamos komponensével. Így a második szakaszon a hengerre ható erők eredője nulla, tehát a tömegközéppont sebessége nem változik. , ami éppen megegyezik a gravitációs erő lejtővel párhuzamos komponensével. Így a második szakaszon a hengerre ható erők eredője nulla, tehát a tömegközéppont sebessége nem változik.
A második szakasz addig tart, míg a súrlódási erő felpörgeti a hengert  =v1/r szögsebességre. =v1/r szögsebességre.
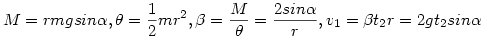 amiből amiből
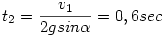
A második szakasz hossza BC=d=v1t2=3,6m. A súrlódási erő Fs=20N,Ws=72J
Mivel a súrlódási erő pörgeti fel a hengert, a súrlódási munkából 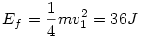 hasznosul és Q=36 J lesz a hőveszteség. hasznosul és Q=36 J lesz a hőveszteség.
Remélem jól gondoltam!
|
| Előzmény: [66] riiaa, 2005-04-29 06:59:26 |
|
|
|
|
| [64] galopin | 2005-04-27 23:27:36 |
 Sziasztok.
Köszönetet szeretnék mondani ..vagyis irni nektek amiért ilyen gyorsan és ilyen sokat tudtatok nekem segiteni a harkályos témában ...ezekkel az infokkal már nagyon jol el tudok indulni. nagyon nagyon hálás köszönetem érte:) mindenkinek további jo fizikázást kivánok. és ezer köszi a segitséget.
üdv.
|
|
| [63] Drin | 2005-04-27 19:22:55 |
 Nem hangzik rosszul, de ez eléggé körülményes mérés lenne (legalábbis nekem), én inkább valami elméletibb megoldásra gondoltam. Bár lehet, hogy az álltalam használt modellt is igazítani kéne a "valósághoz", de eddíg akárhányszor is néztem a pezsgőtabletta oldódását valahogy mindíg úgy tűnt, hogy félgömbszerű buborékok vannak a felszínén. Amúgy elmélet útján meg lehet becsülni, hogy kb milyen határok között változhat a sugár. Pl ha felírod a diff-egyenleteket akkor amikor kiszámolod, hogy kb oldódástól kezdve mennyi időn bellül fog a tablettára ható felhajtóerő és gravitációs erő egyensúlyt tartani akkor az időre kapott kifejezésből kihozható, de ez is csak alsó-felső korlát. Mondjuk talán be lehetne vezetni valami állandót az oldódás folyamatára amiből aztán ki lehetne gyötörni valahogy a sugarat, de ez elég esélytelen.
|
| Előzmény: [62] Fálesz Mihály, 2005-04-27 12:34:50 |
|
| [62] Fálesz Mihály | 2005-04-27 12:34:50 |
 Egy ötlet. (Lehet, hogy teljesen használhatatlan.)
A tablettára tapadó gáz mennyisége a tabletta felszínének nagyságától függ.
A tablettát vékonyabbra csiszolod, és megkeresed azt a vastagságot, amikor éppen lebeg. Ebben az esetben a tabletta sűrűségéből kiszámolhatod, hogy mennyi gáz tapad rá összesen.
|
| Előzmény: [61] Drin, 2005-04-27 10:12:27 |
|
| [61] Drin | 2005-04-27 10:12:27 |
 Sziasztok!
Múltkor csináltam egy phys feladatot és egy (szerintem) fontos lépést kivéve lényegében kész a feledata. A feladat az, hogy a pezsgőtabletta méretét adjuk meg az idő függvényében. Az oldódó pezsgőtabletához olyan modelt választttam, hogy adott pillanatban a pezsgőtabletta (minek alakja kjör alakú hasáb) felszínén sok félgömb alakú "kis gáztartály" van egyenletesen elhelyezkedve a vízzel érintkező felületen amikben az oldódás során a tablettából "kioldott " gáz van (álandó nyomáson és állandó hőmérsékleten, valamint feltételezem, hogy a mólszám se változik a "gáztatrályban" és a további kioldott anyag a félgömbök között "kiszivárog"). Feltételeztem továbbá, hogy a folyamat során a víz koncentrációja közel állandó és (nyilván nem egy mély víztatrályba dobjuk a tablettát) a "gáztatrályokban" a nyomás is állandó (a légkörivel egyenlő) mivel a pohár aján a víz hidrosztatikai nyomása jóval kisebb mint a légköri nyomás. A megoldás során azonban nem tudtam még csak közelítőleg se meghatározni a félgömb alakú "gáztaretályok" sugarát, térfogatát ? Ha van valami ötletetek akkor légyszi ítjatok. Előre is kösz.
|
|
| [60] lorantfy | 2005-04-22 18:03:54 |
 "Guinness Book of Records"-szerint:
The beak of the red-headed woodpecker hits the bark of a tree with an impact velocity of over 21 km/h, subjecting the bird's brain to a deceleration of approximately 10 g when its head snaps back.
Jó lenne tudni a kép milyen expozíciós idővel készült, mert a bemozdulás kb. 2 cm és ebből már lehetne következtetni a sebességre. Ha 1/100-al akkor 2 m/s körül volt a sebesség. A max. amplitudó 10 cm körüli lehet.
|
 |
|
| [59] lorantfy | 2005-04-22 09:41:09 |
 Valóban a csőr rugalmasságát is meg kell vizsgálni. Az ütközés a kritikus pont. Légkalapács effektus. A légkalapács nyele rázkódik, de nem üt erősen. Egy beépített rugó elnyeli az energiát. Nyilván a természet is kitalált valamilyen energia elnyelő rendszert a harkály csőréhez.
|
| Előzmény: [57] Fálesz Mihály, 2005-04-22 09:21:58 |
|
| [58] Hajba Károly | 2005-04-22 09:28:40 |
 Kedves galopin!
Goole(harkály fizika)
Az első szálon továbbmenve ERRE leltem. Innen folytathatod a keresést.
A Gugli eredménylistában van egy rahedli szemét, de hát guberálni tudni kell. :o)
Jó kutakodást!
HK
|
| Előzmény: [55] galopin, 2005-04-21 21:46:01 |
|
| [57] Fálesz Mihály | 2005-04-22 09:21:58 |
 Szerintem inkább két, különböző körfrekvenciájú fél rezgőmozgásra, ha tetszik, labdapattogásra hasonlít. A kisebbik gyorsulás és nagyobb (fél) amplitúdó akkor van, amikor eltávolodik a fától, és a fa felé gyorsul. A nagyobb gyorsulás pedig akkor van, amikor koppan.
A kérdés igazából az, hogy a rengeteg koppanást hogy bírja ki agyrázkódás nélkül. Egyszer azt hallottam, hogy a csőre és a koponyája között egy nagyon rugalmas szövet van, de forrást ebben a pillanatban nem tudok.
|
| Előzmény: [56] lorantfy, 2005-04-22 08:44:29 |
|
| [56] lorantfy | 2005-04-22 08:44:29 |
 Közelítsük a kopogtatást harmonikus rezgőmozgéssal. A harkály méreteiből meg lehet becsülni a max. kitérést. A kopogtatás hallható hangjából megbecsüljük a frekvenciát. Ezekből kiszámoljuk a max. gyorsulást amit el kell viselnie. Hozzá még tonna rizsa, pár kép és kész a dolgozat.
|
| Előzmény: [55] galopin, 2005-04-21 21:46:01 |
|
| [55] galopin | 2005-04-21 21:46:01 |
 Sziasztok. egy nagy segítséget szeretnék töletek kérni. az lenne a problémám hogy egy fizika esszét kellene irnom arrol hogy a harkály kopogtatja a fákat de nem kap agyrászkódást ...cimmel. sajnos a könyvtárakban és az interneten sem igazán találtam ezzel kapcsolatos információt. kellene irni a harkályrol ugy általánosan és fizikai bizonyitással is hogy miért is van ez. nem tudom hol kellene megfogni egyáltalán a témát:( abban szeretném a segítségeteket kérni hogy ha modotokban áll légyszives irjátok már meg nekem hol találok ehez a témához megfelelö szakirodalmat? ...mind biologiai mind fizikai vonalon vagy a kettöt együtt biofizikain:) légyszives segitsetek nekem mert szorit a határidö (május 5) hogy ezt a 3-4oldalas irományt leadásra kell bocsátanom. elöre is köszi ha tudtok segiteni Krisz
|
|
| [54] Drin | 2005-04-19 07:21:31 |
 Este megnéztem mi lesz az y(x), tenyleg érdekes bár én a(x)-et b(x)-et a köv képpen adtam meg: a(x)=a0(L-x)/L, b(x)=b0(L-x)/L, L a gúla magassága, a(x) b(x) meg a hasonlóságok alapjan megy, ugyanígy az erőkar+tömeg is csak ekkor (L-x)/L a hjarmadik hatvanyon van. Szép másodfokú lett, bár a cikk alapján azért fennáll: L >>a0,b0 mert ez vegülis a közepvonal lehajlasa ( bar a L >>a0,b0 nem ennyire erős feltétel). Viszont kiváncsi lennék, hogy csonkagúla esetén mi lenne az y(x) bár ahogy elnéztem a diff-egyenletet ehhez inkább progi kéne.
|
| Előzmény: [53] Geg, 2005-04-18 21:12:44 |
|
|
| [52] Drin | 2005-04-18 20:52:06 |
 Szia Geg!
Köszi a gyors választ. Akkor végülis a phys tanáromnak volt igaza. Tényleg gúla lesz, bár a szöveg nem említi, hogy csonka-e de gondolom ettől el lehet tekinteni. Ínnét már tényleg gyors a megoldas: M(x)=E*I(x)*G ... stb, bár gondolom 0 <= x <= 1.
|
| Előzmény: [51] Geg, 2005-04-18 19:01:16 |
|
| [51] Geg | 2005-04-18 19:01:16 |
 Vedd ugy, hogy a = a0*(l-x)/l es b = b0*(l-x)/l, tovabba a differencialegyenlet felirasakor figyelembe kell venni, hogy a tomegeloszlas emiatt nem egyenletes, illetve azt is, hogy a felulet masodrendu nyomateka (I) sem allando, hanem a tavolsag fuggvenye. A megoldas innen integralassal adodik (nem szamoltam ki).
|
| Előzmény: [50] Drin, 2005-04-18 15:34:05 |
|
| [50] Drin | 2005-04-18 15:34:05 |
 Sziasztok!
A KöMaL-ban megjelent egy cikk a hajlításról. A cikk végén található egy feladvány: " Érdekes annak a gerendának a ... ". Az lenne a kérdésem, hogy ennek a gerendának az alakja milyen pontosan ? Mert nekem nem igazán sikerült értelmezni. Személy szerint úgy gondolom, hogy oldalnézetből olyan mint a cikkben a gerendák csak fellülről nézve egyenlő szárú háromszög, bár ennek nem kell feltétlenül teljesülnie. Viszont a fizika tanárom azt mondta, hogy ez egy gúla lesz, vagy csonka vagy teljes, bár szerintem ha ez lesz akkor inkább teljes a diff-egyenlet miatt. Ezek alapján nem tudtam dűlőre jutni, úgyhogy ez úton kérném e segítségetek.Előre is köszi.
|
|
| [49] lorantfy | 2005-03-13 22:12:15 |
 Kedves Joe!
Jó lenne, ha jobban körülírnád, vagy mondanál egy konkrét példát, hogy mire gondolsz!
Tehetetlenségi erőnek szokták nevezni egy gyorsuló koordináta rsz-ben fellépő fiktív (nem valódi) erőt.
Ha egy űrhajó belső terében lebeg egy test és az űrhajó gyorsulva kezd mozogni, a lebegő test az űrhajóhoz képest ellenkező irányba kezd gyorsulva mozogni, pedig rá nem hat semmilyen erő. Az űrhajóhoz rögzített koordináta rsz-ben úgy tűnik ezt a testet F=ma erő gyorsítja. Ezt a nem létező erőt szokták tehetetlenségi erőnek nevezni.
Mivel ez az erő nem létezik ellenereje sincs.
Éppen ezen gondolkodott el mélyebben Einstein apánk és rájött, hogy ez a nem létező erő megfeleltethető a gravitásciós erőnek és létrehozta az ált rel. elm-t. Tehát egy g gyorsulással mozgó űrhajóban pontosan úgy érezzük magunkat (úgy zajlanak le a fiz. kisérletek) mint a Föld g gyorsulású grav. teréven.
|
| Előzmény: [48] joe, 2005-03-13 20:16:27 |
|
| [48] joe | 2005-03-13 20:16:27 |
 Üdvözlök mindenkit!
Egy elég amatőrnek tűnő kérdésem van: Hol a tehetetlenségi erő ellenereje?
|
|
| [47] Mate | 2005-03-07 12:33:35 |
 Kedves László!
Azt hiszem, nem derült ki világosan a hozzászólásodból, hogy végül mekkora erőt fejt ki egymásra két mágnes.
A mágneses Coulomb-törvény valóban igaz, azonban csak mágnespólusok közötti erőhatást ír le. Egy mágnes azonban két pólusból áll, amely pólusok elég közel vannak egymáshoz (főleg a kicsiny neodímium mágnes esetén), tehát dipólus közelítéssel kell számolnunk.
Ha szükséges, leírhatom a számolást, de most csak annyit, hogy a mágneses Coulomb-törvényt felírod a két mágnes 2-2 pólusa között (legyen d a mágnes hossza, r pedig a távolságuk), és d/r-rel tartasz nullához...
Így azt kapjuk, hogy két dipólus között ható erő a távolság -4. hatványával arányos, és nem kell tudni a póluserősségeket, csak a mágnesek dipólnyomatékát.
Egyébként elektromos töltésekre egyszerű megjegyezni: Két töltés közötti erő a távolság -2., egy töltés és egy dipólus közötti erő a távolság -3., két dipólus közötti erő a távolság -4. hatványával arányos. Tanulságos kiszámolni két kvadrupól által kifejtett erő távolságfüggését.
|
| Előzmény: [45] lorantfy, 2005-03-06 13:00:03 |
|
|
| [45] lorantfy | 2005-03-06 13:00:03 |
 Hello Valv!
Két mágnes között ható erőt a mágneses Coulomb tv. írja le, hasonló mint a két töltés között ható erőt-tv.
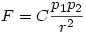
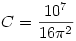 me: me: 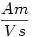
p : póluserősség me: 1 Weber (Wb)=1 Vs
Szerintem ebből csak annyit tudsz használni, hogy az erő a távolság négyzetével csökken. A póluserősségeket legfeljebb méréssel tudod meghatározni az adott mágnesnél.
|
| Előzmény: [42] Valv, 2005-02-28 09:12:13 |
|



 =tg
=tg -t beírjuk.
-t beírjuk.  =v1/r szögsebességre.
=v1/r szögsebességre. 





