KöMaL Problems in Physics, April 2018
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on May 10, 2018. |
M. 377. Create a short circuit across a solar cell by connecting an ammeter across it. Investigate how the current depends on the angle of incidence of the ,,direct sun rays''. Do not forget to set a proper measurement range for the ammeter.
(6 pont)
 |
Problems with sign 'G'Deadline expired on May 10, 2018. |
G. 633. Is it possible that after a free kick is awarded to a team on a soccer pitch, the ball bounces from the crossbar of the goal behind the goal line and from the ground it bounces outward towards the pitch?
(3 pont)
solution (in Hungarian), statistics
G. 634. The inner ring of the ball-bearing shown in the figure is at rest, the centres of the balls are undergoing circular motion at a speed of 0.2 m/s. What is the number of revolution of the outer ring, if \(\displaystyle r=3\) cm, \(\displaystyle R=4\) cm?
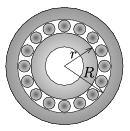
(3 pont)
solution (in Hungarian), statistics
G. 635. There is some water at a temperature of \(\displaystyle 0~{}^\circ\)C in a bowl. Some part of it is taken out and frozen to a piece of ice at a temperature of \(\displaystyle 0~{}^\circ\)C, then it is put back to the bowl, in which it floats on the top of the remaining water in it.
\(\displaystyle a)\) Will the top of the ice be at a greater height than the original water level?
\(\displaystyle b)\) Which one has the greater gravitational potential energy: the water ice system, or the original water in the bowl?
(3 pont)
solution (in Hungarian), statistics
G. 636. How far may the city Miskolc be from the road sign in which the following warning is written: ``You cannot even save 8 minutes till Miskolc. Is it worth it?'' (The speed limit for the highways in Hungary is 130 km/h.)

(4 pont)
 |
Problems with sign 'P'Deadline expired on May 10, 2018. |
P. 5023. The speed of an object sliding down a slope of angle of elevation \(\displaystyle 25^\circ\), is one-quarter of the final speed that the object could have reached if there was no friction. What is the coefficient of kinetic friction?
(4 pont)
solution (in Hungarian), statistics
P. 5024. An object of mass \(\displaystyle m\) is suspended by a rubber thread of unstretched length \(\displaystyle l\), and of force (spring) constant \(\displaystyle k\). Then the object, which is in equilibrium, is pulled slowly, such that it moves along a horizontal line through its initial position. What is the magnitude of the pulling force, which belongs to the position when the rubber thread makes an angle of \(\displaystyle \varphi\) with the vertical?
Data: \(\displaystyle \ell=0.5\) m, \(\displaystyle \varphi=30^\circ\), \(\displaystyle m=0.4\) kg, \(\displaystyle k=10\) N/m.
(4 pont)
solution (in Hungarian), statistics
P. 5025. Torricelli's experiment was carried out by means of a thick-walled glass tube. The inner diameter of the tube is \(\displaystyle 1~\rm cm^2\) and its outer diameter is \(\displaystyle 3~\rm cm^2\). The mass of the tube is 624 g and it emerges into the mercury to a depth of 2 cm.
By what force should the tube be hold?
(4 pont)
solution (in Hungarian), statistics
P. 5026. A thin ring of mass \(\displaystyle m\) and of radius \(\displaystyle R\) is made swing with small amplitude in two different ways. In one of the cases the ring is supported by a horizontal cylinder of radius \(\displaystyle r\), displaced a bit and then released. In the other case a thin pin of length \(\displaystyle r\) and of negligible mass is attached to the inside part of the ring, such that it points towards the centre of the ring, and the ring is supported by this pin while it swings. The motion of the ring is planar in both cases.
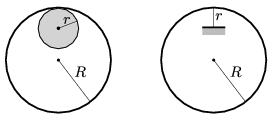
In which case will the period of the oscillation be larger?
(5 pont)
solution (in Hungarian), statistics
P. 5027. An experimental bicycle was powered with a rocket engine, and happened to reach the speed of 333 km/h. Starting from rest it reached the speed of 100 km/h in 1.1 s, 200 km/h in 2.5 s, 300 km/h in 4.3 s and in 4.8 seconds it reached the speed of 333 km/h.

When did it reach its greatest acceleration and what was the value of this acceleration? How much distance did it cover until it reached its greatest velocity? What was the total mass if the thrust of the rocket was 4.2 kN?
(4 pont)
solution (in Hungarian), statistics
P. 5028. Some air is confined in a 1 m long cylinder-shaped container. The cylinder is moved at a constant acceleration in the direction of its symmetry axis, while the temperature of the air in it is kept constant \(\displaystyle T=273\) K. At what value of the acceleration \(\displaystyle a_0\), would the pressure at the front of the cylinder be
\(\displaystyle a)\) 0.1% less than the pressure at the back of the cylinder?
\(\displaystyle b)\) half of the pressure at the back of the cylinder?
Hint: The density of atmospheric air as a function of the height \(\displaystyle h\) – if the temperature is constant 273 K – can be calculated with the barometric formula: \(\displaystyle \varrho(h)= \varrho_0{\rm e}^{-\frac{Mgh}{RT}}\), where \(\displaystyle M\) is the average molar mass of the air, and the density drops to half of the sea level value at about 5500 m above sea level.
(5 pont)
solution (in Hungarian), statistics
P. 5029. An iron cube is placed to the top of an aluminium cube having the same mass as the iron cube.
\(\displaystyle a)\) What is the average density of the gained metal object?
\(\displaystyle b)\) By what amount measured in \(\displaystyle \rm g/dm^3\) does the average density of the object change if its temperature is increased by \(\displaystyle 15~{}^\circ\)C?
(4 pont)
solution (in Hungarian), statistics
P. 5030. Small metal spheres of mass \(\displaystyle m\) were attached to an insulating rod of mass \(\displaystyle m\) and of length \(\displaystyle 4d\). There is another metal sphere (with a hole through it) of mass \(\displaystyle m\), at a distance of \(\displaystyle d\) from one of the ends of the rod. This sphere can move frictionlessly along the rod. All the three metal spheres are given a charge of \(\displaystyle Q\), and the system is released – the system is floating in a space station.
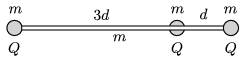
What will the maximum speed of the sphere in the middle be and how much distance will the spheres move until the maximum speed is reached?
(4 pont)
solution (in Hungarian), statistics
P. 5031. The capacitance of the condensers in the circuit shown in the figure is \(\displaystyle C=4~\mu\)F. The system is connected to a constant voltage supply of value \(\displaystyle U=16\) V.
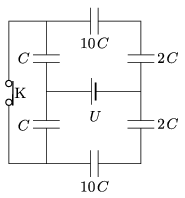
\(\displaystyle a)\) Calculate the charge of the condensers and the voltage across them.
\(\displaystyle b)\) The switch K is opened. How much charge flows through the voltage supply until the new equilibrium state is reached?
(4 pont)
solution (in Hungarian), statistics
P. 5032. At what speed will the nucleus of a \(\displaystyle {}^{220}_{~86}\rm Rn\) atom be pushed back when it ejects an \(\displaystyle \alpha\) particle? The mass of the radon isotope is \(\displaystyle 220.011\,394\) u and the mass of the remaining \(\displaystyle {}^{216}_{~84}\rm Po\) polonium isotope is \(\displaystyle 216.001\,915\) u.
(4 pont)
solution (in Hungarian), statistics
P. 5033. The angular momentum of the interstellar cloud of mass \(\displaystyle M\), consisting of cosmic dust and gases, is \(\displaystyle N\). Due to the internal gravitational effects the total material of the cloud forms two small spheres, thus a binary star system is created.
\(\displaystyle a)\) What is the period \(\displaystyle T_\text{star}\) of the binary star revolving about its centre of mass, if the paths of the stars are circular and the masses of the stars are \(\displaystyle m_1\) and \(\displaystyle m_2\)? (\(\displaystyle m_1+m_2=M\) and \(\displaystyle m_1\le m_2\).)
\(\displaystyle b)\) What can the distance between the stars be?
\(\displaystyle c)\) If the distance between the two stars is not exactly constant, but varies with a small amplitude, what may the period of this variation be?
(6 pont)
Upload your solutions above.
