KöMaL Problems in Physics, December 2019
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on January 10, 2020. |
M. 391. Using a soft graphite pencil, draw marks to a piece of paper. Measure the thickness of the graphite layer.
(6 pont)
 |
Problems with sign 'G'Deadline expired on January 10, 2020. |
G. 689. The tracks of a toy tracked vehicle are suspended by two wheels whose centres are at a distance of 22 cm from each other. How long does a chain-link remain at rest on the ground, if the speed of the toy is 4 cm/s? How does this time depend on the radius of the wheel?
(3 pont)
solution (in Hungarian), statistics
G. 690. There are two alike glasses filled brimful with water on the table. In one of them a ping-pong ball is floating on the surface of the water. Which glass exerts a greater force on the table?
(3 pont)
solution (in Hungarian), statistics
G. 691. Two inclined planes of the same elevation angle are facing towards each other. They are connected with a short frictionless section. One of the planes is so slippery that friction is negligible on it, whilst the other plane is a bit rough (so an object released on this plane slides down with some acceleration). A small object is released without initial speed from the same height once from one of the planes and next from the other plane. In which case will it go higher up on the other plane? For example let the angle of elevation be \(\displaystyle 30^\circ\), the coefficient of kinetic friction on the rough plane be 0.2, and the object is released from a height of 1 metre.
(4 pont)
solution (in Hungarian), statistics
G. 692. Mountaineers, when they are climbing mountains, make drinking water from fresh snow. They warm up 4 dl water to \(\displaystyle 80\,{}^\circ\)C, and then they put 5 snowballs of diameter 8 cm, and of temperature \(\displaystyle 0\,{}^\circ\)C into it. They gain water at a temperature of \(\displaystyle 16\,{}^\circ\)C. What is the density of the snowball?
(4 pont)
 |
Problems with sign 'P'Deadline expired on January 10, 2020. |
P. 5175. The wheelbase (distance between the axles of the front and the rear wheels) of a car is 2.6 m and its track width is 1.8 m. (The track width is measured as the distance between the centres of the tread areas of the tires of the two front or two rear wheels when the car is moving along a straight line.) The car completes a whole circle on a level road which is covered with fresh snow. How many car tire traces can be observed in the snow? What is the diameter of each circular trace if the diameter of the smallest circle is 16 m?
(4 pont)
solution (in Hungarian), statistics
P. 5176. A student is standing with horizontally stretched arms. The mass of his arm is 3 kg, and the centre of mass of the arm is exactly at the elbow of the student, which is at a distance of 27.5 cm from the joint at the shoulder of the student about which the arm can be turned, as it is shown in the figure. The force exerted in the deltoid muscle of the student encloses an angle of \(\displaystyle 15^\circ\) with the horizontal, and its point of application is at a distance of 12 cm from the joint in the shoulder. Using calculation or classical construction, determine the force exerted by the deltoid muscle of the student.
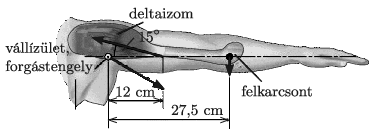
(4 pont)
solution (in Hungarian), statistics
P. 5177. A 500 g object is attached to a vertical compression-expansion spring of spring constant 400 N/m. On the object – next to the attachment of the spring – there is a 100 g metal ring at rest. The object and the ring is suddenly given an initial downward speed of \(\displaystyle v_0\). During their motion together, when their acceleration is the greatest, the apparent weight of the ring becomes three times as much as its original weight was. How much time elapses from the beginning of their motion until the ring becomes weightless?
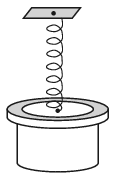
(4 pont)
solution (in Hungarian), statistics
P. 5178. There is a spring gun of negligible mass fixed at an angle of \(\displaystyle \alpha = 30^\circ\) to a cart of mass \(\displaystyle m\) on the horizontal ground. The spring gun shoots a bullet in two cases. In the first case the cart can move freely, whilst in the other the cart is fixed. The vertical displacement of the bullet in the first case is \(\displaystyle h_1\), and in the second case it is \(\displaystyle h_2\). Determine the ratio \(\displaystyle h_2/h_1\).
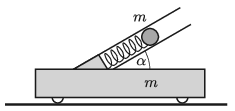
(5 pont)
solution (in Hungarian), statistics
P. 5179. A hockey puck of mass \(\displaystyle m\) is sliding at a speed of \(\displaystyle v_1\), and then it bounces back elastically and perpendicularly from an ice hockey stick which was moved at a constant speed of \(\displaystyle u\).
\(\displaystyle a)\) After bouncing back, what is the speed \(\displaystyle v_2\) of the puck?
\(\displaystyle b)\) What should the speed of the stick be in order that after the collision the puck stop?
(4 pont)
solution (in Hungarian), statistics
P. 5180. A sample of monatomic ideal gas is taken through the cyclic process \(\displaystyle ABCA\) shown in the figure. What is the efficiency of the cyclic process if the highest temperature of the gas (measured in kelvins) is nine times as big as the lowest temperature of the gas?
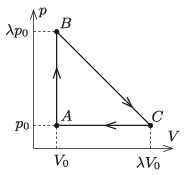
(5 pont)
solution (in Hungarian), statistics
P. 5181. There is a thin negligible-mass piston at exactly the middle of the height of a container which is open at its top and is shown in the figure. The volume of the enclosed air is \(\displaystyle V_0\), and the atmospheric pressure is 76 cmHg. Slowly mercury is poured to the piston, until the level of the mercury reaches the rim of the container. How much does the piston move? (The container and the piston are thermal insulators; and we have \(\displaystyle h=38\) cm.)
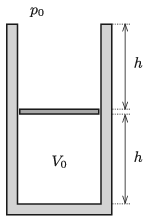
(4 pont)
solution (in Hungarian), statistics
P. 5182. The defroster of the rear window of a car consists of 13 very thin, nearly invisible pieces of wire glued into the glass of the window. The resistivity of the material of the wires is \(\displaystyle 8.8\cdot 10^{-7}~\Omega\rm m\). Each wire is 1.3 m long and they are all connected to the 12 V electric generator of the car in parallel. The defroster melts 21 g \(\displaystyle 0\,{}^\circ\)C ice to \(\displaystyle 0\,{}^\circ\)C water in 2 minutes. Suppose that all the energy of heating is used to melt the ice.
\(\displaystyle a)\) What is the diameter of the wire?
\(\displaystyle b)\) How long does it take to melt the same amount of ice at a temperature of \(\displaystyle -10\,{}^\circ\)C to water at a temperature of \(\displaystyle 0\,{}^\circ\)C?
\(\displaystyle c)\) What is the current in each of the wires?
(4 pont)
solution (in Hungarian), statistics
P. 5183. A coil of inductance \(\displaystyle L\) is connected to the top ends of a vertical pair of rails shown in the figure. The distance between the rails is \(\displaystyle \ell\). A small rod of mass \(\displaystyle m\) and of negligible resistance can move along the rails without friction. The external magnetic field \(\displaystyle \boldsymbol B\) is horizontal and perpendicular to the plane of the rails.
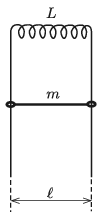
Releasing the rod
\(\displaystyle a)\) at most what is the induced electromotive force in the coil;
\(\displaystyle b)\) and at most what is the induced current?
(5 pont)
solution (in Hungarian), statistics
P. 5184. A high-resolution diffraction grating can deflect a laser beam which enters perpendicularly to the grating, such that the angle of the first order maximum is \(\displaystyle 45^\circ\). What happens if another similar diffraction grating is placed into the path of the diffracted beam such that it is
\(\displaystyle a)\) parallel to the original diffraction grating;
\(\displaystyle b)\) perpendicular to the original diffraction grating?
(The slits of the gratings are parallel to each other in both cases.)
(5 pont)
solution (in Hungarian), statistics
P. 5185. A small disc is moving along a horizontal surface. The resistive force exerted on the disc is proportional to the instantaneous speed of the disc. Two experiments are carried out:
\(\displaystyle (i)\) If the disc is pushed and given an initial speed of \(\displaystyle v_0\), then it moves 50 cm until it stops.
\(\displaystyle (ii)\) When the speed of the initially pushed disc decreases to the value of \(\displaystyle v_0/2\), the disc collides with another initially standing disc. The resistive force exerted on this other disc is also proportional to the speed of this disc. (The proportionality constant is the same for both discs.) The collision is head-on and elastic. Surprisingly, the two discs stop next to each other.
\(\displaystyle a)\) What is the ratio of the masses of the discs?
\(\displaystyle b)\) How far from the position of the collision did the discs stop?
(6 pont)
Upload your solutions above.
