KöMaL Problems in Mathematics, January 2019
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on February 11, 2019. |
K. 609. Given that 50 minutes ago the time past 3 p.m. was four times as many minutes as the time to 6 p.m. (in the same afternoon), what time is it now?
(6 pont)
solution (in Hungarian), statistics
K. 610. We are building a flight of stairs from solid concrete. It leads to a height of 3 metres, and its width is 1 metre. Each step has a height (\(\displaystyle m\)) and a so-called depth (\(\displaystyle l\)), as shown in the figure. It is required that \(\displaystyle 2m+l=64\) cm, and a stair is not allowed to have a height greater than its depth. What is the minimum possible number of steps? How much concrete is needed for the flight of stairs that has the minimum number of steps?
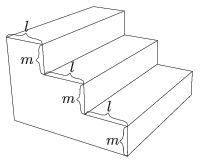
(6 pont)
solution (in Hungarian), statistics
K. 611. Is it possible to arrange the integers 1 to 50 in pairs such that the sums of the numbers in the pairs are all distinct primes?
(6 pont)
solution (in Hungarian), statistics
K. 612. Find all positive integers \(\displaystyle n\) for which \(\displaystyle n + 125\) and \(\displaystyle n + 201\) are perfect squares.
(6 pont)
solution (in Hungarian), statistics
K. 613. Two persons are playing the following game: they take turns in writing positive integers not greater than 10 on a blackboard. A number is not allowed if it is a factor of some number that has been written before. The player who is not able to write a new number on the board will lose the game. Which player has a winning strategy?
Proposed by L. Loránt
(6 pont)
 |
Problems with sign 'C'Deadline expired on February 11, 2019. |
C. 1518. How many \(\displaystyle 13\)-digit positive integers are there which contain only digits of \(\displaystyle 3\), \(\displaystyle 6\), \(\displaystyle 9\), and in which the difference between every pair of consecutive digits is \(\displaystyle 3\)?
(5 pont)
solution (in Hungarian), statistics
C. 1519. The lengths of two sides of a triangle are \(\displaystyle 31\) and \(\displaystyle 22\). The medians drawn to these sides are perpendicular. How long is the third side?
(5 pont)
solution (in Hungarian), statistics
C. 1520. Determine the last two digits of the number \(\displaystyle 2^{2019}+2019^2\).
(5 pont)
solution (in Hungarian), statistics
C. 1521. A circle of half the radius touches a circle of centre \(\displaystyle O\) from the inside at point \(\displaystyle E\). A ray drawn from \(\displaystyle O\) intersects the large circle at \(\displaystyle P\), and the other intersection with the small circle is \(\displaystyle R\). Prove that the arcs \(\displaystyle \widehat{EP}\) and \(\displaystyle \widehat{ER}\) have the same length.
(5 pont)
solution (in Hungarian), statistics
C. 1522. The positive integers are arranged in three rows as follows:
$$\begin{align*} &1 \ \ 4 \ \ 7 \ \ 10 \ \ 13 \ \ 16\ldots\\ &2 \ \ 5 \ \ 8 \ \ 11 \ \ 14 \ \ 17\ldots\\ &3 \ \ 6 \ \ 9 \ \ 12 \ \ 15 \ \ 18\ldots \end{align*}$$Prove that it is possible to select an infinite geometric sequence out of each row.
(5 pont)
solution (in Hungarian), statistics
C. 1523. A convex quadrilateral is divided into triangles by its diagonals. Prove that if there are exactly three different values among the areas of the four triangles then the quadrilateral is a trapezium.
(5 pont)
solution (in Hungarian), statistics
C. 1524. Let \(\displaystyle N\) and \(\displaystyle M\) be positive integers, and let \(\displaystyle p\) and \(\displaystyle q\) denote different primes. Assume that \(\displaystyle N+M\) is a five-digit number, \(\displaystyle N\) is divisible by \(\displaystyle p\) and the number of its divisors is \(\displaystyle q\), while \(\displaystyle M\) is divisible by \(\displaystyle q\) and the number of its divisors is \(\displaystyle p\). Determine all possible values of \(\displaystyle N\) and \(\displaystyle M\).
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 11, 2019. |
B. 4998. A set of small plastic figures used as a visual aid in primary-school mathematics consists of \(\displaystyle 48\) pieces. The figures can be classified according to four different attributes: their size may be large or small, they may have or not have a hole in the middle, their colour may be red, yellow, blue or green, and their shape may be circular, square or triangular. Every possible combination of the four properties (e.g. small, blue circular disc with a hole) occurs exactly once. How many pieces \(\displaystyle x\) are there in the set, such that there exists a piece \(\displaystyle y\) for which the two conditions below both hold?
1. If \(\displaystyle x\) is red or has no hole, then \(\displaystyle y\) is a small yellow square.
2. If \(\displaystyle y\) is small or blue, then \(\displaystyle x\) is a green triangle or some figure without a hole.
Based on a calculus test problem for freshmen at ELTE, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 4999. The incentre of a triangle \(\displaystyle ABC\) is \(\displaystyle O\), the points of tangency on the sides are \(\displaystyle A_1\), \(\displaystyle B_1\), \(\displaystyle C_1\). The points of tangency of the excircles are \(\displaystyle A_2\), \(\displaystyle B_2\), \(\displaystyle C_2\) as shown in the figure. Show that the area of one of the triangles \(\displaystyle OA_1 A_2\), \(\displaystyle OB_1 B_2\) and \(\displaystyle OC_1 C_2\) equals the sum of the areas of the other two triangles.
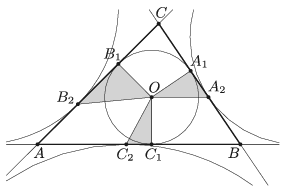
Proposed by: Sz. Kocsis, Budapest
(3 pont)
solution (in Hungarian), statistics
B. 5000. One of \(\displaystyle 4999\) distinct given integers is \(\displaystyle 42\). Prove that it is possible to select some numbers such that their sum is divisible by \(\displaystyle 5000\).
(4 pont)
solution (in Hungarian), statistics
B. 5001. The base of an isosceles triangle is \(\displaystyle a\), its apex angle is smaller than \(\displaystyle 120^{\circ}\), and the altitude drawn to the base is \(\displaystyle m\). Each vertex of the triangle is reflected in the line of the opposite side. The three reflections form a new isosceles triangle, with a base \(\displaystyle a'\) and an altitude \(\displaystyle m'\) drawn to the base. Show that
\(\displaystyle \frac{a'}{a}+\frac{m'}{m}=4.\)
Proposed by P. Bártfai, Budapest
(3 pont)
solution (in Hungarian), statistics
B. 5002. The graph of the cubic polynomial \(\displaystyle x^3 +a x^2 + bx + c\) and the circle of radius \(\displaystyle 10\) centred at the origin intersect at six distinct points \(\displaystyle P_1\), \(\displaystyle P_2\), \(\displaystyle P_3\), \(\displaystyle P_4\), \(\displaystyle P_5\), \(\displaystyle P_6\). Express the centre of mass of the system \(\displaystyle P_1\), \(\displaystyle P_2\), \(\displaystyle P_3\), \(\displaystyle P_4\), \(\displaystyle P_5\), \(\displaystyle P_6\) in terms of the coefficients \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\).
(5 pont)
solution (in Hungarian), statistics
B. 5003. Is it true that if five out of the midpoints of the six edges of a tetrahedron lie on the same sphere, then the sixth midpoint also lies on that sphere?
(5 pont)
solution (in Hungarian), statistics
B. 5004. In a set of \(\displaystyle 2n\) consecutive integers, what is the maximum possible number of elements that are divisible by at least one of the numbers \(\displaystyle n+1\), \(\displaystyle n+2\), \(\displaystyle \ldots\), \(\displaystyle 2n\)?
Proposed by S. Róka, Nyíregyháza
(6 pont)
solution (in Hungarian), statistics
B. 5005. The feet of the altitudes of an acute-angled triangle \(\displaystyle ABC\) drawn to the sides \(\displaystyle BC\), \(\displaystyle CA\), \(\displaystyle AB\) are \(\displaystyle D\), \(\displaystyle E\), \(\displaystyle F\), respectively. The orthocentre of triangle \(\displaystyle ABC\) is \(\displaystyle M\). Let \(\displaystyle k_1\) denote the circle of diameter \(\displaystyle AB\), and let \(\displaystyle k_2\) be the circumscribed circle of triangle \(\displaystyle DEM\). Let \(\displaystyle P\) be an interior point of the arc \(\displaystyle EM\) of \(\displaystyle k_2\) that does not contain point \(\displaystyle D\). Let line \(\displaystyle DP\) intersect circle \(\displaystyle k_1\) again at point \(\displaystyle Q\), and let the midpoint of line segment \(\displaystyle PQ\) be \(\displaystyle R\). Show that lines \(\displaystyle AQ\), \(\displaystyle MP\), \(\displaystyle FR\) are concurrent.
Proposed by B. Bíró, Eger
(6 pont)
 |
Problems with sign 'A'Deadline expired on February 11, 2019. |
A. 740. A \(\displaystyle k\times k\) array contains each of the numbers \(\displaystyle 1,2,\ldots,m\) exactly once, with the remaining entries all zero. Suppose that all the row sums and column sums are equal. What is the smallest possible value of \(\displaystyle m\) if \(\displaystyle k=3^n\) (\(\displaystyle n\in\mathbb{N^+}\))?
Proposed by: Attila Sztranyák and Péter Erben,
based on a problem of the 2017 Kalmár competition
(7 pont)
A. 741. Let \(\displaystyle f\) be a function defined on the positive integers with \(\displaystyle f(n)\ge 0\) and \(\displaystyle f(n)\le f(n+1)\) for all \(\displaystyle n\). Prove that if
\(\displaystyle \sum\limits_{n=1}^\infty \frac{f(n)}{n^2}\)
diverges, there exists a sequence \(\displaystyle a_1,a_2,\dots\) such that the sequence \(\displaystyle \frac{a_n}{n}\) hits every rational number, while
\(\displaystyle a_{n+m}\le a_n+a_m+f(n+m)\)
holds for every pair \(\displaystyle n\), \(\displaystyle m\).
Based on a problem of the Miklós Schweitzer competition
(7 pont)
solution (in Hungarian), statistics
A. 742. Convex quadrilateral \(\displaystyle ABCD\) is inscribed in circle \(\displaystyle \Omega\). Its sides \(\displaystyle AD\) and \(\displaystyle BC\) intersect at point \(\displaystyle E\). Let \(\displaystyle M\) and \(\displaystyle N\) be the midpoints of the circle arcs \(\displaystyle AB\) and \(\displaystyle CD\) not containing the other vertices, and let \(\displaystyle I\), \(\displaystyle J\), \(\displaystyle K\), \(\displaystyle L\) denote the incentres of triangles \(\displaystyle ABD\), \(\displaystyle ABC\), \(\displaystyle BCD\), \(\displaystyle CDA\), respectively. Suppose \(\displaystyle \Omega\) intersects circles \(\displaystyle IJM\) and \(\displaystyle KLN\) for the second time at points \(\displaystyle U\ne M\) and \(\displaystyle V\ne N\). Show that the points \(\displaystyle E\), \(\displaystyle U\), and \(\displaystyle V\) are collinear.
(7 pont)
Upload your solutions above.
