| [295] SAMBUCA | 2005-09-12 00:34:20 |
 Sziasztok!
A titu lemmáról jut eszembe: Csak nem adja be az olimpiai 3. feladatot?! Dehogynem:
xzy 1 és az kell, hogy 1 és az kell, hogy 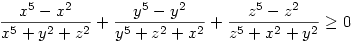 . Első lépésként átalakítunk: x5-x2 helyére: x5+y2+z2-(x2+y2+z2), így az első tört: . Első lépésként átalakítunk: x5-x2 helyére: x5+y2+z2-(x2+y2+z2), így az első tört: 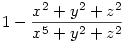 hasonlóan a másik kettő, igy azt kell belátni, hogy: hasonlóan a másik kettő, igy azt kell belátni, hogy: 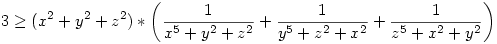 És most jön a trükk: szorozzunk be (x2+y2+z2)-tel! És most jön a trükk: szorozzunk be (x2+y2+z2)-tel!
A baloldalon 3*(x2+y2+z2) lesz, a jobboldalon: 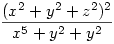 alakú tagok lesznek, amiket Titu-val tudunk felülről becsülni: alakú tagok lesznek, amiket Titu-val tudunk felülről becsülni: 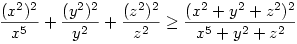 azaz azaz 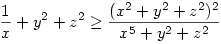 hasonlóan a másik két törtre, ezeket összegezve: hasonlóan a másik két törtre, ezeket összegezve: 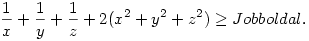 Elég lenne belátni, hogy Elég lenne belátni, hogy 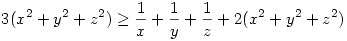 azaz, hogy azaz, hogy 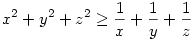 . Nemes egyszerüséggel felszorzunk,igy az kell, hogy: xyz(x2+y2+z2) . Nemes egyszerüséggel felszorzunk,igy az kell, hogy: xyz(x2+y2+z2) xy+yz+zx, ez pedig xyz xy+yz+zx, ez pedig xyz 1 és a rendezési tétel miatt igaz. 1 és a rendezési tétel miatt igaz.
QED
SAMBUCA
|
|
| [294] Kemény Legény | 2005-09-09 10:44:10 |
 A megoldás a 'Titu-lemma' használatával kicsit egyszerűbben is kijön: könnyen ellenőrizhető (pl.felszorzással és négyzetté alakitással),hogy ha x,y,z pozitivak
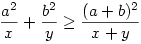
Innen pedig rögtön adódik több tagra is hogy pl.
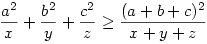
A konkrét esetben pedig
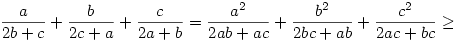
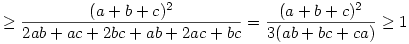 ,ez pedig már nyilvánvaló. ,ez pedig már nyilvánvaló.
A megoldás előnye hogy tetszőlegesen sok tagra általánositható pl.
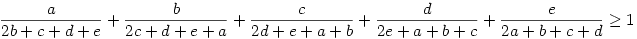
|
| Előzmény: [291] Csimby, 2005-09-05 21:25:00 |
|
| [293] Csimby | 2005-09-07 15:35:15 |
 És akkor a folytatás (sajnos nem találtam egyszerűbbet mint felszorozni mindkét oldalt a bal oldalon lévő nevezőkkel):
a(2c+a)(2a+b)+b(2b+c)(2a+b)+c(2b+c)(2c+a) (2b+c)(2c+a)(2a+b) (2b+c)(2c+a)(2a+b)
2a3+a2b+4ab2+2b3+4a2c+6abc+b2c+ac2+4bc2+2c3 4a2b+2ab2+2a2c+9abc+4b2c+4ac2+2bc2 4a2b+2ab2+2a2c+9abc+4b2c+4ac2+2bc2
2a3+2ab2+2b3+2a2c+2bc2+2c3 3a2b+3abc+3b2c+3ac2 3a2b+3abc+3b2c+3ac2
Számtani és mértani közép közti egyenlőtlenséggel könnyen bizonyítható, hogy:
ab2+a2c+bc2 3abc 3abc
A rendezési tétel miatt:
a3+b3+c3 a2b+b2c+ac2 a2b+b2c+ac2
Már csak ezt a 3 egyenlőtlenséget kell belátnunk:
a(a2+b2) 2a2b 2a2b
b(b2+c2) 2b2c 2b2c
c(c2+a2) 2ac2 2ac2
Az első egyenlőtlenségben a-val, másodikban b-vel, harmadikban c-vel leosztva szintén a számtani és mértani középpel játszva bizonyítható állításokat kapunk.
A közepeket tényleg mindenütt alkalmaztuk, hiszen a,b és c is 2-2 négyzetszám összege, vagyis nem negatív.
Egyenlőség akkor lehet, amikor a közepekben és a rendezési tételben is egyenlőség van, vagyis ha a=b=c. Ekkor x2+y2=y2+z2=x2+z2, vagyis x2=y2=z2.
|
| Előzmény: [291] Csimby, 2005-09-05 21:25:00 |
|
| [292] Lóczi Lajos | 2005-09-05 22:35:40 |
 Vagy (gömbi koordináták helyett): a változószám úgy is csökkenthető, ha mindhárom törtet végigegyszerűsítjük pl. y2-tel: ekkor két új (hányadosokat tartalmazó) változóra átírható az egész. (Hátránya a gömbi koordinátákhoz képest, hogy a változók értelmezési tartományai a pozitív számok lesznek, tehát nem korlátos halmaz. Végigszámolva ebben a konkrét példában azonban egyszerűbb kétváltozós polinomhoz vezet ez a helyettesítés: a rezultánsegyenletnek csak 1 pozitív gyöke van.)
|
| Előzmény: [290] Lóczi Lajos, 2005-09-01 16:23:34 |
|
|
| [290] Lóczi Lajos | 2005-09-01 16:23:34 |
 Az alábbi, egy lehetséges megoldás nyilván nem a legrövidebb, de viszonylag általános eszközöket használ, ezért beírom.
Mivel csupa négyzetes tagok szerepelnek, az az ötletem támadt, hogy térbeli polárkoordinátákat (azaz gömbi koordinátákat) alkalmazzak:
x=r.cos  .cos .cos  , y=r.sin , y=r.sin  .cos .cos  , z=r.sin , z=r.sin  , ,
ahol r>0 (r=0 nyilván nem lehet a nevezők miatt),   [0,2 [0,2 ] a forgásszög, ] a forgásszög,   [- [- /2, /2, /2] pedig az emelkedési szög. /2] pedig az emelkedési szög.
A bizonyítandó
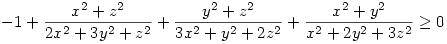
egyenlőtlenségben elvégezve ezeket a helyettesítéseket r kiesik, és csak két változónk marad!
A közös nevezőre hozás után kapunk egy törtet, aminek a nevezője három pozitív szám szorzata, elég tehát a számlálót nézni. Ez nem lesz más, mint
g(A,B):=3-11B+5AB+16B2-28AB2+13A2B2-5B3+12AB3+3A2B3-5A3B3,
ahol az A:=cos2 , B:=cos2 , B:=cos2 rövidítéseket használtam. (A szinuszokat a Pitagorasz-tétellel koszinuszokká konvertáltam.) rövidítéseket használtam. (A szinuszokat a Pitagorasz-tétellel koszinuszokká konvertáltam.)
A továbbiakban elegendő tehát megmutatni, hogy g(A,B) 0 a [0,1]×[0,1] egységnégyzeten, és megnézni, hol állhat egyenlőség. 0 a [0,1]×[0,1] egységnégyzeten, és megnézni, hol állhat egyenlőség.
Most standard szélsőértékszámítást használtam. Könnyű ellenőrizni, hogy g(A,0), g(A,1), g(0,B) és g(1,B) valamennyien pozitívak, ha A,B [0,1]. A peremen tehát stimmel a dolog, csak "belül" kell vizsgálódni. [0,1]. A peremen tehát stimmel a dolog, csak "belül" kell vizsgálódni.
Keressük meg a szokásos módon g lokális szélsőértékeit. Ez egy kis számolás. A derivált(vektor)nak kell megkeresni a zérushelyeit az egységnégyzeten belül (az alsó index jelöli a parciális deriválást): fenn kell álljon, hogy (*)
gA(A,B)=5B-28B2+26AB2+12B3+6AB3-15A2B3=0
gB(A,B)=-11+5A+32B-56AB+26A2B-15B2+36AB2+9A2B2-15A3B2=0
egyszerre nullák. Mivel egy (polinom)egyenletrendszernek csak ott lehetnek megoldásai, ahol a rezultáns nulla, vettem a fenti két egyenlet B-szerinti rezultánsát. Ez A-ban az alábbi ötödfokú egyenlet lett (rögtön faktorizálva egy kicsit):
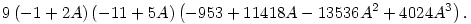
Ennek a gyökei között vannak a lehetséges A-értékek, amelyek (*) megoldásait adják. Nem nehéz kiszűrni, hogy a fenti egyenletnek [0,1]-ben csak A=1/2-nél van gyöke, illetve van még egy gyök az A [9/100,1/10] intervallumban is. Zárjuk ki ez utóbbit. [9/100,1/10] intervallumban is. Zárjuk ki ez utóbbit.
Elemien meggondolható, hogy a B gB(A,B) függvény monoton nő [0,1]-en tetszőleges A gB(A,B) függvény monoton nő [0,1]-en tetszőleges A [9/100,1/10] esetén. Mivel azonban g(A,4/10) minden A [9/100,1/10] esetén. Mivel azonban g(A,4/10) minden A [9/100,1/10] esetén negatív, ezért gB(A,B)<0, ha A [9/100,1/10] esetén negatív, ezért gB(A,B)<0, ha A [9/100,1/10] és B [9/100,1/10] és B [0,4/10]. A másik egyenletről hasonlóan bebizonyítható, hogy gA(A,B)<0, ha A [0,4/10]. A másik egyenletről hasonlóan bebizonyítható, hogy gA(A,B)<0, ha A [9/100,1/10] és B [9/100,1/10] és B [4/10,1]. Ezekből az következik, hogy a (*) egyenletRENDSZERnek nincs megoldása, ha A [4/10,1]. Ezekből az következik, hogy a (*) egyenletRENDSZERnek nincs megoldása, ha A [9/100,1/10] és B [9/100,1/10] és B [0,1]. [0,1].
Marad tehát az A=1/2 egyetlen lehetséges megoldása (*)-nak. Ez pedig valóban jó, amint azt B=2/3 mutatja.
Ott tartunk, hogy az egységnégyzet belsejében a g kétváltozós függvénynek csak (A,B)=(1/2,2/3)-nál LEHET szélsőértéke. A szokásos, Hesse-mátrixos másodrendű elégséges feltétellel azonban meggyőződhetünk róla, hogy itt valóban szélsőérték is VAN, mégpedig lokális minimum.
Meglepő, hogy ez éppen zérushely is: g(1/2,2/3)=0.
A feladat eredeti állítását tehát bebizonyítottuk, és ebből az egyenlőség esete is könnyen látható: a megadott A és B értékekből a  és és  szögek visszaszámolhatók. Ezekből az eredeti x,y és z változókra azt kapjuk, hogy x= szögek visszaszámolhatók. Ezekből az eredeti x,y és z változókra azt kapjuk, hogy x= y (hiszen cos2( y (hiszen cos2( /4)=sin2( /4)=sin2( /4)=1/2), sőt, azt is, hogy x= /4)=1/2), sőt, azt is, hogy x= z (y előjelétől függetlenül), ami pedig azon múlik, hogy z (y előjelétől függetlenül), ami pedig azon múlik, hogy
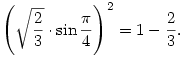
Egyenlőség az eredeti feladatban pontosan akkor van tehát, ha |x|=|y|=|z|.
|
| Előzmény: [289] Suhanc, 2005-08-29 09:37:23 |
|
| [289] Suhanc | 2005-08-29 09:37:23 |
 72.Feladat:
Bizonyítsuk be a megadott egyenlőtlenséget, és vizsgáljuk meg, teljesülhet-e egyenlőség esete!
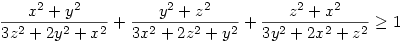
|
|
| [288] Suhanc | 2005-08-29 09:17:54 |
 ...általánosan talán annyit mondhatunk, minden olyan évszámra kizárólag Jonas elképzelése müködőképes, ha a fent leírt szabálynak (evszam-n=j(n)) csak 1 megoldása van, míg, a (evszam-1-n= j(n))-nek legalább egy megoldása van...
|
| Előzmény: [287] Suhanc, 2005-08-29 09:13:04 |
|
| [287] Suhanc | 2005-08-29 09:13:04 |
 Kedves László!
Őszintén szólva Jonas észrevétele után bennem ez a feladat kissé fogásmentessé vált. A konkrét kérdésedre válaszolva, a 2005 szerintem is csak Jonas verziójában működik. Nézzük meg egyenlőre azokat a számokat, melyekre, ha j(n) a szj-ek összege,
2005-n=j(n)
Majd ugyanezt tegyük meg 2004- re is! 2005-re egyetlen példát talált (a gép...:D), amennyiben feltételezzük, hogy 1000 előtt születettek ma már nem élnek. Ez az 1979. Míg 2004-re megfelel 1983 és 2001. Miért kerestünk 2004-re is? Mert az elsőnek elképzelt verzió szerint a feladatnak nem lehet megoldása, hisz egyetlen lehetséges megoldásunk nem lehet azapa és a fiú születési ideje. Ezáltal látszik meg a másik értelmezés pontosító hatása:
Tegyük fel, hogy az év olyan szakaszában vagyunk, amikor a két családtag közül pontosan egyik ünnepelte a születésnapját. (ha még egyik sem ünnepelte, azt nyugodtan tekinthetjük az előző évnek)
Ekkor egyiküknél a 2005-ös képletet kell használnunk, míg a másiknál a 2004-est, hisz ugyanolyan idős, mint 2004-ben, makor betöltötte. Ez alapján már kreálhautnk számpárokat.
Lehetséges pl. hogy az apa 1979-es születésű, míg a fiú 1983 (!!!), avagy az apa 1979,a fiú 2001. Mindkét esetben az apa ünnepelte már a születsnapját.
|
| Előzmény: [285] lorantfy, 2005-07-27 15:37:14 |
|
| [286] [evilcman] | 2005-08-23 18:53:03 |
 71.
p=2 igaz, máskor
* (3;p)=1; (2;p)=1; (6;p)=1
a kis Fermat tételből:
2p-1=pa+1
3p-1=pb+1
6p-1=pc+1
a vizsgált kifejezés így : (3pa + 2pb + pc)/6 egész szám, ugyanakkor * ( (3a + 2b + c)/6 is egész )
|
| Előzmény: [284] Ali, 2005-07-25 09:25:38 |
|
| [285] lorantfy | 2005-07-27 15:37:14 |
 Szia Suhanc!
Kösz, hogy foglalkoztál a feladattal! Gondold át, ha van kedved hozzá, hogy milyen évszámmal kellene megadni a feladatot, hogy csak a Jónás féle verzióban legyen megoldás! (Lehet, hogy 2005 jó lenne?)
Persze más is elgondolkodhat rajta!
|
| Előzmény: [282] Suhanc, 2005-07-12 22:06:32 |
|
| [284] Ali | 2005-07-25 09:25:38 |
 71. feladat.
Ha p 3 prím, akkor 2p-2 + 3p-2 + 6p-2 - 1 osztható p -vel. 3 prím, akkor 2p-2 + 3p-2 + 6p-2 - 1 osztható p -vel.
|
|
| [283] lorantfy | 2005-07-12 22:12:13 |
 Igazad van! A szokás szerint a következő születésnapig az előző életkor számít és ezt a feladat szövege megengedi. Nem erre gondoltam a megfogalmazáskor, de most rájöttem, hogy akkor lenne igazán jó a feladat ha csak egy megoldása lenne, a Te elképzelésed szerinti.
|
| Előzmény: [281] jonas, 2005-07-12 19:46:08 |
|
| [282] Suhanc | 2005-07-12 22:06:32 |
 Kedves László!
Ha nem rontottam el, úgy néz ki, az 1900 és 2000 között születettek közül csak az 1984-re stimmel a feladat állítása (Ha szigorú értelemben vesszük. Jonas elgondolását nem írtam bele a programba). Szóval így kissé meghökkentő a feladat végeredménye...kétszeresen is...
|
| Előzmény: [280] lorantfy, 2005-07-12 18:02:36 |
|
| [281] jonas | 2005-07-12 19:46:08 |
 Miért nem jó az 1979? Ha a szülő mondjuk 1979. októberben született, a gyereke pedig 2002. márciusában, akkor 2006. júliusában a szülő 26 éves, és 1+9+7+9=26, de a gyereke már 4 éves, és 2+0+0+2=4.
|
| Előzmény: [280] lorantfy, 2005-07-12 18:02:36 |
|
|
| [279] jonas | 2005-07-12 15:01:41 |
 Igen, 1979-ben született, a gyermeke pedig 2002-ben. (Nem olyan valószínű, de esetleg az is előfordulhat, hogy 1984-ben született, a gyereke szintén 2002-ben.)
|
| Előzmény: [278] lorantfy, 2005-07-11 12:08:37 |
|
| [278] lorantfy | 2005-07-11 12:08:37 |
 70. feladat: Valaki azt állítja, hogy jövő évben (2006) ő és gyermeke is annyi ídős lesz mint születési évszámuk számjegyeinek összege. Igaza lehet?
|
|
| [277] lorantfy | 2005-04-16 13:54:05 |
 Kedves Suhanc és Fórumosok!
Bizonyítottnak kell tekintenek a gondolatátvitellel való információátadás lehetőségét :-), ugyanis az előző hozzászólásom végére odagondoltam, hogy akkor gyártsatok hasonló feladatokat.
Ezen kívül gratula az 55. feladat megoldásaiért! Nagyon tetszettek.
|
| Előzmény: [276] Suhanc, 2005-04-16 12:21:11 |
|
| [276] Suhanc | 2005-04-16 12:21:11 |
 69.Feladat Bizonyítsd be, hogy:
17|33n+152n+1+25n+111n
|
|
| [275] lorantfy | 2005-04-15 07:50:54 |
 Kedves Csimbi!
Kösz az ügyes és gyors megoldást. Végülis az a lényeg, hogy ha két szám azonos maradékot ad, k-val osztva, akkor n-edik hatványuk is azonos maradékot ad.
|
| Előzmény: [270] Csimby, 2005-04-13 16:48:53 |
|
| [274] Suhanc | 2005-04-14 20:56:45 |
 Kedves Sirpi és Fálesz Mihály!
Köszönöm a megoldásotokat! Igazából már lemondtam róla, hogy bárkit is érdekeljen a feladat... Sirpi, említettél egy közepes megoldást, ami szerintem megegyezik az én megoldásommal. Mindenesetre akkor én azt engedelmeddel "pofátlanul beírnám", szerintem van üzenete...
Megfelelő módon osztjuk részekre a baloldalon lévő mennyiségeket, és ezekből fogjuk a jobb oldal tagjait a számtani- mértani közepek közötti egyenlőtlenség egítségével becsülni.
Eredetileg: a3b+b3c+c3a a2bc+ab2c+abc2 a2bc+ab2c+abc2
Ekkor:
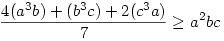
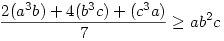
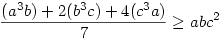
E három egyenlőtlenséget összeadva épp a bizonyítandó állítást kapjuk...
|
| Előzmény: [273] Sirpi, 2005-04-14 14:24:06 |
|
| [273] Sirpi | 2005-04-14 14:24:06 |
 Hát igen, ez jóval egyszerűbb megoldás. Viszont igaz, hogy a másik hosszú, meg számolós, de az enyém :-) Közben rájöttem én is egy másik, nem ennyire számolós megoldásra.
Osszuk le mindkét oldalt abc-vel (ha valamelyik szám 0, akkor triviálisan igaz az egyenlőtlenség):
a2/c+b2/a+c2/b a+b+c a+b+c
Átrendezve:
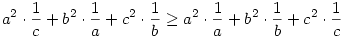
Mindkét oldalon az a2,b2,c2 számok vannak páronként összeszorozva az 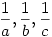 számokkal, és össze vannak adva a szorzatok, csak más sorrendben vannak összepárosítva a két oldalon. Ismert tétel (rendezési tételnek, vagy Szűcs Adolf-tételnek is hívják), hogy egy ilyen szorzat akkor lesz maximális, ha a két összeszorzandó sorozat azonos módon van rendezve, akkor lesz a legkisebb, ha ellentétes módon, ebből következően az összes többi permutáció e kettő közt fog elhelyezkedni. számokkal, és össze vannak adva a szorzatok, csak más sorrendben vannak összepárosítva a két oldalon. Ismert tétel (rendezési tételnek, vagy Szűcs Adolf-tételnek is hívják), hogy egy ilyen szorzat akkor lesz maximális, ha a két összeszorzandó sorozat azonos módon van rendezve, akkor lesz a legkisebb, ha ellentétes módon, ebből következően az összes többi permutáció e kettő közt fog elhelyezkedni.
A jobb oldalon fordított sorrendben van rendezve a két számhármas (ha pl. a2 b2 b2 c2, akkor 1/a c2, akkor 1/a 1/b 1/b 1/c), így a bal oldal legalább akkora, mint a jobb. 1/c), így a bal oldal legalább akkora, mint a jobb.
|
|
| [272] Fálesz Mihály | 2005-04-14 14:03:12 |
 Szia Sirpi,
A megoldást ismertem, ezért nem írtam le eddig. (A 83-as párizsi diákolimpián a legnehezebb feladatot, amire a teljes magyar csapat összesen 1 pontot szerzett, erre az egyenlőtlenségre lehetett visszavezetni egy kis trükkel.)
(a3b+b3c+c3a)-(a2bc+ab2c+abc2)=
=ab(a-c)2+bc(b-a)2+ca(c-b)2 0. 0.
F.M. :-)
|
| Előzmény: [271] Sirpi, 2005-04-14 11:16:40 |
|
| [271] Sirpi | 2005-04-14 11:16:40 |
 Na, akkor a rég eltemetett 55. feladatról írnék, ami úgy szólt, hogy ha a,b,c 0, akkor a3b+b3c+c3a 0, akkor a3b+b3c+c3a a2bc+ab2c+abc2. a2bc+ab2c+abc2.
Kijött közepekkel is, de ha nem akarok nagyágyúkat használni, akkor ki lehet direkt módon is hozni. Első észrevétel, hogy ha a=b=c=0, akkor triviálisan igaz az állítás. Ha meg nem, akkor szorozzunk fel (a+b+c)-vel:
(a+b+c)(a3b+b3c+c3a) abc(a+b+c)2 abc(a+b+c)2
Elvégezve a beszorzást mindkét oldalon 9-9 tagot kapunk, amiből 3 egyezik:
a4b+ab3c+a2c3+a3b2+b4c+abc3+a3bc+b3c2+ac4 a3bc+ab3c+abc3+2a2b2c+2a2bc2+2ab2c2 a3bc+ab3c+abc3+2a2b2c+2a2bc2+2ab2c2
Rendezve:
(a4b+b3c2-2a2b2c)+(b4c+c3a2-2ab2c2)+(c4a+a3b2-2a2bc2) 0 0
Ez pedig nyilvánvalóan igaz, mert ez átírható a következő alakra:
b(a2-bc)2+c(b2-ac)2+a(c2-ab)2 0 0
Egyenlőség akkor áll fenn, ha minden tag 0. Minden tag egy szorzat, ezért az egyenlőségnek az a feltétele, hogy minden tényező valamelyik tagja 0. Nézzük meg az eredeti egyenletet abban az esetben, ha pl. c=0, ekkor a bizony1tandó egyenlet az a3b 0 alakra egyszerűsödik. Vagyis ha van nulla a számok közt, akkor egyenlőség áll fenn, amennyiben van köztük még legalább egy másik nulla is. 0 alakra egyszerűsödik. Vagyis ha van nulla a számok közt, akkor egyenlőség áll fenn, amennyiben van köztük még legalább egy másik nulla is.
Ha nincs nulla a számok közt, akkor pedig az a2=bc,b2=ac,c2=ab egyenlőségek mindegyikének kell teljesülnie, de ha feltesszük, hogy c a legnagyobb, és c2=ab, abból rögtön következik, hogy a=b=c. Tehát az (a,a,a) és az (a,0,0) számpárok esetén van egyenlőség.
|
| Előzmény: [189] Suhanc, 2004-09-22 20:12:09 |
|



 1 és az kell, hogy
1 és az kell, hogy 


 .cos
.cos  , y=r.sin
, y=r.sin  [0,2
[0,2 ] a forgásszög,
] a forgásszög,  gB(A,B) függvény monoton nő [0,1]-en tetszőleges A
gB(A,B) függvény monoton nő [0,1]-en tetszőleges A y (hiszen cos2(
y (hiszen cos2(

 3 prím, akkor 2p-2 + 3p-2 + 6p-2 - 1 osztható p -vel.
3 prím, akkor 2p-2 + 3p-2 + 6p-2 - 1 osztható p -vel.

 1/b
1/b