| [24] Csizmadia Gábor | 2003-12-24 00:54:31 |
 Ugyan nem tudom, hogy ez kinek mennyire nehéz, de szerintem ezek a feladatok megérdemlik, hogy ide kerüljenek, leginkább a C. Az A és a B esetén nem csak konkrét példára gondolok, hanem egy kicsit általánosabb megoldásra.
10. feladat Konstruálj olyan valós-valós (R->R) függvényt (ha létezik ilyen), amely értelmezési tartományának minden nem megszámlálható részhalmazán felveszi a teljes értékkészletet. A. Az értékkészlet ekvivalens N-nel B. Az értékkészlet ekvivalens N-nel, valamint a függvény mindenütt differenciálható C. Az értékkészlet ekvivalens R-rel
|
|
|
|
| [21] Rácz Béla | 2003-12-16 21:52:54 |
 Egy igazi ínyencség, amit egyes érdekes ízlésű emberek diákolimpiára (1,5 óra/feladat) akartak kitűzni:
9. feladat
Mely (f, g) valósokon értelmezett valósértékű függvénypárokra teljesül minden x és y esetén az alábbi egyenlőség?
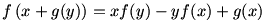
|
|
| [20] Pach Péter Pál | 2003-12-12 19:44:27 |
 Egy újabb feladat:
8. feladat
Legyen  >0. Keressük a legnagyobb >0. Keressük a legnagyobb  számot, amelyre teljesül, hogy ha n elég nagy, akkor megadható ( számot, amelyre teljesül, hogy ha n elég nagy, akkor megadható ( - - )n különböző egész szám 1 és n között úgy, hogy a megadott számok közül egyik sem osztója egy másik kétszeresének. Adjuk meg 1 és n között a lehető legtöbb egész számot ezzel a tulajdonsággal. )n különböző egész szám 1 és n között úgy, hogy a megadott számok közül egyik sem osztója egy másik kétszeresének. Adjuk meg 1 és n között a lehető legtöbb egész számot ezzel a tulajdonsággal.
Megjegyzés:
Félreértések elkerülése végett:  -t nem -t nem  függvényében keressük. függvényében keressük.
|
|
|
| [18] nadorp | 2003-12-12 16:17:28 |
 Kedves Béla !
Most lehet,hogy égni fogok, de közlök egy megoldást a 6. feladatra. Nem tudom elhinni, hogy csak a triviális megoldás létezik ( azaz a sorozat elemei egyenlőek ), de a hibát nem találom. Szóval:
Legyen a p polinom n-ed fokú és írjunk fel egy Euklideszi algoritmushoz hasonlót
p(x)=(x-q2)p1(x)+q1
p1(x)=(x-q3)p2(x)+r2
p2(x)=(x-q4)p3(x)+r3
. . .
pn-2(x)=(x-qn)pn-1(x)+rn-1
Ebből következik, hogy a p polinom alkalmas s2,s3,...sn+1 racionális számokkal felírható a következő alakba:
p(x)=(x-q2)...(x-qn+1)sn+1+(x-q2)...(x-qn)sn+...(x-q2)s2+q1
A fenti eljáráshoz hasonlóan,"eggyel később kezdve",alkalmas t2,t3,...tn+1 számokkal
p(x)=(x-q3)...(x-qn+2)tn+1+(x-q3)...(x-qn+1)tn+...(x-q3)t2+q2
Írjunk a második egyenlőségben x helyére p(x)-et és használjuk fel egyrészt a qi számok közti összefüggést, másrészt, hogy minden polinomban p(x)-p(a)=(x-a)h(x) minden "a" számra. Kapjuk:
p(p(x))=(x-q2)...(x-qn+1)hn+1(x)+(x-q2)...(x-qn)hn(x)+...(x-q2)h2(x)+q1, ahol hi(x) alkalmas racionális együtthatós polinom. Az előzőek alapján
p(p(x))+p(x)=(x-q2)...(x-qn+1)(hn+1(x)+sn+1)+(x-q2)...(x-qn)(hn(x)+sn)+...(x-q2)(h2(x)+s2)+q1+q2
Ha most a fenti egynlőségben x=q3, akkor azt kapjuk, hogy
(q3-q2)(h2(x)+s2)=0
Mivel h2(x) legalább elsőfokú polinom, ez csak úgy lehet, hogy q2=q3.
Teljesen hasonló módszerrel kapjuk, hogy q3=q4 stb. Végül a q3=q2 összefüggésből p(q3)=p(q2), azaz q2=q1 következik.
|
| Előzmény: [16] Rácz Béla, 2003-12-11 00:30:39 |
|
| [17] Rácz Béla | 2003-12-11 19:42:01 |
 Eszembe jutott még egy darab. Nagyon örülnék neki, ha valaki elegáns megoldást adna rá, mert én csak elég kellemetlen bizonyításról tudok. A feladat egy háromszögben a beírt kör középpontjának az Euler-egyeneshez való viszonyát tisztázza:
7. feladat
A beírt kör K középpontjából a súlypontot és a magasságpontot összeköző SM szakasz több, mint 90°-ban látszik; más szóval K benne van az SM átmérőjű körben.
Sőt, ez az állítás éles: ha adottak az S,M,K pontok úgy, hogy ez a feltétel teljesüljön, akkor rajzolható hozzájuk megfelelő háromszög.
|
|
| [16] Rácz Béla | 2003-12-11 00:30:39 |
 Ez a magyar-izraeli versenyen volt pár éve:
6. feladat
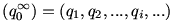 egy végtelen sorozat, ami racionális számokból áll; és p egy legalább másodfokú racionális együtthatós polinom. Tudjuk, hogy p(qi+1)=qi minden lehetséges i-re. egy végtelen sorozat, ami racionális számokból áll; és p egy legalább másodfokú racionális együtthatós polinom. Tudjuk, hogy p(qi+1)=qi minden lehetséges i-re.
Bizonyítandó, hogy a (q) sorozat periodikus.
|
|
| [15] Pach Péter Pál | 2003-12-08 20:40:47 |
 Kedves Péter!
A G gráf egy automorfizmusa: csúcsainak egy  permutációja, amelyre az i és j pontok közötti élek száma megegyezik a permutációja, amelyre az i és j pontok közötti élek száma megegyezik a  (i) és (i) és  (j) pontok közötti élek számával minden (i,j) párra. (j) pontok közötti élek számával minden (i,j) párra.
Részletezve: Megszámozzuk a gráf pontjait 1-től n-ig(, ha n pontja van). Tegyük fel, hogy ezután át tudjuk számozni a gráf pontjait úgy, hogy minden 1 i i j j n esetén teljesül, hogy ha az i. és j. pont között a „régi” számozás mellett futott él, akkor az „új” számozás mellett is fut és ha a „régi” számozás mellett nem futott él, akkor az „új” mellett sem fut. (Amennyiben a gráf nem egyszerű, akkor azt is megköveteljük, hogy ugyanannyi él fusson.) Az „új” számozást (vagyis a gráf pontjainak ezt a permutációját) a gráf egy automorfizmusának nevezzük. Minden gráfnak van legalább egy automorfizmusa: az identitás (amikor minden pont száma változatlan marad). (Általában egy „véletlenszerűen” felrajzolt gráfnak nincs is más automorfizmusa.) n esetén teljesül, hogy ha az i. és j. pont között a „régi” számozás mellett futott él, akkor az „új” számozás mellett is fut és ha a „régi” számozás mellett nem futott él, akkor az „új” mellett sem fut. (Amennyiben a gráf nem egyszerű, akkor azt is megköveteljük, hogy ugyanannyi él fusson.) Az „új” számozást (vagyis a gráf pontjainak ezt a permutációját) a gráf egy automorfizmusának nevezzük. Minden gráfnak van legalább egy automorfizmusa: az identitás (amikor minden pont száma változatlan marad). (Általában egy „véletlenszerűen” felrajzolt gráfnak nincs is más automorfizmusa.)
Példák:
- Az n pontú teljes gráfnak automorfizmusainak száma n!.
- Egy (2<)n hosszú kör automorfizmusainak száma 2n.
- A Petersen-gráf automorfizmusainak száma 120.
Az automorfizmusokat pedig úgy szorozhatjuk össze, hogy összeszorozzuk a hozzájuk tartozó permutációkat. Innen már végig lehet gondolni, hogy valóban csoportot alkotnak…
A példádat egyébként ismerem, úgyhogy Attilára, vagy másra vár a feladat, hogy megoldja, és feltegye a megoldást.
|
| Előzmény: [11] nadorp, 2003-12-08 13:53:55 |
|
| [14] Pach Péter Pál | 2003-12-08 20:29:51 |
 Térjünk vissza a 3. feladathoz, és a [4]-ben feltettem kérdésemhez. A kérdésre a válasz az, hogy nem, és nem csak „ehhez hasonlóan” nem bizonyítható, hanem egyáltalán nem, ugyanis nem is igaz.
A feladat átfogalmazható úgy, hogy 0<y1,y2,…,yn esetén igaz-e, hogy 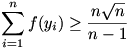 , ha , ha 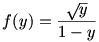 . .
Az f függvény a ![\left[0;\sqrt{\frac43}-1\right]](keplet.cgi?k=D8FAC312033F382D) intervallumon konkáv, a intervallumon konkáv, a 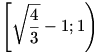 intervallumon pedig konvex. Ezt f’’(x) előjelének vizsgálatával (amihez másodfokú egyenletet kell megoldanunk) állapíthatjuk meg. intervallumon pedig konvex. Ezt f’’(x) előjelének vizsgálatával (amihez másodfokú egyenletet kell megoldanunk) állapíthatjuk meg.
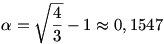
Ha n=3, akkor ha y1,y2,y3 mind legalább  , akkor készen vagyunk a Jensen-egyenlőtlenséggel. Ha közülük egy, vagy kettő , akkor készen vagyunk a Jensen-egyenlőtlenséggel. Ha közülük egy, vagy kettő  -nál kisebb, akkor a többi „annyira nagy” lesz, hogy még erősebb becslést nyerünk. (Ezt viszonylag gyorsan ki lehet hozni.) Viszont, ha n nagy, akkor lehetséges, hogy akár az összes yi kisebb, mint -nál kisebb, akkor a többi „annyira nagy” lesz, hogy még erősebb becslést nyerünk. (Ezt viszonylag gyorsan ki lehet hozni.) Viszont, ha n nagy, akkor lehetséges, hogy akár az összes yi kisebb, mint  , s ilyenkor éppen a Jensen-egyenlőtlenség mutatja, hogy , s ilyenkor éppen a Jensen-egyenlőtlenség mutatja, hogy 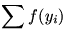 még csökkenthető. (Hiszen a [0; még csökkenthető. (Hiszen a [0; ] intervallumon f konkáv.) ] intervallumon f konkáv.)
|
| Előzmény: [4] Pach Péter Pál, 2003-12-02 23:05:43 |
|
|
|
| [11] nadorp | 2003-12-08 13:53:55 |
 Kedves Attila !
Teljesen igazad van abban, hogy a rendezettségen alapuló egyenlőtlenség nagyon hasznos. Ha érdekel, nézd meg a KÖMAL A.324. sz. példára adott harmadik megoldást, nagyon tanulságosan használja fel ezt az egyenlőtlenséget.
Kedves Péter ! (különben én is az vagyok)
Az első példa kapcsán - valószínűleg anno kihagytam pár absztrakt algebrai előadást - kisebb gondjaim vannak azzal, hogy hogyan értelmezzem egy gráf automorfizmusát ( kétféle leképezést is találtam egy konkrét esetben, így az egyik biztos nem jó). Légy szíves pár szóval vázold. Van egy aranyos példám is. Az 198[3-8] évben tűzték ki a Riesz Frigyes matek versenyen.
4.feladat
Adott egy n-elemű X halmaz ( n 1 pozitív egész ) és adott X-nek n darab különböző ( nem feltétlenül valódi ) részhalmaza A1,A2...An. BBh. létezik x 1 pozitív egész ) és adott X-nek n darab különböző ( nem feltétlenül valódi ) részhalmaza A1,A2...An. BBh. létezik x X , hogy az A1\{x},A2\{x} … An\{x} halmazok is különbözőek. X , hogy az A1\{x},A2\{x} … An\{x} halmazok is különbözőek.
|
|
| [10] jenei.attila | 2003-12-08 10:43:51 |
 Kedves nadorp!
Teljesen igazad van, amikor leírtam, már én is rájöttem. Ahogy említettem is, nem gondoltam végig, csak egy ötlet volt, először jónak tűnt.
A harmadik feladatnál nem kell használni a "skalár szorzatos" (nem tudok rá jobb nevet, és ennyi erővel a Cauchy-Schwartz egyenlőtlenséget is lehetne így nevezni) egyenlőtlenséget, mert a feladathoz elég a
(x-y)2+(x-z)2+(y-z)2 0 0
egyenlőtlenséget átrendezni, azonban a "skalár szorzatos" önmagában is érdekes és sokszor nagyon hasznos egyenlőtlenség.
|
|
|
| [8] nadorp | 2003-12-08 09:30:10 |
 Kedves Attila !
A 3. feladatra adott ötleted annyiban hibás,hogy a 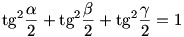 feltételből csak annyi következik, hogy feltételből csak annyi következik, hogy  + + + + <=180o (Jensen egyenlőtlenség), tehát nem biztos, hogy egyáltalán háromszöget kapsz.Pld. próbáld ki a <=180o (Jensen egyenlőtlenség), tehát nem biztos, hogy egyáltalán háromszöget kapsz.Pld. próbáld ki a 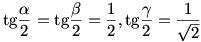 esetet, esetet,  + + + + =176,78o-ot fogsz kapni. =176,78o-ot fogsz kapni.
Egyébként,ha  , , , , egy háromszög szögei, akkor könnyű a bizonyítás, mert a tan egy háromszög szögei, akkor könnyű a bizonyítás, mert a tan  +tan +tan  +tan +tan  =tan =tan  tan tan  tan tan  azonosság miatt, felhasználva a számtani és mértani közép közötti összefüggést: azonosság miatt, felhasználva a számtani és mértani közép közötti összefüggést:
(tan  +tan +tan  +tan +tan  )3>=27tan )3>=27tan  tan tan  tan tan  =27(tan =27(tan  +tan +tan  +tan +tan  ), ezért ), ezért
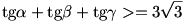
|
| Előzmény: [7] jenei.attila, 2003-12-07 23:00:44 |
|
| [7] jenei.attila | 2003-12-07 23:00:44 |
 Kedves Péter!
A negyedik feladat megoldásával is megelőzött nadorp, azért leírom az enyémet:
A megoldás során két jól ismert egyenlőtlenséget fogunk felhasználni. Az egyik a hatványközepekre vonatkozó egyenlőtlenség, amely szerint ha    , akkor nem negatív számok , akkor nem negatív számok  -adik hatványközepe nem nagyobb a -adik hatványközepe nem nagyobb a  -adik hatványközepüknél. x,y,z négyzetes és köbös hatványközepére: -adik hatványközepüknél. x,y,z négyzetes és köbös hatványközepére:
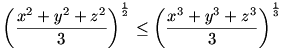
Mindkét oldalt 6-odik hatványra emelve, és 8/9 -del beszorozva kapjuk:
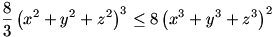
A másik egyenlőtlenség két számsorozat "skaláris szorzatára" vonatkozik, amely szerint az akkor maximális, ha a sorozatok egyezőleg rendezettek, minimális, ha ellenkezőleg rendezettek. Például x,y,z -re
xy+yz+zx x2+y2+z2 x2+y2+z2
A bizonyítandó egyenlőtlenség bal oldalának zárójeles kifejezéseire alkalmazva a számtani-mértani közép egyenlőtlenségét majd köbre emelve és 9-cel beszorozva:
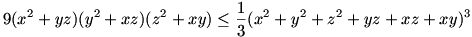
Ebben az egyenlőtlenségben a jobboldal (a "skalár szorzatos" egyenlőtlenség miatt):
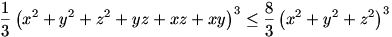
A két utóbbi és a hatványközepekre vonatkozó egyenlőtlenséget összevetve kapjuk a bizonyítandó állítást:
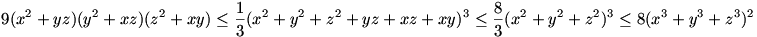
A 3. feladat megoldását nem gondoltam végig, mert nadorp megoldása egyszerűbb, azért ezt is leírom. Az 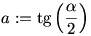 helyettesítést bevezetve a bizonyítandó egyenlőtlenség helyettesítést bevezetve a bizonyítandó egyenlőtlenség 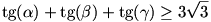 . A feltételek . A feltételek  , , , , hegyesszögű háromszöget adnak meg. hegyesszögű háromszöget adnak meg.
|
| Előzmény: [2] Pach Péter Pál, 2003-12-01 22:09:03 |
|
| [6] Pach Péter Pál | 2003-12-04 22:32:09 |
 Kedves Péter! (Csak tippeltem, ha tévedek, javíts ki!)
Köszi a megoldást a 4. feladatra. A 3. feladatnál szerintem azért nem zavaró a 2-es szorzó elhagyása, mert az egyenlet 0-ra volt rendezve. A [4]-ben feltett kérdésemen nagyon sokat nem érdemes töprengeni, ugyanis kicsit becsapós. :-) Nos?
Sok sikert az első két feladathoz!
|
| Előzmény: [5] nadorp, 2003-12-04 14:12:26 |
|
| [5] nadorp | 2003-12-04 14:12:26 |
 Kedves Péter !
A 3. feladatra adott megoldás nem annyira remek, mert egyrészt elhagytam a nevezőben egy 2-es szorzót ( bár ez a lényegen nem változtat), másrészt nem általánosítható n>3 esetére, mert ekkor 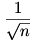 csak egyszeres gyök, ezért nem a négyzeten szerepel a szorzatban. Azért még küzdök vele.Viszont van egy megoldásom a 4. feladatra. csak egyszeres gyök, ezért nem a négyzeten szerepel a szorzatban. Azért még küzdök vele.Viszont van egy megoldásom a 4. feladatra.
Elég bizonyítani, hogy
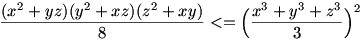
Vonjunk mindkét oldalból 6-ik gyököt. Ekkor
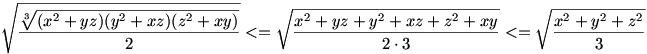
Felhasználva hogy a 2-dik hatványközép kisebb egyenlő a 3-dik hatványközépnél, a bizonyítandó állítást kapjuk
|
| Előzmény: [2] Pach Péter Pál, 2003-12-01 22:09:03 |
|
|
| [3] nadorp | 2003-12-02 17:11:35 |
 Megoldás a 3. feladatra.
Az ember a szimmetria miatt akaratlanul arra gondol, egyenlőség csak 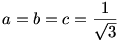 esetén van. Ekkor a balodalon álló összes tört értéke esetén van. Ekkor a balodalon álló összes tört értéke 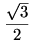 . Másrészt . Másrészt 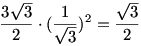 is teljesül, ezért az is teljesül, ezért az
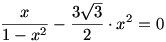
egyenletnek az 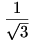 szám gyöke,ezért belőle a szám gyöke,ezért belőle a 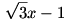 kifejezés kiemelhető. Valóban, nem részletezve a számolást, a fenti egyenlet bal oldalára a következőt kapjuk: kifejezés kiemelhető. Valóban, nem részletezve a számolást, a fenti egyenlet bal oldalára a következőt kapjuk:
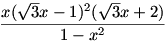 , ami a (0;1) nyílt intervallumon nemnegatív. , ami a (0;1) nyílt intervallumon nemnegatív.
Most már az eredeti feladat könnyen megoldható. A fenti egyenelet bal oldalán szereplő kifejezésbe helyettesítsük rendre az a,b és c számokat és adjuk össze ezt a három kifejezést. Felhasználva a négyzetösszegekre vonatkozó feltételt, pont a kívánt egyenlőtlenséget kapjuk.
|
| Előzmény: [2] Pach Péter Pál, 2003-12-01 22:09:03 |
|
| [2] Pach Péter Pál | 2003-12-01 22:09:03 |
 A továbbiakban „Bizonyítsuk be, hogy” röviden „Bbh” lesz. Kezdetnek négy feladat: (Kedvcsinálónak könnyebb példa is van köztük. :-))
1. feladat: Bbh bármely véges csoporthoz létezik olyan véges egyszerű gráf, amelynek az automorfizmuscsoportja izomorf vele.
2. feladat: Bbh egy gráfban akkor és csak akkor létezik teljes párosítás, ha akárhogyan is hagyunk el néhány pontot (és a belőlük kiinduló éleket), a maradékban a páratlan komponensek száma nem nagyobb az elhagyott pontok számánál. Megjegyzés: bocs mindenkitől, aki ismeri.
3. feladat: 0<a,b,c<1 és a2+b2+c2=1. Bbh
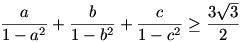
4. feladat: x,y,z nemnegatívak, bbh
9(x2+yz)(y2+zx)(z2+xy) 8(x3+y3+z3)2 8(x3+y3+z3)2
|
|
| [1] Pach Péter Pál | 2003-12-01 22:04:53 |
 Azért nyitottam ezt a témát, hogy a nehezebb példákat is kitűzhessük valahol. Tehát itt olyan feladatokat adnánk fel és oldanánk meg, amiket nem írunk be az Érdekes matekfeladatok-hoz, mert nehéznek érezzük őket. Természetesen kevésbé nehéz példákat is kitűzhetünk, senki se tartson vissza példát csupán azért, mert aggódik, hogy az nem elég kemény.
|
|





 >0. Keressük a legnagyobb
>0. Keressük a legnagyobb  számot, amelyre teljesül, hogy ha n elég nagy, akkor megadható (
számot, amelyre teljesül, hogy ha n elég nagy, akkor megadható ( permutációja, amelyre az i és j pontok közötti élek száma megegyezik a
permutációja, amelyre az i és j pontok közötti élek száma megegyezik a  i
i ,
, egy háromszög szögei. Ebből a rendezési tétel (amit „skalár szorzatos egyenlőtlenség”-nek hívtál) alapján látszik, hogy 1
egy háromszög szögei. Ebből a rendezési tétel (amit „skalár szorzatos egyenlőtlenség”-nek hívtál) alapján látszik, hogy 1 1 pozitív egész ) és adott X-nek n darab különböző ( nem feltétlenül valódi ) részhalmaza A1,A2...An. BBh. létezik x
1 pozitív egész ) és adott X-nek n darab különböző ( nem feltétlenül valódi ) részhalmaza A1,A2...An. BBh. létezik x X , hogy az A1\{x},A2\{x} … An\{x} halmazok is különbözőek.
X , hogy az A1\{x},A2\{x} … An\{x} halmazok is különbözőek.