KöMaL Problems in Mathematics, November 2017
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on December 11, 2017. |
K. 559. How many at most six-digit numbers are there in which each of the digits 1, 2, 3, 4, 5 occurs exactly once?
(6 pont)
solution (in Hungarian), statistics
K. 560. There were 30 candidates taking an exam. The average score of those who failed was 60, and the average score of those who passed was 84. The average score of all candidates was 80. How many of them passed the exam?
(6 pont)
solution (in Hungarian), statistics
K. 561. A novel was published in three volumes. The page numbering started with 1 in the first volume, and in the second and third volumes it continued where the previous volume ended. The second volume was 50 pages thicker than the first one, and the third volume was 1.5 times as thick as the second volume. The sum of the first page numbers in the three volumes was 893. How many pages long is the entire novel? How many digits were used altogether in numbering the pages?
(6 pont)
solution (in Hungarian), statistics
K. 562. Alice went shopping. She only had 10-forint coins (HUF, Hungarian currency) and 1000-forint notes on her, at least one of each. When she had spent half her money, she noticed that she only had 10-forint coins and 1000-forint notes again. She had as many 10-forint coins as the number of 1000-forint notes she had set out with, and she had half as many 1000-forint notes as the initial number of her 10-forint coins. Given that she had spent the least amount of money that meets the given conditions, how many forints had she spent?
(6 pont)
solution (in Hungarian), statistics
K. 563. A disc of radius 3 cm has been cut out of each corner of a square plate of side 18 cm as shown in the figure. The small pieces falling off at the corners were thrown away. What is the area of the remaining part of the plate?
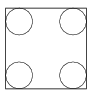
(6 pont)
solution (in Hungarian), statistics
K. 564. A spider wears 8 identical socks and 8 identical shoes on its feet. (There needs to be a sock and a shoe on every foot.) In how many different orders may the spider put on his socks and shoes in the morning, provided that for any given foot, the sock needs to be put on before the shoe, but not necessarily directly before that. (Two orders are only distinguished by the order of the feet.)
(6 pont)
 |
Problems with sign 'C'Deadline expired on December 11, 2017. |
C. 1441. A coffee shop serves coffee specials made from various ingredients. For any item selected from the menu there exist exactly three others that each have some ingredient in common with the selected item. If two menu items have no ingredient in common then there exists a third one that has an ingredient in common with each of the two. What is the maximum possible number of items on the menu of cofee specials?
(5 pont)
solution (in Hungarian), statistics
C. 1442. The sides \(\displaystyle a\), \(\displaystyle b\) and \(\displaystyle c\) of a triangle satisfy
\(\displaystyle 1=\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}. \)
Prove that \(\displaystyle r\cdot R=\frac 12\), where \(\displaystyle r\) is the inradius and \(\displaystyle R\) is the circumradius.
Proposed by Zs. M. Tatár, Felsőgöd
(5 pont)
solution (in Hungarian), statistics
C. 1443. In how many different ways is it possible to represent \(\displaystyle 2017^3\) as a sum of consecutive positive odd numbers?
Based on the idea of L. Hommer, Kemence
(5 pont)
solution (in Hungarian), statistics
C. 1444. Solve the following inequality:
\(\displaystyle x^4-4x^3+8x^2-8x\le 96. \)
(5 pont)
solution (in Hungarian), statistics
C. 1445. The movie ``The Englishman Who Went up a Hill but Came down a Mountain'' is set in a Welsh village where the neighbouring mountain was designated as a hill by cartographers measuring its height. The villagers were too proud of their mountain to accept this. So they decided to raise its height from 984 feet to 1004 feet. They would carry earth onto the the hilltop shaped like a hemisphere of radius 82 feet, to build a truncated cone with its side tangent to the hemisphere and forming a \(\displaystyle 45^\circ\) angle with the horizontal (see the figure). Thus the height will exceed 1000 feet and the hill would qualify to be called a mountain. How many cubic feet of earth need to be carried onto the hilltop?
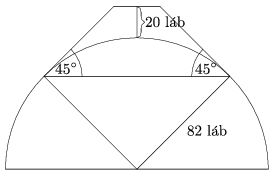
(5 pont)
solution (in Hungarian), statistics
C. 1446. \(\displaystyle Q\) is a point inside the parallelogram \(\displaystyle ABCD\) such that \(\displaystyle \angle AQB +\angle CQD =180^{\circ}\). Prove that \(\displaystyle \angle QBA= \angle QDA\) and \(\displaystyle \angle QAD =\angle QCD\).
(5 pont)
solution (in Hungarian), statistics
C. 1447. The Hungarian term for probability theory is ``valószínűség-számítás''. What is the probability that by selecting and writing down two random characters from each of the words VALÓSZÍNŰSÉG, and SZÁMÍTÁS, the same two-letter string is obtained in both cases?
(5 pont)
 |
Problems with sign 'B'Deadline expired on December 11, 2017. |
B. 4903. Determine all positive integers \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle d\) such that \(\displaystyle abcd-1\mid a+b+c+d\).
Proposed by J. Szoldatics, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 4904. A plane figure \(\displaystyle S\) has exactly two axes of symmetry. Show that \(\displaystyle S\) has central symmetry, too.
(3 pont)
solution (in Hungarian), statistics
B. 4905. Let \(\displaystyle a_1 \ge a_2 \ge a_3 \ge \cdots \ge a_{2n-1} \ge a_{2n} \ge 0\), and \(\displaystyle \sum_{i=1}^{2n} a_i = 1\). Prove that
\(\displaystyle a_1 a_2 + 3 a_3 a_4 + 5 a_5 a_6 + \ldots + (2n-1) a_{2n-1} a_{2n} \le \frac{1}{4}. \)
When will the equality hold?
(4 pont)
solution (in Hungarian), statistics
B. 4906. The midpoints of sides \(\displaystyle BC\) and \(\displaystyle CD\) of a convex quadrilateral \(\displaystyle ABCD\) are \(\displaystyle E\) and \(\displaystyle F\), respectively. The line segments \(\displaystyle AE\), \(\displaystyle EF\) and \(\displaystyle AF\) divide the quadrilateral into four triangles whose areas are four consecutive integers. What is the maximum possible area of triangle \(\displaystyle ABD\)?
Proposed by S. Róka, Nyíregyháza
(5 pont)
solution (in Hungarian), statistics
B. 4907. \(\displaystyle 1\times 1\) squares are placed on a rectangle of dimensions \(\displaystyle a\times b\), with sides parallel to the sides of the rectangle. Prove that the maximum number of such squares without overlaps is \(\displaystyle [a] \cdot [b]\) (where \(\displaystyle [x]\) stands for the greatest integer not greater than the number \(\displaystyle x\)).
(5 pont)
solution (in Hungarian), statistics
B. 4908. Let \(\displaystyle C\) denote an arbitrary point on the circumference of a circle of diameter \(\displaystyle AB\). Let \(\displaystyle T\) be the perpendicular projection of point \(\displaystyle C\) onto the line segment \(\displaystyle AB\). Draw the circle of centre \(\displaystyle C\) that passes through \(\displaystyle T\). Let the intersections of the two circles be \(\displaystyle P\) and \(\displaystyle Q\). Prove that line \(\displaystyle PQ\) bisects the line segment \(\displaystyle CT\).
(Kvant)
(4 pont)
solution (in Hungarian), statistics
B. 4909. Find all functions \(\displaystyle f\colon \mathbb{R}\to\mathbb{R}\) such that the equation
\(\displaystyle x \cdot f(y) - y \cdot f(x) = f\left(\frac{y}{x}\right). \)
holds for all \(\displaystyle x\ne0\) and \(\displaystyle y\).
(Kvant)
(6 pont)
solution (in Hungarian), statistics
B. 4910. Let \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\) and \(\displaystyle S\) denote points on the lines of the sides of a square \(\displaystyle ABCD\) such that \(\displaystyle AP=BQ=CR=DS\), as shown in the figure. Starting from an arbitrary interior point \(\displaystyle X\) of side \(\displaystyle AB\), let the line \(\displaystyle PX\) intersect line \(\displaystyle BC\) at \(\displaystyle Y\), let \(\displaystyle QY\) intersect line \(\displaystyle CD\) at \(\displaystyle Z\), let \(\displaystyle RZ\) intersect line \(\displaystyle DA\) at \(\displaystyle V\), and finally let \(\displaystyle SV\) intersect line \(\displaystyle AB\) at \(\displaystyle X'\). Prove that if \(\displaystyle X'\) and \(\displaystyle X\) coincide then \(\displaystyle XYZV\) is a square.
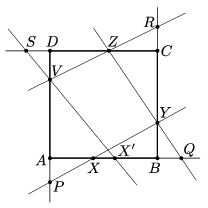
(5 pont)
solution (in Hungarian), statistics
B. 4911. We have placed chessmen on a \(\displaystyle 8\times 8\) chessboard. There is an odd number of chessmen standing in every row, and in every column. Prove that the total number of chessmen on the black fields of the chessboard is even.
(5 pont)
 |
Problems with sign 'A'Deadline expired on December 11, 2017. |
A. 707. \(\displaystyle 100\) betyárs stand on the Hortobágy plains. Every betyár's field of vision is a \(\displaystyle 100\) degree angle. After each of them announces the number of other betyárs they see, we compute the sum of these \(\displaystyle 100\) numbers. What is the largest value this sum can attain?
(5 pont)
solution (in Hungarian), statistics
A. 708. Let \(\displaystyle S\) be a finite set of rational numbers. For each positive integer \(\displaystyle k\), let \(\displaystyle b_k=0\) if we can select \(\displaystyle k\) (not necessarily distinct) numbers in \(\displaystyle S\) whose sum is \(\displaystyle 0\), and \(\displaystyle b_k=1\) otherwise. Prove that the binary number \(\displaystyle 0.b_1b_2b_3\dots\) is a rational number. Would this statement remain true if we allowed \(\displaystyle S\) to be infinite?
(5 pont)
solution (in Hungarian), statistics
A. 709. Let \(\displaystyle a>0\) be a real number. Find the minimal constant \(\displaystyle C_a\) for which the inequality
\(\displaystyle C_a\sum_{k=1}^n \frac1{x_k-x_{k-1}} >\sum_{k=1}^n \frac{k+a}{x_k} \)
holds for any positive integer \(\displaystyle n\) and any sequence \(\displaystyle 0=x_0<x_1<\cdots<x_n\) of real numbers.
(5 pont)
Upload your solutions above.
