KöMaL Problems in Mathematics, April 2019
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'C'Deadline expired on May 10, 2019. |
C. 1539. Let \(\displaystyle E\) denote the point on side \(\displaystyle AB\) of a square \(\displaystyle ABCD\) which divides the side \(\displaystyle 1:3\), with the shorter segment lying closer to \(\displaystyle A\). Let \(\displaystyle F\) be an arbitrary point of diagonal \(\displaystyle BD\). Determine the minimum of the sum \(\displaystyle AF+EF\).
(5 pont)
solution (in Hungarian), statistics
C. 1540. The coefficients of the quadratic expression \(\displaystyle ax^2+bx+c\) are integers, and \(\displaystyle a>0\). It has two distinct positive roots smaller than 1. Find the smallest possible value of \(\displaystyle a\).
(5 pont)
solution (in Hungarian), statistics
C. 1541. Prove that there exists a sequence of 2019 consecutive positive integers that includes exactly 19 primes.
(5 pont)
solution (in Hungarian), statistics
C. 1542. The lengths of the legs in a right-angled triangle \(\displaystyle ABC\) are 5 and 12. Let \(\displaystyle P\), \(\displaystyle Q\) and \(\displaystyle R\) be points on the inscribed circle of the triangle such that triangle \(\displaystyle PQR\) is similar to triangle \(\displaystyle ABC\). Determine the lengths of the sides of triangle \(\displaystyle PQR\).
(5 pont)
solution (in Hungarian), statistics
C. 1543. For what values of the positive integer \(\displaystyle n\) will \(\displaystyle 2^n+1\) or \(\displaystyle 2^n-1\) be divisible by 9?
(5 pont)
solution (in Hungarian), statistics
C. 1544. The diagonals of a circumscribed trapezium \(\displaystyle ABCD\) intersect at \(\displaystyle E\). The radii of the inscribed circles of triangles \(\displaystyle ABE\), \(\displaystyle BCE\), \(\displaystyle CDE\) and \(\displaystyle DAE\) are \(\displaystyle r_1\), \(\displaystyle r_2\), \(\displaystyle r_3\) and \(\displaystyle r_4\), respectively. Prove that
\(\displaystyle \frac{1}{r_1}+\frac{1}{r_3}=\frac{1}{r_2}+\frac{1}{r_4}. \)
(5 pont)
solution (in Hungarian), statistics
C. 1545. Find the real solutions of
$$\begin{align*} x^2-y^2 & =\log_2 \frac yx,\\ 3^{x^2+y^2-1}-4\cdot3^{xy}+9 & =0. \end{align*}$$(Romanian competition problem)
(5 pont)
 |
Problems with sign 'B'Deadline expired on May 10, 2019. |
B. 5022. Given some unit circles on the plane, we coloured each centre blue. On the circumferences of the circles, we marked some points red such that there should be exactly 2 red points on the circumference of each circle. What is the maximum possible number of blue points if there are 25 coloured points altogether?
Proposed by S. Róka, Nyíregyháza
(3 pont)
solution (in Hungarian), statistics
B. 5023. In a triangle \(\displaystyle ABC\), \(\displaystyle \angle ACB=90^{\circ}\) and \(\displaystyle AC>BC\). Let \(\displaystyle X\) be the midpoint of the arc \(\displaystyle AB\) of the circumscribed circle that does not contain \(\displaystyle C\). The perpendicular drawn to \(\displaystyle CX\) at \(\displaystyle X\) intersects line \(\displaystyle CA\) at \(\displaystyle P\). Show that \(\displaystyle AP=BC\).
Proposed by L. Surányi, Budapest
(3 pont)
solution (in Hungarian), statistics
B. 5024. Let \(\displaystyle p\) denote an odd prime. If each of the numbers \(\displaystyle \binom{p-2}{0}, \binom{p-2}{1}, \ldots, \binom{p-2}{p-2}\) are divided by \(\displaystyle p\), how many different remainders are obtained?
Proposed by Z. Gyenes and B. Hujter, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 5025. The inscribed circle of triangle \(\displaystyle ABC\) is centred at \(\displaystyle I\), and touches sides \(\displaystyle BC\), \(\displaystyle CA\) and \(\displaystyle AB\) at points \(\displaystyle D\), \(\displaystyle E\) and \(\displaystyle F\), respectively. Let \(\displaystyle M\) be an arbitrary point in the interior of side \(\displaystyle BC\), different from \(\displaystyle D\). Let the lines \(\displaystyle DI\) and \(\displaystyle EF\) intersect at \(\displaystyle T\), and let \(\displaystyle K\) denote the midpoint of line segment \(\displaystyle MT\). Prove that the circles \(\displaystyle DEF\), \(\displaystyle TDM\) and \(\displaystyle KIT\) are concurrent.
Proposed by M. Agazade, Azerbaijan
(5 pont)
solution (in Hungarian), statistics
B. 5026. Let \(\displaystyle P\) be an arbitrary point of a given ellipse, different from the endpoints of the major axis. \(\displaystyle P\) is connected to the foci \(\displaystyle F_1\) and \(\displaystyle F_2\). The angle bisector of angle \(\displaystyle \angle F_1PF_2\) intersects \(\displaystyle F_1F_2\) at \(\displaystyle E\). The circle which passes through \(\displaystyle P\) and touches \(\displaystyle F_1F_2\) at \(\displaystyle E\) intersects \(\displaystyle PF_1\) at \(\displaystyle G\) and \(\displaystyle PF_2\) at \(\displaystyle H\). Show that the length of \(\displaystyle GH\) does not depend on the choice of \(\displaystyle P\).
Proposed by L. Németh, Fonyód
(4 pont)
solution (in Hungarian), statistics
B. 5027. Arthur Dumpling (Hungarian cartoon character: a fat bird who loves chocolate of all kinds) lives at 1 Sweet Street. The chocolate shop is operating at number \(\displaystyle n\), the far end of the street. Arthur's daily fitness programme is as follows: he starts in front of number 2. When he stands in front of number \(\displaystyle k\) (where \(\displaystyle 1<k<n\)), he tosses a fair chocolate coin. If it shows heads, he moves to number \(\displaystyle (k-1)\). If it shows tails, he moves to number \(\displaystyle (k+1)\). If he reaches the chocolate shop, he enters and throws a chocolate ball down his throat, and then moves to number \(\displaystyle (n-1)\). If he arrives back home, the fitness programme terminates. On average, how many chocolate balls does Arthur throw down his throat per day?
(5 pont)
solution (in Hungarian), statistics
B. 5028. Let us define a function \(\displaystyle f\) as follows. For any acute-angled triangle \(\displaystyle XYZ\), if \(\displaystyle P\) is a point on \(\displaystyle YZ\), then \(\displaystyle f(P;XYZ)\) is defined as the line joining the feet of perpendiculars from \(\displaystyle P\) to lines \(\displaystyle XY\); \(\displaystyle XZ\).
Let \(\displaystyle ABC\) be a triangle with orthocenter \(\displaystyle H\). Let \(\displaystyle A'B'C'\) be the orthic triangle of \(\displaystyle ABC\). Let \(\displaystyle A''\equiv f(B';HCA) \cap f(C';HAB)\). Similarly, points \(\displaystyle B''\); \(\displaystyle C''\) are defined. Show that the lines \(\displaystyle AA''\); \(\displaystyle BB''\); \(\displaystyle CC''\) are concurrent.
Proposed by K. V. Sudharshan
(6 pont)
solution (in Hungarian), statistics
B. 5029. Assume that a certain football team have played 1000 games altogether, and scored 1000 points altogether since the team was founded. (A team score 3 points for every game they win, 1 point for a draw and no points for games they lose.) Prove that there are at most \(\displaystyle {(2.9)}^{1000}\) possible sequences of the 1000 scores.
(6 pont)
 |
Problems with sign 'A'Deadline expired on May 10, 2019. |
A. 749. Given are two polyominos, the first one is an L-shape consisting of three squares, the other one contains at least two squares. Prove that if \(\displaystyle n\) and \(\displaystyle m\) are co-prime then at most one of the \(\displaystyle n\times n\) and \(\displaystyle m\times m\) boards can be tiled by translated copies of the two polyominos.
Proposed by: András Imolay, Dávid Matolcsi, Ádám Schweitzer and Kristóf Szabó, Budapest
(7 pont)
solution (in Hungarian), statistics
A. 750. Let \(\displaystyle k_1,\ldots,k_5\) be five circles in the plane such that \(\displaystyle k_1\) and \(\displaystyle k_2\) are externally tangent to each other at point \(\displaystyle T\), \(\displaystyle k_3\) and \(\displaystyle k_4\) are externally tangent to both \(\displaystyle k_1\) and \(\displaystyle k_2\), \(\displaystyle k_5\) is externally tangent to \(\displaystyle k_3\) and \(\displaystyle k_4\) at points \(\displaystyle U\) and \(\displaystyle V\), respectively, moreover \(\displaystyle k_5\) intersects \(\displaystyle k_1\) at \(\displaystyle P\) and \(\displaystyle Q\), like shown in the figure.
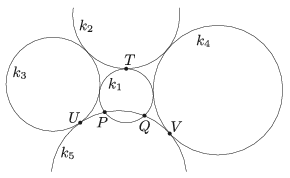
Show that
\(\displaystyle \frac{PU\cdot PV}{QU\cdot QV} = \frac{PT^2}{QT^2}. \)
(7 pont)
solution (in Hungarian), statistics
A. 751. Let \(\displaystyle c>0\) be a real number, and suppose that for every positive integer \(\displaystyle n\), at least one percent of the numbers \(\displaystyle 1^c,2^c,3^c,\ldots,n^c\) are integers. Prove that \(\displaystyle c\) is an integer.
(7 pont)
Upload your solutions above.
