KöMaL Problems in Mathematics, November 2022
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on December 12, 2022. |
K. 739. Phil made the following observations throughout a certain period in autumn:
1. During that period, there were 11 days when it rained.
2. A rainy morning was always followed by a sunny afternoon.
3. Altogether, there were 9 sunny mornings and 12 sunny afternoons.
How many days were there when it did not rain at all?
(5 pont)
solution (in Hungarian), statistics
K. 740. In how many different ways is it possible to tile a \(\displaystyle 3\times12\) rectangle with twelve \(\displaystyle 1\times3\) rectangles?
(5 pont)
solution (in Hungarian), statistics
K. 741. Starting with the numbers \(\displaystyle 1, 2, 3, 4, 5, 6, 7, 8, 9\), in each step two numbers are chosen and increased by 1. Is it possible to achieve that each number is 10?
(5 pont)
 |
Problems with sign 'K/C'Deadline expired on December 12, 2022. |
K/C. 742. Danny is learning the alphabet. He has successfully named the first eight letters (A, B, C, D, E, F, G, H), but the order of the letters was not entirely correct. Only five of the eight letters were listed in the right position (i.e. in the position where it occurs in the alphabet). How many such orders of the eight letters are there?
(5 pont)
solution (in Hungarian), statistics
K/C. 743. The midpoint of side \(\displaystyle BC\) of a rectangle \(\displaystyle ABCD\) is \(\displaystyle E\), and \(\displaystyle F\) is the point lying closer to \(\displaystyle D\) which divides side \(\displaystyle CD\) in a \(\displaystyle 2:1\) ratio. The midpoint of line segment \(\displaystyle AE\) is \(\displaystyle G\), and \(\displaystyle H\) is the point lying closer to \(\displaystyle E\) which divides line segment \(\displaystyle EF\) in a \(\displaystyle 2:1\) ratio. What fraction is the area of triangle \(\displaystyle FGH\) of the area of rectangle \(\displaystyle ABCD\)?
(5 pont)
 |
Problems with sign 'C'Deadline expired on December 12, 2022. |
C. 1738. A natural number is called balanced, if the number of digits in its representation in decimal notation equals the number of different prime factors it has. For example, \(\displaystyle 21\) is balanced, but \(\displaystyle 42\) is not. Is it true that there are infinitely many balanced numbers?
Proposed by K. A. Kozma, Győr
(5 pont)
solution (in Hungarian), statistics
C. 1739. Define the following functions on the largest possible subset of the set of real numbers: \(\displaystyle f(x)=\sqrt{x+5}\,\), \(\displaystyle g(x)=\frac{-2x+8}{5}\) and \(\displaystyle h(x)=[x+3]\) (here \(\displaystyle [a]\) denotes the integer part of the real number \(\displaystyle a\), that is, the greatest integer which is not greater than \(\displaystyle a\)). Find the common points of the graphs of the three functions.
Proposed by B. Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
C. 1740. \(\displaystyle P\) is an interior point of side \(\displaystyle CD\) of a parallelogram \(\displaystyle ABCD\), and \(\displaystyle Q\) is an interior point of side \(\displaystyle AB\) parallel to \(\displaystyle CD\). The intersection of line segments \(\displaystyle PA\) and \(\displaystyle QD\) is \(\displaystyle M\), and the intersection of line segments \(\displaystyle PB\) and \(\displaystyle QC\) is \(\displaystyle N\).
Assume that \(\displaystyle MN\nparallel{AB}\), and \(\displaystyle MN\) intersects the line of \(\displaystyle CD\) at point \(\displaystyle X\), and the line of \(\displaystyle AB\) at point \(\displaystyle Y\). Prove that \(\displaystyle DX=BY\).
(American competition problem)
(5 pont)
solution (in Hungarian), statistics
C. 1741. The diagonals \(\displaystyle AC\) and \(\displaystyle BD\) of a convex quadrilateral \(\displaystyle ABCD\) intersect at \(\displaystyle M\). Is it possible that the areas of triangles \(\displaystyle ABM\), \(\displaystyle BCM\), \(\displaystyle CDM\) and \(\displaystyle DAM\), in this order, are four consecutive terms of
\(\displaystyle a)\) an arithmetic sequence;
\(\displaystyle b)\) a geometric sequence?
Proposed by B. Bíró, Eger
(5 pont)
solution (in Hungarian), statistics
C. 1742. Consider the following functions (defined on the largest possible subset of the set of real numbers):
\(\displaystyle f_0(x)=\frac{1}{1-x}, \quad\text{and}\quad f_n(x)=f_0\big(f_{n-1}(x)\big), \)
for all positive integers \(\displaystyle n\). Calculate the value of \(\displaystyle f_{2022}(2022)\).
(Canadian problem)
(5 pont)
 |
Problems with sign 'B'Deadline expired on December 12, 2022. |
B. 5270. \(\displaystyle n^2\) regular triangles of unit side are used to make a large regular triangle of side \(\displaystyle n\) units. The small triangles are coloured alternately dark and light. The numbers \(\displaystyle 1, 2, 3,\dots, n^2\) are written in the triangles, as shown in the figure. What is the sum of the numbers in the dark triangles?
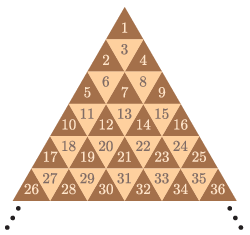
Proposed by L. Németh, Fonyód
(3 pont)
solution (in Hungarian), statistics
B. 5271. \(\displaystyle ABC\) is an isosceles right angled triangle with the right angle lying at vertex \(\displaystyle C\). \(\displaystyle A'\), \(\displaystyle B'\) and \(\displaystyle C'\) are interior points of sides \(\displaystyle AB\), \(\displaystyle BC\) and \(\displaystyle CA\), respectively, such that triangle \(\displaystyle A'B'C'\) is similar to \(\displaystyle ABC\).
Show that the midpoint of the side \(\displaystyle AB\), the midpoint of line segment \(\displaystyle A'B'\), and point \(\displaystyle C\) are collinear.
Proposed by E. Hajdu, Sopron and M. Hujter, Budapest
(3 pont)
solution (in Hungarian), statistics
B. 5272. A flea starts out from point \(\displaystyle (a,b)\) of the coordinate plane, where \(\displaystyle a\), \(\displaystyle b\) are positive integers. With each jump, the flea will move one unit to the left or downwards. It keeps jumping until it reaches either the \(\displaystyle x\) axis or the \(\displaystyle y\) axis. What fraction of the possible sequences of jumps terminate on the \(\displaystyle x\) axis?
Based on the idea of D. Melján, Kecskemét
(4 pont)
solution (in Hungarian), statistics
B. 5273. \(\displaystyle D\) is a point on side \(\displaystyle AB\) of an equilateral triangle \(\displaystyle ABC\), and \(\displaystyle E\) is a point on side \(\displaystyle BC\) such that \(\displaystyle \angle BCD =45^\circ\) and \(\displaystyle \angle CDE =30^\circ\). Show that \(\displaystyle BE=2AD\).
Proposed by S. Róka, Nyíregyháza
(4 pont)
solution (in Hungarian), statistics
B. 5274. The product of the positive integers \(\displaystyle a<b\) is a perfect square. Show that there is a positive integer \(\displaystyle x\) such that \(\displaystyle a\le x^2\le b\).
Proposed by S. Róka, Nyíregyháza
(5 pont)
solution (in Hungarian), statistics
B. 5275. Is there an irrational number \(\displaystyle a\) such that \(\displaystyle a^{\sqrt{3}}\) is rational?
Proposed by B. Hujter, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 5276. Prove that there exist infinitely many positive integers \(\displaystyle k\) for which the sum of the digits of \(\displaystyle 2^k\) is
\(\displaystyle a)\) smaller;
\(\displaystyle b)\) greater
than the sum of the digits of \(\displaystyle 2^{k+1}\).
Proposed by Cs. Sándor, Budapest
(6 pont)
solution (in Hungarian), statistics
B. 5277. The centre of the inscribed circle of triangle \(\displaystyle ABC\) is \(\displaystyle I\). The midpoint of the circular arc \(\displaystyle BCA\) is \(\displaystyle F\), and line \(\displaystyle FI\) intersects the circumscribed circle again at point \(\displaystyle M\). Show that line \(\displaystyle CM\) passes through the external centre of similitude of the inscribed circle and the circumscribed circle.
Proposed by G. Kós, Budapest
(6 pont)
 |
Problems with sign 'A'Deadline expired on December 12, 2022. |
A. 836. For every \(\displaystyle i \in \mathbb{N}\) let \(\displaystyle A_i\), \(\displaystyle B_i\) and \(\displaystyle C_i\) be three finite and pairwise disjoint subsets of \(\displaystyle \mathbb{N}\). Suppose that for every partition of \(\displaystyle \mathbb{N}\) consisting of sets \(\displaystyle A\), \(\displaystyle B\) and \(\displaystyle C\) there exists \(\displaystyle i\in \mathbb{N}\) such that \(\displaystyle A_i \subset A\), \(\displaystyle B_i \subset B\) and \(\displaystyle C_i \subset C\). Prove that there also exists a finite \(\displaystyle S\subset \mathbb{N}\) such that for every partition of \(\displaystyle \mathbb{N}\) consisting of sets \(\displaystyle A\), \(\displaystyle B\) and \(\displaystyle C\) there exists \(\displaystyle i\in S\) such that \(\displaystyle A_i \subset A\), \(\displaystyle B_i \subset B\) and \(\displaystyle C_i \subset C\).
Submitted by András Imolay, Budapest
(7 pont)
A. 837. Let all the edges of tetrahedron \(\displaystyle A_1A_2A_3A_4\) be tangent to sphere \(\displaystyle S\). Let \(\displaystyle a_i\) denote the length of the tangent from \(\displaystyle A_i\) to \(\displaystyle S\). Prove that
\(\displaystyle \bigg(\sum_{i=1}^4 \frac 1{a_i}\bigg)^{\!\!2}> 2\bigg(\sum_{i=1}^4 \frac1{a_i^2}\bigg). \)
Submitted by Viktor Vígh, Szeged
(7 pont)
A. 838. Sets \(\displaystyle X\subset \mathbb{Z}^{+}\) and \(\displaystyle Y\subset \mathbb{Z}^{+}\) are called comradely, if every positive integer \(\displaystyle n\) can be written as \(\displaystyle n=xy\) for some \(\displaystyle x\in X\) and \(\displaystyle y\in Y\). Let \(\displaystyle X(n)\) and \(\displaystyle Y(n)\) denote the number of elements of \(\displaystyle X\) and \(\displaystyle Y\), respectively, among the first \(\displaystyle n\) positive integers.
Let \(\displaystyle f\colon \mathbb{Z}^{+}\to \mathbb{R}^{+}\) be an arbitrary function that goes to infinity. Prove that one can find comradely sets \(\displaystyle X\) and \(\displaystyle Y\) such that \(\displaystyle \frac{X(n)}{n}\) and \(\displaystyle \frac{Y(n)}{n}\) goes to \(\displaystyle 0\), and for all \(\displaystyle \varepsilon>0\) exists \(\displaystyle n \in \mathbb{Z}^+\) such that
\(\displaystyle \frac{\min\big\{X(n), Y(n)\big\}}{f(n)}<\varepsilon. \)
(7 pont)
Upload your solutions above.
