|
|
|
|
|
|
| [278] Hajba Károly | 2006-03-03 12:55:11 |
 Üdv!
Egy kicsit pontosíts kérlek, mert nekem az upload-ra egy hófehér lap jött be (Firefox, MIE). Keresésnél pedig csak ezt a statikát találtam:
Keresés abc-sorrendbe rendezésidôrendbe rendezés
Építész- és építőmérnök >> Szilárdságtan és tartószerkezet
Rövid leírásKategóriaOldalszám
Statika Tételsor 3 oldal
...
Mely szintén üres (nálam).
|
| Előzmény: [275] hobbymatekos, 2006-03-03 11:18:05 |
|
|
| [276] Simon | 2006-03-03 11:55:10 |
 Isten vagy HOBBYMATEKOS!!!
|
|
|
| [274] Simon | 2006-03-03 08:40:31 |
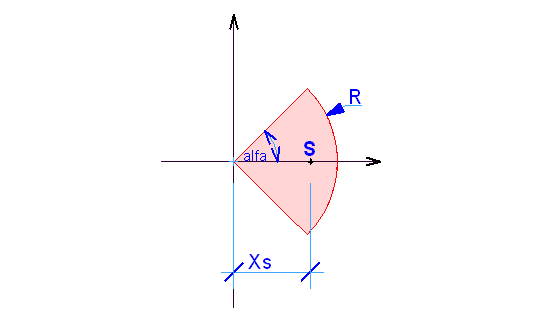
 Sziasztok! tudnátok segíteni? milyen képlet segítségével tudom kiszámítani a negyedkör súlypontját?
|
|
|
|
|
| [270] hobbymatekos | 2006-02-28 15:13:22 |
 Érdektelen eset. Gamma(x+1) ha x természetes szám, éppen x! (Egyébként 1. Hiszen 1/gamma(n) pólusai a negativ egészek és a nulla, 1x-esek és a rezidumok (-1)**n/n! Hankel int. formulával. 0!=1)
|
| Előzmény: [269] nadorp, 2006-02-26 17:18:00 |
|
|
| [268] Sirpi | 2006-02-26 11:02:38 |
 Ajánlom figyelmedbe a 230-as hsz-t. Ott a feladat ki van tűzve (helyesen :-) ), és az utána következő 1-2 hsz-ben a megoldást is megtalálod. Tudom, hogy ismétlés a tudás anyja, de akkor is :-)
|
| Előzmény: [264] hobbymatekos, 2006-02-23 21:18:56 |
|
|
|
|
|
| [263] nadorp | 2006-02-23 20:37:34 |
 Szia !
Gondoltam, hogy nem Joe megoldásához szóltál hozzá, ez "csak" egy egyszerű dícséret volt. Én is a végtelen leszállás módszerrel próbálkoztam, de Joe-é jóval egyszerűbb az enyémnél.
|
| Előzmény: [262] hobbymatekos, 2006-02-23 19:51:35 |
|
| [262] hobbymatekos | 2006-02-23 19:51:35 |
 Sziasztok 241 és 242 válasz: Ez csak egy ötlet volt. Most pontosan nincs ilyen alakú megoldás. Azaz: a-Sqr(k) sem és a+ Sqr(k) sem gyök. (Egyébként nem Joe megoldásához szóltam.)Most ha a=7, k=5 akkor b nem egész.
|
| Előzmény: [242] nadorp, 2006-02-06 11:56:35 |
|
|
| [260] rizsesz | 2006-02-23 15:45:15 |
 Apropó, nem tudjátok megmondani, hogy 1/(n-k)! k szerinti deriváltja micsoda? Általában létezik ilyen? :)
|
|




 (0)=?
(0)=?
