| [31] Lóczi Lajos | 2004-01-21 13:46:23 |
 Először is pár megjegyzés: a gamma-függvényt definiáló integrálalak csak x>0 (illetve Re x>0, ahol Re a valós rész) esetén helyes. Negatív x-ekre a definíció más.
Másodszor a feladat kitűzésében nem szerencsés, hogy x jelöli mind az integrációs változót, mind az integrálás felső határát.
A "folytonosított függvény" kifejezés helyett a "folytonos kiterjesztés" a bevett szóhasználat. A faktoriális és a gamma függvény közötti kapcsolatban pedig vigyázni kell az indexeltolásra (aminek történeti okai vannak): n!= (n+1), ha n pozitív egész. (n+1), ha n pozitív egész.
Ezek után tehát az a kérdés, milyen valós x-ekre áll fenn, hogy
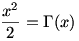
.
Pozitív x-ekre pontosan 2 megoldás van, az egyik kb. 1,33615, a másik kb. 4,34884. (Az, hogy van megoldás, folytonossági és határértéket tartalmazó meggondolásokból jön ki. A megoldások számához "kis" x-ekre konvexitási érvelés vezet, "nagy" x-ekre pedig az a tény, hogy a gamma-függvény viselkedése ilyen x-ekre ismert (Stirling-formula és társai), amiből látható, hogy a gamma-függvény sokkal "gyorsabban nő", mint bármely polinom, s így elég nagy x-ektől kezdve nincs megoldás.)
A gamma-függvénynek a nempozitív egészeknél pólusai vannak ("végtelenné válik"), az egyenletnek a negatív számok körében is vannak megoldásai, és a grafikonokat nézve számomra úgy tűnik, végtelen sok (melyek minden bizonnyal szintén nem adhatók meg rövidebb leírással, mint "a fenti egyenlet negatív megoldásai", numerikusan természetesen itt is bármelyiket akármilyen pontossággal ki lehet számolni, pl. egy negatív megoldás kb. -3,0347).
|
| Előzmény: [30] Gubbubu, 2004-01-20 19:26:37 |
|
| [30] Gubbubu | 2004-01-20 19:26:37 |
 Üdv mindenkinek!
Az "ujjgyakorlatok" c. témakörben szerepelt egy feladat: oldjuk meg a
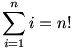
egyenletet!
Ennek a feladatnak a "folytonos analogonja" is kitűzhető (más kérdés, hogy akad-e valaki, aki megoldja:
13. fa. Oldjuk meg a
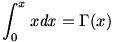
egyenletet (x R)! A gammafüggvény bizonyos értelemben a faktoriális "folytonosított függvénye": R)! A gammafüggvény bizonyos értelemben a faktoriális "folytonosított függvénye":
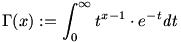
.
|
|
| [29] Gubbubu | 2004-01-16 21:59:49 |
 Kedves László:
A lényeget mindig elfelejtem! Igen, a  (n) a szám pozitív osztóinak összege, tehát (n) a szám pozitív osztóinak összege, tehát  (n)=1+d2+...+dd(n)-1+n, di az n osztói. (n)=1+d2+...+dd(n)-1+n, di az n osztói.
A "Számelméleti érdekességek" c. topikban definiáltam már ezt, itt még nem. Ezentúl nem csak itt, hanem minden számelméleti jellegű szövegben (ezt általában egyértelműen el lehet dönteni) ebben az értelemben fogom használni a  (n) jelet (minden hozzászólásomban azért mégse akarom mindig definiálni). Előfordulhat esetleg, hogy (n) jelet (minden hozzászólásomban azért mégse akarom mindig definiálni). Előfordulhat esetleg, hogy  valaminek a szórását jelöli, de ez a feladat szövegéből és képleteiből azért gondolom, kiderül majd. valaminek a szórását jelöli, de ez a feladat szövegéből és képleteiből azért gondolom, kiderül majd.
Üdv:G.
|
| Előzmény: [28] lorantfy, 2004-01-16 19:15:48 |
|
|
| [27] Gubbubu | 2004-01-16 18:55:52 |
 Üdv;
Egy határértékszámítási példa, remélem, jó nehéz lesz (ha nem, hát nem):
12. fa.: Jelölje Sn az n-edik háromszögszámot, más néven az első n természetes szám összegét. Igazoljuk, hogy
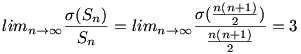
Megjegyzés: a határértéket részben empirikusan, részben a Derive programmal számoltam ki, így a feladat elvileg megoldható, és a benne foglalt állítás vsz. igaz.
|
|
| [26] Csizmadia Gábor | 2004-01-13 20:54:19 |
 A gyakorlatot vezető tanárodnak nagyon nem volt igaza, ugyanis a felső határ - akár elemi módszerekkel is - tetszőlegesen megközelíthető.
Gosztonyi Balázstól származik a következő megoldás.
Pozitív n,k,r számokra érvényes az alábbi mértani-számtani közép közti egyenlőtlenség:
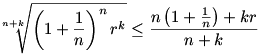
Válasszuk meg úgy k-t ér r-t, hogy a jobb oldal 1 legyen, ilyenkor:
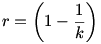
Visszaírva az eredeti kifejezésbe:
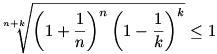
Ezután (n+k)-adik hatványra emelve, és kirendezve 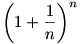 -re: -re:
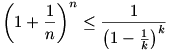
Pl. k=100 esetén
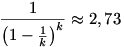
|
| Előzmény: [25] bbb, 2004-01-13 18:28:57 |
|
| [25] bbb | 2004-01-13 18:28:57 |
 Sziasztok!
Elsős egyetemista koromban analízis gyakorlaton azt bizonyítottuk, hogy az 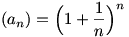 sorozat korlátos, pl. felső korlát a 3. A gyakorlatot vezető tanár úr szerint ennél pontosabb becslés nem is adható a felső korlátra elemi módszerekkel (tehát határértékszámítás használata nélkül). Felajánlotta, hogy ha ez valakinek mégis sikerülne, annak ad egy tábla csokoládét. Nekem sikerült, ám még mindig nem kaptam meg a megéremelt jutalmat. De mindez lényegtelen. A feladat a következő lenne: bbh sorozat korlátos, pl. felső korlát a 3. A gyakorlatot vezető tanár úr szerint ennél pontosabb becslés nem is adható a felső korlátra elemi módszerekkel (tehát határértékszámítás használata nélkül). Felajánlotta, hogy ha ez valakinek mégis sikerülne, annak ad egy tábla csokoládét. Nekem sikerült, ám még mindig nem kaptam meg a megéremelt jutalmat. De mindez lényegtelen. A feladat a következő lenne: bbh
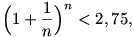
ahol n=1,2,.... A bizonyításhoz mellőzzétek a határértékszámításból tanultakat, mert így igazán izgalmas. Jó munkát!
|
|
| [24] Csizmadia Gábor | 2003-12-24 00:54:31 |
 Ugyan nem tudom, hogy ez kinek mennyire nehéz, de szerintem ezek a feladatok megérdemlik, hogy ide kerüljenek, leginkább a C. Az A és a B esetén nem csak konkrét példára gondolok, hanem egy kicsit általánosabb megoldásra.
10. feladat Konstruálj olyan valós-valós (R->R) függvényt (ha létezik ilyen), amely értelmezési tartományának minden nem megszámlálható részhalmazán felveszi a teljes értékkészletet. A. Az értékkészlet ekvivalens N-nel B. Az értékkészlet ekvivalens N-nel, valamint a függvény mindenütt differenciálható C. Az értékkészlet ekvivalens R-rel
|
|
|
|
| [21] Rácz Béla | 2003-12-16 21:52:54 |
 Egy igazi ínyencség, amit egyes érdekes ízlésű emberek diákolimpiára (1,5 óra/feladat) akartak kitűzni:
9. feladat
Mely (f, g) valósokon értelmezett valósértékű függvénypárokra teljesül minden x és y esetén az alábbi egyenlőség?
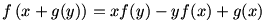
|
|
| [20] Pach Péter Pál | 2003-12-12 19:44:27 |
 Egy újabb feladat:
8. feladat
Legyen  >0. Keressük a legnagyobb >0. Keressük a legnagyobb  számot, amelyre teljesül, hogy ha n elég nagy, akkor megadható ( számot, amelyre teljesül, hogy ha n elég nagy, akkor megadható ( - - )n különböző egész szám 1 és n között úgy, hogy a megadott számok közül egyik sem osztója egy másik kétszeresének. Adjuk meg 1 és n között a lehető legtöbb egész számot ezzel a tulajdonsággal. )n különböző egész szám 1 és n között úgy, hogy a megadott számok közül egyik sem osztója egy másik kétszeresének. Adjuk meg 1 és n között a lehető legtöbb egész számot ezzel a tulajdonsággal.
Megjegyzés:
Félreértések elkerülése végett:  -t nem -t nem  függvényében keressük. függvényében keressük.
|
|
|
| [18] nadorp | 2003-12-12 16:17:28 |
 Kedves Béla !
Most lehet,hogy égni fogok, de közlök egy megoldást a 6. feladatra. Nem tudom elhinni, hogy csak a triviális megoldás létezik ( azaz a sorozat elemei egyenlőek ), de a hibát nem találom. Szóval:
Legyen a p polinom n-ed fokú és írjunk fel egy Euklideszi algoritmushoz hasonlót
p(x)=(x-q2)p1(x)+q1
p1(x)=(x-q3)p2(x)+r2
p2(x)=(x-q4)p3(x)+r3
. . .
pn-2(x)=(x-qn)pn-1(x)+rn-1
Ebből következik, hogy a p polinom alkalmas s2,s3,...sn+1 racionális számokkal felírható a következő alakba:
p(x)=(x-q2)...(x-qn+1)sn+1+(x-q2)...(x-qn)sn+...(x-q2)s2+q1
A fenti eljáráshoz hasonlóan,"eggyel később kezdve",alkalmas t2,t3,...tn+1 számokkal
p(x)=(x-q3)...(x-qn+2)tn+1+(x-q3)...(x-qn+1)tn+...(x-q3)t2+q2
Írjunk a második egyenlőségben x helyére p(x)-et és használjuk fel egyrészt a qi számok közti összefüggést, másrészt, hogy minden polinomban p(x)-p(a)=(x-a)h(x) minden "a" számra. Kapjuk:
p(p(x))=(x-q2)...(x-qn+1)hn+1(x)+(x-q2)...(x-qn)hn(x)+...(x-q2)h2(x)+q1, ahol hi(x) alkalmas racionális együtthatós polinom. Az előzőek alapján
p(p(x))+p(x)=(x-q2)...(x-qn+1)(hn+1(x)+sn+1)+(x-q2)...(x-qn)(hn(x)+sn)+...(x-q2)(h2(x)+s2)+q1+q2
Ha most a fenti egynlőségben x=q3, akkor azt kapjuk, hogy
(q3-q2)(h2(x)+s2)=0
Mivel h2(x) legalább elsőfokú polinom, ez csak úgy lehet, hogy q2=q3.
Teljesen hasonló módszerrel kapjuk, hogy q3=q4 stb. Végül a q3=q2 összefüggésből p(q3)=p(q2), azaz q2=q1 következik.
|
| Előzmény: [16] Rácz Béla, 2003-12-11 00:30:39 |
|
| [17] Rácz Béla | 2003-12-11 19:42:01 |
 Eszembe jutott még egy darab. Nagyon örülnék neki, ha valaki elegáns megoldást adna rá, mert én csak elég kellemetlen bizonyításról tudok. A feladat egy háromszögben a beírt kör középpontjának az Euler-egyeneshez való viszonyát tisztázza:
7. feladat
A beírt kör K középpontjából a súlypontot és a magasságpontot összeköző SM szakasz több, mint 90°-ban látszik; más szóval K benne van az SM átmérőjű körben.
Sőt, ez az állítás éles: ha adottak az S,M,K pontok úgy, hogy ez a feltétel teljesüljön, akkor rajzolható hozzájuk megfelelő háromszög.
|
|
| [16] Rácz Béla | 2003-12-11 00:30:39 |
 Ez a magyar-izraeli versenyen volt pár éve:
6. feladat
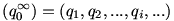 egy végtelen sorozat, ami racionális számokból áll; és p egy legalább másodfokú racionális együtthatós polinom. Tudjuk, hogy p(qi+1)=qi minden lehetséges i-re. egy végtelen sorozat, ami racionális számokból áll; és p egy legalább másodfokú racionális együtthatós polinom. Tudjuk, hogy p(qi+1)=qi minden lehetséges i-re.
Bizonyítandó, hogy a (q) sorozat periodikus.
|
|
| [15] Pach Péter Pál | 2003-12-08 20:40:47 |
 Kedves Péter!
A G gráf egy automorfizmusa: csúcsainak egy  permutációja, amelyre az i és j pontok közötti élek száma megegyezik a permutációja, amelyre az i és j pontok közötti élek száma megegyezik a  (i) és (i) és  (j) pontok közötti élek számával minden (i,j) párra. (j) pontok közötti élek számával minden (i,j) párra.
Részletezve: Megszámozzuk a gráf pontjait 1-től n-ig(, ha n pontja van). Tegyük fel, hogy ezután át tudjuk számozni a gráf pontjait úgy, hogy minden 1 i i j j n esetén teljesül, hogy ha az i. és j. pont között a „régi” számozás mellett futott él, akkor az „új” számozás mellett is fut és ha a „régi” számozás mellett nem futott él, akkor az „új” mellett sem fut. (Amennyiben a gráf nem egyszerű, akkor azt is megköveteljük, hogy ugyanannyi él fusson.) Az „új” számozást (vagyis a gráf pontjainak ezt a permutációját) a gráf egy automorfizmusának nevezzük. Minden gráfnak van legalább egy automorfizmusa: az identitás (amikor minden pont száma változatlan marad). (Általában egy „véletlenszerűen” felrajzolt gráfnak nincs is más automorfizmusa.) n esetén teljesül, hogy ha az i. és j. pont között a „régi” számozás mellett futott él, akkor az „új” számozás mellett is fut és ha a „régi” számozás mellett nem futott él, akkor az „új” mellett sem fut. (Amennyiben a gráf nem egyszerű, akkor azt is megköveteljük, hogy ugyanannyi él fusson.) Az „új” számozást (vagyis a gráf pontjainak ezt a permutációját) a gráf egy automorfizmusának nevezzük. Minden gráfnak van legalább egy automorfizmusa: az identitás (amikor minden pont száma változatlan marad). (Általában egy „véletlenszerűen” felrajzolt gráfnak nincs is más automorfizmusa.)
Példák:
- Az n pontú teljes gráfnak automorfizmusainak száma n!.
- Egy (2<)n hosszú kör automorfizmusainak száma 2n.
- A Petersen-gráf automorfizmusainak száma 120.
Az automorfizmusokat pedig úgy szorozhatjuk össze, hogy összeszorozzuk a hozzájuk tartozó permutációkat. Innen már végig lehet gondolni, hogy valóban csoportot alkotnak…
A példádat egyébként ismerem, úgyhogy Attilára, vagy másra vár a feladat, hogy megoldja, és feltegye a megoldást.
|
| Előzmény: [11] nadorp, 2003-12-08 13:53:55 |
|
| [14] Pach Péter Pál | 2003-12-08 20:29:51 |
 Térjünk vissza a 3. feladathoz, és a [4]-ben feltettem kérdésemhez. A kérdésre a válasz az, hogy nem, és nem csak „ehhez hasonlóan” nem bizonyítható, hanem egyáltalán nem, ugyanis nem is igaz.
A feladat átfogalmazható úgy, hogy 0<y1,y2,…,yn esetén igaz-e, hogy 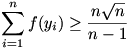 , ha , ha 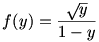 . .
Az f függvény a ![\left[0;\sqrt{\frac43}-1\right]](keplet.cgi?k=D8FAC312033F382D) intervallumon konkáv, a intervallumon konkáv, a 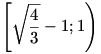 intervallumon pedig konvex. Ezt f’’(x) előjelének vizsgálatával (amihez másodfokú egyenletet kell megoldanunk) állapíthatjuk meg. intervallumon pedig konvex. Ezt f’’(x) előjelének vizsgálatával (amihez másodfokú egyenletet kell megoldanunk) állapíthatjuk meg.
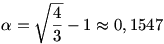
Ha n=3, akkor ha y1,y2,y3 mind legalább  , akkor készen vagyunk a Jensen-egyenlőtlenséggel. Ha közülük egy, vagy kettő , akkor készen vagyunk a Jensen-egyenlőtlenséggel. Ha közülük egy, vagy kettő  -nál kisebb, akkor a többi „annyira nagy” lesz, hogy még erősebb becslést nyerünk. (Ezt viszonylag gyorsan ki lehet hozni.) Viszont, ha n nagy, akkor lehetséges, hogy akár az összes yi kisebb, mint -nál kisebb, akkor a többi „annyira nagy” lesz, hogy még erősebb becslést nyerünk. (Ezt viszonylag gyorsan ki lehet hozni.) Viszont, ha n nagy, akkor lehetséges, hogy akár az összes yi kisebb, mint  , s ilyenkor éppen a Jensen-egyenlőtlenség mutatja, hogy , s ilyenkor éppen a Jensen-egyenlőtlenség mutatja, hogy 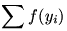 még csökkenthető. (Hiszen a [0; még csökkenthető. (Hiszen a [0; ] intervallumon f konkáv.) ] intervallumon f konkáv.)
|
| Előzmény: [4] Pach Péter Pál, 2003-12-02 23:05:43 |
|
|
|
| [11] nadorp | 2003-12-08 13:53:55 |
 Kedves Attila !
Teljesen igazad van abban, hogy a rendezettségen alapuló egyenlőtlenség nagyon hasznos. Ha érdekel, nézd meg a KÖMAL A.324. sz. példára adott harmadik megoldást, nagyon tanulságosan használja fel ezt az egyenlőtlenséget.
Kedves Péter ! (különben én is az vagyok)
Az első példa kapcsán - valószínűleg anno kihagytam pár absztrakt algebrai előadást - kisebb gondjaim vannak azzal, hogy hogyan értelmezzem egy gráf automorfizmusát ( kétféle leképezést is találtam egy konkrét esetben, így az egyik biztos nem jó). Légy szíves pár szóval vázold. Van egy aranyos példám is. Az 198[3-8] évben tűzték ki a Riesz Frigyes matek versenyen.
4.feladat
Adott egy n-elemű X halmaz ( n 1 pozitív egész ) és adott X-nek n darab különböző ( nem feltétlenül valódi ) részhalmaza A1,A2...An. BBh. létezik x 1 pozitív egész ) és adott X-nek n darab különböző ( nem feltétlenül valódi ) részhalmaza A1,A2...An. BBh. létezik x X , hogy az A1\{x},A2\{x} … An\{x} halmazok is különbözőek. X , hogy az A1\{x},A2\{x} … An\{x} halmazok is különbözőek.
|
|
| [10] jenei.attila | 2003-12-08 10:43:51 |
 Kedves nadorp!
Teljesen igazad van, amikor leírtam, már én is rájöttem. Ahogy említettem is, nem gondoltam végig, csak egy ötlet volt, először jónak tűnt.
A harmadik feladatnál nem kell használni a "skalár szorzatos" (nem tudok rá jobb nevet, és ennyi erővel a Cauchy-Schwartz egyenlőtlenséget is lehetne így nevezni) egyenlőtlenséget, mert a feladathoz elég a
(x-y)2+(x-z)2+(y-z)2 0 0
egyenlőtlenséget átrendezni, azonban a "skalár szorzatos" önmagában is érdekes és sokszor nagyon hasznos egyenlőtlenség.
|
|
|
| [8] nadorp | 2003-12-08 09:30:10 |
 Kedves Attila !
A 3. feladatra adott ötleted annyiban hibás,hogy a 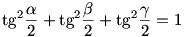 feltételből csak annyi következik, hogy feltételből csak annyi következik, hogy  + + + + <=180o (Jensen egyenlőtlenség), tehát nem biztos, hogy egyáltalán háromszöget kapsz.Pld. próbáld ki a <=180o (Jensen egyenlőtlenség), tehát nem biztos, hogy egyáltalán háromszöget kapsz.Pld. próbáld ki a 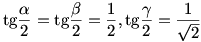 esetet, esetet,  + + + + =176,78o-ot fogsz kapni. =176,78o-ot fogsz kapni.
Egyébként,ha  , , , , egy háromszög szögei, akkor könnyű a bizonyítás, mert a tan egy háromszög szögei, akkor könnyű a bizonyítás, mert a tan  +tan +tan  +tan +tan  =tan =tan  tan tan  tan tan  azonosság miatt, felhasználva a számtani és mértani közép közötti összefüggést: azonosság miatt, felhasználva a számtani és mértani közép közötti összefüggést:
(tan  +tan +tan  +tan +tan  )3>=27tan )3>=27tan  tan tan  tan tan  =27(tan =27(tan  +tan +tan  +tan +tan  ), ezért ), ezért
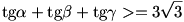
|
| Előzmény: [7] jenei.attila, 2003-12-07 23:00:44 |
|
| [7] jenei.attila | 2003-12-07 23:00:44 |
 Kedves Péter!
A negyedik feladat megoldásával is megelőzött nadorp, azért leírom az enyémet:
A megoldás során két jól ismert egyenlőtlenséget fogunk felhasználni. Az egyik a hatványközepekre vonatkozó egyenlőtlenség, amely szerint ha    , akkor nem negatív számok , akkor nem negatív számok  -adik hatványközepe nem nagyobb a -adik hatványközepe nem nagyobb a  -adik hatványközepüknél. x,y,z négyzetes és köbös hatványközepére: -adik hatványközepüknél. x,y,z négyzetes és köbös hatványközepére:
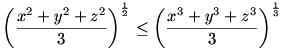
Mindkét oldalt 6-odik hatványra emelve, és 8/9 -del beszorozva kapjuk:
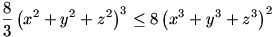
A másik egyenlőtlenség két számsorozat "skaláris szorzatára" vonatkozik, amely szerint az akkor maximális, ha a sorozatok egyezőleg rendezettek, minimális, ha ellenkezőleg rendezettek. Például x,y,z -re
xy+yz+zx x2+y2+z2 x2+y2+z2
A bizonyítandó egyenlőtlenség bal oldalának zárójeles kifejezéseire alkalmazva a számtani-mértani közép egyenlőtlenségét majd köbre emelve és 9-cel beszorozva:
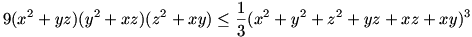
Ebben az egyenlőtlenségben a jobboldal (a "skalár szorzatos" egyenlőtlenség miatt):
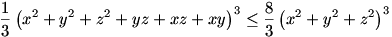
A két utóbbi és a hatványközepekre vonatkozó egyenlőtlenséget összevetve kapjuk a bizonyítandó állítást:
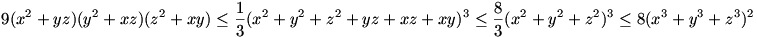
A 3. feladat megoldását nem gondoltam végig, mert nadorp megoldása egyszerűbb, azért ezt is leírom. Az 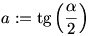 helyettesítést bevezetve a bizonyítandó egyenlőtlenség helyettesítést bevezetve a bizonyítandó egyenlőtlenség 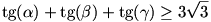 . A feltételek . A feltételek  , , , , hegyesszögű háromszöget adnak meg. hegyesszögű háromszöget adnak meg.
|
| Előzmény: [2] Pach Péter Pál, 2003-12-01 22:09:03 |
|



 (n+1), ha n pozitív egész.
(n+1), ha n pozitív egész. 
 R)! A gammafüggvény bizonyos értelemben a faktoriális "folytonosított függvénye":
R)! A gammafüggvény bizonyos értelemben a faktoriális "folytonosított függvénye":  (n) a szám pozitív osztóinak összege, tehát
(n) a szám pozitív osztóinak összege, tehát 



 >0. Keressük a legnagyobb
>0. Keressük a legnagyobb  számot, amelyre teljesül, hogy ha n elég nagy, akkor megadható (
számot, amelyre teljesül, hogy ha n elég nagy, akkor megadható ( permutációja, amelyre az i és j pontok közötti élek száma megegyezik a
permutációja, amelyre az i és j pontok közötti élek száma megegyezik a  i
i ,
, egy háromszög szögei. Ebből a rendezési tétel (amit „skalár szorzatos egyenlőtlenség”-nek hívtál) alapján látszik, hogy 1
egy háromszög szögei. Ebből a rendezési tétel (amit „skalár szorzatos egyenlőtlenség”-nek hívtál) alapján látszik, hogy 1 1 pozitív egész ) és adott X-nek n darab különböző ( nem feltétlenül valódi ) részhalmaza A1,A2...An. BBh. létezik x
1 pozitív egész ) és adott X-nek n darab különböző ( nem feltétlenül valódi ) részhalmaza A1,A2...An. BBh. létezik x