| [6] Pach Péter Pál | 2003-12-04 22:32:09 |
 Kedves Péter! (Csak tippeltem, ha tévedek, javíts ki!)
Köszi a megoldást a 4. feladatra. A 3. feladatnál szerintem azért nem zavaró a 2-es szorzó elhagyása, mert az egyenlet 0-ra volt rendezve. A [4]-ben feltett kérdésemen nagyon sokat nem érdemes töprengeni, ugyanis kicsit becsapós. :-) Nos?
Sok sikert az első két feladathoz!
|
| Előzmény: [5] nadorp, 2003-12-04 14:12:26 |
|
| [5] nadorp | 2003-12-04 14:12:26 |
 Kedves Péter !
A 3. feladatra adott megoldás nem annyira remek, mert egyrészt elhagytam a nevezőben egy 2-es szorzót ( bár ez a lényegen nem változtat), másrészt nem általánosítható n>3 esetére, mert ekkor 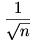 csak egyszeres gyök, ezért nem a négyzeten szerepel a szorzatban. Azért még küzdök vele.Viszont van egy megoldásom a 4. feladatra. csak egyszeres gyök, ezért nem a négyzeten szerepel a szorzatban. Azért még küzdök vele.Viszont van egy megoldásom a 4. feladatra.
Elég bizonyítani, hogy
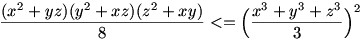
Vonjunk mindkét oldalból 6-ik gyököt. Ekkor
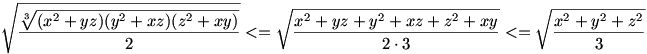
Felhasználva hogy a 2-dik hatványközép kisebb egyenlő a 3-dik hatványközépnél, a bizonyítandó állítást kapjuk
|
| Előzmény: [2] Pach Péter Pál, 2003-12-01 22:09:03 |
|
|
| [3] nadorp | 2003-12-02 17:11:35 |
 Megoldás a 3. feladatra.
Az ember a szimmetria miatt akaratlanul arra gondol, egyenlőség csak 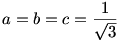 esetén van. Ekkor a balodalon álló összes tört értéke esetén van. Ekkor a balodalon álló összes tört értéke 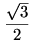 . Másrészt . Másrészt 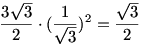 is teljesül, ezért az is teljesül, ezért az
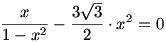
egyenletnek az 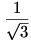 szám gyöke,ezért belőle a szám gyöke,ezért belőle a 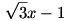 kifejezés kiemelhető. Valóban, nem részletezve a számolást, a fenti egyenlet bal oldalára a következőt kapjuk: kifejezés kiemelhető. Valóban, nem részletezve a számolást, a fenti egyenlet bal oldalára a következőt kapjuk:
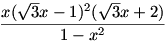 , ami a (0;1) nyílt intervallumon nemnegatív. , ami a (0;1) nyílt intervallumon nemnegatív.
Most már az eredeti feladat könnyen megoldható. A fenti egyenelet bal oldalán szereplő kifejezésbe helyettesítsük rendre az a,b és c számokat és adjuk össze ezt a három kifejezést. Felhasználva a négyzetösszegekre vonatkozó feltételt, pont a kívánt egyenlőtlenséget kapjuk.
|
| Előzmény: [2] Pach Péter Pál, 2003-12-01 22:09:03 |
|
| [2] Pach Péter Pál | 2003-12-01 22:09:03 |
 A továbbiakban „Bizonyítsuk be, hogy” röviden „Bbh” lesz. Kezdetnek négy feladat: (Kedvcsinálónak könnyebb példa is van köztük. :-))
1. feladat: Bbh bármely véges csoporthoz létezik olyan véges egyszerű gráf, amelynek az automorfizmuscsoportja izomorf vele.
2. feladat: Bbh egy gráfban akkor és csak akkor létezik teljes párosítás, ha akárhogyan is hagyunk el néhány pontot (és a belőlük kiinduló éleket), a maradékban a páratlan komponensek száma nem nagyobb az elhagyott pontok számánál. Megjegyzés: bocs mindenkitől, aki ismeri.
3. feladat: 0<a,b,c<1 és a2+b2+c2=1. Bbh
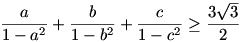
4. feladat: x,y,z nemnegatívak, bbh
9(x2+yz)(y2+zx)(z2+xy) 8(x3+y3+z3)2 8(x3+y3+z3)2
|
|
| [1] Pach Péter Pál | 2003-12-01 22:04:53 |
 Azért nyitottam ezt a témát, hogy a nehezebb példákat is kitűzhessük valahol. Tehát itt olyan feladatokat adnánk fel és oldanánk meg, amiket nem írunk be az Érdekes matekfeladatok-hoz, mert nehéznek érezzük őket. Természetesen kevésbé nehéz példákat is kitűzhetünk, senki se tartson vissza példát csupán azért, mert aggódik, hogy az nem elég kemény.
|
|




 8(x3+y3+z3)2
8(x3+y3+z3)2