| [737] HoA | 2013-11-18 15:26:19 |
 A követelmény úgy is megfogalmazható, hogy minden kiválasztott négyzetnek páros, minden nem kiválasztott négyzetnek páratlan számú kiválasztott szomszédja legyen.
|
| Előzmény: [734] kurthyg, 2013-11-17 00:44:52 |
|
| [736] kurthyg | 2013-11-17 11:04:40 |
 A kiválasztandó négyzetek sorozata. Számozzuk be a négyzeteket: a bal fölső sarok az 1-es a jobb alsó nxn: tehát balról jobbra és föntről lefelé növekszenek a számok.
Ekkor az út (ha eredetileg minden négyzet fehér volt): 1 3 5 7 9
Ezeket sorban kiválasztva minden négyzet fekete lesz.
|
| Előzmény: [735] Sinobi, 2013-11-17 10:48:31 |
|
|
| [734] kurthyg | 2013-11-17 00:44:52 |
 A következő feladatot szeretném megosztani (persze, lehet, hogy már volt, kb 15 éve olvastam KöMaL-t utoljára, még gimnáziumban).
Adott egy nxn-es négyzetrács csupa fehér négyzettel. Válasszuk ki valamelyik négyzetet, ekkor a kiválasztott négyzet, a tőle jobbra és balra, alatta és fölötte lévők feketévé változnak. És minden egyes későbbi kiválasztás ellentétes színűre változtatja a kiválasztott négyzetet és a szomszédait.
Feladat olyan utat találni, amelynek végén az összes négyzet fekete lesz. Hogyan adható meg általános megoldás?
(Pl.: 1x1-es nél triviális. 2x2-esnél minden négyzetet ki kell választani. 3x3-asnál a sarkokat és a középső négyzetet.)
A probléma általánosítása: az nxn-es négyzetrács néhány négyzete fehér, néhány négyzete fekete. Milyen út vezet csupa fekete négyzethez? Hogyan kereshető meg a megoldás? Van-e mindig megoldás?
|
|
| [733] w | 2013-10-25 23:07:23 |
 A következő egy rendkívül érdekes, a pozitív valós számokra bizonyítandó egyenlőtlenség (négyzetreemelve a valósokra is érvényes marad!). Annál inkább érdekes, hogy milyen egyszerű alakú, negyedfokú egyenlőtlenség.
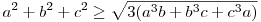
Különösen szokatlan az egyenlőség-esete, amit mindenképpen érdemes előre megfigyelni.
(A feladat egyébként valamennyire ismert, egy idő múlva majd elárulom, hol találtam.)
|
|
|
| [731] Sinobi | 2013-10-20 01:36:18 |
 Bocsánat, nem ilyen alakra kell a végén hozni. Ezt még tovább kell alakítanod, hogy l:=-14/9*m, s akkor azt kapod, hogy:
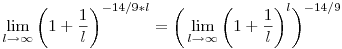
Amiben még mindig ott van n a kitevőben. De azzal nem tudsz semmit se kezdeni. Igazából már Euler se tudott vele semmit kezdeni, csak feltűnt neki, hogy az olyan kifejezéseknek, melyekben n a kitevőben van, a limesze gyakran 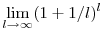 -lel és algebrai műveletekkel megadható, ezért a -lel és algebrai műveletekkel megadható, ezért a 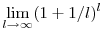 -et elnevezte magáról e-nek. Azóta általában az a feladat, hogy a kapott sorozatokat valahogy leredukáljuk erre a kifejezésre. -et elnevezte magáról e-nek. Azóta általában az a feladat, hogy a kapott sorozatokat valahogy leredukáljuk erre a kifejezésre.
|
| Előzmény: [730] Sinobi, 2013-10-20 01:12:11 |
|
| [730] Sinobi | 2013-10-20 01:12:11 |
 Mit tanultatok már határértékből? Szerintem valami ilyesmi kell legyen:
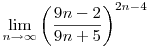
kicsit alakítjuk a limesz mögött álló formulát:
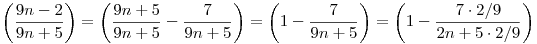
bevezetjük az 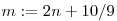 változót. Ekkor a képletünk: változót. Ekkor a képletünk:
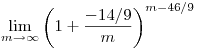
amit szétbontva két limesz szorzatára (majd megnézzük, hogy léteznek):
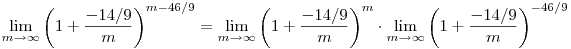
A szorzat jobb oldala 1-hez tart, a bal oldala e^-14/9-hez, tehát az eredeti is e^-14/9-hez, ami tényleg kb 0.2110.
|
| Előzmény: [729] wartburg, 2013-10-19 23:16:25 |
|
| [729] wartburg | 2013-10-19 23:16:25 |
 Kedves Topictársak, sehogy sem boldogulok az alábbi határérték feladattal: keressük az alábbi sorozat határértékét: [(9*n-2)/(9*n+5)]#(2*n-4) (a # jel hatvány jelet takarna, tehát a (2*n-4) a tört kitevője) Nem bírom a hatványt "levarázsolni" a kifejezésből, s a tört számlálóját és nevezőjét is leosztva n-nel én egyet kapnék határértéknek, ami viszont bármilyen kitevővel egy lenne. Ugyanakkor persze az Excel függvény ábrázolás szerint 0,22XXXX lenne valahol a határérték, de nekem nem jön ki ez "tudományosan". Előre is köszönöm a segítséget!
|
|
|
|
| [726] nadorp | 2013-10-09 12:42:30 |
 Ettől persze az állítás nem igaz. Legyen f(x) a következő
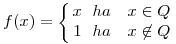
Ekkor f(x) a racionális számok között additív, viszont tetszőleges r irracionális számra
f(r+1)=1 2=f(r)+f(1) 2=f(r)+f(1)
|
| Előzmény: [725] nadorp, 2013-10-09 09:26:56 |
|
|
| [724] Ménkűnagy Bundáskutya | 2013-10-09 08:45:17 |
 2. (valós) Legyen A azon valós számok halmaza, melyeknek tizedestört alakja
*,*11...110s0a10a20a30a4...,
vagyis valahonnan kezdve minden második jegy 0, előtte pedig néhány (esetleg 0 darab) 1-es áll (ez üres feltétel, csak így világosabb lesz). A függvény legyen A-n kívül 0, egy A-beli elemre pedig vegyük az első olyan pontot, ahonnan ez fennáll: x=*,*0s0a10a2..., és s előtt három jeggyel nem 0 áll. A 0s előtt közvetlenül álló egyesek száma legyen N. Ekkor legyen f(x)=(-1)s.N,a1a2a3....
Legyen [a,b] tetszőleges nemelfajuló intervallum, y pedig tetszőleges valós szám. Kezdjünk felírni egy valós számot. Az első sok jegyét állítsuk be úgy, hogy azok garantálják, hogy [a,b]-be esik. Ezután tegyünk le száz darab 2-est, majd |y| egész része darab 1-est, ezután lőjük be az előjelet, majd írjuk be y tizedesjegyeit 0-kal összefésülve. Az így kapott szám f-értéke y.
(komplex) Legyen f egy jó valós-valós függvény. Legyen hozzá F:C C a következő: F(x+iy)=f(x)+if(y). Tetszőleges kicsi négyzetben, körben stb van tengelypárhuzamos téglalap, és ha F(x+iy)=u+iv a cél, akkor legyen x a téglalap valós vetületéből olyan, hogy f(x)=u, y pedig a képzetes vetületből olyan, hogy f(y)=v. Ekkor F(x+iy)=f(x)+if(y)=u+iv. C a következő: F(x+iy)=f(x)+if(y). Tetszőleges kicsi négyzetben, körben stb van tengelypárhuzamos téglalap, és ha F(x+iy)=u+iv a cél, akkor legyen x a téglalap valós vetületéből olyan, hogy f(x)=u, y pedig a képzetes vetületből olyan, hogy f(y)=v. Ekkor F(x+iy)=f(x)+if(y)=u+iv.
|
| Előzmény: [722] marcius8, 2013-10-08 12:41:31 |
|
|
| [722] marcius8 | 2013-10-08 12:41:31 |
 Ha valaki tud, segítsen:
1. Egy f(x) függvény additív, ha minden "p" és "q" számra teljesül, hogy f(p+q)=f(p)+f(q). Igaz-e hogy ha egy függvény a racionális számok halmazán additív, akkor ez a függvény a valós számok halmazán is additív?
2. Keressünk olyan R-->R függvényt, amely minden intervallumon minden valós számot felvesz. Illetve keressünk olyan C-->C függvényt, amely minden "négyzet alakú tartományon" (vagy "minden kör alakú tartományon") minden komplex számot felvesz.
Mindenkinek köszönöm a segítségét. Bertalan Zoltán.
|
|
|
|
| [719] izsák | 2013-10-07 09:46:14 |
 Érdekes, hogy két "amatőr" beszélget szimpla matek problémáról, a matematikusok hallgatnak, vagy (ha az eddig válaszolók azok,) akkor hamis válaszokat adnak. Senki nem tudja a választ?
|
| Előzmény: [718] Zilberbach, 2013-10-03 13:32:27 |
|
| [718] Zilberbach | 2013-10-03 13:32:27 |
 Igen, a maximuma x=1 -nél van, akkor a kitöltési tényező = 100
X=1 -től x=1,999... -ig monoton csökken.
x=2 -nél a kitöltési tényező értéke hirtelen fölugrik, majd ismét monoton csökken egészen 3 -ig, ahol megint hirtelen megnő, majd ismét monoton csökken 4 -ig.
A függvény azután is ugrál: egy ideig monoton csökken, azután hirtelen megugrik, majd megint monoton csökken, de már nem csak egész számonként, hanem egyre gyakrabban.
|
| Előzmény: [717] izsák, 2013-10-03 08:32:28 |
|
| [717] izsák | 2013-10-03 08:32:28 |
 Igaz! Ott minimuma van a függvénynek. A maximuma milyen x értéknél lehet? X=1 ? A kettő között és x>2 esetén hogyan alakulhat? Milyen lehet a függvény alakja?
|
| Előzmény: [716] Zilberbach, 2013-10-02 20:24:42 |
|
|
| [715] Zilberbach | 2013-10-02 11:32:06 |
 Ehhez kapcsolódva lenne nekem is egy kérdésem.
Ha a kitöltendő nagy gömb sugara = r, és a kitöltéshez használt kisebb gömbök sugara = r/x, akkor milyen x értéknél kapjuk a legalacsonyabb kitöltési tényezőt?
|
| Előzmény: [705] izsák, 2013-09-25 08:05:38 |
|
| [714] Erben Péter | 2013-10-01 11:55:11 |
 Itt van egy elég alapos történeti áttekintés: http://bib.irb.hr/datoteka/402976.main1.pdf
Ha jól értem, az 1828-as Möbius cikk olyan - elég magas fokszámú - polinomot ad meg, amely kapcsolatot termet az oldalak hossza, a köréírt kör sugara, és a sokszög területe között. (Általában n-oldalú húrsokszögekkel foglalkozott.)
A Robbins-cikket még nem találtam meg, így azt nem tudtam megnézni, hogy adott-e explicit formulát n=5 esetén.
|
| Előzmény: [713] marcius8, 2013-10-01 10:49:59 |
|
| [713] marcius8 | 2013-10-01 10:49:59 |
 Köszönöm, hogy foglalkoztál az általam felvetett kérdéssel. Az az igazság, hogy akármit is csináltam, mindig az lett a vége, hogy egy ötödfokú egyenletet kell megoldani. Valószínűleg az általad felírt egyenlet is ötödfokúra vezethető vissza. Tisztelettel: Bertalan Zoltán
|
| Előzmény: [712] w, 2013-09-30 20:11:49 |
|







 2=f(r)+f(1)
2=f(r)+f(1)
 C a következő: F(x+iy)=f(x)+if(y). Tetszőleges kicsi négyzetben, körben stb van tengelypárhuzamos téglalap, és ha F(x+iy)=u+iv a cél, akkor legyen x a téglalap valós vetületéből olyan, hogy f(x)=u, y pedig a képzetes vetületből olyan, hogy f(y)=v. Ekkor F(x+iy)=f(x)+if(y)=u+iv.
C a következő: F(x+iy)=f(x)+if(y). Tetszőleges kicsi négyzetben, körben stb van tengelypárhuzamos téglalap, és ha F(x+iy)=u+iv a cél, akkor legyen x a téglalap valós vetületéből olyan, hogy f(x)=u, y pedig a képzetes vetületből olyan, hogy f(y)=v. Ekkor F(x+iy)=f(x)+if(y)=u+iv.
