|
| [162] joe | 2005-07-03 20:37:46 |
 Jól sejted, kitől kaptam, de nem 9-es vagyok, csak régebben hallottam, és talán rossz topicba tettem. Leht, h nem nehéz, de szép! Vagy nem?
|
| Előzmény: [160] Doom, 2005-07-02 15:41:59 |
|
|
| [160] Doom | 2005-07-02 15:41:59 |
 Lehet, hogy ez neked triviális, de ha jól sejtem, kitől kapta ezt a "házi feladatot" :), akkor kb 9-es lehet az illető. És akkor már nem ilyen egyértelmű.... sztem. :)
Joe, kommentáld!:)
|
| Előzmény: [159] jonas, 2005-07-02 10:07:10 |
|
| [159] jonas | 2005-07-02 10:07:10 |
 Ez vagy triviális, vagy félreértettem.
Egyszerűen veszed az eni pontot minden egész n-re. Akkor ennek minden n/2 hajlásszögű egyenes (az origón át) szimmetriatengelye, de mégsincs szimmetriaközéppontja.
Azért nyilvánvaló, hogy ilyesmit keresünk, mert ha két szimmetriatengely metszi egymást, akkor az alakzat már forgásszimmetrikus a tengelyek szögének kétszeresével, tehát ha ez a szög  racionális többszöröse, akkor már középpontosan szimmetrikus is. racionális többszöröse, akkor már középpontosan szimmetrikus is.
|
| Előzmény: [157] joe, 2005-07-01 19:09:37 |
|
|
| [157] joe | 2005-07-01 19:09:37 |
 130. feladat: Döntsük el, létezik-e olyan, síkbeli ponthalmaz, melynek végtelen sok szimmetriatengelye van, legalább két ilyen tengely metszi egymást, de a ponthalmaznak nincs egyetlen egy szimmetriaközéppontja sem.
|
|
|
|
|
|
|
|
| [150] Lóczi Lajos | 2005-05-18 21:16:11 |
 129. feladat. Van-e olyan 0<a, 0<b, a b számpár, melyre ab=b(ab/a)? b számpár, melyre ab=b(ab/a)?
|
|
| [149] Lóczi Lajos | 2005-05-18 00:32:07 |
 128. feladat. Legyen p>0 szám. Határozzuk meg a
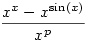
kifejezés határértékét, ha x 0 (x>0). 0 (x>0).
|
|
| [148] Lóczi Lajos | 2005-05-05 23:33:04 |
 127. feladat. Ismeretes, hogy tetszőleges, rögzített pozitív egész M esetén a
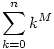
összeg felírható "zárt alakban", például
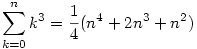
ahol n tetszőleges természetes szám.
Adjuk meg a zárt alak általános képletét M függvényében!
|
|
|
| [146] Lóczi Lajos | 2005-04-25 10:45:03 |
 Aki szeret egyenlőtlenségekkel játszadozni, annak íme egy feladat. Az egyenlőtlenség természetes módon merült fel egy bizonyítás részeként, tehát nem tenyészproblémáról van szó :-)
125. feladat: Mutassuk meg, hogy fennáll az alábbi egyenlőtlenség, ha n tetszőleges természetes szám, h és alfa pedig olyan pozitív valós számok, hogy szorzatuk kisebb, mint pl. 2/25:
|
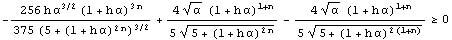 |
|
| [145] levi | 2005-04-22 15:51:02 |
 Be kell húzni az AE vagy CD pontokon átmenő egyenes(ek)et. Ekkor ott vagyunk, hogy már megint háromszögeket kapunk, és akkor már megint vagy az van hogy a végtelenségig kapjuk a háromszögeket vagy ismét behúzunk egy olyan egyenest amit te rajzoltál, de ezzel már megint új pontokat kapunk, amiket össze kell kötnünk a többivel, ismét csak háromszögeket kapva...
|
| Előzmény: [143] nadorp, 2005-04-22 09:07:32 |
|
|
| [143] nadorp | 2005-04-22 09:07:32 |
 Kedves Levi !
Nem mindig keletkezik DEF háromszög.
Más:
Visszatérve a hengeres példára, van egy kicsit egyszerűbb megoldás is ( ez persze semmit nem von le a Joe által közölt eljárás érdeméből):
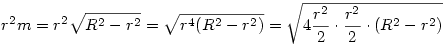 , és innen már mehet a számtani és mértani közép közti összefüggés a gyök alatti kifejezésre. , és innen már mehet a számtani és mértani közép közti összefüggés a gyök alatti kifejezésre.
|
 |
| Előzmény: [142] levi, 2005-04-21 22:41:20 |
|
| [142] levi | 2005-04-21 22:41:20 |
 Bizonyítsuk be, hogy nem lehet az (euklideszi) síkban véges számú pontot megadni úgy, hogy ha minden egyes pontpár által meghatározott egyenest behúzunk, akkor minden egyes ilyen egyenesre legalább három pont illeszkedik a megadottak közül!
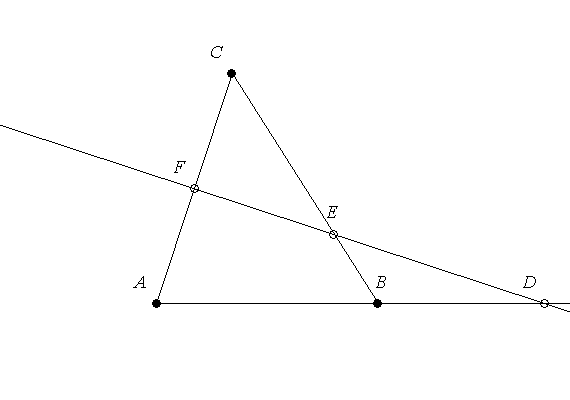
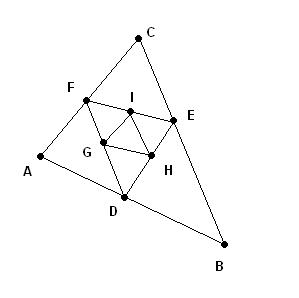
Próbáljunk meg keresni egy ilyen N (véges) számot. Először jelöljünk ki a sikban 3 nem egy egyenesre eső pontot. Ezek akkor meghatároznak egy háromszöget. Legyen ez ABC háromszög. Azt szeretnénk, ha minden oldalon lenne még egy pont (hogy meglegyen az egyenesenkénti 3 pont). Jelöljük ezeket D,E,F-fel. Ekkor azonban a DEF háromszögben áll fenn az előző eset. Jelöljük G,H,I pontokat a megfelelő oldalakon. Ez újabb háromszöget határoz meg, tehát ezt a végtelenségig lehet folytatni, azaz nem lehet véges számú pontot megadni. Ha az ABC háromszőgnél a D vagy E ill. F pontokat nem a háromszög oldalán jelöljük ki, hanem azon az egyenesen, ami átmegy az A és B pontokon, azzal sem "nyerünk" semmit, hiszen azzal csak egy újabb háromszöget jelöltünk ki, amiben ismét csak nem lehet véges számú pontot megadni.
|
 |
| Előzmény: [124] joe, 2005-04-06 19:17:25 |
|
| [141] joe | 2005-04-21 20:07:26 |
 Szerintem jó, legalábbis az eredmény; a többi megítélésére így hirtelen nem vállalkoznék, mert hajlamos vagyok a "bizonyítási hézagokat" átugrálni.
Szerintem annyit egyszerűsíthetünk, hogy "ha a három egyenes közül semmelyik kettő nem esne egybe, akkor találnánk olyan pontot, ahol az egyik fgv.-érték negatív, a másik kettő pozitív". A többi egy kicsit bonyolult, de valószínűleg helyes. Egyébként ilyen "szorzatos függvényspekulációval" még nem találkoztam; nagyon jó ötlet, és egész biztosan máshol is használható.
Amire én gondoltam, az egy kicsit egyszerűbb, de csak miután az ember rájött. Valószínűleg azt is egy helyenként homályos és egészében véve tekervényes gondolatmenet előzné meg. A módszer a következő:
Szorzatot tudunk összeggel fölülről becsülni (AG). Az (R-m)(R+m)m esetében két problémánk van:
1) Az egyenlőtlenség nem éles, mert a három tényező sosem lehet egyenlő,
2) A felső becslés is tartalmaz változót.
Mindkét probléma kiküszöbölhető az alábbi trükkel: a kifejezést beszorozzuk egy számmal; ez a szélsőérték helyén nyilván nem változtat. Úgy tekintjük, hogy mindhárom tényezőt egy bizonyos számmal szoroztuk, tehát keressük a(R-m)*b(R+m)*cm kif. maximumát. Az a, b, c -t úgy választjuk, hogy:
1) a(R-m) + b(R+m) + cm -ből kiessen az m (változó);
2) Az a(R-m) = b(R+m) = cm egyenletrendszernek egyértelmű megoldása legyen m-re.
Egyenlőre ennyire vállalkozom; a szétírást rábíznám olyasvalakire, aki jobban szeret (és tud) texelni, mint én...
|
| Előzmény: [140] levi, 2005-04-21 17:05:40 |
|
| [140] levi | 2005-04-21 17:05:40 |
 Tehát keressük az (R-m)(R+m)m szorzat maximumát(0<m<R, R>0). Ha felbontjuk a zárójeleket a -m3+R2m -et kapjuk. Általánosságban tehát keressük a f(x)=-x3+R2x függvény maximumhelyét (helyeit). Legyen x maximumhely, ekkor f(x) maximumérték, f(y) tetszőleges érték, ekkor teljesül az f(x)-f(y) 0. Ez egyenlő ezzel: -x3+R2x+y3-R2y 0. Ez egyenlő ezzel: -x3+R2x+y3-R2y 0. Kiemelések után: (y-x)(y2+xy+x2-R2) 0. Kiemelések után: (y-x)(y2+xy+x2-R2) 0. A második tag y-ra nézve egy másodfokú egyenletként is felfogható, tehát a felírható így: (y-y1)(y-y2), ahol y1 = 0. A második tag y-ra nézve egy másodfokú egyenletként is felfogható, tehát a felírható így: (y-y1)(y-y2), ahol y1 = 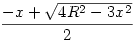 , y2= , y2=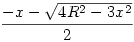 . Tehát az egyenletünket felírhatjuk 3 szorzatként: (y-x)(y-y1)(y-y2) . Tehát az egyenletünket felírhatjuk 3 szorzatként: (y-x)(y-y1)(y-y2) 0. Ezek az elsőfokú polinomok a koordinátasíkban az g(x)=x egyenessel párhuzamosak. Két eset lehetséges: vagy egybeesnek vagy nem. Ha nem esnek egybe, akkor lesz olyan hely ahol az egyik vagy mindhárom ellenkező előjelű lesz, ekkor f(x)-f(y) 0. Ezek az elsőfokú polinomok a koordinátasíkban az g(x)=x egyenessel párhuzamosak. Két eset lehetséges: vagy egybeesnek vagy nem. Ha nem esnek egybe, akkor lesz olyan hely ahol az egyik vagy mindhárom ellenkező előjelű lesz, ekkor f(x)-f(y) 0 vagy kettő lesz ellenkező előjelű ill. megegyezik az előjelük, és ekkor f(x)-f(y) 0 vagy kettő lesz ellenkező előjelű ill. megegyezik az előjelük, és ekkor f(x)-f(y) 0, tehát f(x) nem maximumérték, ezért x nem maximumhely. Tehát a 3 egyenesnek egybe kell esnie. Vizsgáljuk meg hogy mikor esik 2 egybe! 3 tag van, így 3 esetet kell megvizsgálni: x=y1, x=y2 vagy y1=y2. Az utóbbi esetben a másodfokú egyenlet diszkriminánsa nulla, azaz 4R2-3x2=0. Ebből x=2 0, tehát f(x) nem maximumérték, ezért x nem maximumhely. Tehát a 3 egyenesnek egybe kell esnie. Vizsgáljuk meg hogy mikor esik 2 egybe! 3 tag van, így 3 esetet kell megvizsgálni: x=y1, x=y2 vagy y1=y2. Az utóbbi esetben a másodfokú egyenlet diszkriminánsa nulla, azaz 4R2-3x2=0. Ebből x=2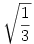 R, de ez nagyobb, mint R, tehát nem eleme az értelmezési tartománynak. Az x=y2 esetben nem valós szám a megoldás, míg x=y1 esetben: x= R, de ez nagyobb, mint R, tehát nem eleme az értelmezési tartománynak. Az x=y2 esetben nem valós szám a megoldás, míg x=y1 esetben: x=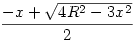 , rendezve 3x2=R2, amiből következik az x= , rendezve 3x2=R2, amiből következik az x=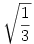 R. Ekkor y2=-2 R. Ekkor y2=-2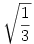 R, azaz y-y2=y+2 R, azaz y-y2=y+2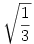 R. Ez mindig pozitív lesz (mert R>0, 0<y<R). Az első két tag is mindig pozitív lesz, azaz a szorzat mindig nagyobb-egyenlő lesz mint 0. A szorzat maximumát tehát az x= R. Ez mindig pozitív lesz (mert R>0, 0<y<R). Az első két tag is mindig pozitív lesz, azaz a szorzat mindig nagyobb-egyenlő lesz mint 0. A szorzat maximumát tehát az x=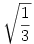 R helyen veszi fel. Visszatérve tehát a hengerhez, a m= R helyen veszi fel. Visszatérve tehát a hengerhez, a m=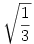 R, a sugár ( R, a sugár (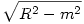 ) r= ) r=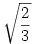 R, és a térfogat pedig V= R, és a térfogat pedig V=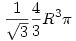 . (úgy érzem, hogy még finomítanom kellene ezen, egy helyen eléggé "bukdácsol" a bizonyítás...) . (úgy érzem, hogy még finomítanom kellene ezen, egy helyen eléggé "bukdácsol" a bizonyítás...)
|
|
| [139] Sirpi | 2005-04-21 14:28:40 |
 Végül én sem oldottam meg, valaki elmondta órán a megoldást. Továbbra is állítom, hogy szép feladat, és szerintem nehéz. Aki nem ismeri a trükköt, nem könnyen jön rá. Annyit szerintem még nyugodtan elárulhatunk, hogy a Fermat n=4-re való megoldhatatlanságánál a végtelen leszállás módszerére utaltál.
|
| Előzmény: [137] joe, 2005-04-20 20:35:34 |
|





 racionális többszöröse, akkor már középpontosan szimmetrikus is.
racionális többszöröse, akkor már középpontosan szimmetrikus is. 
 3 esetén -
3 esetén -

 b számpár, melyre ab=b(ab/a)?
b számpár, melyre ab=b(ab/a)? 0 (x>0).
0 (x>0). 2/3x2 függvény grafikonját, valamint forgassuk szintén az origó körül balra, de csak 45 fokkal az x
2/3x2 függvény grafikonját, valamint forgassuk szintén az origó körül balra, de csak 45 fokkal az x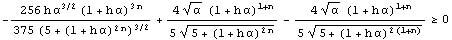



 0 vagy kettő lesz ellenkező előjelű ill. megegyezik az előjelük, és ekkor f(x)-f(y)
0 vagy kettő lesz ellenkező előjelű ill. megegyezik az előjelük, és ekkor f(x)-f(y)