|
| [371] Hajba Károly | 2006-09-28 10:54:08 |
 Először az erdő széle ferdén volt nálam, azért nem jöttem rögtön rá a javításra. Az új rajz szerint felírtam egy képletet, deriváltam is, de nem jött ki használható eredmény. Vagy elfelejtettem deriválni vagy rossz képletet állítottam fel. Jelenleg nem találom a hibámat, ezért helyben topogok. Legfeljebb grafikai úton tudnék iteratív módszerrel tovább lépni, de az időrabló tevékenység.
|
| Előzmény: [370] Sirpi, 2006-09-28 10:30:41 |
|
|
|
|
|
| [366] Sirpi | 2006-09-27 22:21:22 |
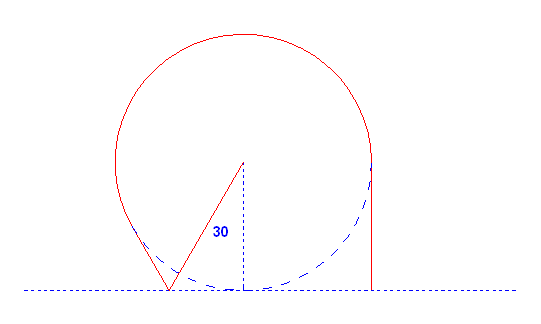
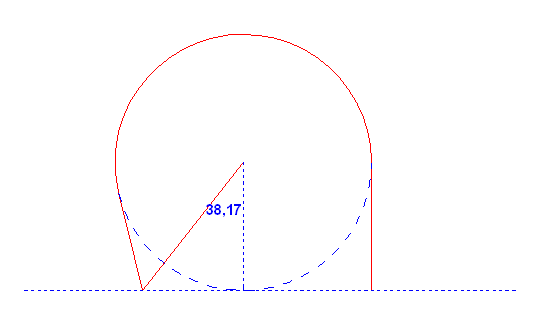
 Mivel a 6km sugaró kör kerületére mindenképp ki kell valamikor menni, vegyük az első pontot, ahol a kör határát érintjük. Eddig a pontig érdemes egyenes vonalban kivágtatni, különben nem optimális a stratégia. Asszem ezzel megcáfoltam a spirálelméletet :-)
|
| Előzmény: [365] Hajba Károly, 2006-09-27 19:40:29 |
|
| [365] Hajba Károly | 2006-09-27 19:40:29 |
 Elvileg nem egy olyan spirál eleje lenne, aminek a visszakanyarodó vonalszakaszai egyforma távolságra helyezkednek el?
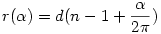
n N+ - spirálkör sorszáma N+ - spirálkör sorszáma
d - két spirálkör távolsága
|
| Előzmény: [364] Sirpi, 2006-09-27 16:11:17 |
|
| [364] Sirpi | 2006-09-27 16:11:17 |
 Egyébként ez az utolsó eredményem már 4 egymáshoz csatlakozó ívből jön ki, nem 3-ból, mint amiről az ábra készült. Ha lesz rá igény, írok róla bővebben, de éppen más is megteheti :-)
|
| Előzmény: [363] Sirpi, 2006-09-27 08:05:15 |
|
| [363] Sirpi | 2006-09-27 08:05:15 |
 38384m :-) És ezt már nem tudom tovább javítani, nem tudom, lehet-e.
Amúgy én nyáron a pusztafalui matektáborban másfél órás előadást tartottam erről a legrövidebb úthálózatos problémáról, úgyhogy talán nem szólnék hozzá egyelőre.
|
| Előzmény: [361] Sirpi, 2006-09-27 07:44:12 |
|
| [362] Hajba Károly | 2006-09-27 07:45:20 |
 Üdv!
Nehezítsük rizsesz előbbi példáját az aálatlánosítás felé:
- Mi a helyzet a szabályos ötszög esetén?
- Mely szabályos sokszögeknél lesz a legrövidebb úthálózat a sokszög kerülete és melyeknél nem?
|
|
|
|
| [359] Sirpi | 2006-09-26 12:17:09 |
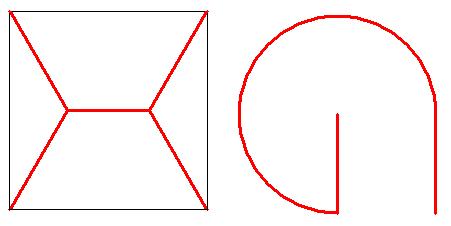
 Az első feladatnál annak belátásához, hogy az itt látható úthálózat optimális, érdemes felhasználni azt az önmagában is érdekes tényt, hogy minden olyan háromszögben, melynek legnagyobb szöge legfeljebb 120 fokos, a háromszög izogonális pontja az a pont, melynek a csúcsoktól vett távolságösszege minimális. Izogonális pontnak azt a pontot nevezzük, melyből minden oldal 120 fokos szög alatt látszik.
|
 |
| Előzmény: [358] rizsesz, 2006-09-26 11:06:20 |
|
| [358] rizsesz | 2006-09-26 11:06:20 |
 Kedves Sirpi és Yegreg!
Milyen vonalon mozognak a kedves feladatban szereplő barátaink?
|
|
|
| [356] rizsesz | 2006-09-25 23:02:38 |
 akkor elmondom, hogy én eddig mit gondolkodtam :) a kiindulási pontban állva, egy olyan vonalat kell rajzolni, ami amelynek akármilyen elforgatása mellett van közös pontja a szabadsággal. akármennyire akarom, nem tudom megtalálni a legjobb alakzatot. asszem még nem találkoztam ilyen feladattal nagyon.
|
|
|
| [354] rizsesz | 2006-09-25 22:07:25 |
 Igazából én buta vagyok :) a stratégia leglebutítottabb verziója, ha ember számára érthető, nekem már tökéletes. :)
|
|
|
|
| [351] rizsesz | 2006-09-25 18:06:09 |
 2 remek stratégia-alkotó feladat:
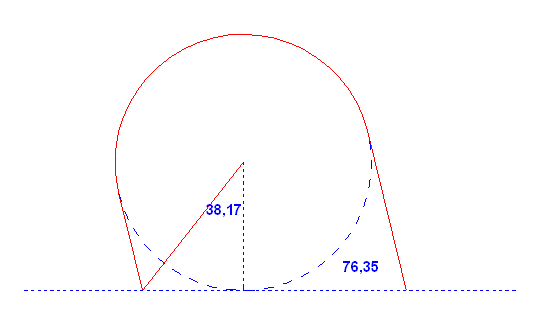
a., adott 4 város, melyek egy 20 egység oldalú négyzet sarkaiban vannak. lehetőségünk van 55 km út kiépítésére, de többre nem. ezek segítségével kiépíthető olyan út-rendszer, melyeken bármely városból bárhova el lehet-e jutni? b., Egy kirándulónk egy félsík alakú erdőben tévedt el. Ismert, hogy legfeljebb 6km-t tett meg az. A maratoni távnál kisebb séta alatt ki tud-e jutni, magyarul a legrosszabb esetben is olyan stratégiája van, hogy kijut.
|
|
| [350] jonas | 2006-09-18 13:45:23 |
 Nem is tudom.
Először is  amiből 2x=1/((1/x)/2) amiből pedig x2=exp(2log x) tehát a négyzetreemelést pontosan el tudjuk végezni. amiből 2x=1/((1/x)/2) amiből pedig x2=exp(2log x) tehát a négyzetreemelést pontosan el tudjuk végezni.
Ha lenne 2 alapú logaritmusunk és exponensünk is, akkor most egyszerű dolgunk lenne:
n=log2(2.2...2.2.1)
1=2n/2/2/.../2/2
|
| Előzmény: [349] rizsesz, 2006-09-18 13:00:49 |
|
| [349] rizsesz | 2006-09-18 13:00:49 |
 a [342]-es hozzászólásomra nincsen valakinek valami remek ötlete?
|
|
|




 N+ - spirálkör sorszáma
N+ - spirálkör sorszáma 



