| [567] Sirpi | 2007-12-06 11:40:44 |
 Nem tudom, volt-e már, de nekem egy feladat kapcsán a következő sorozat jött ki: a0=0, a1=1, majd a további indexekre:
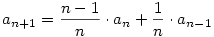
Ugye minden érték az előző kettő súlyozott számtani közepe, így a sorozat szűkülő intervallumokban oszcillál.
A feladat annak bizonyítása lenne, hogy ezeknek az [an,an+1] intervallumoknak 0-hoz tart a hossza, így a sorozatnak van határértéke, valamint mondjuk is meg, hogy mennyi.
Ha sikerült megoldanunk (nekem már igen :-) ), akkor elmondom majd azt is, hogy mi volt a feladat :-)
|
|
| [566] Cckek | 2007-07-31 11:01:18 |
 Észrevesszük, hogy x=0,y=z=1 illetve x=y=z=2 megoldások, és bebizonyítjuk, hogy nincs más megoldás. Ehez csak azt használjuk fel, hogy a jobboldal 5 többszöröse illetve Sophie Germaine híres képletét az-az a4+4b4=(a2-2ab+2b2)(a2+2ab+2b2). 3 hatványainak az utolsó számjegye 3,9,7,1 ha a hatványkitevő 4k+1,4k+2,4k+3,4k alakú, 4 hatványainak az utolsó számjegye 4,6 ha a hatványkitevő 2p+1,2p alakú. Tehát a baloldal csak akkor 5 többszöröse ha x=4k,y=2p+1 illetve x=4k+2,y=2p. Természetesen k,p>0
I. x=4k,y=2p+1 3x+4y=(3k)4+4(2p)4=(32k-3k2p+1+22p+1)(32k+3k2p+1+22p+1) s mivel jobboldalt 5 hatványa van ezért mindkét tényező osztható kell legyen 5-el de ekkor az különbségük is osztható 5-el, az az 3k2p+2 osztható 5-el ami lehetetlen. 3x+4y=(3k)4+4(2p)4=(32k-3k2p+1+22p+1)(32k+3k2p+1+22p+1) s mivel jobboldalt 5 hatványa van ezért mindkét tényező osztható kell legyen 5-el de ekkor az különbségük is osztható 5-el, az az 3k2p+2 osztható 5-el ami lehetetlen.
II. x=4k+2,y=2p 3x+4y=9.(3k)4+(2p)4=5.(3k)4+(2p)4+4.(3k)4 tehát (2p)4+4.(3k)4=(22p-2p+13k+32k)(22p+2p+13k+32k) osztható kell legyen 5-el az az mindkét tényező oszthato 5-el tehát különbségük 2p+23k osztható 5-el ami lehetetlen. 3x+4y=9.(3k)4+(2p)4=5.(3k)4+(2p)4+4.(3k)4 tehát (2p)4+4.(3k)4=(22p-2p+13k+32k)(22p+2p+13k+32k) osztható kell legyen 5-el az az mindkét tényező oszthato 5-el tehát különbségük 2p+23k osztható 5-el ami lehetetlen.
|
| Előzmény: [562] kdano, 2007-07-12 18:39:21 |
|
| [565] Lajos Arpad | 2007-07-21 10:45:42 |
 Ez nem olyan nehéz, de rá kell érezni a megoldásra. Melyik játék bonyolultabb, a sakk vagy a go? Miért?
|
|
| [564] Fálesz Mihály | 2007-07-13 10:59:19 |
 A feladatnak sok általánosítása létezik, íme egy, ami nem annyira közismert. (A KöMaL-ban is szerepelt már.)
Tekintsük az összes olyan 3n hosszúságú szót (betűsorozatot), ami n darab A-, n darab B- és n darab C-betűből áll. Ezeknek hányadrészére igaz, hogy tetszőleges 1 h h 3n-re az első h betű között legalább annyi A-betű van, mint B-betű, és legalább annyi B-betű, mint C-betű? 3n-re az első h betű között legalább annyi A-betű van, mint B-betű, és legalább annyi B-betű, mint C-betű?
A választ is elárulhatom, nem igazán segít a megoldásban: 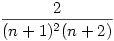 . .
A megoldás nehéz, de több pontján is nagyon bájos.
|
|
|
| [562] kdano | 2007-07-12 18:39:21 |
 Hát igen, én adottnak vettem a végeredményt. Amúgy szigorú vezetés mellett (ha a 0-0 állást megengedjük :P) nekem 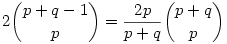 jött ki rossz esetre, azaz ugyanaz, mint neked :P Ezzel a valószínűség jött ki rossz esetre, azaz ugyanaz, mint neked :P Ezzel a valószínűség 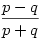 . .
Akkor itt egy következő feladat:
Keressük meg a 3x+4y=5z egyenlet összes pozitív egész számokból álló megoldását! (IMO Shortlist, 1991)
|
| Előzmény: [561] nadorp, 2007-07-12 08:36:58 |
|
| [561] nadorp | 2007-07-12 08:36:58 |
 Nálam a "vezetés" azt jelentette, hogy egyenlő állás nem megengedett, de ez most részletkérdés. Az összes eset az érdekesebb: én úgy értelmeztem a feladatot, hogy adott egy szavazás és a végeredménye n szavazat. Ekkor az n darab szavazat bármi lehet, mert a feladat szerint a szavazatok minden sorrendje azonos valószínűségű. Tehát én arra válaszoltam, hogy mennyi a valószínűsége annak, hogy P végig vezetett és p darab szavazatot kapott. Te pedig arra válaszoltál, hogy mennyi a valószínűsége annak, hogy P végig vezetett, feltéve, hogy végül p darab szavazatot kapott.
Amúgy valószínű, hogy a Te értelmezésed a jó.
|
| Előzmény: [560] kdano, 2007-07-11 20:31:33 |
|
|
|
| [558] Gyöngyő | 2007-07-06 18:07:03 |
 Sziasztok!
Itt egy feladat: Szavazási probléma.Tegyük fel,hogy egy választáson két jelölt van,P és Q. A P jelölt p szavazatot kapott,Q pedig q szavazatot,p>q.Ha a szavazatok minden sorrendje egyformán valószínű,akkor mi a valószínűsége annak,hogy a szavazatszámlálás során végig vezetett?
Üdv: Gyöngyő
|
|
| [557] jonas | 2007-07-04 09:50:17 |
 Na igen, ha a mértéket kihagyjuk, és csak a megszámlálhatót hagyjuk meg, akkor már valóban nem túl erős, hiszen az a legegyszerűbb (ha nem is az első) bizonyítás arra, hogy léteznek transzcendens számok.
|
| Előzmény: [556] Lóczi Lajos, 2007-07-03 20:03:47 |
|
| [556] Lóczi Lajos | 2007-07-03 20:03:47 |
 Szerintem meg ez a nagyágyú :), mert felhasználod, hogy e transzcendens (illetve, hogy van transzcendens szám). Az én érvelésemben a mérték szót sem kellett volna használni, pusztán a megszámlálható halmazok alaptulajdonságait.
|
| Előzmény: [550] jonas, 2007-07-03 12:46:34 |
|
| [555] Lóczi Lajos | 2007-07-03 20:00:17 |
 Sőt, az is igaz, hogy ha egy polinom minden együtthatója algebrai szám, akkor a gyökei is algebraiak. Ennek speciális eseteként rögtön adódik a válasz a kérdésre.
|
| Előzmény: [548] Cckek, 2007-07-02 14:42:48 |
|
|
| [553] Enkidu | 2007-07-03 17:11:25 |
 Sziasztok!
Ha a gyöke egy k-adfokú p(x) racionális együtthatós polinomnak, akkor p(x) = (x - a)(x - a2)...(x - ak). Ekkor a következő kn-edfokú q(x) szintén racionális együtthatós polinomnak 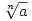 (persze az összes koplex gyök is) a gyöke: q(x) = (xn - a)(xn - a2)...(xn - ak) Innentől Jonas bizonyítja a hátralévő (persze az összes koplex gyök is) a gyöke: q(x) = (xn - a)(xn - a2)...(xn - ak) Innentől Jonas bizonyítja a hátralévő 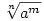 részt:). részt:).
Bocs az esetleges rossz képletekért még át kell néznem a TeX-et. Sziasztok
|
| Előzmény: [548] Cckek, 2007-07-02 14:42:48 |
|
|
| [551] jonas | 2007-07-03 12:48:49 |
 Igen, az algebrai számok résztestet alkotnak a valós vagy komplex számokban, de ezt nem elemi módon lehet könnyen bizonyítani, hanem algebrával. Ha kell a bizonyítása, akkor a régi algebra 1 vagy 2 füzeteimben utánanézhetek.
|
| Előzmény: [548] Cckek, 2007-07-02 14:42:48 |
|
| [550] jonas | 2007-07-03 12:46:34 |
 Szerintem ez nagyágyú ehhez. Egyszerűen mondhatjuk azt, hogy létezik transzcendens szám (mondjuk az e) és nyilván bármely x transzcendens számra és a racionális számra x+a is transzcendens, így pedig bármely intervallumba bele lehet tolni az e-t.
|
| Előzmény: [549] Lóczi Lajos, 2007-07-02 15:55:25 |
|
|
|
| [547] Cckek | 2007-07-02 14:03:48 |
 Minden nyílt intervallum tartalmaz transzcendens számokat. Kiváncsi vagyok az ötleteitekre.
|
|
|
| [545] xviktor | 2007-06-13 11:28:33 |
 Hali!
Paros fuggvenyeknel grafikus abrazolasban az y tengelyre szimmetrikus. (x tengelyre csak a konstans 0 az, egyebkent nem lenne fuggveny) :-)
Udv: Viktor
|
| Előzmény: [544] mrmorotz, 2007-06-13 11:22:29 |
|
| [544] mrmorotz | 2007-06-13 11:22:29 |
 A páros függvény olyan függvény, amelyre f(-x) = f(x) , minden x eleme Df-re. GRafikusan azok a páros függvények, amelyek képe szimmetrikus az x tengelyre. Például az x*x fv. ilyen. Páratlan: f(-x)=-f(x). Az ilyen fv. grafikonja szimmetrikus az origóra. Lásd köb(x).
|
| Előzmény: [536] amynna, 2007-06-08 17:35:28 |
|
|




 3x+4y=(3k)4+4(2p)4=(32k-3k2p+1+22p+1)(32k+3k2p+1+22p+1) s mivel jobboldalt 5 hatványa van ezért mindkét tényező osztható kell legyen 5-el de ekkor az különbségük is osztható 5-el, az az 3k2p+2 osztható 5-el ami lehetetlen.
3x+4y=(3k)4+4(2p)4=(32k-3k2p+1+22p+1)(32k+3k2p+1+22p+1) s mivel jobboldalt 5 hatványa van ezért mindkét tényező osztható kell legyen 5-el de ekkor az különbségük is osztható 5-el, az az 3k2p+2 osztható 5-el ami lehetetlen. 

 h
h


 Q[X] polinomnak akkor
Q[X] polinomnak akkor  q
q