| [591] Sirpi | 2007-12-11 13:50:32 |
 Ügyes, tényleg fel lehet így írni :-) Ezt az "előjelezés nélküli determinánst" különben a mátrix permanensének hívják, és sajnos nem lehet polinomidőben kiszámítani.
|
| Előzmény: [590] nadorp, 2007-12-11 12:20:30 |
|
| [590] nadorp | 2007-12-11 12:20:30 |
 A feladat végülis egyszerű:-) Tekintsük az alábbi (n-1) X (n-1)-es táblázatot
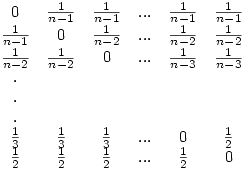
Ha most ezt úgy fejtjük,mint egy determinánst, de az összes negatív előjelet pluszra cseréljük, akkor éppen cn-et kapjuk.
|
| Előzmény: [589] Sirpi, 2007-12-11 10:21:51 |
|
| [589] Sirpi | 2007-12-11 10:21:51 |
 Köszi szépen, hogy utánanéztél. Én már az 5/36-odnál sejtettem, hogy ennek nem lesz szép és egyszerű megoldása, mint az eredetileg feldobott problémának volt az 1/e-vel.
|
| Előzmény: [587] nadorp, 2007-12-10 21:18:39 |
|
|
| [587] nadorp | 2007-12-10 21:18:39 |
 Szia Sirpi!
Ezt találtam, úgy néz ki elég nehéz:-(
Denominators of probabilities in gift exchange problem with n people.
A102263: n friends organize a gift exchange. The n names are put into a hat, and the first person draws one. If she picks her own name, then she returns it to the bag and draws again, repeating until she has a name that is not her own. Then the second person draws, again returning his own name if it is drawn. This continues down the line. What is the probability p(n) that when the n-th person draws, only her own name will be left in the bag?
A102263 I heard about the problem from Gary Thompson at Grove City College in PA.
A102263 As n increases, p(n) approaches 1/(n + log(n) + EulerGamma), where EulerGamma = .5772156649015... (the Euler-Mascheroni constant). - Jon E. Schoenfield (jonscho(AT)hiwaay.net), Sep 30 2006
A102263 See A102262 for formula for p(n).
A102263 p(2) through p(10) are 0, 1/4, 5/36, 19/144, 203/1800, 4343/43200, 63853/705600, 58129/705600, 160127/2116800.
A102263 Cf. A102262. A102263 Adjacent sequences: A102260 A102261 A102262 this sequence A102264 A102265 A102266
A102263 Sequence in context: A125756 A035287 A083223 this sequence A103931 A068589 A120077 A102263 nonn,frac A102263 2,2 A102263 Jerry Grossman (grossman(AT)oakland.edu), Feb 17 2005 A102263 More terms from Jon E. Schoenfield (jonscho(AT)hiwaay.net), Sep 30 2006
|
| Előzmény: [583] Sirpi, 2007-12-09 09:19:07 |
|
| [586] gortvalui | 2007-12-09 16:20:23 |
 2. A virágnektár 70százalék vizet tartalmaz és 17százalék méz készül belőle. Hány kg nektárt kell gyűjteni a méheknek 1kg mézhez?
3. A városi kutyapecér választásokon 5 jelölt indult. Semelyik két jelölt nem kapott ugyanannyi szavazatot, a győztesre 10-en szavaztak. Legfeljebb hány voksot gyűjthetett a legkutyaütőbb kutyapecérjejölt?
4. Ha a-(a-(a-(a-(a-1))))=1 akkor a=?
5. Egy étteremben egy főételért 2250ft-al többet kell fizetni,mint egy desszertért. A főétel és a desszert eggyütt 12x annyiba kerül mint a desszert. Mit mondhatunk a desszert áráról forintban?
6. Egy sakkmester szimultánt ad. Az első órában a befejezett játszmák 90százalékát nyeri meg, és 1partit veszít el. A szimultán befejezésekor a mester az első órában be nem fejezett játszmáknak csak a 20százalékát nyeri meg, 2partit elveszít és 2 parti döntetlenül végződik. Hány partit nem fejezett be az elsó órában?
7. Ha a 24009-et és a 41982-őt ugyanazzal a négyszámjegyű számmal elosztjuk, mindkétszer ugyanazt a maradékot kapjuk. Mi ez a maradék?
|
|
| [585] gortvalui | 2007-12-09 16:11:17 |
 Ezekben tudtok segíteni?
1. Krisztián 17g vízhez 3g sót kever! Hány százallékos sóoldatot kapott?
|
|
|
| [583] Sirpi | 2007-12-09 09:19:07 |
 Az 5/36 onnan jön, hogy összesen 2 kedvező eset van, viszont nem ugyanakkora a valószínűségük!
1234 -> 2314 és 1234 -> 3124 (itt egyszerűen az szerepel, hogy ki kit húz)
Az első eset valószínűsége: 1/3.1/3.1/2=2/36 (az egyes számok azt jelzik, hogy az 1-es, 2-es és 3-as milyen valószínűséggel húzza rendre a 2, 3, 1 cetliket)
A másodiké: 1/3.1/2.1/2=3/36. A különbséget az okozza, hogy ebben a 2. esetben miután az 1-es kihúzta a 3-ast, a kettes (mivel saját magát nem húzhatja), ezért csak 1 és 4 közül választhat, ezért különbözik a 2. szorzótényező. Remélem így már világos.
|
| Előzmény: [581] nadorp, 2007-12-08 22:57:11 |
|
|
| [581] nadorp | 2007-12-08 22:57:11 |
 Valószínű tényleg nem értem a példát :-( vagy nem látom a fától az erdőt.
Az 5/36 hogy jött ki, hiszen a 4 elemű permutációk száma csak 24, és 36>24. Ráadásul a kedvező esetek száma 2 (1->2->3->1) és (1->3->2->1), akkor miért van a számlábóban 5 ?
|
| Előzmény: [577] Sirpi, 2007-12-07 14:50:30 |
|
|
| [579] Róbert Gida | 2007-12-08 12:52:16 |
 A 3. feltételt elhagyhatod, pontosan akkor van ilyen pozitív egész számokból álló S halmazod, ha csak az 1,2,4 feltételek teljesülnek, többet nem tudok most mondani.
Legyen ugyanis T=S 2S 2S 3S 3S 6S, de a többszörös elemeket csak egyszer veszem bele. Legyen 6S, de a többszörös elemeket csak egyszer veszem bele. Legyen 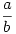 -nek egy előállítása: -nek egy előállítása:
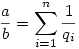
, ahol q1<q2<...<qn, ekkor

, ami az előzőtől különböző felbontás, így, ha S-ben legalább egy előállítás volt, akkor T-ben már legalább két különböző előállítás van.
|
| Előzmény: [578] SÁkos, 2007-12-08 11:30:45 |
|
| [578] SÁkos | 2007-12-08 11:30:45 |
 Van-e olyan valós számokat tartalmazó halmaz, amelynek elemeire a következő kitételek teljesülnek:
1) a halmaz elemei pozitív egész számok reciprokai
2) bármely ]0;1[ intervallumba eső racionális szám előáll a halmaz elemei közül véges soknak az összegeként úgy, hogy bármely elem legfeljebb egyszer szerepel ebben a felbontásban
3) bármely racionális számhoz végtelen sok különböző felbontás található (két felbontást különbözőnek tekintünk, ha van legalább 1 eltérő tag a felbontásban) például  esetén az esetén az 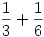 és és 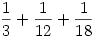 felbontásokat különbözőnek tekintjük. felbontásokat különbözőnek tekintjük.
4) a halmaz elemeinek összege véges
|
|
| [577] Sirpi | 2007-12-07 14:50:30 |
 Először a második kérdésedre válaszolnék:
Nem, an tényleg annak az esélyét jelöli, hogy az utolsó önmagát húzza. A rekurzió ugyanaz (lásd alább), de a kezdőérték nem: a0=0, a1=1, míg ha azt akarjuk kiszámolni, hogy az utolsó nem önmagát húzza, akkor a két értéket éppen fel kell cserélnünk.
A rekurzió: tegyük fel, hogy n-es indexig már kiszámoltuk az a sorozatot, és meg szeretnénk tudni an+1-et.
Az első húz, igazából teljesen szimmetrikus, hogy kit, tegyük fel ezért, hogy a 2-est. Most a 2-es vagy az 1-est húzza, vagy a 3...n+1 halmazból húz. Az első eset valószínűsége 1/n, és ilyenkor az a maradék n-1 gyerek tiszta lappal indul, annak valószínűsége, hogy az utolsó önmagát húzza, an-1. Ha a második eset következik be (valsége (n-1)/n), akkor vonjuk össze az 1-es és 2-es gyerekeket egy gyerekké. Így n gyerek marad, és kapjuk az (n-1)/n.an tagot.
* * *
És hogy mi a különbség a két feladat között? Elég sok, mert amit most feladtam, azt nem tudom megoldani :-)
Itt az a feladat, hogy ülésrend szerint sorban húznak, először az 1-es, aztán a 2-es, majd a 3-as, függetlenül attól, hogy ki kit húzott, és a kérdés a sorban n.-ről szól (jelöljük itt a valószínűséget cn-nel). Az előző feladatban a látott rekurzió alapján a0=0, a1=1, a2=0, a3=1/2, a4=1/3. Viszont az új feladatnál 3 gyerekre már nem 1/2 jön ki:
Az 1-es vagy a 2-est, vagy a 3-ast húzza. Utóbbi esetben a 3-as már nem fogja saját magát húzni, tehát csak az első eset az érdekes. Most a 2. húzhatja az 1-est, vagy a 3-ast, de megint csak az első eset az, amikor a 3-as végül saját magát húzza, így ilyenkor a valószínűség c3=1/2.1/2=1/4. Hasonlóan végig lehet gondolni, hogy c4=5/36 a4. a4.
|
| Előzmény: [576] nadorp, 2007-12-07 12:37:05 |
|
| [576] nadorp | 2007-12-07 12:37:05 |
 Bocsi, de lassulok. Mi a különbség az eredeti feladathoz képest ?
Másik kérdésem az lenne, hogy  nem annak a valószínűsége, hogy az utolsó NEM magát húzza ? nem annak a valószínűsége, hogy az utolsó NEM magát húzza ?
|
| Előzmény: [575] Sirpi, 2007-12-06 14:10:32 |
|
| [575] Sirpi | 2007-12-06 14:10:32 |
 Tökéletes, pont így csináltam én is :-)
Viszont valaki felvetette, hogy mi van, ha a körbeülés szerinti sorrendben húznak, függetlenül attól, hogy ki kit húzott ki (ilyenkor persze titokban is marad, hogy végül ki kinek ad ajándékot). Mit mondhatunk ilyenkor annak valószínűségéről, hogy az utolsó magát húzza? Annyit látok csak, hogy tart 0-hoz, de ezt leszámítva semmi értelmeset nem tudtam eddig mondani.
|
| Előzmény: [572] Cckek, 2007-12-06 13:14:49 |
|
|
|
|
| [571] Sirpi | 2007-12-06 12:58:06 |
 Na, akkor ott tartasz, ahol én egy órája :-) Tényleg ennyi a megoldás.
A feladat pedig, ami erre a rekurzióra vezet, a következő (elég aktuális is):
Van egy osztály, karácsonyi ajándékozásra készülvén körbeülnek, középen pedig ott egy kalap a neveikkel. Az első húz egyet, és ha nem magát húzta, akkor leül a helyére, és akit húzott, az jön következőnek. Ha valaki magát húzta, akkor újat húz (addig nem teszik vissza a cetlijét). Ha körbeér a dolog, akkor a legkisebb sorszámú, aki még nem húzott, megy oda következőnek a kalaphoz. Az utolsó embernél viszont probléma adódhat, lehet, hogy már csak a saját neve szerepel a kalapban, ilyenkor ugye nem tud újat húzni helyette, rossz a sorsolás. Az a kérdés, hogy mekkora ennek a valószínűsége.
|
| Előzmény: [570] rizsesz, 2007-12-06 12:10:33 |
|
| [570] rizsesz | 2007-12-06 12:10:33 |
 A miértje jó kérdés, de 1/e.
Biztos valami okos sorbafejtés. :)
|
|
| [569] Sirpi | 2007-12-06 11:57:53 |
 90. 0,301 91. 0,312 92. 0,301 93. 0,312 94. 0,302 95. 0,312 96. 0,302 97. 0,312 98. 0,302 99. 0,312 100. 0,302
Tehát szerinted a90=0,301, a91=0,312. Ekkor a92=90/91.0,312+1/91.0,301=0,31188
Szóval itt valamit elszámoltál (már a 90. tag se jó).
|
| Előzmény: [568] rizsesz, 2007-12-06 11:53:37 |
|
| [568] rizsesz | 2007-12-06 11:53:37 |
 Nekem az Excel ezt mondta:
90. 0,301 91. 0,312 92. 0,301 93. 0,312 94. 0,302 95. 0,312 96. 0,302 97. 0,312 98. 0,302 99. 0,312 100. 0,302
Szerintem a szomszédos elemek közötti különbség nem tart 0-hoz :(
|
| Előzmény: [567] Sirpi, 2007-12-06 11:40:44 |
|
| [567] Sirpi | 2007-12-06 11:40:44 |
 Nem tudom, volt-e már, de nekem egy feladat kapcsán a következő sorozat jött ki: a0=0, a1=1, majd a további indexekre:
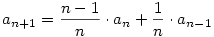
Ugye minden érték az előző kettő súlyozott számtani közepe, így a sorozat szűkülő intervallumokban oszcillál.
A feladat annak bizonyítása lenne, hogy ezeknek az [an,an+1] intervallumoknak 0-hoz tart a hossza, így a sorozatnak van határértéke, valamint mondjuk is meg, hogy mennyi.
Ha sikerült megoldanunk (nekem már igen :-) ), akkor elmondom majd azt is, hogy mi volt a feladat :-)
|
|





 2S
2S
 a4.
a4.
 x1=1, ekkor
x1=1, ekkor